Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Keller, Gerhard
and
Nowicki, Tomasz
1992.
Spectral theory, zeta functions and the distribution of periodic points for Collet-Eckmann maps.
Communications in Mathematical Physics,
Vol. 149,
Issue. 1,
p.
31.
Sharkovsky, A.N.
and
Chua, L.O.
1993.
Chaos in some 1-D discontinuous maps that appear in the analysis of electrical circuits.
IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,
Vol. 40,
Issue. 10,
p.
722.
Keller, Gerhard
1994.
Exponential weak Bernoulli mixing for collet-eckmann maps.
Israel Journal of Mathematics,
Vol. 86,
Issue. 1-3,
p.
301.
Bruin, H.
1994.
Topological conditions for the existence of invariant measures for unimodal maps.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
433.
Martens, Marco
1994.
Distortion results and invariant Cantor sets of unimodal maps.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 2,
p.
331.
Jakobson, Michael
and
Światek, Grzegorz
1994.
Metric properties of non-renormalizableS-unimodal maps. Part I: Induced expansion and invariant measures.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 4,
p.
721.
Blokh, Alexander M.
1995.
Dynamics Reported.
Vol. 4,
Issue. ,
p.
1.
Keller, Gerhard
and
Nowicki, Tomasz
1995.
Fibonacci maps re(aℓ)visited.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 1,
p.
99.
Pollicott, Mark
1995.
One-dimensional maps via complex analysis in several variables.
Israel Journal of Mathematics,
Vol. 91,
Issue. 1-3,
p.
317.
Vargas, E.
1996.
Measure of minimal sets of polymodal maps.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 1,
p.
159.
Buzzi, J�r�me
1997.
Intrinsic ergodicity of affine maps in [0, 1] d.
Monatshefte f�r Mathematik,
Vol. 124,
Issue. 2,
p.
97.
Nowicki, Tomasz
1998.
European Congress of Mathematics.
p.
116.
Bruin, Henk
and
Hawkins, Jane
1998.
Examples of expandingC 1 maps having no σ-finite invariant measure equivalent to Lebesgue.
Israel Journal of Mathematics,
Vol. 108,
Issue. 1,
p.
83.
Alves, José F.
Bonatti, Christian
and
Viana, Marcelo
2000.
The Theory of Chaotic Attractors.
p.
443.
Yuan, Guocheng
and
Yorke, James A.
2000.
Collapsing of chaos in one dimensional maps.
Physica D: Nonlinear Phenomena,
Vol. 136,
Issue. 1-2,
p.
18.
Keller, Gerhard
and
Pierre, Matthias St.
2001.
Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems.
p.
333.
Thunberg, Hans
2001.
Periodicity versus Chaos in One-Dimensional Dynamics.
SIAM Review,
Vol. 43,
Issue. 1,
p.
3.
Jakobson, M.
and
Świątek, G.
2002.
Vol. 1,
Issue. ,
p.
599.
AARONSON, J.
DENKER, M.
SARIG, O.
and
ZWEIMÜLLER, R.
2004.
APERIODICITY OF COCYCLES AND CONDITIONAL LOCAL LIMIT THEOREMS.
Stochastics and Dynamics,
Vol. 04,
Issue. 01,
p.
31.
de Melo, Welington
2004.
Bifurcation of unimodal maps.
Qualitative Theory of Dynamical Systems,
Vol. 4,
Issue. 2,
p.
413.
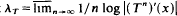 for Lebesgue-a.e. x.
for Lebesgue-a.e. x.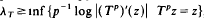 , i.e. uniform hyperbolicity on periodic points implies λT > 0, and λT < 0 implies the existence of a stable periodic orbit.
, i.e. uniform hyperbolicity on periodic points implies λT > 0, and λT < 0 implies the existence of a stable periodic orbit.



