Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T12:09:40.125Z Has data issue: false hasContentIssue false
  • English
  • Français

The escaping set of transcendental self-maps of the punctured plane

Published online by Cambridge University Press:  13 October 2016

DAVID MARTÍ-PETE
DAVID MARTÍ-PETE*
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK email david.martipete@open.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the different rates of escape of points under iteration by holomorphic self-maps of 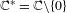$\mathbb{C}^{\ast }=\mathbb{C}\setminus \{0\}$ for which both zero and infinity are essential singularities. Using annular covering lemmas we construct different types of orbits, including fast escaping and arbitrarily slowly escaping orbits to either zero, infinity or both. We also prove several properties about the set of fast escaping points for this class of functions. In particular, we show that there is an uncountable collection of disjoint sets of fast escaping points, each of which has 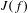$J(f)$ as its boundary.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 739 - 760
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlfors, L. V.. Complex Aanalysis. An Introduction to the Theory of Analytic Functions of One Complex Variable. McGraw-Hill, New York–Toronto–London, 1953.Google Scholar
Baker, I. N.. Wandering domains for maps of the punctured plane. Ann. Acad. Sci. Fenn. Math. Ser. A I Math. 12(2) (1987), 191–198.CrossRefGoogle Scholar
Baker, I. N.. Infinite limits in the iteration of entire functions. Ergod. Th. & Dynam. Sys. 8(4) (1988), 503–507.CrossRefGoogle Scholar
Baker, I. N. and Domínguez-Soto, P.. Analytic self-maps of the punctured plane. Complex Var. Theory Appl. 37(1–4) (1998), 67–91.Google Scholar
Baker, I. N., Domínguez-Soto, P. and Herring, M. E.. Dynamics of functions meromorphic outside a small set. Ergod. Th. & Dynam. Sys. 21(3) (2001), 647–672.CrossRefGoogle Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N.S.) 29(2) (1993), 151–188.CrossRefGoogle Scholar
Bergweiler, W.. On the Julia set of analytic self-maps of the punctured plane. Analysis 15(3) (1995), 251–256.CrossRefGoogle Scholar
Bergweiler, W. and Hinkkanen, A.. On semiconjugation of entire functions. Math. Proc. Cambridge Philos. Soc. 126(3) (1999), 565–574.CrossRefGoogle Scholar
Bhattacharyya, P.. Iteration of analytic functions. PhD thesis, University of London, 1969.Google Scholar
Beardon, A. F. and Minda, D.. The hyperbolic metric and geometric function theory, Quasiconformal Mappings and Their Applications, Narosa, New Delhi, 2007, pp. 9–56.Google Scholar
Bergweiler, W., Rippon, P. J. and Stallard, G. M.. Multiply connected wandering domains of entire functions. Proc. Lond. Math. Soc. (3) 107(6) (2013), 1261–1301.CrossRefGoogle Scholar
Eremenko, A. E.. On the iteration of entire functions. Dynamical Systems and Ergodic Theory (Warsaw 1986) (Banach Center Publications, 23) . PWN, Warsaw, 1989, pp. 339–345.Google Scholar
Eremenko, A. E. and Lyubich, M. Yu.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42(4) (1992), 989–1020.CrossRefGoogle Scholar
Fagella, N.. Dynamics of the complex standard family. J. Math. Anal. Appl. 229(1) (1999), 1–31.CrossRefGoogle Scholar
Fang, L.. Complex dynamical systems on C ∗ . Acta Math. Sinica 34(5) (1991), 611–621.Google Scholar
Fang, L.. Area of Julia sets of holomorphic self-maps on C ∗ . Acta Math. Sinica (N.S.) 9(2) (1993), 160–165. A Chinese summary appears in Acta Math. Sinica 37(3) (1994), 431.Google Scholar
Fang, L.. Completely invariant domains of holomorphic self-maps on C ∗ . J. Beijing Inst. Technol. 6(3) (1997), 187–191.Google Scholar
Fang, L.. On the iteration of holomorphic self-maps of C ∗ . Acta Math. Sinica (N.S.) 14(1) (1998), 139–144.Google Scholar
Fatou, P.. Sur l’itération des fonctions transcendantes entières. Acta Math. 47(4) (1926), 337–370.CrossRefGoogle Scholar
Fagella, N. and Martí-Pete, D.. Dynamic rays of bounded-type transcendental self-maps of the punctured plane. Discrete Contin. Dyn. Syst., to appear. Preprint, 2016, arXiv:1603.03311.Google Scholar
Hinkkanen, A.. Completely invariant components in the punctured plane. New Zealand J. Math. 23(1) (1994), 65–69.Google Scholar
Keen, L.. Dynamics of holomorphic self-maps of C ∗ . Holomorphic Functions and Moduli, Vol. I (Mathematical Sciences Research Institute Publications, 10) . Springer, New York, 1988, pp. 9–30.CrossRefGoogle Scholar
Keen, L.. Topology and growth of a special class of holomorphic self-maps of C ∗ . Ergod. Th. & Dynam. Sys. 9(2) (1989), 321–328.CrossRefGoogle Scholar
Kotus, J.. Iterated holomorphic maps on the punctured plane. Dynamical Systems (Sopron 1985) (Lecture Notes in Economics and Mathematical Systems, 287) . Springer, Berlin, 1987, pp. 10–28.CrossRefGoogle Scholar
Kotus, J.. The domains of normality of holomorphic self-maps of C ∗ . Ann. Acad. Sci. Fenn. Math. Ser. A I Math. 15(2) (1990), 329–340.CrossRefGoogle Scholar
Makienko, P. M.. Iterations of analytic functions in C ∗ . Dokl. Akad. Nauk SSSR 297(1) (1987), 35–37.Google Scholar
Makienko, P. M.. Herman rings in the theory of iterations of endomorphisms of C ∗ . Sibirsk. Mat. Zh. 32(3) (1991), 97–103.Google Scholar
Milnor, J. W.. Dynamics in one complex variable (Annals of Mathematics Studies, 160) , 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Mukhamedshin, A. N.. Mapping of a punctured plane with wandering domains. Sibirsk. Mat. Zh. 32(2) (1991), 184–187, 214.Google Scholar
Newman, M. H. A.. Elements of the Topology of Plane Sets of Points, 2nd edn. Cambridge University Press, New York, 1961.Google Scholar
Rådström, H.. On the iteration of analytic functions. Math. Scand. 1 (1953), 85–92.CrossRefGoogle Scholar
Rottenfusser, G., Rückert, J., Rempe, L. and Schleicher, D.. Dynamic rays of bounded-type entire functions. Ann. of Math. (2) 173(1) (2011), 77–125.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. On the sets where iterates of a meromorphic fucntion zip towards infinity. Bull. Lond. Math. Soc. 32(5) (2000), 528–536.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. On questions of Fatou and Eremenko. Proc. Amer. Math. Soc. 133(4) (2005), 1119–1126.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. Functions of small growth with no unbounded Fatou components. J. Anal. Math. 108 (2009), 61–86.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. Fast escaping points of entire functions. Proc. Lond. Math. Soc. (3) 105(4) (2012), 787–820.CrossRefGoogle Scholar
Rippon, P. J. and Stallard, G. M.. Annular itineraries for entire functions. Trans. Amer. Math. Soc. 367(1) (2015), 377–399.CrossRefGoogle Scholar