Hostname: page-component-7479d7b7d-jwnkl Total loading time: 0 Render date: 2024-07-11T14:23:54.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding topological dynamical systems with periodic points in cubical shifts

Published online by Cambridge University Press:  22 July 2015

YONATAN GUTMAN
YONATAN GUTMAN*
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-956 Warszawa, Poland email y.gutman@impan.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

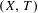According to a conjecture of Lindenstrauss and Tsukamoto, a topological dynamical system $(X,T)$ is embeddable in the 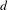$d$-cubical shift 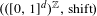$(([0,1]^{d})^{\mathbb{Z}},\text{shift})$ if both its mean dimension and periodic dimension are strictly bounded by 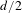$d/2$. We verify the conjecture for the class of systems admitting a finite-dimensional non-wandering set and a closed set of periodic points. This class of systems is closely related to systems arising in physics. In particular, we prove an embedding theorem for systems associated with the two-dimensional Navier–Stokes equations of fluid mechanics. The main tool in the proof of the embedding result is the new concept of local markers. Continuing the investigation of (global) markers initiated in previous work it is shown that the marker property is equivalent to a topological version of the Rokhlin lemma. Moreover, new classes of systems are found to have the marker property, in particular, extensions of aperiodic systems with a countable number of minimal subsystems. Extending work of Lindenstrauss we show that, for systems with the marker property, vanishing mean dimension is equivalent to the small boundary property.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 2 , April 2017 , pp. 512 - 538
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematics Studies, 153) . North-Holland Publishing Co., Amsterdam, 1988, p. 122; Notas de Matemática [Mathematical Notes].Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
Downarowicz, T.. Entropy of a symbolic extension of a dynamical system. Ergod. Th. & Dynam. Sys. 21(4) (2001), 1051–1070.CrossRefGoogle Scholar
Downarowicz, T.. Minimal models for noninvertible and not uniquely ergodic systems. Israel J. Math. 156 (2006), 93–110.CrossRefGoogle Scholar
Dugundji, J.. Topology. Allyn and Bacon Inc., Boston, MA, 1966.Google Scholar
Foias, C., Manley, O., Rosa, R. and Temam, R.. Navier–Stokes Equations and Turbulence (Encyclopedia of Mathematics and its Applications, 83) . Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Gromov, M.. Topological invariants of dynamical systems and spaces of holomorphic maps. I. Math. Phys. Anal. Geom. 2(4) (1999), 323–415.CrossRefGoogle Scholar
Gutman, Y. and Tsukamoto, M.. Mean dimension and a sharp embedding theorem: extensions of aperiodic subshifts. Ergod. Th. & Dynam. Sys. 34 (2014), 1888–1896.CrossRefGoogle Scholar
Gutman, Y.. Embedding ℤ k -actions in cubical shifts and ℤ k -symbolic extensions. Ergod. Th. & Dynam. Sys. 31(2) (2011), 383–403.CrossRefGoogle Scholar
Gutman, Y.. Mean dimension and Jaworski-type theorems. Preprint, 2012, arXiv:1208.5248.Google Scholar
Gutman, Y.. Dynamical embedding in cubical shifts and the topological Rokhlin and small boundary properties. Preprint, 2013, arXiv:1301.6072.Google Scholar
Hale, J. K.. Asymptotic Behavior of Dissipative Systems (Mathematical Surveys and Monographs, 25) . American Mathematical Society, Providence, RI, 1988.Google Scholar
Jaworski, A.. The Kakutani–Beboutov theorem for groups. PhD Dissertation, University of Maryland, 1974.Google Scholar
Krieger, W.. On the subsystems of topological Markov chains. Ergod. Th. & Dynam. Sys. 2(2) (1982), 195–202.CrossRefGoogle Scholar
Kukavica, I.. An absence of a certain class of periodic solutions in the Navier–Stokes equations. J. Dynam. Differential Equations 6(1) (1994), 175–183.CrossRefGoogle Scholar
Ladyzhenskaya, O.. Attractors for Semigroups and Evolution Equations (Lezioni Lincee. [Lincei Lectures]) . Cambridge University Press, Cambridge, 1991.CrossRefGoogle Scholar
Lindenstrauss, E.. Mean dimension, small entropy factors and an embedding theorem. Publ. Math. Inst. Hautes Études Sci. 89(1) (1999), 227–262.CrossRefGoogle Scholar
Lindenstrauss, E. and Tsukamoto, M.. Mean dimension and an embedding problem: an example. Israel J. Math. 199 (2014), 573–584.CrossRefGoogle Scholar
Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.CrossRefGoogle Scholar
Robinson, J. C.. Dimensions, Embeddings, and Attractors (Cambridge Tracts in Mathematics, 186) . Cambridge University Press, Cambridge, 2011.Google Scholar
Robinson, J. C.. Attractors and finite-dimensional behaviour in the 2D Navier–Stokes equations. ISRN Math. Anal. (2013), Article 291823, 29.CrossRefGoogle Scholar
Shub, M. and Weiss, B.. Can one always lower topological entropy? Ergod. Th. & Dynam. Sys. 11(3) (1991), 535–546.CrossRefGoogle Scholar
Temam, R.. Some properties of functional invariant sets for Navier–Stokes equations. Bifurcation Phenomena in Mathematical Physics and Related Topics. Proc. NATO Advanced Study Institute, Cargèse, 1979 (NATO Advanced Study Institute Series C: Mathematical and Physical Sciences, 54) . Reidel, Dordrecht, 1980, pp. 551–554.Google Scholar
Temam, R.. Infinite-dimensional Dynamical Systems in Mechanics and Physics (Applied Mathematical Sciences, 68) , 2nd edn. Springer, New York, 1997.CrossRefGoogle Scholar
Tsukamoto, M.. Moduli space of Brody curves, energy and mean dimension. Nagoya Math. J. 192 (2008), 27–58.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.CrossRefGoogle Scholar