Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T08:36:08.963Z Has data issue: false hasContentIssue false
  • English
  • Français

A dynamical approach to the asymptotic behavior of the sequence 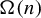$\Omega (n)$

Part of: Ergodic theory Multiplicative number theory

Published online by Cambridge University Press:  29 November 2022

KAITLYN LOYD Open the ORCID record for KAITLYN LOYD [Opens in a new window]
KAITLYN LOYD*
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208, USA
*
e-mail: loydka@math.northwestern.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the asymptotic behavior of the sequence 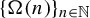$ \{\Omega (n) \}_{ n \in \mathbb {N} } $ from a dynamical point of view, where 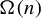$ \Omega (n) $ denotes the number of prime factors of $ n $ counted with multiplicity. First, we show that for any non-atomic ergodic system 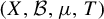$(X, \mathcal {B}, \mu , T)$, the operators 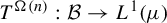$T^{\Omega (n)}: \mathcal {B} \to L^1(\mu )$ have the strong sweeping-out property. In particular, this implies that the pointwise ergodic theorem does not hold along 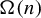$\Omega (n)$. Second, we show that the behaviors of 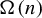$\Omega (n)$ captured by the prime number theorem and Erdős–Kac theorem are disjoint, in the sense that their dynamical correlations tend to zero.

Keywords

classical ergodic theoryergodic theoremsnumber theoryprime number theorem

MSC classification

Secondary: 37A30: Ergodic theorems, spectral theory, Markov operators 11N37: Asymptotic results on arithmetic functions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 11 , November 2023 , pp. 3685 - 3706
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V. and Richter, F. K.. Dynamical generalizations of the prime number theorem and disjointness of additive and multiplicative semigroup actions. Duke Math. J. 171(15) (2022), 3133–3200.CrossRefGoogle Scholar
Delange, H.. On some arithmetical functions. Illinois J. Math. 2(1) (1958), 81–87.CrossRefGoogle Scholar
Erdos, P. and Kac, M.. The Gaussian law of errors in the theory of additive number theoretic functions. Amer. J. Math. 62(1) (1940), 738–742.10.2307/2371483CrossRefGoogle Scholar
Erdős, P.. On the distribution function of additive functions. Ann. of Math. (2) 47(1) (1946), 1–20.10.2307/1969031CrossRefGoogle Scholar
Erdős, P.. On the integers having exactly K prime factors. Ann. of Math. (2) 49(1) (1948), 53–66.10.2307/1969113CrossRefGoogle Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 259). Springer, London, 2011.10.1007/978-0-85729-021-2CrossRefGoogle Scholar
Host, B. and Kra, B.. Uniformity seminorms on ${\ell}^{\infty }$ and applications. J. Anal. Math. 108(1) (2009), 219–276.10.1007/s11854-009-0024-1CrossRefGoogle Scholar
Hardy, G. H. and Ramanujan, S.. The normal number of prime factors of a number $n$ . Q. J. Pure Appl. Math. 48 (1917), 76–92.Google Scholar
Landau, E.. Handbuch der Lehre von der Verteilung der Primzahlen, 2nd edn. Vol. 2. Chelsea Publishing Co., New York, 1953.Google Scholar
Pillai, S. S.. Generalisation of a theorem of Mangoldt. Proc. Indian Acad. Sci. – Sect. A 11(1) (1940), 13–20.CrossRefGoogle Scholar
Richter, F. K.. A new elementary proof of the prime number theorem. Bull. Lond. Math. Soc. 53(5) (2021), 1365–1375.10.1112/blms.12503CrossRefGoogle Scholar
Rosenblatt, J. M. and Wierdl, M.. Pointwise ergodic theorems via harmonic analysis. Ergodic Theory and its Connections with Harmonic Analysis: Proceedings of the 1993 Alexandria Conference. Eds. Peterson, K. E. and Salama, I.. Cambridge University Press, Cambridge, 1994, pp. 3–152.Google Scholar
Selberg, S.. Zur Theorie der quadratfreien Zahlen. Math. Z. 44(1) (1939), 306–318.CrossRefGoogle Scholar
von Mangoldt, H. C. F.. Beweis der gleichung ${\sum}_{k=1}^{\infty}\frac{\mu (k)}{k}=0$ . Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Zweiter Halbband – Juli bis Dezember 1897, pp. 835–852, https://biodiversitylibrary.org/page/29982413.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer-Verlag, New York, 1982.CrossRefGoogle Scholar
Weyl, H.. Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77(3) (1916), 313–352.CrossRefGoogle Scholar