Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-22T23:22:13.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Directional recurrence and directional rigidity for infinite measure preserving actions of nilpotent lattices

Published online by Cambridge University Press:  11 February 2016

ALEXANDRE I. DANILENKO
ALEXANDRE I. DANILENKO*
Affiliation:
Institute for Low Temperature Physics & Engineering of National Academy of Sciences of Ukraine, 47 Lenin Avenue, Kharkov61164, Ukraine email alexandre.danilenko@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 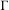$\unicode[STIX]{x1D6E4}$ be a lattice in a simply connected nilpotent Lie group 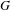$G$. Given an infinite measure-preserving action $T$ of 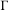$\unicode[STIX]{x1D6E4}$ and a ‘direction’ in 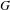$G$ (i.e. an element $\unicode[STIX]{x1D703}$ of the projective space 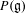$P(\mathfrak{g})$ of the Lie algebra $\mathfrak{g}$ of 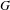$G$), some notions of recurrence and rigidity for $T$ along $\unicode[STIX]{x1D703}$ are introduced. It is shown that the set of recurrent directions 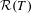${\mathcal{R}}(T)$ and the set of rigid directions for $T$ are both 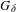$G_{\unicode[STIX]{x1D6FF}}$. In the case where 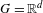$G=\mathbb{R}^{d}$ and 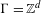$\unicode[STIX]{x1D6E4}=\mathbb{Z}^{d}$, we prove that (a) for each 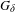$G_{\unicode[STIX]{x1D6FF}}$-subset 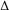$\unicode[STIX]{x1D6E5}$ of 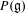$P(\mathfrak{g})$ and a countable subset 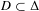$D\subset \unicode[STIX]{x1D6E5}$, there is a rank-one action $T$ such that 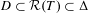$D\subset {\mathcal{R}}(T)\subset \unicode[STIX]{x1D6E5}$ and (b) 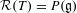${\mathcal{R}}(T)=P(\mathfrak{g})$ for a generic infinite measure-preserving action $T$ of 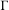$\unicode[STIX]{x1D6E4}$. This partly answers a question from a recent paper by Johnson and Şahin. Some applications to the directional entropy of Poisson actions are discussed. In the case where 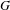$G$ is the Heisenberg group 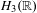$H_{3}(\mathbb{R})$ and 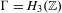$\unicode[STIX]{x1D6E4}=H_{3}(\mathbb{Z})$, a rank-one 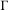$\unicode[STIX]{x1D6E4}$-action $T$ is constructed for which 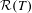${\mathcal{R}}(T)$ is not invariant under the natural ‘adjoint’ 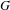$G$-action.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 6 , September 2017 , pp. 1841 - 1861
Copyright
© Cambridge University Press, 2016 

References

Aaronson, J.. Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50) . American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Adams, T. M. and Silva, C. E.. On infinite transformations with maximal control of ergodic two-fold product powers. Israel J. Math. 209 (2015), 929–948.CrossRefGoogle Scholar
Auslander, L., Green, L. W. and Hahn, F.. Flows on Homogeneous Spaces. Princeton University Press, Princeton, NJ, 1963.CrossRefGoogle Scholar
Danilenko, A. I.. (C, F)-Actions in Ergodic Theory (Progress in Mathematics, 265) . Birkhäuser, Basel, 2008, pp. 325–351.Google Scholar
Danilenko, A. I.. Actions of finite rank: weak rational ergodicity and partial rigidity. Ergod. Th. & Dynam. Sys., to appear.Google Scholar
Danilenko, A. I. and Lemańczyk, M.. Odometer actions of the Heisenberg group. J. Anal. Math., to appear.Google Scholar
Danilenko, A. I. and Silva, C. E.. Ergodic Theory: Nonsingular Transformations (Encyclopedia of Complexity and Systems Science) . Springer, New York, 2009, pp. 3055–3083.Google Scholar
Feldman, J.. A ratio ergodic theorem for commuting, conservative, invertible transformations with quasi-invariant measure summed over symmetric hypercubes. Ergod. Th. & Dynam. Sys. 27 (2007), 1135–1142.CrossRefGoogle Scholar
Ferenczi, S. and Kamiński, B.. Zero entropy and directional Bernoullicity of a Gaussian ℤ2 -action. Proc. Amer. Math. Soc. 123 (1995), 3079–3083.Google Scholar
Janvresse, E., Meyerovitch, T., Roy, E. and de la Rue, T.. Poisson suspensions and entropy for infinite transformations. Trans. Amer. Math. Soc. 362 (2010), 3069–3094.CrossRefGoogle Scholar
Johnson, A. S. A. and Şahin, A. A.. Directional recurrence for infinite measure preserving ℤ d -actions. Ergod. Th. & Dynam. Sys. 35 (2015), 2138–2150.CrossRefGoogle Scholar
Mackey, G.. Induced representations of locally compact groups. I. Ann. of Math. (2) 55 (1952), 101–139.CrossRefGoogle Scholar
Malcev, A. I.. On a class of homogeneous spaces. Izv. Akad. Nauk. SSSR Ser. Mat. 13 (1949), 9–32 (in Russian).Google Scholar
Milnor, J.. On the entropy geometry of cellular automata. Complex Systems 2 (1988), 357–385.Google Scholar
Neretin, Y.. Categories of Symmetries and Infinite-Dimensional Groups (London Mathematical Society Monographs. New Series, 16) . Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1996.CrossRefGoogle Scholar
Park, K. K.. On directional entropy functions. Israel J. Math. 113 (1999), 243–267.CrossRefGoogle Scholar
Roy, E.. Poisson suspensions and infinite ergodic theory. Ergod. Th. & Dynam. Sys. 29 (2009), 667–683.CrossRefGoogle Scholar
Zimmer, R. J.. Induced and amenable ergodic actions of Lie groups. Ann. Sci. Éc. Norm. Supér. 11 (1978), 407–428.CrossRefGoogle Scholar