Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-25T02:17:51.756Z Has data issue: false hasContentIssue false
  • English
  • Français

Differentiation of SRB states for hyperbolic flows

Published online by Cambridge University Press:  01 April 2008

DAVID RUELLE
DAVID RUELLE*
Affiliation:
Mathematics Department, Rutgers University, and IHES, 91440 Bures sur Yvette, France (email: ruelle@ihes.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

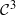Let the vector field 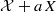on M define a flow (fat) with an Axiom A attractor Λa depending continuously on a∈(−ϵ,ϵ). Let ρa be the SRB measure on Λa for (fat). If 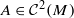, then 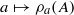is 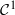on (−ϵ,ϵ) and dρa(A)/da is the limit when ω→0 with Im ω>0 of

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 613 - 631
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Anosov, D. V.. Geodesic flows on compact Riemann manifolds of negative curvature. Proc. Steklov Inst. Math. 90 (1967), 1–209.Google Scholar
[2]Bakhtin, V. I.. Random processes generated by a hyperbolic sequence of mappings. I. Russian Acad. Sci. Izv. Math. 44 (1995), 247–279.Google Scholar
[3]Bonatti, C., Diaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Approach (Encyclopaedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
[4]Bowen, R.. Markov partitions for Axiom A diffeomorphisms. Amer. J. Math. 92 (1970), 725–747.CrossRefGoogle Scholar
[5]Bowen, R.. Periodic orbits for hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.CrossRefGoogle Scholar
[6]Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
[7]Bowen, R.. On Axiom A Diffeomorphisms (CBMS Regional Conference, 35). American Mathetical Society, Providence, RI, 1978.Google Scholar
[8]Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.CrossRefGoogle Scholar
[9]Chernov, N.. Markov approximations and decay of correlations for Anosov flows. Ann. of Math. 147 (1998), 269–324.CrossRefGoogle Scholar
[10]Contreras, G.. Regularity of topological and metric entropy of hyperbolic flows. Math. Z. 210 (1992), 97–111.CrossRefGoogle Scholar
[11]Contreras, G.. The derivatives of equilibrium states. Bol. Soc. Brasil. Mat. (N.S.) 26 (1995), 211–228.CrossRefGoogle Scholar
[12]Dolgopyat, D.. Decay of correlations in Anosov flows. Ann. of Math. 147 (1998), 357–390.CrossRefGoogle Scholar
[13]Dolgopyat, D.. Prevalence of rapid mixing in hyperbolic flows. Ergod. Th. & Dynam. Sys. 18 (1998), 1097–1114. Prevalence of rapid mixing-II: topological prevalence. Ergod. Th. & Dynam. Sys. 20 (2000), 1045–1059.CrossRefGoogle Scholar
[14]Dolgopyat, D.. On differentiability of SRB states for partially hyperbolic systems. Invent. Math. 155 (2004), 389–449.CrossRefGoogle Scholar
[15]Field, M., Melbourne, I. and Török, A.. Stability of mixing for hyperbolic flows. Ann. of Math. To appear.Google Scholar
[16]Gallavotti, G. and Cohen, E. G. D.. Dynamical ensembles in stationary states. J. Stat. Phys. 80 (1995), 931–970.CrossRefGoogle Scholar
[17]Katok, A., Knieper, G., Pollicott, M. and Weiss, H.. Differentiability and analyticity of topological entropy for Anosov and geodesic flows. Invent. Math. 98 (1989), 581–597.CrossRefGoogle Scholar
[18]Ledrappier, F. and Strelcyn, J.-M.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2 (1982), 203–219.CrossRefGoogle Scholar
[19]Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: I. Characterization of measures satisfying Pesin’s formula. II. Relations between entropy, exponents and dimension. Ann. of Math. 122 (1985), 509–539, 540–574.Google Scholar
[20]Liverani, C.. On contact Anosov flows. Ann. of Math. 159 (2004), 1275–1312.CrossRefGoogle Scholar
[21]de la Llave, R., Marco, J. M. and Moriyon, R.. Canonical perturbation theory of Anosov systems and regularity results for the Livsic cohomology equation. Ann. of Math. 123 (1986), 537–611.CrossRefGoogle Scholar
[22]Pollicott, M.. On the rate of mixing of Axiom A flows. Invent. Math. 81 (1982), 423–426.Google Scholar
[23]Ratner, M.. Markov partitions for Anosov flows on 3-dimensional manifolds. Mat. Zametki 6 (1969), 693–704.Google Scholar
[24]Ruelle, D.. A measure associated with Axiom A attractors. Amer. J. Math. 98 (1976), 619–654.CrossRefGoogle Scholar
[25]Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, Reading, MA, 1978.Google Scholar
[26]Ruelle, D.. Resonances for Axiom A flows. J. Differential Geom. 25 (1987), 99–116.CrossRefGoogle Scholar
[27]Ruelle, D.. I. Differentiation of SRB states; II. Correction and complements. Comm. Math. Phys. 187 (1997), 227–241; 234 (2003), 185–190.CrossRefGoogle Scholar
[28]Ruelle, D.. Smooth dynamics and new theoretical ideas in nonequilibrium statistical mechanics. J. Stat. Phys. 95 (1999), 393–468.CrossRefGoogle Scholar
[29]Sinai, Ya. G.. Markov partitions and C-diffeomorphisms. Funktsional. Anal. i Prilozhen 2(1) (1968), 64–89. (Engl. Transl. Funct. Anal. Appl. 2 (1968), 61–82).CrossRefGoogle Scholar
[30]Sinai, Ya. G.. Constuction of Markov partitions. Funktsional. Anal. i Prilozhen 2(3) (1968), 70–80. (Engl. Transl. Funct. Anal. Appl. 2 (1968), 245–253).CrossRefGoogle Scholar
[31]Sinai, Ya. G.. Gibbsian measures in ergodic theory. Uspekhi Mat. Nauk 27(4) (1972), 21–64. English translation, Russian Math. Surveys 27(4) (1972), 21–69.Google Scholar
[32]Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
[33]Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. 147 (1998), 585–650.CrossRefGoogle Scholar
[34]Butterley, O. and Liverani, C.. Smooth Anosov flows: correlation spectra and stability. J. Mod. Dynam. 1 (2007), 301–322.CrossRefGoogle Scholar
[35]Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990).Google Scholar