Article contents
A construction of subshifts and a class of semigroups
Published online by Cambridge University Press: 22 January 2020
Abstract
Subshifts with property 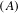 $(A)$ are constructed from a class of directed graphs. As special cases the Markov–Dyck shifts are shown to have property
$(A)$ are constructed from a class of directed graphs. As special cases the Markov–Dyck shifts are shown to have property 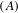 $(A)$. The semigroups that are associated to
$(A)$. The semigroups that are associated to 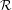 ${\mathcal{R}}$-graph shifts with Property
${\mathcal{R}}$-graph shifts with Property 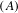 $(A)$ are determined.
$(A)$ are determined.
MSC classification
- Type
- Original Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2020
References
- 2
- Cited by





