Hostname: page-component-7479d7b7d-fwgfc Total loading time: 0 Render date: 2024-07-12T19:22:47.838Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of C∞-stable foliations

Published online by Cambridge University Press:  19 September 2008

Aziz El Kacimi Alaoui  and
Marcel Nicolau
Aziz El Kacimi Alaoui
Affiliation:
URA au CNRS 751, Université de Valenciennes, 59326 Valenciennes Cedex, France
Marcel Nicolau
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider foliations F obtained as the suspension of a linear foliation F0 on 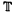n by means of a linear Anosov diffeomorphism A of 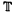n keeping F0 invariant. Under suitable conditions on A the foliations F are shown to be C∞-stable, i.e. any differentiable foliation which is C∞-close to F is C∞-conjugated to F. The proof relies on a criterium of stability stated by R. Hamilton.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 13 , Issue 4 , December 1993 , pp. 697 - 704
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B-L]Benoist, Y. & Labourie, F.. Sur les diffeomorphismes d'Anosov a feuilletages stable et instable differentiables. Preprint. Ecole Polytechnique No. 1033 (1992).Google Scholar
[G1]Ghys, E.. Actions localement libres du groups affine. Invent. Math. 82 (1985), 479–526.CrossRefGoogle Scholar
[G2]Ghys, E.. Rots d' Anosov dont les feuilletages stables sont difflrentiables. Ann. Sci. Éc. Norm. Sup. 20 (1987), 251–270.CrossRefGoogle Scholar
[G-S]Ghys, E. & Sergiescu, V.. Stabilité et conjugaison différentiable pour certains feuilletages. Topology 19 (1980), 179–197.CrossRefGoogle Scholar
[Has]Hasselblatt, B.. Regularity of the Anosov splitting and of horospheric foliations. Preprint. IHES (1991).Google Scholar
[Ham1]Hamilton, R.. Deformation theory of foliations. Preprint. Cornell University, New York (1978).Google Scholar
[Ham2]Hamilton, R.. The implicit function theorem of Nash and Moser. Bull. Amer. Math. Soc. 7 (1982), 65–222.CrossRefGoogle Scholar
[Hu1]Hurder, S.. Deformation rigidity for subgroups of SL(n, Z) acting on the n-torus. Bull. Amer. Math. Soc. 23 (1990), 107–113.CrossRefGoogle Scholar
[Hu2]Hurder, S.. Rigidity for Anosov actions of higher rank lattices. Ann. Math. 135 (1992), 361–410.CrossRefGoogle Scholar
[H-K]Hurder, S. & Katok, A.. Differentiability, rigidity and Godbillon—Vey classes for Anosov foliations. Publ. Math. IHES 72 (1990), 5–61.CrossRefGoogle Scholar
[K-L]Katok, A. & Lewis, J.. Local rigidity for certain groups of toral automorphisms. Israel J. Math. 75 (1991), 203–241.CrossRefGoogle Scholar
[K-S]Katok, A. & Spatzier, R.. Differentiable rigidity of hyperbolic abelian actions. Preprint. Math. Sci. Research Inst. Berkeley (1992).Google Scholar
[L-R]Langevin, R. & Rosenberg, H.. On stability of compact leaves and fibrations. Topology 16 (1977), 107–111.CrossRefGoogle Scholar
[Sc]Schmidt, W. M.. Diophantine Approximation. Springer Lecture Notes in Mathematics 785 Springer: Berlin, 1980.Google Scholar