Article contents
A characterization of relative Kazhdan property T for semidirect products with abelian groups
Published online by Cambridge University Press: 23 June 2010
Abstract
Let A be a locally compact abelian group, and H a locally compact group acting on A. Let G=H⋉A be the semidirect product, assumed σ-compact. We prove that the pair (G,A) has Kazhdan’s property T if and only if the only countably approximable H-invariant mean on the Borel subsets of the Pontryagin dual 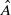 , supported at the neighbourhood of the trivial character, is the Dirac measure.
, supported at the neighbourhood of the trivial character, is the Dirac measure.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2010
References
- 6
- Cited by




