Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-16T10:14:28.323Z Has data issue: false hasContentIssue false
  • English
  • Français

A topological invariant for volume preserving diffeomorphisms

Published online by Cambridge University Press:  19 September 2008

Jean-Marc Gambaudo  and
Elisabeth Pécou
Jean-Marc Gambaudo
Affiliation:
Institut Non Linéaire de Nice, UMR CNRS 129, 1361, route des lucioles, 06560 Valbonne, France
Elisabeth Pécou
Affiliation:
Institut Non Linéaire de Nice, UMR CNRS 129, 1361, route des lucioles, 06560 Valbonne, France
Get access Rights & Permissions [Opens in a new window]

Abstract

For a smooth diffeomorphism f in ℝn+2, which possesses an invariant n-torus 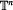, such that the restriction f 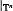is topologically conjugate to an irrational rotation, we define a number which represents the way the normal bundle to the torus 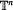asymptotically wraps around 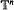. We prove that this number is a topological invariant among volume-preserving maps. This result can be seen as a generalization of a theorem by Naishul, for which we give a simple proof.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 15 , Issue 3 , June 1995 , pp. 535 - 541
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BG]Barge, J. and Ghys, E.. Cocycles d' Euler et Maslov. Math. Ann. 294 (1992), 235–265.CrossRefGoogle Scholar
[GST]Gambaudo, J. M., Sullivan, D. and Tresser, C.. Infinite cascades of braids and smooth dynamical systems. Topology. 33(1) (1994), 85–94.CrossRefGoogle Scholar
[Na]Naishul, V. A.. Topological invariant of analytic and area-preserving mappings and their application to analytic differential equations in C 2 and CP 2. Trans. Moscow Math. Soc. 2 (1982), 239–242.Google Scholar
[Ru]Ruelle, D.. Rotation numbers for diffeomorphisms and flows. Ann. Inst. Henri Poincaré 42 (Physique Théorique) (1985), 109–115.Google Scholar
[Sch]Schwartzmann, S.. Asymptotic cycles. Ann. Math. 66 (1957), 270–284.CrossRefGoogle Scholar