No CrossRef data available.
Article contents
Second-order ergodic theorem for self-similar tiling systems
Published online by Cambridge University Press: 04 July 2013
Abstract
We consider infinite measure-preserving non-primitive self-similar tiling systems in Euclidean space 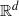 ${ \mathbb{R} }^{d} $. We establish the second-order ergodic theorem for such systems, with exponent equal to the Hausdorff dimension of a graph-directed self-similar set associated with the substitution rule.
${ \mathbb{R} }^{d} $. We establish the second-order ergodic theorem for such systems, with exponent equal to the Hausdorff dimension of a graph-directed self-similar set associated with the substitution rule.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2013




