Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Ergodic Theory and Dynamical Systems Ergodic Theory and Dynamical Systems

Article contents

On the existence of non-trivial homoclinic classes

Published online by Cambridge University Press:  01 October 2007

CHRISTIAN BONATTI ,
SHAOBO GAN  and
LAN WEN
CHRISTIAN BONATTI
Affiliation:
IMB, UMR 5584 du CNRS, BP 47870, 21078 Dijon Cedex, France (email: bonatti@u-bourgogne.fr)
SHAOBO GAN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China (email: gansb@math.pku.edu.cn, lwen@math.pku.edu.cn)
LAN WEN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China (email: gansb@math.pku.edu.cn, lwen@math.pku.edu.cn)
Corresponding
E-mail address:
bonatti@u-bourgogne.fr
gansb@math.pku.edu.cn
lwen@math.pku.edu.cn
Get access
Rights & Permissions[Opens in a new window]

Abstract

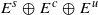We show that, for C1-generic diffeomorphisms, every chain recurrent class C that has a partially hyperbolic splitting with dimEc=1 either is an isolated hyperbolic periodic orbit, or is accumulated by non-trivial homoclinic classes. We also prove that, for C1-generic diffeomorphisms, any chain recurrent class that has a dominated splitting 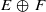with dim(E)=1 either is a homoclinic class, or the bundle E is uniformly contracting. As a corollary we prove in dimension three a conjecture of Palis, which announces that any C1-generic diffeomorphism is either Morse–Smale, or has a non-trivial homoclinic class.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 5 , October 2007 , pp. 1473 - 1508
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

[1]Birkhoff, G.. Dynamical Systems. American Mathematical Society, Providence, RI, 1966.Google Scholar
[2]Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
[3]Carballo, C., Morales, C. and Pacifico, M. J.. Maximal transitive sets with singularities for generic C1 vector fields. Bol. Soc. Brasil. Mat. (N.S.) 31(3) (2000), 287–303.CrossRefGoogle Scholar
[4]Conley, C.. Isolated Invariant Sets and the Morse Index (CBMS Regional Conference Series in Mathematics, 38). American Mathematical Society, Providence, RI, 1978.CrossRefGoogle Scholar
[5]Crovisier, S.. Periodic orbits and chain-transitive sets of C 1-diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.CrossRefGoogle Scholar
[6]Gan, S. and Wen, L.. Heteroclinic cycles and homoclinic closures for generic diffeomorphisms. J. Dynam. Differential Equations 15 (2003), 451–471.CrossRefGoogle Scholar
[7]Gourmelon, N.. Adapted metric for dominated splitting. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
[8]Hirsch, M., Pugh, C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, New York, 1977.CrossRefGoogle Scholar
[9]Liao, S. T.. Obstruction sets (II). Acta Sci. Natur. Univ. Pekinensis 2 (1981), 1–36.Google Scholar
[10]Mañé, R.. An ergodic closing lemma. Ann. of Math. (2) 116 (1982), 503–540.CrossRefGoogle Scholar
[11]Morales, C. and Pacifico, M. J.. Lyapunov stability of ω-limit sets. Discrete Contin. Dyn. Syst. 8(3) (2002), 671–674.Google Scholar
[12]Pliss, V. A.. On a conjecture of Smale. Differ. Uravn. 8 (1972), 268–282.Google Scholar
[13]Poincaré, H.. Les Méthodes Nouvelles de la Mécanique Céleste, 3 vols. Gauthier-Villars, Paris, 1899.Google Scholar
[14]Pugh, C.. The C 1-closing lemma. Amer. J. Math. 89 (1967), 956–1009.CrossRefGoogle Scholar
[15]Pujals, E. and Sambarino, M.. Homoclinic tangencies and hyperbolicity for surface diffeomorphisms. Ann. of Math. (2) 151(3) (2000), 961–1023.CrossRefGoogle Scholar
[16]Robinson, C.. Dynamical Systems. Stability, Symbolic Dynamics, and Chaos, 2nd edn(Studies in Advanced Mathematics). CRC Press, Boca Raton, FL, 1999.Google Scholar
[17]Wen, L.. Homoclinic tangencies and dominated splittings. Nonlinearity 15 (2002), 1445–1469.CrossRefGoogle Scholar
[18]Wen, L.. Generic diffeomorphisms away from homoclinic tangencies and heterodimensional cycles. Bull. Braz. Math. Soc. (N.S.) 35(3) (2004), 419–452.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 25 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 23rd January 2021. This data will be updated every 24 hours.

11 Cited by
Hostname: page-component-76cb886bbf-9l59n Total loading time: 0.583 Render date: 2021-01-23T23:58:19.042Z Query parameters: { "hasAccess": "0", "openAccess": "0", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

On the existence of non-trivial homoclinic classes
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

On the existence of non-trivial homoclinic classes
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

On the existence of non-trivial homoclinic classes
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *