Hostname: page-component-5c6d5d7d68-7tdvq Total loading time: 0 Render date: 2024-08-18T19:56:28.505Z Has data issue: false hasContentIssue false
  • English
  • Français

On the classification of some two-dimensional Markov shifts with group structure

Published online by Cambridge University Press:  19 September 2008

Mark A. Shereshevsky
Mark A. Shereshevsky
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, England
Get access Rights & Permissions [Opens in a new window]

Abstract

For a finite Abelian group G define the two-dimensional Markov shift 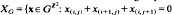for all 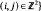. Let μG be the Haar measure on the subgroup 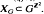. The group ℤ2 acts on the measure space (XG, MG) by shifts. We prove that if G1, and G2 are p-groups and E(G1,) ≠ E(G2), where E(G) is the least common multiple of the orders of the elements of G, then the shift actions on 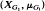and 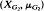are not measure-theoretically isomorphic. For any finite Abelian groups G1 and G2 the shift actions on 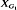and 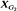are topologically conjugate if and only if G1 and G2 are isomorphic.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 12 , Issue 4 , December 1992 , pp. 823 - 833
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hardy, G. H. & Wright, E. M.. An Introduction to the Theory of Numbers. Oxford University Press, Oxford, 1975.Google Scholar
[2]Kitchens, B. & Schmidt, K.. Markov subgroups of . Israel J. Math. to appear.Google Scholar
[3]Kitchens, B. & Schmidt, K.. Mixing sets and relative entropies for higher-dimensional Markov shifts. University of Warwick, Preprint, 1991.Google Scholar
[4]Ledrappier, F.. Un champ markovien peut être d'enropie nulle et mélangeant. C. R. Acad. Sci. Paris, Ser. A, 287 (1987), 561–562.Google Scholar
[5]Schenkman, E.. Group Theory. Van Nostrand, New York, 1965.Google Scholar
[6]Schmidt, K.. Algebraic ideas in ergodic theory. CBMS Regional Conf. Ser. in Math., No. 76. American Mathematics Society, Providence RI, 1990.CrossRefGoogle Scholar
[7]Schmidt, K.. Automorphisms of compact abelian groups and affine varieties. Proc London Math. Soc. 61 (1990), 480–496.CrossRefGoogle Scholar
[8]Shereshevsky, M. A.. Ergodic properties of certain surjective cellular automata. Israel J. Math. to appear.Google Scholar
[9]Ward, T.. An algebraic obstruction to isomorphism of Markov shifts with group alphabet. Bull. London Math. Soc. to appear.Google Scholar