Article contents
Odd and even Maass cusp forms for Hecke triangle groups, and the billiard flow
Published online by Cambridge University Press: 04 August 2014
Abstract
By a transfer operator approach to Maass cusp forms and the Selberg zeta function for cofinite Hecke triangle groups, Möller and the present author found a factorization of the Selberg zeta function into a product of Fredholm determinants of transfer-operator-like families: 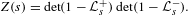 $$\begin{eqnarray}Z(s)=\det (1-{\mathcal{L}}_{s}^{+})\det (1-{\mathcal{L}}_{s}^{-}).\end{eqnarray}$$
$$\begin{eqnarray}Z(s)=\det (1-{\mathcal{L}}_{s}^{+})\det (1-{\mathcal{L}}_{s}^{-}).\end{eqnarray}$$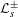 ${\mathcal{L}}_{s}^{\pm }$ arise as families of transfer operators for the triangle groups underlying the Hecke triangle groups, and that for
${\mathcal{L}}_{s}^{\pm }$ arise as families of transfer operators for the triangle groups underlying the Hecke triangle groups, and that for 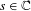 $s\in \mathbb{C}$,
$s\in \mathbb{C}$, 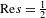 $\text{Re}s={\textstyle \frac{1}{2}}$, the operator
$\text{Re}s={\textstyle \frac{1}{2}}$, the operator 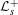 ${\mathcal{L}}_{s}^{+}$ (respectively
${\mathcal{L}}_{s}^{+}$ (respectively 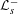 ${\mathcal{L}}_{s}^{-}$) has a 1-eigenfunction if and only if there exists an even (respectively odd) Maass cusp form with eigenvalue
${\mathcal{L}}_{s}^{-}$) has a 1-eigenfunction if and only if there exists an even (respectively odd) Maass cusp form with eigenvalue 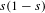 $s(1-s)$. For non-arithmetic Hecke triangle groups, this result provides a new formulation of the Phillips–Sarnak conjecture on non-existence of even Maass cusp forms.
$s(1-s)$. For non-arithmetic Hecke triangle groups, this result provides a new formulation of the Phillips–Sarnak conjecture on non-existence of even Maass cusp forms.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 5
- Cited by




