Article contents
Equilibrium measures for the Hénon map at the first bifurcation: uniqueness and geometric/statistical properties
Published online by Cambridge University Press: 02 October 2014
Abstract
For strongly dissipative Hénon maps at the first bifurcation parameter where the uniform hyperbolicity is destroyed by the formation of tangencies inside the limit set, we establish a thermodynamic formalism, i.e. we prove the existence and uniqueness of an invariant probability measure that minimizes the free energy associated with a non-continuous geometric potential 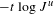 $-t\log J^{u}$, where
$-t\log J^{u}$, where 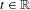 $t\in \mathbb{R}$ is in a certain large interval and
$t\in \mathbb{R}$ is in a certain large interval and 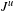 $J^{u}$ denotes the Jacobian in the unstable direction. We obtain geometric and statistical properties of these measures.
$J^{u}$ denotes the Jacobian in the unstable direction. We obtain geometric and statistical properties of these measures.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 10
- Cited by




