No CrossRef data available.
Article contents
Complete regularity of Ellis semigroups of  $\mathbb{Z} $-actions
$\mathbb{Z} $-actions
Published online by Cambridge University Press: 13 November 2020
Abstract
It is shown that the Ellis semigroup of a
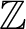 $\mathbb Z$
-action on a compact totally disconnected space is completely regular if and only if forward proximality coincides with forward asymptoticity and backward proximality coincides with backward asymptoticity. Furthermore, the Ellis semigroup of a
$\mathbb Z$
-action on a compact totally disconnected space is completely regular if and only if forward proximality coincides with forward asymptoticity and backward proximality coincides with backward asymptoticity. Furthermore, the Ellis semigroup of a
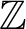 $\mathbb Z$
- or
$\mathbb Z$
- or
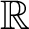 $\mathbb R$
-action for which forward proximality and backward proximality are transitive relations is shown to have at most two left minimal ideals. Finally, the notion of near simplicity of the Ellis semigroup is introduced and related to the above.
$\mathbb R$
-action for which forward proximality and backward proximality are transitive relations is shown to have at most two left minimal ideals. Finally, the notion of near simplicity of the Ellis semigroup is introduced and related to the above.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press





