INTRODUCTION
Bordetella pertussis causes the respiratory disease named whooping cough or pertussis that is most severe in infants. Before massive vaccination was introduced in the 1950s, pertussis was a major cause of infant mortality worldwide. As a consequence of the implementation of a pertussis immunization programme, a marked decline in disease incidence was observed [1, 2]. However, in the 1990s a resurgence of pertussis was detected in different countries and now pertussis has become the most prevalent vaccine-preventable disease in developed and in developing countries [Reference Baron3–Reference Hozbor5]. The disease is now recognized as a frequent infection not only for infants but also for adolescent and adults [Reference de Melker6]. Several explanations have been proposed for this resurgence of the disease, including improved surveillance, waning immunity and bacterial evolution [Reference Hozbor5, Reference Mooi7–Reference Yih10]. The relevance of these factors in the resurgence of pertussis might differ between countries. Beyond the possible causes, it is clear that the number of cases has steadily increased which undoubtedly marks the need to revise and implement strategies to improve the disease control. In fact, in 2002 different ministries of health, committees and organizations like the Global Pertussis Initiative (GPI, 2002), and Advisory Committee on Immunization Practices (ACIP) of the USA recommended expanding the existing vaccination strategies to include a pertussis booster dose for adolescents [Reference Forsyth11, 12]. The reported rationale for that strategy is to provide both direct protection for the adolescents that receive the booster and indirect benefit for non-immunized peers and the most vulnerable age groups, the infants. For this secondary but important goal, however, there is still no evidence showing a reduction in severe infant disease and mortality even following the implementation of an adolescent booster dose at age 11 years (Tdap) in different countries. Probably a few more years of data are needed to evaluate the real impact on infant disease before a universal recommendation could be considered.
Given this context, mathematical models of disease transmission contribute to a timely analysis of the impact of the new control strategies. In fact, an increasing number of papers on pertussis modelling have been reported [Reference Anderson and May13–Reference Rohani, Zhong and King20]. In this work we present an age-structured compartmental model to describe the propagation of pertussis in Argentina and to assess the impact of vaccination schedule changes on infant disease control. The model explores scenarios for future interventions in countries with social, demographic and epidemiological similarities to Argentina. Thus a brief overview of the Argentinean epidemiological situation is given before a description of the mathematical model.
Pertussis epidemiology in Argentina
Argentina is a South American country with a population of 40 091 359 inhabitants, and a high life expectancy (75·5 years) and literacy rate (97·7%), comparable to developed countries. From the beginning of pertussis vaccination in the 1970s and until 1985, the Argentinean schedule against pertussis included three primary doses of diphtheria-tetanus-whole cell pertussis vaccine (DTwP) at ages 2, 4 and 6 months and a booster dose of DTwP at 18 months. In 1985, a fifth DTwP dose at age 5–6 years (school entry) was introduced. Since 2009, in accord with international recommendations [Reference Forsyth21], an acellular pertussis booster dose (TdaP) was included for 11-year-olds and healthcare workers. All pertussis vaccine doses are distributed free of charge to the population. The three-dose pertussis coverage is high, typically 90%. In 2010 DTwP3 average coverage for Argentina was 92·8% [22]. However, this value is not uniform throughout the country because there are some regions with coverage lower than 80% [23]. The reported 18-month dose coverage is in general lower than the other doses. In 2010 the 11-year booster coverage was 57% [22]. In Argentina, as occurred in other countries, the introduction of mass immunization markedly decreased pertussis hospitalizations and deaths, reaching the lowest incidence levels in 2002 [23, Reference Riva Posse and Miceli24] (Fig. 1a). Figure 1a depicts the occurrence of pertussis outbreaks every 3–4 years, as was also reported for other countries [Reference Anderson and May25–Reference Broutin27]. These periodic outbreaks were also observed in different Argentinean districts in the vaccine era, and since the oscillations in incidence levels in the different districts are out of phase, the whole country oscillation becomes undetectable (Fig. 1b). Since 2002 an increase in pertussis incidence has been observed, which was sustained until the present (2012). During 2011, 8323 suspected pertussis cases were notified in the National Surveillance System (SIVILA). From these total cases, 6821 were registered in infants aged <1 year. The majority of these cases corresponded to the more populated provinces of Argentina such as Buenos Aires, Córdoba and Santa Fe. From those cases, 1663 (19·98%) were laboratory-confirmed pertussis cases. In 2010, 4981 cases were registered and 828 (16·62%) were laboratory confirmed. Again most of the cases were confirmed in patients aged <1 year (4217 from 4981). The large proportion of cases recorded in infants was not unexpected, since pertussis is most severe in this age group. The number of pertussis deaths during the analysed period of 2011 was around 70 (this value was extracted from national and local reports), recorded mostly in infants aged <1 year. As expected, young unvaccinated infants were more likely to have a severe disease, to suffer complications, to require hospitalization, or to die than older children and adults.

Fig. 1. (a) Pertussis incidence in Argentina during the 1969–2009 period. (b) Pertussis incidence in three Argentinean provinces. Pertussis incidence for the whole country is shown by dotted lines. (Source: SINAVE, Argentinean Ministry of Health.)
METHODS
Model
We developed a deterministic age-structured compartmental model to evaluate the effects of health policies on pertussis incidence in infants, mainly in the 0–1 year age group. The age discrimination allows us to simulate the application of vaccination doses at specific ages, as well as to explore the effect on pertussis transmission of different age profiles for the force of infection (FOI). The model described here is based on Hethcote's model designed in regard to pertussis in USA [Reference Hethcote15]. Here the population is stratified in nine epidemiological classes. Considering the severity of pertussis infection and consequently their infectivity, infected individuals were grouped into three classes: I1 for severe infection, I2 for mild infection, and I3 for weak infection. Individuals belonging to I1, I2, and I3 have decreasing infectivity. Populations that are susceptible to acquiring the infection are included in classes S, PAI1, PAI2, PAI3, but while individuals in S class (fully susceptible) have no immunity to the infection, PAI classes include individuals with partial acquired immunity via vaccination or natural infection. Classes R (recovered) and CAI (complete acquired immunity) include individuals fully protected against the disease.
The dynamics of pertussis propagation is simulated by transferring individuals in different classes at corresponding specific transfer rates (Fig. 2). In this model, individuals are in the susceptible class when born, and remain there unless: (a) they become infectious through contact with an infected individual and enter the full symptomatic infective class (I1), or (b) they acquire the lowest level of immunity through a vaccine dose and enter the PAI1 class. When receiving successive vaccination doses (indicated in Fig. 2 by dotted lines), individuals go through classes of increasing immunity and eventually reach the CAI class. Individuals in classes PAI1 and PAI2 may become infectious but they develop a less symptomatic illness entering class I2 (mild infection) or I3 (weak infection), respectively. We assume that infection fades in a time that is exponentially distributed around an average value 1/γ. After this time, individuals in infective classes I1, I2 or I3 recover and enter class R. Individuals in PAI3 class acquire an infection but it is so weak that they do not become infective and so directly enter R class. The main effect of infection on PAI3 individuals is to boost their own immunity, contributing to herd immunity.

Fig. 2. Schematic representation of the epidemiological model.
In this model we assume that immunity does not last lifelong. We consider that pertussis immunity is lost gradually. This effect was simulated by transferring individuals from the classes with complete immunity (R and CAI) to classes with decreasing degrees of immunity (PAI3 → PAI2 → PAI1). Individuals in classes R or CAI have complete immunity against infection for a typical time 1/σ or 1/τ, respectively, in order to account for the difference of duration of complete immunity if it has been acquired via infection or vaccination. We assume that further loss of immunity occurs at the same rate τ′, independently of the way it has been acquired. This is a simplification introduced in our model with respect to the one used by Hethcote [Reference Hethcote15]. We argue that with a careful choice of parameters σ, τ and τ′ we may account for the main effects that introduce the difference between natural and artificially acquired loss of immunity. Like Hethcote we consider the possibility that after a very long time individuals eventually become fully susceptible. In the model this fact was included by transferring individuals from PAI1 to S at a rate σ0. The nine epidemiological classes described above are divided into age groups. Thus, for fully susceptible individuals, for example, we define Si(t) as the fraction of individuals in class S, at time t, with age in the interval (a i, a i + 1). The FOI λi is the rate at which susceptible or partially immune individuals of age group i acquire infection. This is the only rate in our model that is not constant through time and depends on the fractions of infected individuals (which are dynamical variables of the model) through the expression:
where βij is the contact parameter matrix and Ij* is the effective fraction of individuals of age j in the population that is infective. Factors ρ1 and ρ2 are taken as smaller than 1 to consider that infected individuals in classes I2 and I3 are less infective than the ones in class I1 as they have a milder cough. The dynamics of the model is described by a set of coupled ordinary differential equations discussed in the Appendix where a detailed description of the model is included. By solving these equations, the population of the different classes discriminated by age group as a function of time can be obtained.
Model parameters
We define a set of ages: a i = 0, 2, 4, 6, 12, 18 months, yearly from 2 to 15 years; every 5 years from 15 to 55 years, and every 10 years from 55 to 75 years, which determines the n A = 30 age groups: (a i, a i + 1). For infants aged <18 months the ages were chosen taking into account the local vaccination schedule. In this work the size of population is considered constant in time (see Appendix). Concerning mortality rates, μi, in this work we assume that type I mortality (everybody dies at an age equal to life expectancy, see Appendix for details) is an acceptable approximation for Argentina (Supplementary Fig. S1, available online). Although it is well known that pertussis vaccination or infection does not provide lifelong immunity, the precise duration of protection is not known [Reference Wendelboe9, Reference Hethcote15, Reference Wearing and Rohani18]. Because of that, three immunity parameterizations were considered here: SDI, MDI and LDI for short, medium or long duration of immunity, respectively, based on data from Wendelboe et al. [Reference Wendelboe9]. It is assumed that the duration of natural immunity (t N) is the time elapsed since an individual has recovered from infection (enters class R) until reaching class PAI1 where the individual may acquire a mild infection. The duration of immunity acquired through vaccination (t V) is the time elapsed since an individual has been completely immunized (enters class CAI) until reaching class PAI1. Table 1 lists the values used for these parameters in the three immunity conditions considered. As in Hethcote's work, the efficacy of a pertussis vaccine dose (VE) was considered equal to 0·9 [Reference Hethcote15]. Taking into account that vaccine coverage in Argentina depends on the region [23], we considered both high vaccination coverage of 95% for the three-dose pertussis (C95) and low vaccination coverage of 80% for the three-dose pertussis (C80). In both cases, the 18-month dose coverage is lower than the other doses and was considered 85% and 70%, respectively, reaching the three-dose coverage for the 6-year boost (Table 2). The transmission of infection takes place through contact between infected and susceptible (or partially immunized) individuals. Quantitatively, this process is controlled by expression (1) for the FOI λi. Individuals with different grades of infection contribute differently to λi. This contribution was taken into account with the parameters ρ1 and ρ2. In particular the values used were those proposed by Hethcote: ρ1 = 0·5, ρ2 = 0·25 [Reference Hethcote15]. The recovery rate is set as γ = 1/(21 days) independently of the degree of infection. In order to determine βij contact parameters, two different procedures were followed, which led us to consider three different sets of contact parameters.
Table 1. Parameter values for the different pertussis immunity durations considered in this study
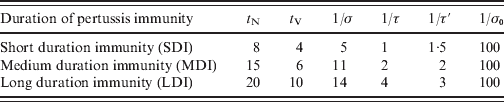
t N and t V are the duration of immunity acquired naturally (through infection) or artificially (through vaccination), respectively. The rates σ, τ and τ′ are chosen to obtain t N = 1/σ + 2/τ′, t V = 1/τ + 2/τ′. The rate at which immunized individuals become completely susceptible is controlled by the slow rate, σ0. All the values in the table are in years.
Table 2. Pertussis vaccination coverage for C95 and C80

The values of coverage included in the table are prior to the introduction of Tdap booster (at 11 years).
Procedure 1: Determination of contact parameters, βij, from the FOI and WAIFW (who acquires infection from whom) matrices
In the standard procedure described by Anderson & May [Reference Anderson and May25], βij is supposed to be symmetric among the age groups and some structure for matrix β is assumed in such a way that it has only few n B independent values. This structure is usually referred to as WAIFW matrix. If n B values of λi are known from epidemiological data, the given epidemiological model may be solved, the Ij* at the stationary state of the system may be obtained, and equation (1) is inverted in order to obtain the n B values that define βij. The details of this procedure and the minor modifications introduced by us in the present work are discussed in the Supplementary online material. A common practice in this parameterization procedure has been to take λi values from the pre-vaccine era and then use the βij parameters obtained in the vaccine era assuming that the contact structure of the population has not changed significantly [Reference Hethcote15, Reference Van Rie and Hethcote28]. There are, however, other models that parameterize βij from the knowledge of FOI in the vaccine era [Reference van Boven16, Reference Rozenbaum29]. A marked effort is currently made to obtain λi values from empirical data when the immunological situation is much more complicated than in the pre-vaccine era [Reference Kretzschmar, Teunis and Pebody30]. In Argentina, there are no sufficiently accurate age-stratified data to estimate λi values in the pre-vaccine or vaccine eras. Therefore, some standard λ age profiles of the pre-vaccine (case A) and vaccine (case B) eras are considered and discussed below.
FOI from the pre-vaccine era (case A)
The FOI in the pre-vaccine era could in principle be taken from any country because the pertussis epidemiological situation, before massive vaccination was implemented, was supposed to be similar in different countries. On the contrary, vaccination introduces several new variables such as coverage of vaccine formulations, time since application and age cohorts that have been vaccinated, which should be carefully considered when extrapolating parameters from one place to another. The values used here (shown in Fig. 3a) were based on those reported by Hethcote [Reference Hethcote15] with a slight modification in order to fit them in the age groups of our model. The relevant feature of this FOI profile is the peak for the 5–10 years age group. The average age at first infection, A 1st, estimated by our model (see Appendix) is between 4·4 and 5 years as expected for pertussis [Reference Anderson and May25]. It is important to note that as the determination of βij involves the solution of the epidemiological model, we obtain three sets of contact parameters (CP) one for each duration of immunity considered (SDI, MDI, LDI).

Fig. 3. Force of infection (FOI) for medium duration of immunity in the pre-vaccine era (–––) and vaccine era (- - -) with C95 coverage. Data in panels (a) and (b) have been used to parameterize the model in procedure 1, cases A and B, respectively. Panel (c) shows the FOI obtained with the model when procedure 2 is used to parameterize βij.
FOI based on studies in the vaccine era (case B)
In this case we follow a similar procedure as in case A but instead of taking the FOIs of the pre-vaccine era, we propose another procedure (see details in the Supplementary material). This procedure was developed in order that the FOI obtained with our model for the vaccine era shows some features recently observed in serological and demographic studies in several European countries [Reference Kretzschmar, Teunis and Pebody30]. These characteristics are: a peak of pertussis incidence for teenagers, the presence of a second broad peak at around age 45 years, and the fact that both peaks mostly share the same height (with the exception of Italy). The FOI both in the pre-vaccine and vaccine eras are shown in Figure 3b. The higher values of the FOI assigned to adults in comparison to case A, leads to higher values for the βij parameters that describe contacts among adults aged >35 years.
Procedure 2: Determination of βij from social contact patterns
βi,j parameters could also be determined from direct estimation of social contacts among different age groups. If a measurement of the rate c ij of the social contacts per day of an individual in age group i with individuals of age group j were available, βij could be approximated assuming that the probability of a contact being infective is the same for all age groups (see Supplementary material). An extensive study of social contacts in eight different European countries relevant for airborne or close-contact infectious diseases has been performed by Mossong and co-workers [Reference Mossong31]. These authors found that the eight sets of c ij obtained in the analysed countries, present similar qualitative features. We have used the statistical weighted average of the c ij reported in Mossong et al. [Reference Mossong31] to construct another possible contact pattern parameterization, even though the structure of social contacts in our country may present its intrinsic complexity. In Figure 3c we show the FOI predicted from this procedure for the MDI case in the pre-vaccine era.
A detailed description of the assumptions and methodology used to determine βij for procedures 1 and 2, and the resulting values are presented in the Supplementary material.
Epidemiological scenarios
In summary, for the parameterization of the model we consider different possible values for the three sets of parameters that define duration of immunity, contact patterns among people of different age groups and vaccine coverage. In Table 3 the notation used for these parameters is included. From these parameters 18 scenarios in the vaccine era were defined: SDI-CP1A-C95, MDI-CP1A-C95, LDI-CP1A-C95, SDI-CP1B-C80, … . It is important to note that each scenario is not the combination of independent parameters. While in the case of SDI, MDI, LDI, C95 and C80 each defines a set of parameter values, each CP refers to the procedure used to determine βij, but in order to obtain βij it is also necessary to give values to parameters that define the duration of immunity. For example, for CP1A we have three sets of βij, one for MDI, another for SDI and another for LDI.
Table 3. Pertussis epidemiological scenario parameters
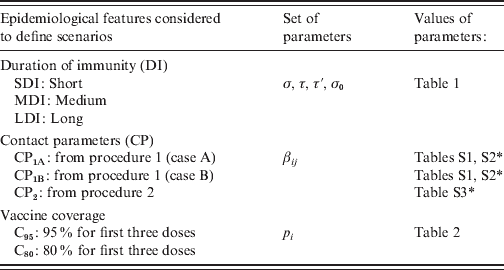
* See Supplementary tables in the online Supplementary material.
Each combination of DI-CP vaccine coverage defines a specific ‘scenario’.
RESULTS
Our study evaluates the impact of an adolescent booster dose (Tdap) on the most vulnerable 0–1 year age group using an age compartmental deterministic model. For all the calculations here presented we considered that coverage for Tdap dose is 85% even though the current coverage is 57%. This assumption was performed expecting that in the following years Tdap coverage will increase as was the case with the other vaccines introduced in the national immunization schedule.
Specific age incidences
The major focus of our attention was on pertussis incidence of fully (Inc1) and mild (Inc2) symptomatic pertussis cases, which are the most risky classes (infected and infective). These incidences may be computed for each age group as follows:
Inc1, in an age interval Δ, means the sum of Inc1i for all age groups contained in Δ. Specific age incidence (SAI) in interval Δ is defined as (Inc1 + Inc2)/Δ. Inc1 and Inc2 depend on time through the dynamical variables λi Si, PAIi1. However, all the results presented here and in the following section refer to the stationary values of incidences. We first focus on the CP1A-MDI scenario since contacts among individuals are based on standard FOIs that have been widely used by different authors [Reference Hethcote15, Reference Anderson and May25]. Regarding loss of immunity, MDI parameters correspond to the mean reported values and are similar to the ones used by Hethcote [Reference Hethcote15, Reference Hethcote32]. In this scenario SAIs for different age groups were calculated both in the pre-vaccine era and in the vaccine era with or without the extra dose at age 11 years. The results obtained are shown in Figure 4. The figure shows that in the pre-vaccine era, pertussis was an infection which mainly affected children. After the introduction of pertussis vaccine the incidence of disease in children declined markedly, particularly in the 0–5 years age group, where Inc1 + Inc2 decreased by a factor of 5. Although lower than in the pre-vaccine era, in the vaccine era a peak of pertussis incidence is detected in children in the 5–10 years age group. Moreover, in this era the SAI of adolescents aged 10–15 years is higher than that of the pre-vaccine era, probably as a consequence of the shorter duration of the immunity conferred by vaccination than that acquired by natural infection (Table 1). These changes in the calculated SAI caused by vaccination are in agreement with those previously reported in other studies that employed similar parameters to analyse pertussis in USA [Reference Hethcote15] and in Rio de Janeiro (Brazil) [Reference Luz17]. Figure 4 shows that the addition of the Tdap 11-year booster decreases the incidence of this age group but it has no significant effect on infants. We have even found that regardless the scenario considered the effect of adding an 11-year booster is still very small for children (Supplementary Fig. S2, online). Moreover, even when the coverage of the first five doses was low (C80) or the incidence in adolescents was particularly high, the inclusion of an extra Tdap booster would not improve the epidemiological situation of children (Supplementary Fig. S2).

Fig. 4. Effect of C95 vaccination schedule on the age-specific pertussis incidence for the CP1A-MDI scenario. Results considering an extra 11-year booster dose are also presented.
Incidences for infants aged <1 year
We then evaluated the effect of adolescent booster on pertussis incidence in infants aged <1 year for all scenarios analysed as shown in Table 4. We observed that beyond the differences in Inc1 and Inc2 in the scenarios considered, the effect of the addition of Tdap booster either on Inc1, Inc2 or Inc1 + Inc2 sum, is <5% in all cases. The effect of including the Tdap booster was also compared with the effect of improving the coverage of the first three doses. In Figure 5, the 0–1 year incidence (Inc1 + Inc2) values for the nine scenarios, for C95 and C80 coverage, are shown. It is clear that beyond the immunity duration or the contact scenario considered, improving vaccination coverage produces a significant decrease in 0–1 year incidence (between 22% and 32%) in comparison with the incorporation of the booster at age 11 years (below 5%). These data indicate that increasing the coverage of the first dose (at 2, 4 and 6 months) would result in a substantial improvement in the control of this disease.

Fig. 5. Effect of adolescent booster dosing on 0–1 year incidence (Inc1 + Inc2) in all scenarios for C95 and C80 coverage. Three durations of immunity were considered: short (upper panel), medium (middle panel) and long (lower panel).
Table 4. Effect of Tdap booster dosing on 0–1 year incidence
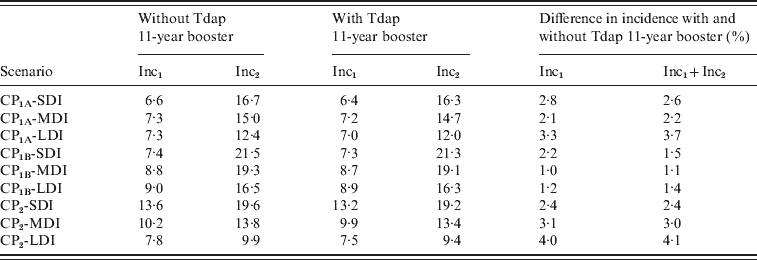
CP, Contact parameter; SDI, short duration immunity; MDI, medium duration immunity; LDI, long duration immunity.
Incidences are given in cases/year per 100 000 population.
Dynamical behaviour
The deterministic compartmental model presented here predicts that the system will reach a stationary equilibrium state that represents the endemic phase of the disease. Any disturbance of this equilibrium generates pronounced oscillations in the dynamical variables of the model that are smoothly damped over time. In particular, the introduction of the Tdap booster produces an oscillatory behaviour of incidence that is shown in Figure 6. The figure shows the dynamical evolution of Inc1(t) + Inc2(t) for 10 years for the 11–13 and 0–1 years age groups. Two years after introduction of the booster, when incidences attained their minimum, the drop of incidence observed in the figure for the 11–13 years group is about 47%, while for the 0–1 year group it is about 13%. Moreover, the incidence for the 11–13 years group oscillates around a new equilibrium value that is 43·5% lower than before the introduction of the booster. On the other side, in the 0–1 year group incidence oscillates around a value very similar to the one it had before introduction of the booster (only 2% lower). The oscillatory behaviour of pertussis incidence has been predicted by both stochastic and deterministic epidemic models [Reference Grenfell and Anderson14, Reference Wearing and Rohani18, Reference Rohani, Earn and Grenfell33]. The periods of outbreaks predicted by our model in the three MDI scenarios are shown in Table 5 and lie within the expected values for pertussis [Reference Anderson and May25–Reference Broutin27]. In particular, the observed period of 4 years for pertussis in Argentina (Fig. 1b) is well estimated by any of the scenarios considered. It should be noted that a precise prediction of the value of inter-epidemic period has remained very elusive as it depends on details in the model description, such as age dependence of the FOI [Reference Grenfell and Anderson14], a stochastic treatment of the fluctuations in the network of contacts where the disease spreads [Reference Simoes, Telo da Gama and Nunes34] and the consideration of deterministic recovery [Reference Simoes, Telo da Gama and Nunes34, Reference Gonçalves, Abramson and Gomes35]. Therefore, the results shown in Table 5 should not be interpreted as indicating that a certain scenario is better than another one because of a better prediction of the period of oscillations.

Fig. 6. Dynamical behaviour of incidence (Inc1 + Inc2) for the CP1A-MDI scenario with C95 vaccination coverage after introduction of the 11-year booster. Time is measured from the booster introduction.
Table 5. Inter-epidemic periods obtained for the MDI scenarios in the pre-vaccine and vaccine eras with C95 or C80 coverage
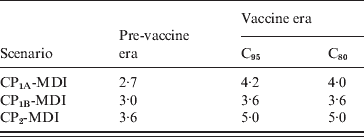
CP, Contact parameter; MDI, medium duration immunity.
Values given are in years.
Sensitivity of the previous results to different factors that may influence disease transmission
Variation of VE
Adequate estimates of VE per dose are difficult, particularly in our country, because Argentina uses imported vaccines from different companies which varies from year to year. Because of that in this work we use the value of 0·9 estimated by Hethcote from USA epidemiological data [Reference Hethcote15]. However, as VE enters our model as a multiplying factor of vaccine coverage p k, we may evaluate the effect of a lower VE when assessing the results for a lower coverage. Our results show that an adolescent booster has the same low effect in 0–1 year incidence when the coverage is reduced from 95% to 80%. Therefore, different VE values are not expected to modify the conclusions of our work.
Predicted effect of maternal immunity transmission (MIT) in newborn protection
Using our model we also analysed the effect of the transfer of immunity from mothers to infants in pertussis transmissibility. To this end, an extra class X0 was added to our model. This class includes individuals who acquired maternal antibodies and because of that, they would present mild symptomatology (I2) if they become infected. The modifications introduced to the model equations when MIT is considered are described in the Appendix. Performing calculations for the CP1A-MDI scenario, and assuming that maternal antibodies will last 2·5 years, we observed that MIT reduces the incidence Inc1 in the 0–1 year group by 10%. If we consider adolescent booster dosing, the effect of boosting in reducing 0–1 year incidence appears to be the same for this modified model that includes newborn protection as for the original model (typically 2%). Based on these results and using the modified model that includes the X0 class, a rough approximation of the effect that mother booster dosing would have on infant incidence was estimated. If we consider that 50% of mothers are immunized, the calculated reduction for Inc1 would lie around 33%. It should be noted that although this reduction in Inc1 is associated directly with an equal increase in Inc2, it is a desirable effect since the severe form of the disease in children is reduced. In fact, the decrease of the full infection in the most vulnerable population with highest risk of hospitalization and death, is one of the goals pursued by the health system. The results presented in this section agree with the recommendations recently made by the ACIP of the USA CDC related to the use of Tdap vaccine in pregnant women [12].
Analysis of the effect of immune memory on pertussis transmission
There is evidence that immune memory cells exposed again to an antigen through infection or a complete vaccination scheme exhibit a more efficient response than naive cells. Therefore it is reasonable to suppose that a pertussis booster vaccination in individuals who have had a previous pertussis infection or at least three vaccine doses would confer the highest degree of immunity. We considered this effect in our model sending those individuals that exhibit a more efficient response directly to class CAI when a booster is applied independently of their presence in class PAI1, PAI2 or PAI3. These modifications were introduced in our model (see Appendix for details) and the computations of incidence for CP1A-MDI scenarios repeated. The results (Table 6) point out that, even though the 11-year dose is predicted to be more effective by this modified model, it still shows a low impact on young infant incidence (below 5%). In any case, the introduction of the adolescent booster in the vaccination schedule displays a minor effect in reducing incidence in the 0–1 year group. This memory effect was also considered by other authors in SIR-based models including three types of partial immunity classes: removed, vaccinated and waning immunity classes [Reference Hethcote32].
Table 6. Comparative analysis of the effect of Tdap booster dosing on the 0–1 year incidence simulated using unmodified and modified models
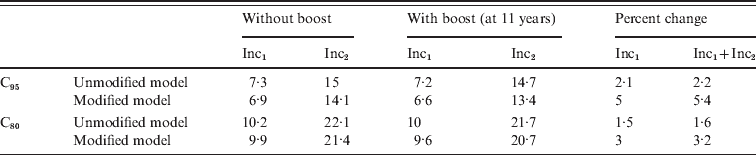
Calculations were performed for the CP1A-MDI scenario with C95 or C80 coverage.
In the modified model immunity memory effects are taken into account by subdividing classes PAI1 and PAI2 (see Appendix for more details).
Another way in which immune memory may affect pertussis transmission has recently been analysed by Lavine et al. [Reference Lavine, King and Bjornstad19]. These authors considered in their transmission model that individuals could receive frequent natural boosters when exposed to a small number of bacteria. This possibility was also considered in our model taking a rate κλ instead of λ for individuals that go from PAI3 to R class (see Fig. 2). When considering the CP2-MDI scenario taking κ = 2, our results show that in the vaccine era (C95) the system presents pronounced epidemic outbreaks similar to those obtained by Lavine et al. for high coverage [Reference Lavine, King and Bjornstad19] with no stationary state. Even when the dynamical description of the system predicted by our model when considering this boosting effect is very different, the values of mean incidence for infants are very similar. In particular, the effect of adding the 11-year booster in infants implies a 3% reduction of 0–1 year incidence, as we have previously shown for our model (see Table 4). A detailed study of the consequences of introducing this effect in our model of pertussis transmission is beyond the scope of the present work and will be addressed elsewhere.
DISCUSSION
With the recommended application of the Tdap booster in adolescents, not only a reduction in adolescent pertussis incidence is expected but also an indirect benefit for infants could be achieved. This last objective seems to be feasible since the immunization of adolescents would remove at least in part the source of infection for infants. However, since currently there is no evidence to support this rationale, it is difficult to produce a universal recommendation to extend vaccination programmes to adolescents. Given this situation and to promptly assess the impact of the adolescent booster in infants, we designed a deterministic age-structured compartmental model based on two assumptions regarding pertussis immunity and transmission that are largely agreed upon: immunity has an important effect on the severity of disease, and immunity wanes over time. In this sense, the population in our model is stratified in nine classes (Fig. 2). With this model different possible epidemiological scenarios (n = 18) were explored since there are uncertainties in some parameters such as the rate of infectious contacts between people of different ages and also the exact duration of protective immunity.
In the 18 scenarios considered we could reproduce not only the drop in the incidence of children caused by the massive use of pertussis vaccine but also the fact that the SAI of the 10–15 years group was higher in the vaccine era than in the pre-vaccine era. These features reproduced here were evidenced by epidemiological studies in several countries [Reference Brooks and Clover36] and different models [Reference Hethcote15, Reference Luz17]. It is important to note, however, that the magnitudes of the vaccine effects calculated here do not correlate with the data reported, probably due to underreporting of the disease. The general consensus is that the reported cases are probably much lower than the true incidence of pertussis. Because of this underreporting, the total pertussis incidence in the vaccine era predicted by the model, are much higher than those reported by national surveillance systems. The magnitude of the observed incidence reduction in Argentina due to vaccination (Fig. 1) is predicted by the model only for the incidence of fully symptomatic cases, Inc1. This is the case, for example, for the calculated value of Inc1 in the 0–5 years age group which is reduced by a factor of 75 from the pre-vaccine to the vaccine endemic equilibrium in the CP1A-MDI-C95 scenario. This agreement between the reported data and the calculated values of children (Inc1) was also found in simulations of pertussis in USA [Reference Hethcote15] and supports the idea that the health system mainly detects child fully-symptomatic cases. The above-mentioned underreporting would be more pronounced in adolescents or adults where normal prolonged cough may be the only clinical feature. This underreporting makes it difficult to use notified data to decide which of the 18 scenarios is the best fit to reality. Following this rationale, different scenarios were considered to perform our analysis.
To evaluate the effect of the incorporation of the 11-year Tdap in the National Vaccination Schedule, we performed calculations for all considered scenarios. The results obtained showed that the 11-year Tdap booster decreases the incidence of the disease in this age group. This result is in agreement with the reported [Reference Quinn and McIntyre37, Reference Skoff38] and predicted [Reference Rozenbaum29] data. When the effect of the introduction of an adolescent booster in infants was analysed, our results showed that the Tdap booster also reduces incidence in infants but to a very low extent. The calculated decrease does not exceed 5% for any of the scenarios considered. Since none of the variations included in the epidemiological scenarios leads to a reduction higher than 5%, the prediction of the model proves to be robust. This result is in agreement with those reported by other authors using different models and parameterizations to obtain similar results [Reference Lavine, King and Bjornstad19, Reference Rozenbaum29]. Moreover, in some stochastic models in which it is considered that pertussis immunity is not lost, the reinforcement at 11 years does not impact in reducing the incidence in infants [Reference Rohani, Zhong and King20]. All these studies suggest that widespread adolescent vaccinations may not bring about the reduction in pertussis cases some had hoped. This could be explained at least in part by the relatively low weight that adolescents have as a source of infection in infants [Reference Jardine39–Reference Wendelboe41]. In fact, a recent work shows that adolescents exhibit different seasonal pertussis peaks compared to infants, suggesting that children and adults (possibly parents), not adolescents, are the main sources of infant infection [Reference Lavine42]. The outcome of immunization of the relatively low fraction of adolescents that is a source of infant infection could be even lower because of Tdap efficacy, coverage and duration of immunity which do not ensure that the whole adolescent population is protected by the booster. This rationale supports the results predicted by our model.
Importantly, using our model we were able to demonstrate that, in countries such as Argentina where some regions have relatively low vaccine coverage, improving coverage of the first dose has a more beneficial impact in reducing incidence in infants than the vaccination of adolescents. In fact, a key outcome of our study is that increasing coverage of the first dose (at 2, 4 and 6 months) from 80% to 95%, would result in a substantial reduction on infant incidence in all scenarios considered (between 22% and 32%). However, in countries with a high coverage, a reduction of 5% in incidence could be assessed as positive. In this sense, Rosenbaum, using an age-structured compartmental deterministic model found that among several proposed vaccination strategies for The Netherlands (where coverage of first dose is 96%) the optimum one is the addition of 12-year booster dose which produces a 5·5% reduction in infant infection [Reference Rozenbaum29]. Beyond the high vaccination coverage that could be achieved in a country, there are other strategies that may be better than vaccination in adolescents. In this sense modifications performed in our model evidence that vaccination of mothers during pregnancy would be a more effective strategy to protect infants than vaccination of adolescents. These results are consistent with recent widespread recommendations on vaccination of mothers after 20 weeks of gestation [12].
In summary, in this work we evaluate the Tdap booster impact on infant incidence considering some features relevant to pertussis transmission. We worked in the framework of deterministic compartmental age-structured models and have studied several epidemiological scenarios covering a wide range and combination of parameters. The impact of the Tdap booster on infants was also assessed by modifying our model in order to include the effect of transmission of mother immunity and the memory immune response of individuals. The results obtained showed that our predictions concerning the effect of Tdap booster in infants are robust. It is important to mention, however, that there are some other aspects of pertussis transmission that we have not explored as they introduce further complexities or they exceed the framework of our model and will be considered in depth in future work. This is the case of stochastic effects, heterogeneity of contacts because of social membership or regionality, changes in circulating bacteria, and several correlations that could be introduced properly in an agent-based model.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0950268812001380.
ACKNOWLEDGEMENTS
A. Melgarejo, A. Lodeiro, A. Graieb and I. Miceli are acknowledged for fruitful discussions. We thank Celina Castuma and M. Quiroga for the English revision. This work was supported by Agencia Nacional de Promoción Científica y Tecnológica-ANCPyT, Comisión de Investigaciones Científicas de Buenos Aires-CICBA and Consejo Nacional de Investigaciones Científicas y Tecnológicas-CONICET (Argentina) grants to D.F.H. and G.F. G.F. and P.B. are members of the Scientific Career of CONICET. D.F.H. is a member of the Scientific Career of CICBA.
DECLARATION OF INTEREST
None.
APPENDIX
Mathematical description of the model
In our model individuals are assigned to one of the nine epidemiological classes S, PAI1, PAI2, PAI3, CAI, I1, I2, I3, and R, based on their immunity to pertussis and infection status. We also define an age set: a 0, a 1, a 2, …, and divide the population into age groups, where the age of the individuals in age group ‘i’ is in the interval: (a i, a i + 1). The epidemiological state of the population is specified by the fraction of individuals (with respect to the total population) in each one of the epidemiological classes: Si, PAIi1, PAIi2, PAIi3, CAIi, I1i, I2i, I3i, Ri, for each one of the n A age groups, i = 0, …, n A – 1. The dynamical evolution of these variables monitors the propagation of the disease and is described by the following set of ordinary first-order coupled differential equations:
 $$\left.\eqalign{\tab {{{\rm dS}_{i} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm S}_{i} \plus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \mu _{i} {\rm S}_{i} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm S}_{i \minus \setnum{1}} \minus c_{i} {\rm S}_{i} \plus \delta _{i \setnum{0}} B \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm S}_{i \minus \setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{3}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \sigma {\rm R} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}} \cr \tab {{{\rm dC}_{{\rm AI}i} } \over {{\rm d}t}} \equals \minus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm C}_{{\rm AI}i} {_{ \minus \setnum{1}}} \minus c_{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \cr \tab {{{\rm dI}_{\setnum{1}i}} \over {{\rm d}t}} \equals \lambda _{i} {\rm S}_{i} \minus \gamma {\rm I}_{\setnum{1}i} \minus \mu _{i} {\rm I}_{\setnum{1}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{1}{ i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{1}i} \cr \tab {{{\rm dI}_{\setnum{2}i} } \over {{\rm d}t}} \equals \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \gamma {\rm I}_{\setnum{2}i} \minus \mu _{i} {\rm I}_{\setnum{2}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{2}{i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{2}i} \cr \tab {{{\rm dI}_{\setnum{3}i} } \over {{\rm d}t}} \equals \lambda_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \gamma {\rm I}_{\setnum{3}i} \minus \mu _{i} {\rm I}_{\setnum{3}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{3}{i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{3}i} \cr \tab {{{\rm dR}_{i} } \over {{\rm d}t}} \equals \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \gamma \lpar {\rm I}_{\setnum{1}i} \plus {\rm I}_{\setnum{2}i} \plus {\rm I}_{\setnum{3}i} \rpar \minus \sigma {\rm R} \minus \mu _{i} {\rm R} \plus c_{i \minus \setnum{1}} {\rm R}_{i \minus \setnum{1}} \minus c_{i} {\rm R}_{i} \cr}\right\} $$
$$\left.\eqalign{\tab {{{\rm dS}_{i} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm S}_{i} \plus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \mu _{i} {\rm S}_{i} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm S}_{i \minus \setnum{1}} \minus c_{i} {\rm S}_{i} \plus \delta _{i \setnum{0}} B \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm S}_{i \minus \setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{3}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \tau ^\prime{\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \sigma {\rm R} \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}} \cr \tab {{{\rm dC}_{{\rm AI}i} } \over {{\rm d}t}} \equals \minus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm C}_{{\rm AI}i} {_{ \minus \setnum{1}}} \minus c_{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \cr \tab {{{\rm dI}_{\setnum{1}i}} \over {{\rm d}t}} \equals \lambda _{i} {\rm S}_{i} \minus \gamma {\rm I}_{\setnum{1}i} \minus \mu _{i} {\rm I}_{\setnum{1}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{1}{ i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{1}i} \cr \tab {{{\rm dI}_{\setnum{2}i} } \over {{\rm d}t}} \equals \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}} \minus \gamma {\rm I}_{\setnum{2}i} \minus \mu _{i} {\rm I}_{\setnum{2}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{2}{i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{2}i} \cr \tab {{{\rm dI}_{\setnum{3}i} } \over {{\rm d}t}} \equals \lambda_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}} \minus \gamma {\rm I}_{\setnum{3}i} \minus \mu _{i} {\rm I}_{\setnum{3}i} \plus c_{i \minus \setnum{1}} {\rm I}_{\setnum{3}{i \minus \setnum{1}}} \minus c_{i} {\rm I}_{\setnum{3}i} \cr \tab {{{\rm dR}_{i} } \over {{\rm d}t}} \equals \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \gamma \lpar {\rm I}_{\setnum{1}i} \plus {\rm I}_{\setnum{2}i} \plus {\rm I}_{\setnum{3}i} \rpar \minus \sigma {\rm R} \minus \mu _{i} {\rm R} \plus c_{i \minus \setnum{1}} {\rm R}_{i \minus \setnum{1}} \minus c_{i} {\rm R}_{i} \cr}\right\} $$In writing these equations we assume that the total population is constant in time. Even though the annual mean growth rate in Argentina was 9·6% in the 2000–2005 period, this is a reasonable approximation considering we are not interested in describing the dynamics of the model during long time intervals. For a similar model Hethcote has considered a variation of the total population with time for propagation of pertussis in USA throughout 100 years. His results show, that even for this long time lapse, patterns of incidences and age distributions are not considerably affected by considering a constant population size [Reference Hethcote15]. The rates σ, σ0, τ, τ′ and γ are constant in time and have been defined in the Methods (Models) section, μi is the mortality rate for age group i, and c i is the rate at which individuals are transferred from an age group to the next because of ageing. We take c i = 1/(a i + 1 – a i) for i = 0, …, n A – 2, in that way, for class I1 for example, in an interval Δt a fraction Δt/(a i – a i − 1) of individuals in age group i – 1 are transferred to group i because of ageing, while a fraction Δt/(a i + 1 – a i) leaves group i to enter i + 1. Note that there is no younger group than i = 0 or older than n A – 1, so we take ![]() $c_{ \minus \setnum{1}} \equals c_{n_{\rm A} \minus \setnum{1}} \equals 0$ in order to cancel the corresponding terms in the set of differential equations. Vaccination is taken into account by transferring individuals from the S or PAI classes to the following increased immunity class when a vaccine dose is applied. This is introduced in the model through the function vacci, the fraction of individuals at age a i that are successfully immunized. For example, if a dose is applied at age a i, the rate c i, at which individuals are transferred from Si − 1 to Si because of ageing [first equation in (A1)], has to be multiplied by a factor (1 – vacci) because the immunized individuals have been added to PAIi1 in the last term of the second equation. So, vacci is different from 0 only when a i coincides with the age of one of the application doses, d k,
$c_{ \minus \setnum{1}} \equals c_{n_{\rm A} \minus \setnum{1}} \equals 0$ in order to cancel the corresponding terms in the set of differential equations. Vaccination is taken into account by transferring individuals from the S or PAI classes to the following increased immunity class when a vaccine dose is applied. This is introduced in the model through the function vacci, the fraction of individuals at age a i that are successfully immunized. For example, if a dose is applied at age a i, the rate c i, at which individuals are transferred from Si − 1 to Si because of ageing [first equation in (A1)], has to be multiplied by a factor (1 – vacci) because the immunized individuals have been added to PAIi1 in the last term of the second equation. So, vacci is different from 0 only when a i coincides with the age of one of the application doses, d k,
where f k is the fraction of people at age d k successfully immunized, p k is the coverage of k dose, n d is the number of doses applied, and VE the vaccine efficacy. In order that this scheme works, ages a i have to be chosen in such a way that each d k coincides with some a i.
The last term in the first equation of the system (A1) represents the birth rate. The symbol δ is the Kroenecker delta, so, δi0 indicates that the term is present only for i = 0. In principle, we assume that every individual is born susceptible, so B is the per capita birth rate and is included in the equation for S0. In order to keep the total population constant, B should equal the per capita mortality rate, so we take
where N i is the fraction of the population in age group i.
The FOI is the rate at which a susceptible (or partially immune) individual in age group ‘i’ acquires infection, and it is calculated as follows:
where ![]() c(i, j) is the number of infective contacts per unit of time between an individual of age group i with individuals of age group j, and (Ij*/N j) represents the effective probability that an individual in age group ‘j’ is infective. For ‘infective contact’ we mean a contact such that if an individual in group j is fully infected (I1) and an individual in group i is partially or completely susceptible, then an individual in group i will acquire infection. The contact parameter matrix, βij=
c(i, j) is the number of infective contacts per unit of time between an individual of age group i with individuals of age group j, and (Ij*/N j) represents the effective probability that an individual in age group ‘j’ is infective. For ‘infective contact’ we mean a contact such that if an individual in group j is fully infected (I1) and an individual in group i is partially or completely susceptible, then an individual in group i will acquire infection. The contact parameter matrix, βij=![]() c(i,j)/N j, gives a measure of the contact rate between individuals of different age groups that is independent of age group sizes.
c(i,j)/N j, gives a measure of the contact rate between individuals of different age groups that is independent of age group sizes.
Once a choice of all the parameters is made, an initial epidemiological state for the population is chosen, and the system of equations (A1) is solved numerically by Euler integration taking a small enough time interval, Δt, until the stationary state is reached.
Modifications introduced to the model in order to account for the effect of MIT in newborn protection
We add to our model an extra class X0. This class includes individuals who acquired maternal antibodies and because of that if they became infected, they would present mild symptomatology (I2). Since it is known that the duration of maternal antibodies does not exceed 2 months, the fraction of individuals in X0 that are not vaccinated with the corresponding 2-month dose would go directly to the susceptible class. In contrast, the X0 fraction that gets vaccinated would move to class PAI1. At this point it is important to note that the new class X0 included in the model is formed only by the 0–2 months age group. Assuming that mother's antibodies will last τA since they entered class R and that the typical time that the individuals spend in class R is 1/σ, the fraction of mothers that are able to transmit antibodies to their babies is f A = σ⋅τARM. Where RM is the fraction of mothers in class R (fraction of individuals aged between 20 and 35 years that are in class R). With these assumptions, f A represents the fraction of newborns that go to class X0, and 1 – f A represents the fraction that goes to class S. The time evolution of the fraction of individuals in class X0 is given by the equation:
All other equations of the model remain the same as in (A1), with the exception of those given below:
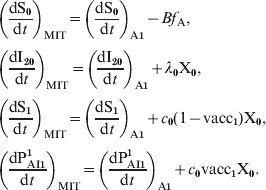 $$\openup 3pt{ \eqalign{\tab \left( {{{{\rm dS}_{\setnum{0}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dS}_{\setnum{0}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \minus Bf_{\rm A}\comma \cr \tab \left( {{{{\rm dI}_{\setnum{2}{\setnum{0}}}} \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dI}_{\setnum{2}{\setnum{0}}}} \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus \lambda _{\setnum{0}} {\rm X}_{\setnum{0}}\comma \cr \tab \left( {{{{\rm dS}_{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dS}_{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus c_{\setnum{0}} \lpar 1 \minus {\rm vacc}_{\setnum{1}} \rpar {\rm X}_{\setnum{0}}\comma \cr \tab \left( {{{{\rm dP}_{{\rm AI}\setnum{1}} ^{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dP}_{{\rm AI}\setnum{1}} ^{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus c_{\setnum{0}} {\rm vacc}_{\setnum{1}} {\rm X}_{\setnum{0}}. \cr}} \hfill$$
$$\openup 3pt{ \eqalign{\tab \left( {{{{\rm dS}_{\setnum{0}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dS}_{\setnum{0}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \minus Bf_{\rm A}\comma \cr \tab \left( {{{{\rm dI}_{\setnum{2}{\setnum{0}}}} \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dI}_{\setnum{2}{\setnum{0}}}} \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus \lambda _{\setnum{0}} {\rm X}_{\setnum{0}}\comma \cr \tab \left( {{{{\rm dS}_{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dS}_{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus c_{\setnum{0}} \lpar 1 \minus {\rm vacc}_{\setnum{1}} \rpar {\rm X}_{\setnum{0}}\comma \cr \tab \left( {{{{\rm dP}_{{\rm AI}\setnum{1}} ^{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm MIT}} \equals \left( {{{{\rm dP}_{{\rm AI}\setnum{1}} ^{\setnum{1}} } \over {{\rm d}t}}} \right)_{{\rm A\setnum{1}}} \plus c_{\setnum{0}} {\rm vacc}_{\setnum{1}} {\rm X}_{\setnum{0}}. \cr}} \hfill$$where the subindex MIT denotes the magnitude considering maternal immunity transmission and the subindex A1 denotes the expression given in the formula (A1). Taking τM = 2·5 years we obtain for the CP1A-MDI scenario: f A = 0·12.
Modifications introduced to the model in order to account for the effect of immune memory on pertussis transmission
In order to consider the more efficient response exhibited by individuals that have been previously immunized (via infection or three vaccine doses), the classes PAI1 and PAI2 were subdivided into two subclasses, one containing individuals that come from S class (with naive cells) and other containing those that come from PAI3 class (with immune memory cells). The fraction of individuals in classes PAI1 and PAI2 and age group i is written:
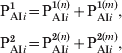 $$\openup3pt{\eqalign{ {\rm P}_{{\rm AI}i} ^{\setnum{1}} \tab \equals {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \comma \cr {\rm P}_{{\rm AI}i} ^{\setnum{2}} \tab \equals {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \comma}} \hfill $$
$$\openup3pt{\eqalign{ {\rm P}_{{\rm AI}i} ^{\setnum{1}} \tab \equals {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \comma \cr {\rm P}_{{\rm AI}i} ^{\setnum{2}} \tab \equals {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \comma}} \hfill $$where we have explicitly separated the contributions from individuals with naive cells (n) and immune memory cells (m). Both these subclasses then evolve in time in an independent way with the following difference: when individuals in an n subclass receive a vaccine dose, they increase their immunity gradually following the dynamics of Figure 2 (PAI1 → PAI2 → PAI3), while individuals in an m subclass go directly to class CAI when vaccinated. The dynamics are described by the following equations:
 $$\eqalign{\tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \minus \sigma _{\setnum{0}}{\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}{i \minus \setnum{1}}} ^{\setnum{1}\lpar n\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm S}_{i \minus \setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \minus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \plus \tau ^\prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar m\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar n\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar n\rpar } \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \plus \tau ^\prime {\rm P}_{{\rm AI}i} ^{\setnum{3} } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar m\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } }\hfill < $$> <$$> \eqalign{\tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{3}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \sigma R \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}{i \minus \setnum{1}}}^{\setnum{2} \lpar n\rpar } \cr \tab {{d{\rm C}_{{\rm AI}i} } \over {{\rm d}t}} \equals \minus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm C}_{{\rm AI}i \minus \setnum{1}} \minus c_{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar m\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar m\rpar }} \hfill$$
$$\eqalign{\tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \minus \sigma _{\setnum{0}}{\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}{i \minus \setnum{1}}} ^{\setnum{1}\lpar n\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar n\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm S}_{i \minus \setnum{1}} \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \minus \sigma _{\setnum{0}} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \plus \tau ^\prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar m\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{1}\lpar m\rpar } \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar n\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar n\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar n\rpar } \cr \tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \plus \tau ^\prime {\rm P}_{{\rm AI}i} ^{\setnum{3} } \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar m\rpar } \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{2}\lpar m\rpar } }\hfill < $$> <$$> \eqalign{\tab {{{\rm dP}_{{\rm AI}i} ^{\setnum{3}} } \over {{\rm d}t}} \equals \minus \lambda _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \minus \tau^ \prime {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus \sigma R \plus c_{i \minus \setnum{1}} \lpar 1 \minus {\rm vacc}_{i} \rpar {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \minus c_{i} {\rm P}_{{\rm AI}i} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}{i \minus \setnum{1}}}^{\setnum{2} \lpar n\rpar } \cr \tab {{d{\rm C}_{{\rm AI}i} } \over {{\rm d}t}} \equals \minus \tau {\rm C}_{{\rm AI}i} \minus \mu _{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm C}_{{\rm AI}i \minus \setnum{1}} \minus c_{i} {\rm C}_{{\rm AI}i} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{3}} \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{2}\lpar m\rpar } \plus c_{i \minus \setnum{1}} {\rm vacc}_{i} {\rm P}_{{\rm AI}i \minus \setnum{1}} ^{\setnum{1}\lpar m\rpar }} \hfill$$where the equations for the time derivatives of Si, I1i, I2i, I 3i and Ri are the same as in (A1).
Age at first infection
We estimate the average age at first infection, A 1st, through the expression
where A i = (a i + 1+a i)/2 and the sums are limited to include individuals with ages lower than a given A max in order to avoid returning to the S class of adults. In our model, immunized adults lose their immunity and are allowed to become susceptible at a very low rate σ0, but they should not be considered in the evaluation of A 1st. We only compute A 1st in the pre-vaccine era and observe that it takes a reasonable value when A max is between ages 10 and 20 years, when most ‘first infections’ have already occurred.
Type I mortality
In this approximation it is assumed that everybody dies exactly at an age equal to the life expectancy: L [Reference Anderson and May25]. In the present work all the mortality rates μi are 0 with the exception of that corresponding to the oldest group, i = n A – 1, which takes the value: ![]() $1\sol \lpar a_{n_{\rm A} } \minus a_{n_{\rm A} \minus \setnum{1}} \rpar $. As the total population is constant, all the N i are also constant: N i = (a i + 1 – a i)/L, and the birth rate is B = 1/L.
$1\sol \lpar a_{n_{\rm A} } \minus a_{n_{\rm A} \minus \setnum{1}} \rpar $. As the total population is constant, all the N i are also constant: N i = (a i + 1 – a i)/L, and the birth rate is B = 1/L. ![]() $L \equals a_{n_{\rm A} } $ (the highest age considered) = 75 years in this work.
$L \equals a_{n_{\rm A} } $ (the highest age considered) = 75 years in this work.
















