Article contents
A Subspace-Projected Approximate Matrix Method for Systems of Linear Equations
Published online by Cambridge University Press: 28 May 2015
Abstract
Given two n × n matrices A and A0 and a sequence of subspaces 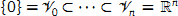 with dim
with dim 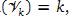 the k-th subspace-projected approximated matrix Ak is defined as Ak = A + Πk(A0 − A)Πk, where Πk is the orthogonal projection on
the k-th subspace-projected approximated matrix Ak is defined as Ak = A + Πk(A0 − A)Πk, where Πk is the orthogonal projection on 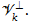 . Consequently, Akν = Aν and ν*Ak = ν*A for all
. Consequently, Akν = Aν and ν*Ak = ν*A for all 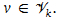 Thus
Thus 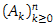 is a sequence of matrices that gradually changes from A0 into An = A. In principle, the definition of
is a sequence of matrices that gradually changes from A0 into An = A. In principle, the definition of 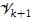 may depend on properties of Ak, which can be exploited to try to force Ak+1 to be closer to A in some specific sense. By choosing A0 as a simple approximation of A, this turns the subspace-approximated matrices into interesting preconditioners for linear algebra problems involving A. In the context of eigenvalue problems, they appeared in this role in Shepard et al. (2001), resulting in their Subspace Projected Approximate Matrix method. In this article, we investigate their use in solving linear systems of equations Ax = b. In particular, we seek conditions under which the solutions xk of the approximate systems Akxk = b are computable at low computational cost, so the efficiency of the corresponding method is competitive with existing methods such as the Conjugate Gradient and the Minimal Residual methods. We also consider how well the sequence (xk)k≥0 approximates x, by performing some illustrative numerical tests.
may depend on properties of Ak, which can be exploited to try to force Ak+1 to be closer to A in some specific sense. By choosing A0 as a simple approximation of A, this turns the subspace-approximated matrices into interesting preconditioners for linear algebra problems involving A. In the context of eigenvalue problems, they appeared in this role in Shepard et al. (2001), resulting in their Subspace Projected Approximate Matrix method. In this article, we investigate their use in solving linear systems of equations Ax = b. In particular, we seek conditions under which the solutions xk of the approximate systems Akxk = b are computable at low computational cost, so the efficiency of the corresponding method is competitive with existing methods such as the Conjugate Gradient and the Minimal Residual methods. We also consider how well the sequence (xk)k≥0 approximates x, by performing some illustrative numerical tests.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2013
References
- 1
- Cited by




