Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Compositio Mathematica Compositio Mathematica

Article contents

Spaces of rational curves on complete intersections

Part of: Special varieties Cycles and subschemes

Published online by Cambridge University Press:  26 March 2013

Roya Beheshti  and
N. Mohan Kumar
Roya Beheshti
Affiliation:
Department of Mathematics, Washington University in St. Louis, St. Louis, MO 63130, USA (email: beheshti@wustl.edu)
N. Mohan Kumar
Affiliation:
Department of Mathematics, Washington University in St. Louis, St. Louis, MO 63130, USA (email: kumar@wustl.edu)
Save pdf (0.48 mb)
Rights & Permissions[Opens in a new window]

Abstract

We prove that the space of smooth rational curves of degree $e$ on a general complete intersection of multidegree 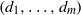$(d_1, \ldots , d_m)$ in 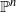$\mathbb {P}^n$ is irreducible of the expected dimension if 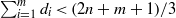$\sum _{i=1}^m d_i \lt (2n+m+1)/3$ and $n$ is sufficiently large. This generalizes a result of Harris, Roth and Starr [Rational curves on hypersurfaces of low degree, J. Reine Angew. Math. 571 (2004), 73–106], and is achieved by proving that the space of conics passing through any point of a general complete intersection has constant dimension if 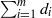$\sum _{i=1}^m d_i$ is small compared to $n$ .

Keywords

hypersurface rational curves Hilbert scheme

MSC classification

Secondary: 14M10: Complete intersections 14M22: Rationally connected varieties 14C05: Parametrization (Chow and Hilbert schemes)
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 6 , June 2013 , pp. 1041 - 1060
Copyright
Copyright © 2013 The Author(s) 

References

[BM96]Behrend, K. and Manin, Yu., Stacks of stable maps and Gromov–Witten invariants, Duke Math. J. 85 (1996), 1–60.CrossRefGoogle Scholar
[CS09]Coskun, I. and Starr, J., Rational curves on smooth cubic hypersurfaces, Int. Math. Res. Not. 2009 (2009), 4626–4641.Google Scholar
[Deb01]Debarre, O., Higher dimensional algebraic geometry (Springer, New York, 2001).CrossRefGoogle Scholar
[dJS04]de Jong, A. J. and Starr, J., Cubic fourfolds and spaces of rational curves, Illinois J. Math. 48 (2004), 415–450.Google Scholar
[dJS06]de Jong, A. J. and Starr, J., Low degree complete intersections are rationally simply connected, Preprint (2006).Google Scholar
[Del04]Deland, M., Geometry of rational curves on algebraic varieties, PhD thesis, Columbia University (2004).Google Scholar
[Ein86]Ein, L., Varieties with small dual varieties I, Invent. Math. 86 (1986), 63–74.CrossRefGoogle Scholar
[FP97]Fulton, W. and Pandharipande, R., Notes on stable maps and quantum cohomology, in Algebraic geometry: Santa Cruz 1995, Proceedings of Symposia in Pure Mathematics, vol. 62 eds Kollár, J., Lazarsfeld, R. and Morrison, D. (American Mathematical Society, Providence, RI, 1997).Google Scholar
[HRS04]Harris, J., Roth, M. and Starr, J., Rational curves on hypersurfaces of low degree, J. Reine Angew. Math. 571 (2004), 73–106.Google Scholar
[Har77]Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).CrossRefGoogle Scholar
[Kle74]Kleiman, S. L., The transversality of a general translate, Compositio Math. 28 (1974), 287–297.Google Scholar
[Kol96]Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, vol. 32 (Springer, Berlin, 1996).CrossRefGoogle Scholar
[Mat86]Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, Cambridge, 1986).Google Scholar
[Mum70]Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5 (Oxford University Press, Oxford, 1970).Google Scholar
[Sta04]Starr, J., The Kodaira dimension of spaces of rational curves on low degree hypersurfaces, Preprint (2004).Google Scholar
[Vak00]Vakil, R., The enumerative geometry of rational and elliptic curves in projective space, J. Reine Angew. Math. 529 (2000), 101–153.Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 108 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 20th January 2021. This data will be updated every 24 hours.

Access
8 Cited by
Hostname: page-component-76cb886bbf-m9qpn Total loading time: 0.542 Render date: 2021-01-20T14:28:06.092Z Query parameters: { "hasAccess": "1", "openAccess": "0", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Spaces of rational curves on complete intersections
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Spaces of rational curves on complete intersections
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Spaces of rational curves on complete intersections
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *