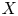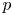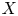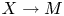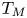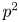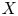1. Introduction
1.1 Positivity of tangent bundles
Mori's celebrated proof of the Hartshorne conjecture asserts that a smooth projective variety ![]() $X$ over an arbitrary algebraically closed field is isomorphic to a projective space
$X$ over an arbitrary algebraically closed field is isomorphic to a projective space ![]() $\mathbb {P}^n$ if and only if the tangent bundle satisfies the positivity condition called ample [Reference MoriMor79]. This characterization of projective spaces is the algebro-geometric counterpart of the Frankel conjecture in complex geometry, which was proved by [Reference Siu and YauSY80].
$\mathbb {P}^n$ if and only if the tangent bundle satisfies the positivity condition called ample [Reference MoriMor79]. This characterization of projective spaces is the algebro-geometric counterpart of the Frankel conjecture in complex geometry, which was proved by [Reference Siu and YauSY80].
As an attempt to generalize this kind of characterization, Campana and Peternell started the study of complex projective varieties satisfying a numerical semipositivity condition, called nef (see § 2 for the definition). Philosophically, if the tangent bundle is semipositive, then the variety is expected to decompose into the ‘positive’ part and the ‘flat’ part. Indeed, after the series of papers by Campana and Peternell [Reference Campana and PeternellCP91, Reference Campana and PeternellCP93], this type of decomposition has been accomplished by Demailly, Peternell, and Schneider.
Theorem 1.1 ([Reference Demailly, Peternell and SchneiderDPS94, Main theorem],  $/\mathbb {C}$)
$/\mathbb {C}$)
If the tangent bundle of a complex projective manifold ![]() $X$ is nef, then, up to an étale cover, the variety
$X$ is nef, then, up to an étale cover, the variety ![]() $X$ admits a fibration over an abelian variety whose fibers
$X$ admits a fibration over an abelian variety whose fibers ![]() $F$ are Fano varieties (varieties with ample anti-canonical divisor
$F$ are Fano varieties (varieties with ample anti-canonical divisor ![]() $-K_F$).
$-K_F$).
This decomposition theorem reduces the study of varieties with nef tangent bundles to that of Fano varieties. Campana and Peternell conjectured that Fano varieties with nef tangent bundles are rational homogeneous varieties ![]() $G/P$, where
$G/P$, where ![]() $G$ is a semisimple algebraic group and
$G$ is a semisimple algebraic group and ![]() $P$ is a parabolic group [Reference Campana and PeternellCP91, 11.2].
$P$ is a parabolic group [Reference Campana and PeternellCP91, 11.2].
Main tools to study Fano varieties are the theory of rational curves and Mori's theory of extremal rays. From the view point of Mori's theory, rational homogeneous spaces ![]() $G/P$ share an important feature that their contractions are always smooth. In the same paper [Reference Demailly, Peternell and SchneiderDPS94], Demailly, Peternell, and Schneider also proved the following fundamental structure theorem.
$G/P$ share an important feature that their contractions are always smooth. In the same paper [Reference Demailly, Peternell and SchneiderDPS94], Demailly, Peternell, and Schneider also proved the following fundamental structure theorem.
Theorem 1.2 ([Reference Demailly, Peternell and SchneiderDPS94, Theorem 5.2] and [Reference Solá Conde and WiśniewskiSW04, Theorem 4.4],  $/\mathbb {C}$)
$/\mathbb {C}$)
Let ![]() $X$ be a smooth complex projective variety and assume that
$X$ be a smooth complex projective variety and assume that ![]() $T_X$ is nef. Then any
$T_X$ is nef. Then any ![]() $K_X$-negative extremal contraction
$K_X$-negative extremal contraction ![]() $f \colon X \to Y$ is smooth.
$f \colon X \to Y$ is smooth.
This theorem provides an evidence for the validity of the Campana–Peternell conjecture. In fact, it plays an important role in the course of partial proofs of the Campana–Peternell conjecture [Reference Campana and PeternellCP91, Reference Campana and PeternellCP93, Reference MokMok02, Reference HwangHwa06, Reference WatanabeWat14, Reference WatanabeWat15, Reference KanemitsuKan16, Reference KanemitsuKan17, Reference Muñoz, Occhetta, Solá Conde and WatanabeMOSW15, Reference Solá Conde and WiśniewskiSW04]. We also refer the reader to [Reference Muñoz, Occhetta, Solá Conde, Watanabe and WiśniewskiMOSW+15] for an account of the Campana–Peternell conjecture.
The purpose of this paper is to establish the analogous results for varieties with nef tangent bundle in positive characteristic. Note that the proofs in [Reference Demailly, Peternell and SchneiderDPS94] depend on analytic arguments, which we cannot directly apply in positive characteristic case (for details, see § 1.7). Thus, we will take a different strategy based on the Mori theory. The rough idea is to use an analogue of Theorem 1.2 to obtain the decomposition theorem: by taking successive extremal contractions, each of which is a smooth morphism, we find a smooth morphism ![]() $\varphi : X \to M$ such that
$\varphi : X \to M$ such that ![]() $T_{M}$ is numerically flat and any fiber of
$T_{M}$ is numerically flat and any fiber of ![]() $\varphi$ is rationally chain connected (RCC). Then, by proving that the fibers of
$\varphi$ is rationally chain connected (RCC). Then, by proving that the fibers of ![]() $\varphi$ are Fano varieties, we obtain our decomposition theorem. Thus, the key step is to give a characterization of Fano varieties with nef tangent bundles or, more precisely, to study varieties with nef tangent bundle which contain many rational curves.
$\varphi$ are Fano varieties, we obtain our decomposition theorem. Thus, the key step is to give a characterization of Fano varieties with nef tangent bundles or, more precisely, to study varieties with nef tangent bundle which contain many rational curves.
In the rest of this section, unless otherwise stated, ![]() $k$ denotes an algebraically closed field of positive characteristic
$k$ denotes an algebraically closed field of positive characteristic ![]() $p >0$, and
$p >0$, and ![]() $X$ is a smooth projective variety defined over
$X$ is a smooth projective variety defined over ![]() $k$.
$k$.
1.2 Rational curves on varieties with nef tangent bundle
Recall that a Fano variety ![]() $X$ is RCC (see [Reference MoriMor79, Theorem 5], [Reference CampanaCam92], and [Reference Kollár, Miyaoka and MoriKMM92a, Theorem 3.3]). In characteristic zero, rational chain connectedness of
$X$ is RCC (see [Reference MoriMor79, Theorem 5], [Reference CampanaCam92], and [Reference Kollár, Miyaoka and MoriKMM92a, Theorem 3.3]). In characteristic zero, rational chain connectedness of ![]() $X$, in turn, implies that there exists a highly unobstructed rational curve
$X$, in turn, implies that there exists a highly unobstructed rational curve ![]() $\mathbb {P}^1 \to X$ called very free rational curve, whose existence is equivalent to a stronger rational connectedness notion, that
$\mathbb {P}^1 \to X$ called very free rational curve, whose existence is equivalent to a stronger rational connectedness notion, that ![]() $X$ is separably rationally connected (SRC) [Reference Kollár, Miyaoka and MoriKMM92b, Theorem 2.1] (see also Definition 3.1).
$X$ is separably rationally connected (SRC) [Reference Kollár, Miyaoka and MoriKMM92b, Theorem 2.1] (see also Definition 3.1).
The first theorem of this article asserts that, if ![]() $T_X$ is nef, then the same also holds in positive characteristic.
$T_X$ is nef, then the same also holds in positive characteristic.
Theorem 1.3 (RCC  $\implies$ SRC)
$\implies$ SRC)
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume that
$k$ and assume that ![]() $T_X$ is nef. If
$T_X$ is nef. If ![]() $X$ is RCC, then
$X$ is RCC, then ![]() $X$ is SRC.
$X$ is SRC.
Thus, if ![]() $X$ is RCC, then
$X$ is RCC, then ![]() $X$ contains a very free rational curve. By [Reference DebarreDeb03, Corollaire 3.6], [Reference ShenShe10, Corollary 5.3], [Reference Biswas and Dos SantosBD13], and [Reference GounelasGou14], we have the next corollary.
$X$ contains a very free rational curve. By [Reference DebarreDeb03, Corollaire 3.6], [Reference ShenShe10, Corollary 5.3], [Reference Biswas and Dos SantosBD13], and [Reference GounelasGou14], we have the next corollary.
Corollary 1.4 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume that
$k$ and assume that ![]() $T_X$ is nef. If
$T_X$ is nef. If ![]() $X$ is RCC, then the following hold:
$X$ is RCC, then the following hold:
(1)
 $X$ is algebraically simply connected, i.e. any connected finite étale cover of
$X$ is algebraically simply connected, i.e. any connected finite étale cover of  $X$ is trivial;
$X$ is trivial;(2)
 $H^1(X, \mathcal {O}_X) = 0$;
$H^1(X, \mathcal {O}_X) = 0$;(3) every numerically flat vector bundle on
 $X$ is trivial.
$X$ is trivial.
1.3 Contractions of extremal rays
Recall that, over an arbitrary algebraically closed field ![]() $k$, Mori's cone theorem holds [Reference MoriMor82]. Namely, the Kleiman–Mori cone
$k$, Mori's cone theorem holds [Reference MoriMor82]. Namely, the Kleiman–Mori cone ![]() $\overline {\operatorname {NE}} (X)$ is locally polyhedral in
$\overline {\operatorname {NE}} (X)$ is locally polyhedral in ![]() $K_X$-negative side and, thus, it decomposes as follows:
$K_X$-negative side and, thus, it decomposes as follows:
where ![]() $R_i = \mathbb {R}_{\geq 0}[C_i]$ are
$R_i = \mathbb {R}_{\geq 0}[C_i]$ are ![]() $K_X$-negative extremal rays, each of which is spanned by a class of a rational curve
$K_X$-negative extremal rays, each of which is spanned by a class of a rational curve ![]() $C_i$. Note that, in characteristic zero, each extremal ray is realized in a geometrical way, i.e. there exists the contraction of each extremal ray
$C_i$. Note that, in characteristic zero, each extremal ray is realized in a geometrical way, i.e. there exists the contraction of each extremal ray ![]() $R$ (see, e.g., [Reference Kollár and MoriKM98]), while the existence of extremal contractions is widely open in positive characteristic. The following theorem asserts that, if
$R$ (see, e.g., [Reference Kollár and MoriKM98]), while the existence of extremal contractions is widely open in positive characteristic. The following theorem asserts that, if ![]() $T_X$ is nef, then the contraction of an extremal ray exists and, in fact, it is smooth.
$T_X$ is nef, then the contraction of an extremal ray exists and, in fact, it is smooth.
Theorem 1.5 (Existence and smoothness of contractions)
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume that
$k$ and assume that ![]() $T_X$ is nef.
$T_X$ is nef.
Let ![]() $R \subset \overline {\operatorname {NE}} (X)$ be a
$R \subset \overline {\operatorname {NE}} (X)$ be a ![]() $K_X$-negative extremal ray. Then the contraction
$K_X$-negative extremal ray. Then the contraction ![]() $f \colon X \to Y$ of
$f \colon X \to Y$ of ![]() $R$ exists and the following hold:
$R$ exists and the following hold:
(1)
 $f$ is smooth;
$f$ is smooth;(2) any fiber
 $F$ of
$F$ of  $f$ is an SRC Fano variety with nef tangent bundle;
$f$ is an SRC Fano variety with nef tangent bundle;(3)
 $T_Y$ is again nef.
$T_Y$ is again nef.
See also Corollary 6.1 for contractions of extremal faces.
1.4 Decomposition theorem
To prove the decomposition theorem, we first construct a smooth morphism ![]() $X \to M$ whose fibers are RCC and image
$X \to M$ whose fibers are RCC and image ![]() $M$ has numerically flat tangent bundle
$M$ has numerically flat tangent bundle ![]() $T_M$. The following theorem ensures that the fibers are Fano varieties.
$T_M$. The following theorem ensures that the fibers are Fano varieties.
Theorem 1.6 (RCC  $\implies$ Fano)
$\implies$ Fano)
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume that
$k$ and assume that ![]() $T_X$ is nef. If
$T_X$ is nef. If ![]() $X$ is RCC, then
$X$ is RCC, then ![]() $X$ is a smooth Fano variety. Moreover, the Kleiman–Mori cone
$X$ is a smooth Fano variety. Moreover, the Kleiman–Mori cone ![]() $\operatorname {NE}(X)$ of
$\operatorname {NE}(X)$ of ![]() $X$ is simplicial.
$X$ is simplicial.
Remark 1.7 In fact, the above assertion also holds in relative settings (see Theorem 5.3).
By combining the above theorems we can obtain the decomposition theorem of varieties with nef tangent bundle.
Theorem 1.8 (Decomposition theorem)
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume that
$k$ and assume that ![]() $T_X$ is nef. Then
$T_X$ is nef. Then ![]() $X$ admits a smooth contraction
$X$ admits a smooth contraction ![]() $\varphi \colon X \to M$ such that:
$\varphi \colon X \to M$ such that:
(1) any fiber of
 $\varphi$ is a smooth SRC Fano variety with nef tangent bundle;
$\varphi$ is a smooth SRC Fano variety with nef tangent bundle;(2)
 $T_M$ is numerically flat.
$T_M$ is numerically flat.
Remark 1.9 Since there are no rational curves on varieties with numerically flat tangent bundles, the morphism ![]() $\varphi$ is the maximally rationally chain connected (MRCC) fibration in the sense of [Reference KollárKol96, Chapter IV, § 5].
$\varphi$ is the maximally rationally chain connected (MRCC) fibration in the sense of [Reference KollárKol96, Chapter IV, § 5].
1.5 Questions
The above decomposition theorem reduces the study of varieties with nef tangent bundle to two cases (the Fano case and the ![]() $K_X$-trivial case). The following suggests the possible structures of varieties in these two cases.
$K_X$-trivial case). The following suggests the possible structures of varieties in these two cases.
Question 1.10 ([Reference Campana and PeternellCP91, Conjecture 11.1], [Reference WatanabeWat17, Question 1])
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$ and assume
$k$ and assume ![]() $T_X$ is nef.
$T_X$ is nef.
(1) If
 $X$ is a Fano variety, then is
$X$ is a Fano variety, then is  $X$ a homogeneous space
$X$ a homogeneous space  $G/P$, where
$G/P$, where  $G$ is a semisimple algebraic group and
$G$ is a semisimple algebraic group and  $P$ is a parabolic subgroup?
$P$ is a parabolic subgroup?(2) If
 $K_X \equiv 0$ or, equivalently,
$K_X \equiv 0$ or, equivalently,  $T_X$ is numerically flat, then is
$T_X$ is numerically flat, then is  $X$ an étale quotient of an abelian variety?
$X$ an étale quotient of an abelian variety?
Note that, in characteristic zero, the second assertion is true by virtue of the Beauville–Bogomolov–Yau decomposition, which is studied intensively in characteristic positive [Reference Patakfalvi and ZdanowiczPZ20], but is still open. See also [Reference Mehta and SrinivasMS87, Reference LiLi10, Reference LangerLan15, Reference WatanabeWat17, Reference JoshiJos21] for partial answers and related topics on the above question.
1.6 Application
In the last part of this paper, we will apply our results to the study of ![]() $F$-liftable varieties. A smooth projective variety
$F$-liftable varieties. A smooth projective variety ![]() $X$ (over an algebraically closed field of positive characteristic) is said to be
$X$ (over an algebraically closed field of positive characteristic) is said to be ![]() $F$-liftable, if it lifts modulo
$F$-liftable, if it lifts modulo ![]() $p^2$ with the Frobenius morphism (see Definition 7.1 for the precise definition). The known examples of
$p^2$ with the Frobenius morphism (see Definition 7.1 for the precise definition). The known examples of ![]() $F$-liftable varieties are toric varieties and ordinary abelian varieties. Conversely, any
$F$-liftable varieties are toric varieties and ordinary abelian varieties. Conversely, any ![]() $F$-liftable variety is expected to decompose into these two types of varieties.
$F$-liftable variety is expected to decompose into these two types of varieties.
Conjecture 1.11 [Reference Achinger, Witaszek and ZdanowiczAWZ21, Conjecture 1]
Let ![]() $Z$ be an
$Z$ be an ![]() $F$-liftable variety. Then there exists a finite Galois cover
$F$-liftable variety. Then there exists a finite Galois cover ![]() $f \colon Y \to Z$ such that the Albanese morphism
$f \colon Y \to Z$ such that the Albanese morphism ![]() $\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a toric fibration.
$\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a toric fibration.
This conjecture is confirmed only in the case of homogeneous varieties [Reference Buch, Thomsen, Lauritzen and MehtaBTLM97, Reference Achinger, Witaszek and ZdanowiczAWZ21]. In fact, in [Reference Achinger, Witaszek and ZdanowiczAWZ21, Proposition 6.3.2], the conjecture is verified when ![]() $X$ is a Fano manifold with nef tangent bundle whose Picard number is one. Here we apply our study to show that the conjecture holds under a more general situation that
$X$ is a Fano manifold with nef tangent bundle whose Picard number is one. Here we apply our study to show that the conjecture holds under a more general situation that ![]() $T_X$ is nef.
$T_X$ is nef.
Theorem 1.12 ( $F$-liftable varieties with nef tangent bundle)
$F$-liftable varieties with nef tangent bundle)
If ![]() $X$ is
$X$ is ![]() $F$-liftable and
$F$-liftable and ![]() $T_X$ is nef, then there exists a finite étale Galois cover
$T_X$ is nef, then there exists a finite étale Galois cover ![]() $f \colon Y \to X$ such that the Albanese morphism
$f \colon Y \to X$ such that the Albanese morphism ![]() $\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a smooth morphism onto an ordinary abelian variety whose fibers are products of projective spaces.
$\alpha _{Y} \colon Y \to \operatorname {Alb} (Y)$ is a smooth morphism onto an ordinary abelian variety whose fibers are products of projective spaces.
1.7 Differences between our proofs and proofs in complex analytic case
Here we summarize major differences between our proofs and the proofs in [Reference Demailly, Peternell and SchneiderDPS94].
At first, we review the proof of Theorem 1.1 (which is [Reference Demailly, Peternell and SchneiderDPS94, Main theorem]). Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $\mathbb {C}$ and assume that
$\mathbb {C}$ and assume that ![]() $T_X$ is nef. In the course of their study, Demailly, Peternell, and Schneider first proved the following assertions [Reference Demailly, Peternell and SchneiderDPS94, Proposition 3.9 and Proposition 3.10] (see also [Reference Campana and PeternellCP91, Proposition 2.4]).
$T_X$ is nef. In the course of their study, Demailly, Peternell, and Schneider first proved the following assertions [Reference Demailly, Peternell and SchneiderDPS94, Proposition 3.9 and Proposition 3.10] (see also [Reference Campana and PeternellCP91, Proposition 2.4]).
(1) The Albanese map
 $X \to \operatorname {Alb}(X)$ is a smooth morphism.
$X \to \operatorname {Alb}(X)$ is a smooth morphism.(2) If
 $(-K_X)^{\dim X}>0$, then
$(-K_X)^{\dim X}>0$, then  $X$ is a Fano variety.
$X$ is a Fano variety.(3) If
 $(-K_X)^{\dim X}=0$, then there exists a finite étale cover of
$(-K_X)^{\dim X}=0$, then there exists a finite étale cover of  $X$ whose irregularity is positive.
$X$ whose irregularity is positive.
Then, by repeatedly applying these assertions, they find an appropriate étale cover of ![]() $X$ whose Albanese map decomposes
$X$ whose Albanese map decomposes ![]() $X$ into Fano part and abelian part. Note that the proof of the above assertions heavily relies on three analytic ingredients (the complex analytic description of the Albanese maps, the Kodaira vanishing theorem, and the Hodge theory), which fail in positive characteristic. Note also that the conclusion of Theorem 1.1 immediately implies that varieties with numerically flat tangent bundle are étale quotients of abelian varieties, while this characterization is still unknown in positive characteristic (see Question 1.10).
$X$ into Fano part and abelian part. Note that the proof of the above assertions heavily relies on three analytic ingredients (the complex analytic description of the Albanese maps, the Kodaira vanishing theorem, and the Hodge theory), which fail in positive characteristic. Note also that the conclusion of Theorem 1.1 immediately implies that varieties with numerically flat tangent bundle are étale quotients of abelian varieties, while this characterization is still unknown in positive characteristic (see Question 1.10).
In positive characteristic, we will take the Mori theoretic view point, and obtain the decomposition theorem (Theorem 1.8) by proving the following assertions:
– characterization of Fano varieties with nef tangent bundles (Theorems 1.3 and 1.6; Fano
 $\iff$ SRC
$\iff$ SRC  $\iff$ RCC);
$\iff$ RCC);– existence and smoothness of contractions (Theorem 1.5).
Our proof is sketched as follows: By taking successive ![]() $K$-negative contractions of extremal rays (each of which is a smooth morphism, thanks to Theorem 1.5), we find a smooth morphism
$K$-negative contractions of extremal rays (each of which is a smooth morphism, thanks to Theorem 1.5), we find a smooth morphism ![]() $\varphi : X \to M$ such that
$\varphi : X \to M$ such that ![]() $T_{M}$ is numerically flat and any fiber of
$T_{M}$ is numerically flat and any fiber of ![]() $\varphi$ is RCC. Then, by applying the characterization of Fano varieties, we obtain our decomposition theorem. The most essential part of our approach is to prove Theorem 1.3 (RCC
$\varphi$ is RCC. Then, by applying the characterization of Fano varieties, we obtain our decomposition theorem. The most essential part of our approach is to prove Theorem 1.3 (RCC ![]() $\implies$ SRC), which is used in both proofs of Theorem 1.5 (existence and smoothness of contractions) and Theorem 1.6 (RCC
$\implies$ SRC), which is used in both proofs of Theorem 1.5 (existence and smoothness of contractions) and Theorem 1.6 (RCC ![]() $\implies$ Fano).
$\implies$ Fano).
1.8 Outline of the paper
This article is organized as follows. In § 2, we provide a preliminaries on nef vector bundles.
In § 3, we study the SRC varieties with nef tangent bundle and prove Theorem 1.3. The main ingredient of the proof is Shen's theorem that provides a relation between being SRC and foliations in positive characteristic [Reference ShenShe10]. By using this relation, we construct a purely inseparable finite morphism ![]() $X \to Y$ (if
$X \to Y$ (if ![]() $X$ is RCC) such that
$X$ is RCC) such that ![]() $Y$ also has nef tangent bundle and is SRC. From this morphism
$Y$ also has nef tangent bundle and is SRC. From this morphism ![]() $X \to Y$, we can construct an action of the group scheme
$X \to Y$, we can construct an action of the group scheme ![]() $G = \mu _p$ or
$G = \mu _p$ or ![]() $\alpha _p$ on
$\alpha _p$ on ![]() $Y$ without fixed points. Then, by following Kollár's proof of simple connectedness of SRC varieties [Reference DebarreDeb03, Corollaire 3.6], we will have a contradiction and, hence,
$Y$ without fixed points. Then, by following Kollár's proof of simple connectedness of SRC varieties [Reference DebarreDeb03, Corollaire 3.6], we will have a contradiction and, hence, ![]() $X$ itself is SRC.
$X$ itself is SRC.
In § 4, we study extremal contractions on varieties with nef tangent bundle and prove Theorem 1.5. Theorem 1.5 essentially follows from the arguments of [Reference KanemitsuKan22, Theorem 2.2] and [Reference Solá Conde and WiśniewskiSW04, Lemma 4.12], while we use Theorem 1.3 to adapt these arguments in the positive characteristic case.
In § 5, we will prove Theorem 1.6. In fact, we will study the relative Kleiman–Mori cone ![]() $\operatorname {NE} (X/Y)$ of a contraction
$\operatorname {NE} (X/Y)$ of a contraction ![]() $f \colon X \to Y$ with RCC fibers. The main theorem of this section is Theorem 5.3, which proves that the cone
$f \colon X \to Y$ with RCC fibers. The main theorem of this section is Theorem 5.3, which proves that the cone ![]() $\operatorname {NE} (X/Y)$ is simplicial cone spanned by
$\operatorname {NE} (X/Y)$ is simplicial cone spanned by ![]() $K_X$-negative extremal rays. The proof essentially goes the same way as that of [Reference WatanabeWat21, Proof of Theorem 4.16].
$K_X$-negative extremal rays. The proof essentially goes the same way as that of [Reference WatanabeWat21, Proof of Theorem 4.16].
In § 6, we prove Theorem 1.8, which easily follows from the theorems in previous sections.
In the last section, we study the case where ![]() $X$ is
$X$ is ![]() $F$-liftable and prove Theorem 1.12.
$F$-liftable and prove Theorem 1.12.
1.9 Conventions
Throughout this paper, we work over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. We use standard notation and conventions as in [Reference HartshorneHar77], [Reference KollárKol96], [Reference Kollár and MoriKM98], and [Reference DebarreDeb01].
$p>0$. We use standard notation and conventions as in [Reference HartshorneHar77], [Reference KollárKol96], [Reference Kollár and MoriKM98], and [Reference DebarreDeb01].
– Unless otherwise stated, a point means a closed point and a fiber means a fiber over a closed point.
– A rational curve on a variety
 $X$ is a nonconstant morphism
$X$ is a nonconstant morphism  $f \colon \mathbb {P}^1 \to X$ or, by an abuse of notation, its image
$f \colon \mathbb {P}^1 \to X$ or, by an abuse of notation, its image  $f(\mathbb {P}^1) \subset X$.
$f(\mathbb {P}^1) \subset X$.– A contraction
 $f \colon X \to Y$ is a projective morphism of varieties such that
$f \colon X \to Y$ is a projective morphism of varieties such that  $f_* \mathcal {O}_X =\mathcal {O} _Y$.
$f_* \mathcal {O}_X =\mathcal {O} _Y$.– For a contraction
 $f \colon X \to Y$, we denote by
$f \colon X \to Y$, we denote by  $N_1(X / Y)$ the
$N_1(X / Y)$ the  $\mathbb {R}$-vector space of the numerical equivalence classes of relative
$\mathbb {R}$-vector space of the numerical equivalence classes of relative  $1$-cycles. The cone of relative effective
$1$-cycles. The cone of relative effective  $1$-cycles
$1$-cycles  $\operatorname {NE} (X/Y) \subset N_1(X/Y)$ is the semi-subgroup generated by the classes of effective
$\operatorname {NE} (X/Y) \subset N_1(X/Y)$ is the semi-subgroup generated by the classes of effective  $1$-cycles. The closure
$1$-cycles. The closure  $\overline {\operatorname {NE}}(X/Y)$ is called the relative Kleiman–Mori cone.
$\overline {\operatorname {NE}}(X/Y)$ is called the relative Kleiman–Mori cone.– For a contraction
 $X \to Y$, the relative Picard number
$X \to Y$, the relative Picard number  $\rho (X /Y)$ is the rank of
$\rho (X /Y)$ is the rank of  $N_1(X/Y)$.
$N_1(X/Y)$.– For a contraction
 $f \colon X \to Y$,
$f \colon X \to Y$,  $N^1(X/Y)$ is the
$N^1(X/Y)$ is the  $\mathbb {R}$-vector space generated by the
$\mathbb {R}$-vector space generated by the  $f$-numerical equivalence classes of Cartier divisors. Note that
$f$-numerical equivalence classes of Cartier divisors. Note that  $N^1(X/Y)$ and
$N^1(X/Y)$ and  $N_1(X/Y)$ are finite-dimensional vector spaces, which are dual to each other.
$N_1(X/Y)$ are finite-dimensional vector spaces, which are dual to each other.– If
 $Y =\operatorname {Spec} k$, then we will use
$Y =\operatorname {Spec} k$, then we will use  $N_1(X)$,
$N_1(X)$,  $\operatorname {NE}(X)$,
$\operatorname {NE}(X)$,  $\rho (X)$, and
$\rho (X)$, and  $N^1(X)$ instead of
$N^1(X)$ instead of  $N_1(X/Y)$,
$N_1(X/Y)$,  $\operatorname {NE}(X/Y)$,
$\operatorname {NE}(X/Y)$,  $\rho (X/Y)$, and
$\rho (X/Y)$, and  $N^1(X/Y)$.
$N^1(X/Y)$.– For a smooth projective variety
 $S$, a smooth
$S$, a smooth  $S$-fibration is a smooth morphism between varieties whose closed fibers are isomorphic to
$S$-fibration is a smooth morphism between varieties whose closed fibers are isomorphic to  $S$.
$S$.– The dual vector bundle of a vector bundle
 $\mathcal {E}$ is
$\mathcal {E}$ is  $\mathcal {E}^{\vee }$.
$\mathcal {E}^{\vee }$.– The Grothendieck projectivization
 $\operatorname {Proj}(\operatorname {Sym} \mathcal {E})$ of a vector bundle
$\operatorname {Proj}(\operatorname {Sym} \mathcal {E})$ of a vector bundle  $\mathcal {E}$ is
$\mathcal {E}$ is  $\mathbb {P}(\mathcal {E})$.
$\mathbb {P}(\mathcal {E})$.– A subsheaf
 $\mathcal {F} \subset \mathcal {E}$ of a locally free sheaf
$\mathcal {F} \subset \mathcal {E}$ of a locally free sheaf  $\mathcal {E}$ is called a subbundle if the quotient bundle
$\mathcal {E}$ is called a subbundle if the quotient bundle  $\mathcal {E}/\mathcal {F}$ is a locally free sheaf.
$\mathcal {E}/\mathcal {F}$ is a locally free sheaf.– For a projective variety
 $X$, we denote by
$X$, we denote by  $F_X$ the absolute Frobenius morphism
$F_X$ the absolute Frobenius morphism  $X \to X$.
$X \to X$.
Note that a contraction, if it exists, is uniquely determined by ![]() $\operatorname {NE} (X/Y) \subset N_1(X)$. A contraction of a
$\operatorname {NE} (X/Y) \subset N_1(X)$. A contraction of a ![]() $K_X$-negative extremal ray
$K_X$-negative extremal ray ![]() $R$ is, by definition, a contraction
$R$ is, by definition, a contraction ![]() $f \colon X \to Y$ such that
$f \colon X \to Y$ such that ![]() $\rho (X/Y) = 1$ and
$\rho (X/Y) = 1$ and ![]() $R := \operatorname {NE}(X/Y) \subset N_1(X/Y)_{K_X \leq 0}$.
$R := \operatorname {NE}(X/Y) \subset N_1(X/Y)_{K_X \leq 0}$.
Furthermore, we use standard terminology on families of rational curves. For example,
–
 $\operatorname {RatCurves}^{\rm n} (X)$ is (the normalization of) the scheme that parametrizes rational curves on X, and a family of rational curves is an irreducible component
$\operatorname {RatCurves}^{\rm n} (X)$ is (the normalization of) the scheme that parametrizes rational curves on X, and a family of rational curves is an irreducible component  $\mathcal {M}$ of the scheme
$\mathcal {M}$ of the scheme  $\operatorname {RatCurves}^{\rm n} (X)$ (the superscript ‘
$\operatorname {RatCurves}^{\rm n} (X)$ (the superscript ‘ ${\rm n}$’ means that the parameter space is normalized, see [Reference KollárKol96, Chapter II. Definition 2.12]).
${\rm n}$’ means that the parameter space is normalized, see [Reference KollárKol96, Chapter II. Definition 2.12]).– For a family
 $\mathcal {M}$ of rational curves, there exists the diagram
where:
$\mathcal {M}$ of rational curves, there exists the diagram
where:
∗
 $p$ is a smooth
$p$ is a smooth  $\mathbb {P}^1$-fibration, which corresponds to the universal family;
$\mathbb {P}^1$-fibration, which corresponds to the universal family;∗
 $q$ is the evaluation map.
$q$ is the evaluation map.
Thus, a point
 $m \in \mathcal {M}$ corresponds to a rational curve
$m \in \mathcal {M}$ corresponds to a rational curve  $q|_{p^{-1}(m)} \colon p^{-1}(m) \simeq \mathbb {P}^1 \to X$.
$q|_{p^{-1}(m)} \colon p^{-1}(m) \simeq \mathbb {P}^1 \to X$.– A family
 $\mathcal {M}$ of rational curves is called unsplit if it is projective.
$\mathcal {M}$ of rational curves is called unsplit if it is projective.
For the details of the constructions of these spaces and for basic properties, we refer the reader to [Reference KollárKol96, Chapter II, § 2] and also to [Reference MoriMor79].
2. Preliminaries on nef vector bundles
We collect some facts on nef vector bundles.
Let ![]() $\mathcal {E}$ be a vector bundle on a smooth projective variety
$\mathcal {E}$ be a vector bundle on a smooth projective variety ![]() $X$. Then the bundle
$X$. Then the bundle ![]() $\mathcal {E}$ is called nef if the relative tautological divisor
$\mathcal {E}$ is called nef if the relative tautological divisor ![]() $\mathcal {O}_{\mathbb {P}(\mathcal {E})}(1)$ is nef. By the definition, any quotient bundle of a nef vector bundle is again nef. In addition, for a morphism
$\mathcal {O}_{\mathbb {P}(\mathcal {E})}(1)$ is nef. By the definition, any quotient bundle of a nef vector bundle is again nef. In addition, for a morphism ![]() $f \colon Y \to X$ from a projective variety
$f \colon Y \to X$ from a projective variety ![]() $Y$, the pullback
$Y$, the pullback ![]() $f^*\mathcal {E}$ is nef if
$f^*\mathcal {E}$ is nef if ![]() $\mathcal {E}$ is nef, and the converse holds if
$\mathcal {E}$ is nef, and the converse holds if ![]() $f$ is surjective. A vector bundle
$f$ is surjective. A vector bundle ![]() $\mathcal {E}$ is called numerically flat if
$\mathcal {E}$ is called numerically flat if ![]() $\mathcal {E}$ and its dual
$\mathcal {E}$ and its dual ![]() $\mathcal {E}^{\vee }$ are both nef.
$\mathcal {E}^{\vee }$ are both nef.
Note that, by [Reference BartonBar71, Proposition 3.5], the tensor product of two nef vector bundles are nef again. In particular, if ![]() $\mathcal {E}$ is nef, then the exterior products of
$\mathcal {E}$ is nef, then the exterior products of ![]() $\mathcal {E}$ are also nef.
$\mathcal {E}$ are also nef.
By the same argument as in the case of characteristic zero (cf. [Reference LazarsfeldLaz04, Theorem 6.2.12] and [Reference Campana and PeternellCP91, Proposition 1.2]), we have the following.
Proposition 2.1 (Nef vector bundles)
Let ![]() $\mathcal {E}$ be a vector bundle on a smooth projective variety
$\mathcal {E}$ be a vector bundle on a smooth projective variety ![]() $X$. We have the following:
$X$. We have the following:
(1) A vector bundle
 $\mathcal {E}$ is numerically flat if and only if both
$\mathcal {E}$ is numerically flat if and only if both  $\mathcal {E}$ and
$\mathcal {E}$ and  $\det \mathcal {E}^{\vee }$ are nef.
$\det \mathcal {E}^{\vee }$ are nef.(2) Let
 $0 \to \mathcal {F} \to \mathcal {E} \to \mathcal {G} \to 0$ be an exact sequence of vector bundles. Assume that
$0 \to \mathcal {F} \to \mathcal {E} \to \mathcal {G} \to 0$ be an exact sequence of vector bundles. Assume that  $\mathcal {F}$ and
$\mathcal {F}$ and  $\mathcal {G}$ are nef. Then
$\mathcal {G}$ are nef. Then  $\mathcal {E}$ is also nef. Conversely, if
$\mathcal {E}$ is also nef. Conversely, if  $\mathcal {E}$ is nef and
$\mathcal {E}$ is nef and  $c_1(\mathcal {G}) \equiv 0$, then
$c_1(\mathcal {G}) \equiv 0$, then  $\mathcal {F}$ is nef.
$\mathcal {F}$ is nef.(3) Assume
 $\mathcal {E}$ is nef. If
$\mathcal {E}$ is nef. If  $\mathcal {L} \to \mathcal {E}^\vee$ is a non-trivial morphism from a numerically trivial line bundle, then
$\mathcal {L} \to \mathcal {E}^\vee$ is a non-trivial morphism from a numerically trivial line bundle, then  $\mathcal {L}$ defines a subbundle of
$\mathcal {L}$ defines a subbundle of  $\mathcal {E}^\vee$.
$\mathcal {E}^\vee$.
Lemma 2.2 (Numerically flat quotient bundles)
Let ![]() $\mathcal {E}$ be a nef vector bundle on a smooth projective variety, and
$\mathcal {E}$ be a nef vector bundle on a smooth projective variety, and ![]() $\mathcal {Q}$ a torsion free quotient of
$\mathcal {Q}$ a torsion free quotient of ![]() $\mathcal {E}$ such that
$\mathcal {E}$ such that ![]() $c_1(\mathcal {Q}) \equiv 0$. Then
$c_1(\mathcal {Q}) \equiv 0$. Then ![]() $\mathcal {Q}$ is a numerically flat vector bundle. Moreover, the kernel of
$\mathcal {Q}$ is a numerically flat vector bundle. Moreover, the kernel of ![]() $\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.
$\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.
Proof. Consider the dual map ![]() $\mathcal {Q}^{\vee } \to \mathcal {E}^{\vee }$. Then the map
$\mathcal {Q}^{\vee } \to \mathcal {E}^{\vee }$. Then the map ![]() $\det (\mathcal {Q}^{\vee }) \to \bigwedge ^{\operatorname {rank} \mathcal {Q}} \mathcal {E}^\vee$ is a bundle injection by Proposition 2.1(3). Then, by [Reference Demailly, Peternell and SchneiderDPS94, Lemma 1.20], the sheaf
$\det (\mathcal {Q}^{\vee }) \to \bigwedge ^{\operatorname {rank} \mathcal {Q}} \mathcal {E}^\vee$ is a bundle injection by Proposition 2.1(3). Then, by [Reference Demailly, Peternell and SchneiderDPS94, Lemma 1.20], the sheaf ![]() $\mathcal {Q}^{\vee }$ is a subbundle of
$\mathcal {Q}^{\vee }$ is a subbundle of ![]() $\mathcal {E}^{\vee }$. Hence, the composite
$\mathcal {E}^{\vee }$. Hence, the composite ![]() $\mathcal {E} \to \mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is surjective. In particular, the map
$\mathcal {E} \to \mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is surjective. In particular, the map ![]() $\mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is also surjective. Since
$\mathcal {Q} \to \mathcal {Q}^{\vee \vee }$ is also surjective. Since ![]() $\mathcal {Q}$ is torsion free, we have
$\mathcal {Q}$ is torsion free, we have ![]() $\mathcal {Q} = \mathcal {Q}^{\vee \vee }$. Now it follows from Proposition 2.1(2) that the kernel of
$\mathcal {Q} = \mathcal {Q}^{\vee \vee }$. Now it follows from Proposition 2.1(2) that the kernel of ![]() $\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.
$\mathcal {E} \to \mathcal {Q}$ is a nef vector bundle.
Theorem 2.3 [Reference Biswas and Dos SantosBD13]
Let ![]() $X$ be a smooth projective SRC variety and
$X$ be a smooth projective SRC variety and ![]() $\mathcal {E}$ a vector bundle on
$\mathcal {E}$ a vector bundle on ![]() $X$. Assume that, for any rational curve
$X$. Assume that, for any rational curve ![]() $f\colon \mathbb {P}^1 \to X$, the pullback
$f\colon \mathbb {P}^1 \to X$, the pullback ![]() $f^{\ast }\mathcal {E}$ is trivial. Then
$f^{\ast }\mathcal {E}$ is trivial. Then ![]() $\mathcal {E}$ itself is trivial.
$\mathcal {E}$ itself is trivial.
This implies the following.
Corollary 2.4 (see [Reference GounelasGou14])
For a smooth projective SRC variety ![]() $X$, the first cohomology
$X$, the first cohomology ![]() $H^1(X, \mathcal {O}_X)$ vanishes.
$H^1(X, \mathcal {O}_X)$ vanishes.
3. Separable rational connectedness
In this section, we prove Theorem 1.3 and Corollary 1.4.
3.1 Preliminaries: foliations and SRC
Here we collect several results from [Reference ShenShe10], which describe the relation between a variety ![]() $X$ being SRC and foliations on
$X$ being SRC and foliations on ![]() $X$.
$X$.
Let ![]() $X$ be a normal projective variety of dimension
$X$ be a normal projective variety of dimension ![]() $n$. A rational curve
$n$. A rational curve ![]() $f \colon \mathbb {P}^1 \to X$ is called free (respectively, very free) if
$f \colon \mathbb {P}^1 \to X$ is called free (respectively, very free) if ![]() $f(\mathbb {P}^1)$ is contained in the smooth locus of
$f(\mathbb {P}^1)$ is contained in the smooth locus of ![]() $X$, and
$X$, and ![]() $f^*T_X$ is nef (respectively, ample).
$f^*T_X$ is nef (respectively, ample).
Definition 3.1 (RCC, RC, FRC, and SRC; see [Reference KollárKol96, Chapter IV. Definition 3.2] and [Reference ShenShe10, Definition 1.2])
Let ![]() $X$ be a normal projective variety over
$X$ be a normal projective variety over ![]() $k$. Then
$k$. Then ![]() $X$ is called:
$X$ is called:
(1) rationally chain connected (RCC) if there exist a variety
 $T$ and a scheme
$T$ and a scheme  $\mathcal {U}$ with morphisms
$\mathcal {U}$ with morphisms  $(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that
$(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that
–
 $p$-fibers are connected proper curves with only rational components and
$p$-fibers are connected proper curves with only rational components and– the natural map
 $q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;
$q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;
(2) rationally connected (RC) if there exist a variety
 $T$ and a scheme
$T$ and a scheme  $\mathcal {U}$ with morphisms
$\mathcal {U}$ with morphisms  $(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that
$(T \xleftarrow {p} \mathcal {U} \xrightarrow {q} X)$ such that
–
 $p$-fibers are irreducible rational curves and
$p$-fibers are irreducible rational curves and– the natural map
 $q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;
$q^{(2)} \colon \mathcal {U} \times _T \mathcal {U} \to X \times X$ is dominant;
(3) freely rationally connected (FRC) if there exists a variety
 $T$ with morphisms
$T$ with morphisms  $(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that
$(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that
– each
 $\operatorname {pr}_2$-fiber defines a free rational curve on
$\operatorname {pr}_2$-fiber defines a free rational curve on  $X$ and
$X$ and– the natural map
 $q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant;
$q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant;
(4) separably rationally connected (SRC) if there exists a variety
 $T$ with morphisms
$T$ with morphisms  $(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that
$(T \xleftarrow {\operatorname {pr}_2} \mathbb {P}^1 \times T \xrightarrow {q} X)$ such that
– the natural map
 $q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant and smooth at the generic point of
$q^{(2)} \colon \mathbb {P}^1 \times \mathbb {P}^1 \times T \to X \times X$ is dominant and smooth at the generic point of  $\mathbb {P}^1 \times \mathbb {P}^1 \times T$.
$\mathbb {P}^1 \times \mathbb {P}^1 \times T$.
Remark 3.2 (1) Any smooth Fano variety is RCC (see, for instance, [Reference KollárKol96, Chapter V, Theorem 2.13]).
(2) Note that the definition of SRC here is slightly different from the definition in [Reference ShenShe10] (the existence of very free rational curves). However, if ![]() $X$ is smooth, then that
$X$ is smooth, then that ![]() $X$ is SRC is equivalent to the existence of a very free rational curve on
$X$ is SRC is equivalent to the existence of a very free rational curve on ![]() $X$ (see, for instance, [Reference KollárKol96, Chapter IV, Theorem 3.7]). Thus, the two definitions coincide. Note also that, in the situation of this paper, we mainly consider smooth varieties and, thus, we do not need to care about the differences (cf. the smoothness of
$X$ (see, for instance, [Reference KollárKol96, Chapter IV, Theorem 3.7]). Thus, the two definitions coincide. Note also that, in the situation of this paper, we mainly consider smooth varieties and, thus, we do not need to care about the differences (cf. the smoothness of ![]() $X^{[1]}$ in Proposition 3.20).
$X^{[1]}$ in Proposition 3.20).
(3) In general, the following implications hold:
Assume that ![]() $X$ is smooth and
$X$ is smooth and ![]() $T_X$ is nef. Then
$T_X$ is nef. Then ![]() $\text {RCC} \implies \text {FRC}$. This follows from the smoothing technique of free rational curves (see, e.g., [Reference KollárKol96, Chapter II. 7.6]).
$\text {RCC} \implies \text {FRC}$. This follows from the smoothing technique of free rational curves (see, e.g., [Reference KollárKol96, Chapter II. 7.6]).
Assume that a normal projective variety ![]() $X$ contains a free rational curve
$X$ contains a free rational curve ![]() $f \colon \mathbb {P}^1 \to X$. Since any vector bundle on
$f \colon \mathbb {P}^1 \to X$. Since any vector bundle on ![]() $\mathbb {P}^1$ is a direct sum of line bundles, we have
$\mathbb {P}^1$ is a direct sum of line bundles, we have
 \[ f^* T_X \simeq \bigoplus_{i=1}^{r} \mathcal{O}(a_i) \bigoplus \mathcal{O}^{\oplus n-r} \]
\[ f^* T_X \simeq \bigoplus_{i=1}^{r} \mathcal{O}(a_i) \bigoplus \mathcal{O}^{\oplus n-r} \]
with ![]() $a_i >0$.
$a_i >0$.
Definition 3.3 (Positive ranks and maximally free rational curves [Reference ShenShe10, Definition 2.1])
In the above notation, the ample subsheaf ![]() $\bigoplus _{i=1}^{r} \mathcal {O}(a_i)$ defines a subsheaf of
$\bigoplus _{i=1}^{r} \mathcal {O}(a_i)$ defines a subsheaf of ![]() $f^*T_X$ that is independent of the choice of decomposition of
$f^*T_X$ that is independent of the choice of decomposition of ![]() $f^*T_X$.
$f^*T_X$.
(1) This subsheaf
 $\bigoplus _{i=1}^{r} \mathcal {O}(a_i) \subset f^*T_X$ is called the positive part of
$\bigoplus _{i=1}^{r} \mathcal {O}(a_i) \subset f^*T_X$ is called the positive part of  $f^*T_X$, and denoted by
$f^*T_X$, and denoted by  $\operatorname {Pos} (f^*T_X)$.
$\operatorname {Pos} (f^*T_X)$.(2) We call
 $r = \operatorname {rank} \operatorname {Pos} (f^*T_X)$ the positive rank of the free rational curve
$r = \operatorname {rank} \operatorname {Pos} (f^*T_X)$ the positive rank of the free rational curve  $f$.
$f$.(3) The positive rank of
 $X$ is defined as the maximum of positive ranks of the free rational curves.
$X$ is defined as the maximum of positive ranks of the free rational curves.(4) A free rational curve
 $f\colon \mathbb {P}^1 \to X$ is called maximally free if its positive rank is the positive rank of
$f\colon \mathbb {P}^1 \to X$ is called maximally free if its positive rank is the positive rank of  $X$.
$X$.
Proposition 3.4 [Reference ShenShe10, Proposition 2.2]
Let ![]() $x \in X$ be a closed point. Assume that there exists a maximally free rational curve
$x \in X$ be a closed point. Assume that there exists a maximally free rational curve ![]() $f \colon \mathbb {P}^1 \to X$ with
$f \colon \mathbb {P}^1 \to X$ with ![]() $f(\mathbb {P}^1) \ni x$. Then there exists a
$f(\mathbb {P}^1) \ni x$. Then there exists a ![]() $k$-subspace
$k$-subspace ![]() $\mathcal {D} (x) \subset T_X\otimes k(x)$ such that:
$\mathcal {D} (x) \subset T_X\otimes k(x)$ such that:
– for every maximally free rational curve
 $f \colon \mathbb {P}^1 \to X$ with
$f \colon \mathbb {P}^1 \to X$ with  $f(0) = x$, we have
as a subspace of
$f(0) = x$, we have
as a subspace of \[ \operatorname{Pos}(f^*T_X)\otimes k(0) = \mathcal{D} (x) \]
\[ \operatorname{Pos}(f^*T_X)\otimes k(0) = \mathcal{D} (x) \]
 $T_X \otimes k(x)$.
$T_X \otimes k(x)$.
The next proposition ensures that these subspaces ![]() $\mathcal {D} (x)$ patch together to define a subsheaf of
$\mathcal {D} (x)$ patch together to define a subsheaf of ![]() $T_X$.
$T_X$.
Proposition 3.5 [Reference ShenShe10, Proposition 2.5]
There exist a nonempty open subset ![]() $U \subset X$ and a subbundle
$U \subset X$ and a subbundle ![]() $\mathcal {D} \subset T_U$ such that
$\mathcal {D} \subset T_U$ such that
holds for all ![]() $x \in U$.
$x \in U$.
In the following we denote also by ![]() $\mathcal {D} \subset T_X$ the saturation of
$\mathcal {D} \subset T_X$ the saturation of ![]() $\mathcal {D}$ in
$\mathcal {D}$ in ![]() $T_X$ (by an abuse of notation).
$T_X$ (by an abuse of notation).
Theorem 3.6 [Reference ShenShe10, Proposition 2.6]
The sheaf ![]() $\mathcal {D}$ defines a foliation. Namely,
$\mathcal {D}$ defines a foliation. Namely, ![]() $\mathcal {D}$ satisfies the following conditions:
$\mathcal {D}$ satisfies the following conditions:
(1)
 $\mathcal {D}$ is involutive, i.e. it is closed under the Lie bracket
$\mathcal {D}$ is involutive, i.e. it is closed under the Lie bracket  $[\mathcal {D} ,\mathcal {D} ] \subset \mathcal {D}$;
$[\mathcal {D} ,\mathcal {D} ] \subset \mathcal {D}$;(2)
 $\mathcal {D}$ is
$\mathcal {D}$ is  $p$-closed, i.e.
$p$-closed, i.e.  $\mathcal {D} ^p \subset \mathcal {D}$.
$\mathcal {D} ^p \subset \mathcal {D}$.
For the convenience of readers, we briefly recall basic properties of foliations and their quotients. For an account of the general theory of foliations, we refer the reader to [Reference EkedahlEke87, Reference Miyaoka and PeternellMP97].
Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$. Denote by
$k$. Denote by ![]() $\sigma \colon X^{(1)} \to X$ the base change of the absolute Frobenius
$\sigma \colon X^{(1)} \to X$ the base change of the absolute Frobenius ![]() $F_{\operatorname {Spec}(k)}$ on
$F_{\operatorname {Spec}(k)}$ on ![]() $\operatorname {Spec}(k)$ by the structure morphism
$\operatorname {Spec}(k)$ by the structure morphism ![]() $X \to \operatorname {Spec}(k)$ (Note that
$X \to \operatorname {Spec}(k)$ (Note that ![]() $F_{\operatorname {Spec}(k)}$ is an isomorphism). By the definition, the absolute Frobenius morphism
$F_{\operatorname {Spec}(k)}$ is an isomorphism). By the definition, the absolute Frobenius morphism ![]() $F_X \colon X \to X$ factors
$F_X \colon X \to X$ factors ![]() $X^{(1)}$ and we have the relative Frobenius morphism
$X^{(1)}$ and we have the relative Frobenius morphism ![]() $X \to X^{(1)}$ over
$X \to X^{(1)}$ over ![]() $k$. As a scheme, the topological space of
$k$. As a scheme, the topological space of ![]() $X^{(1)}$ is that of
$X^{(1)}$ is that of ![]() $X$, and the structure sheaf is
$X$, and the structure sheaf is ![]() $\mathcal {O}_X^p$. The morphism
$\mathcal {O}_X^p$. The morphism ![]() $X \to X^{(1)}$ corresponds to the inclusion
$X \to X^{(1)}$ corresponds to the inclusion ![]() $\mathcal {O}_X^p \to \mathcal {O}_X$. By the definition of
$\mathcal {O}_X^p \to \mathcal {O}_X$. By the definition of ![]() $\sigma \colon X^{(1)} \to X$, there is a natural identification
$\sigma \colon X^{(1)} \to X$, there is a natural identification ![]() $\sigma ^{*}T_X = T _{X^{(1)}}$.
$\sigma ^{*}T_X = T _{X^{(1)}}$.
A foliation ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $X$ is a saturated subsheaf of
$X$ is a saturated subsheaf of ![]() $T_X$ which is closed under the Lie bracket and
$T_X$ which is closed under the Lie bracket and ![]() $p$-closed. Since
$p$-closed. Since ![]() $T_X$ is the sheaf of derivations
$T_X$ is the sheaf of derivations ![]() $\mathcal {O}_X \to \mathcal {O}_X$, local sections of
$\mathcal {O}_X \to \mathcal {O}_X$, local sections of ![]() $\mathcal {F}$ define local derivations
$\mathcal {F}$ define local derivations ![]() $\mathcal {O}_X \to \mathcal {O}_X$. We denote by
$\mathcal {O}_X \to \mathcal {O}_X$. We denote by ![]() $\operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$ the subsheaf of sections annihilated by
$\operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$ the subsheaf of sections annihilated by ![]() $\mathcal {F}$. By the Leibnitz rule, we have
$\mathcal {F}$. By the Leibnitz rule, we have ![]() $\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F})$. The quotient
$\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F})$. The quotient ![]() $X/\mathcal {F}$ is, by definition, a scheme whose topological space is that of
$X/\mathcal {F}$ is, by definition, a scheme whose topological space is that of ![]() $X$ and structure sheaf
$X$ and structure sheaf ![]() $\operatorname {Ann}(\mathcal {F})$. From the inclusions
$\operatorname {Ann}(\mathcal {F})$. From the inclusions ![]() $\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$, we have morphisms
$\mathcal {O}_X^p \subset \operatorname {Ann}(\mathcal {F}) \subset \mathcal {O}_X$, we have morphisms
such that:
–
 $\sigma \circ g \circ f$ is the absolute Frobenius morphism
$\sigma \circ g \circ f$ is the absolute Frobenius morphism  $F_{X}$;
$F_{X}$;–
 $g \circ f$ is the relative Frobenius morphism over
$g \circ f$ is the relative Frobenius morphism over  $k$.
$k$.
Note that ![]() $f$ and
$f$ and ![]() $g$ are morphisms over
$g$ are morphisms over ![]() $\operatorname {Spec}(k)$, but
$\operatorname {Spec}(k)$, but ![]() $\sigma$ is not. It is known that
$\sigma$ is not. It is known that ![]() $X/\mathcal {F}$ is normal. Moreover, on the open subset where
$X/\mathcal {F}$ is normal. Moreover, on the open subset where ![]() $\mathcal {F}$ is a subbundle of
$\mathcal {F}$ is a subbundle of ![]() $T_X$, the variety
$T_X$, the variety ![]() $X/\mathcal {F}$ is smooth.
$X/\mathcal {F}$ is smooth.
Conversely, if ![]() $Y$ is a normal variety between
$Y$ is a normal variety between ![]() $X$ and
$X$ and ![]() $X^{(1)}$, then there is a foliation
$X^{(1)}$, then there is a foliation ![]() $\mathcal {F}$ such that
$\mathcal {F}$ such that ![]() $Y = X/\mathcal {F}$. This defines a one-to-one correspondence between the set of foliations on
$Y = X/\mathcal {F}$. This defines a one-to-one correspondence between the set of foliations on ![]() $X$ and the set of normal varieties between
$X$ and the set of normal varieties between ![]() $X$ and
$X$ and ![]() $X^{(1)}$.
$X^{(1)}$.
On the open subset where ![]() $\mathcal {F}$ is a subbundle of
$\mathcal {F}$ is a subbundle of ![]() $T_X$, we have the following exact sequence of vector bundles:
$T_X$, we have the following exact sequence of vector bundles:
Namely the foliation ![]() $\mathcal {F}$ is the kernel of the differential map
$\mathcal {F}$ is the kernel of the differential map ![]() $df \colon T_X \to f^* T_{X/\mathcal {F}}$. Note that the last map
$df \colon T_X \to f^* T_{X/\mathcal {F}}$. Note that the last map ![]() $f^*T_{X/\mathcal {F}} \to F_X^* \mathcal {F}$ is induced from the map
$f^*T_{X/\mathcal {F}} \to F_X^* \mathcal {F}$ is induced from the map ![]() $f^*dg \colon f^*T_{X/\mathcal {F}} \to f^*g^*T_{X^{(1)}} = f^*g^*\sigma ^*T_{X} =F_X^*T_X$, i.e.
$f^*dg \colon f^*T_{X/\mathcal {F}} \to f^*g^*T_{X^{(1)}} = f^*g^*\sigma ^*T_{X} =F_X^*T_X$, i.e. ![]() $f^*dg$ factors
$f^*dg$ factors ![]() $F_X^*\mathcal {F} \subset F_X^*T_X$.
$F_X^*\mathcal {F} \subset F_X^*T_X$.
Assume for a moment that ![]() $\mathcal {F}$ is a subbundle of
$\mathcal {F}$ is a subbundle of ![]() $T_X$ and, hence,
$T_X$ and, hence, ![]() $Y := X/\mathcal {F}$ is smooth. By the functoriality, we have the map
$Y := X/\mathcal {F}$ is smooth. By the functoriality, we have the map ![]() $f^{(1)} \colon X^{(1)}\to Y^{(1)}$ and, hence, the variety
$f^{(1)} \colon X^{(1)}\to Y^{(1)}$ and, hence, the variety ![]() $X^{(1)}$ is between
$X^{(1)}$ is between ![]() $Y$ and
$Y$ and ![]() $Y^{(1)}$. Thus,
$Y^{(1)}$. Thus, ![]() $X^{(1)}$ is the quotient
$X^{(1)}$ is the quotient ![]() $Y/\mathcal {G}$ by some foliation
$Y/\mathcal {G}$ by some foliation ![]() $\mathcal {G} \subset T_Y$. On the other hand, by considering the pullback by
$\mathcal {G} \subset T_Y$. On the other hand, by considering the pullback by ![]() $\sigma \circ g$, we obtain a subbundle
$\sigma \circ g$, we obtain a subbundle ![]() $g^* \sigma ^* \mathcal {F} \subset g^* \sigma ^{*}T_X = g^* T _{X^{(1)}}$. For the ease of reference, we include the following.
$g^* \sigma ^* \mathcal {F} \subset g^* \sigma ^{*}T_X = g^* T _{X^{(1)}}$. For the ease of reference, we include the following.
Lemma 3.7 Let the notation be as above. Then the differential map ![]() $dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through
$dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through ![]() $g^* \sigma ^* \mathcal {F}$. The foliation
$g^* \sigma ^* \mathcal {F}$. The foliation ![]() $\mathcal {G}$ is the kernel of the map
$\mathcal {G}$ is the kernel of the map ![]() $T_{Y} \to g^*\sigma ^* \mathcal {F}$. Moreover, we have the following exact sequences:
$T_{Y} \to g^*\sigma ^* \mathcal {F}$. Moreover, we have the following exact sequences:
–
 $0 \to \mathcal {G} \to T_{Y} \to g^*\sigma ^* \mathcal {F} \to 0$;
$0 \to \mathcal {G} \to T_{Y} \to g^*\sigma ^* \mathcal {F} \to 0$;–
 $0 \to \mathcal {F} \to T_X \to f^* T_{Y} \to F_{X}^* \mathcal {F} \to 0$.
$0 \to \mathcal {F} \to T_X \to f^* T_{Y} \to F_{X}^* \mathcal {F} \to 0$.
In particular, ![]() $f^*\mathcal {G} \simeq T_X/\mathcal {F}$.
$f^*\mathcal {G} \simeq T_X/\mathcal {F}$.
Proof. Since ![]() $\mathcal {G}$ corresponds to the quotient
$\mathcal {G}$ corresponds to the quotient ![]() $g \colon Y \to X^{(1)} =Y/\mathcal {G}$, we have the following exact sequence:
$g \colon Y \to X^{(1)} =Y/\mathcal {G}$, we have the following exact sequence:
By pulling back (3.1) by ![]() $\sigma \circ g$, we also have the following exact sequence:
$\sigma \circ g$, we also have the following exact sequence:
Since the composite ![]() $g^*df^{(1)} \circ dg = d(f^{(1)} \circ g)$ is a zero map, the differential
$g^*df^{(1)} \circ dg = d(f^{(1)} \circ g)$ is a zero map, the differential ![]() $dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through
$dg \colon T_{Y} \to g^* T_{X^{(1)}}$ factors through ![]() $g^* \sigma ^* \mathcal {F}$ and, hence,
$g^* \sigma ^* \mathcal {F}$ and, hence, ![]() $\mathcal {G}$ is the kernel of the map
$\mathcal {G}$ is the kernel of the map ![]() $T_{Y} \to g^*\sigma ^* \mathcal {F}$.
$T_{Y} \to g^*\sigma ^* \mathcal {F}$.
On the other hand, since the natural map ![]() $\mathcal {F} \to f^*T_Y$ is a zero map, so is the composite
$\mathcal {F} \to f^*T_Y$ is a zero map, so is the composite ![]() $g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G} \hookrightarrow F_Y^*T_Y =g^*\sigma ^*f^*T_Y$. Thus
$g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G} \hookrightarrow F_Y^*T_Y =g^*\sigma ^*f^*T_Y$. Thus ![]() $g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G}$ is a zero map and, hence, we have the exact sequence
$g^*\sigma ^*\mathcal {F} \xrightarrow {\beta } g^*T_{X^{(1)}} \xrightarrow {\alpha } F_Y^*\mathcal {G}$ is a zero map and, hence, we have the exact sequence
By considering the pullback by ![]() $f$, we have the following exact sequence:
$f$, we have the following exact sequence:
Combining with (3.1), we have ![]() $f^*\mathcal {G} \simeq T_X/\mathcal {F}$.
$f^*\mathcal {G} \simeq T_X/\mathcal {F}$.
Now we return to our situation. There exist the quotient ![]() $X^{[1]} := X/\mathcal {D}$ and a sequence of morphisms
$X^{[1]} := X/\mathcal {D}$ and a sequence of morphisms
In general, ![]() $X^{[1]}$ is normal. In the situation of this paper, however,
$X^{[1]}$ is normal. In the situation of this paper, however, ![]() $\mathcal {D}$ is always a subbundle and, hence,
$\mathcal {D}$ is always a subbundle and, hence, ![]() $X^{[1]}$ is smooth (see Proposition 3.20). The following is Shen's theorem.
$X^{[1]}$ is smooth (see Proposition 3.20). The following is Shen's theorem.
Theorem 3.8 [Reference ShenShe10, Proposition 3.4 and Theorem 5.1]
The following hold:
(1)
 $X$ contains a very free rational curve if and only if
$X$ contains a very free rational curve if and only if  $X^{[1]} \simeq X^{(1)}$;
$X^{[1]} \simeq X^{(1)}$;(2) if
 $X$ is FRC, then so is
$X$ is FRC, then so is  $X^{[1]}$;
$X^{[1]}$;(3) set
 $X^{[m+1]} := (X^{[m]})^{[1]}$ inductively; if
$X^{[m+1]} := (X^{[m]})^{[1]}$ inductively; if  $X$ is FRC, then
$X$ is FRC, then  $X^{[m]}$ contains a very free rational curve for
$X^{[m]}$ contains a very free rational curve for  $m \gg 0$.
$m \gg 0$.
The following is a direct consequence of Lemma 3.7.
Proposition 3.9 (Foliations and tangent bundles)
Assume that ![]() $\mathcal {D}$ is a subbundle of
$\mathcal {D}$ is a subbundle of ![]() $T_X$. Then the differential
$T_X$. Then the differential ![]() $dg \colon T_{X^{[1]}} \to g^* T_{X^{(1)}}$ factors through
$dg \colon T_{X^{[1]}} \to g^* T_{X^{(1)}}$ factors through ![]() $g^* \sigma ^* \mathcal {D}$.
$g^* \sigma ^* \mathcal {D}$.
Denote by ![]() $\mathcal {K}$ the kernel of the map
$\mathcal {K}$ the kernel of the map ![]() $T_{X^{[1]}} \to g^* \sigma ^* \mathcal {D}$. Then
$T_{X^{[1]}} \to g^* \sigma ^* \mathcal {D}$. Then ![]() $\mathcal {K}$ is a foliation on
$\mathcal {K}$ is a foliation on ![]() $X^{[1]}$ and we have
$X^{[1]}$ and we have ![]() $f^* \mathcal {K} \simeq T_X/\mathcal {D}$. Moreover, we have the following exact sequence:
$f^* \mathcal {K} \simeq T_X/\mathcal {D}$. Moreover, we have the following exact sequence:
–
 $0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;
$0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;–
 $0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$.
$0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$.
3.2 Action of group schemes  $\mu _p$ and
$\mu _p$ and  $\alpha _p$
$\alpha _p$
Here we briefly recall the relation between vector fields and actions of group schemes ![]() $\mu _p$ and
$\mu _p$ and ![]() $\alpha _p$. See, e.g., [Reference Demazure and GabrielDG70, Chapitre II, § 7], [Reference Rudakov and ŠafarevičRŠ76, § 1], and [Reference Miyanishi and NomuraMN91, § 1] for an account.
$\alpha _p$. See, e.g., [Reference Demazure and GabrielDG70, Chapitre II, § 7], [Reference Rudakov and ŠafarevičRŠ76, § 1], and [Reference Miyanishi and NomuraMN91, § 1] for an account.
Definition 3.10 ( $\mu _p$ and
$\mu _p$ and  $\alpha _p$)
$\alpha _p$)
The group schemes ![]() $\mu _p$ and
$\mu _p$ and ![]() $\alpha _p$ are defined as follows:
$\alpha _p$ are defined as follows:
–
 $\mu _p := \operatorname {Spec} k[x]/(x^p -1) \subset \mathbb {G}_m = \operatorname {Spec} k[x,x^{-1}]$;
$\mu _p := \operatorname {Spec} k[x]/(x^p -1) \subset \mathbb {G}_m = \operatorname {Spec} k[x,x^{-1}]$;–
 $\alpha _p := \operatorname {Spec} k[x]/(x^p) \subset \mathbb {G}_a = \operatorname {Spec} k[x]$.
$\alpha _p := \operatorname {Spec} k[x]/(x^p) \subset \mathbb {G}_a = \operatorname {Spec} k[x]$.
Here the group scheme structures are induced from ![]() $\mathbb {G}_m$ and
$\mathbb {G}_m$ and ![]() $\mathbb {G}_a$.
$\mathbb {G}_a$.
Proposition 3.11 ( $p$-closed vector fields)
$p$-closed vector fields)
Let ![]() $X$ be a smooth variety and
$X$ be a smooth variety and ![]() $D \in H^0(T_X)$ be a vector field.
$D \in H^0(T_X)$ be a vector field.
(1) There is a one-to-one correspondence between the set of vector fields
 $D$ with
$D$ with  $D^p = D$ and the set of
$D^p = D$ and the set of  $\mu _p$-actions on
$\mu _p$-actions on  $X$.
$X$.(2) There is a one-to-one correspondence between the set of vector fields
 $D$ with
$D$ with  $D^p = 0$ and the set of
$D^p = 0$ and the set of  $\alpha _p$-actions on
$\alpha _p$-actions on  $X$.
$X$.
Remark 3.12 (Quotients by  $\mu _p$ and
$\mu _p$ and  $\alpha _p$)
$\alpha _p$)
Let ![]() $X$ be a smooth projective variety and
$X$ be a smooth projective variety and ![]() $D$ a vector field with
$D$ a vector field with ![]() $D^p = D$ or
$D^p = D$ or ![]() $D^p = 0$. Then there exists the action of
$D^p = 0$. Then there exists the action of ![]() $G = \mu _p$ or
$G = \mu _p$ or ![]() $\alpha _p$ corresponding to
$\alpha _p$ corresponding to ![]() $D$. Then, by [Reference MumfordMum70, § 12, Theorem 1], there exists the quotient
$D$. Then, by [Reference MumfordMum70, § 12, Theorem 1], there exists the quotient ![]() $X/G$. Note that the map
$X/G$. Note that the map ![]() $X \to X/G$ corresponds to the foliation spanned by
$X \to X/G$ corresponds to the foliation spanned by ![]() $D$.
$D$.
Lemma 3.13 (cf. [Reference Rudakov and ŠafarevičRŠ76, § 1 Lemma 1 and Corollary])
Let ![]() $V \subset H^0(T_X)$ be an involutive and
$V \subset H^0(T_X)$ be an involutive and ![]() $p$-closed
$p$-closed ![]() $k$-subspace. Then there exists a vector field
$k$-subspace. Then there exists a vector field ![]() $D \in V$ such that
$D \in V$ such that ![]() $D^p =D$ or
$D^p =D$ or ![]() $D^p = 0$.
$D^p = 0$.
Definition 3.14 (Fixed points)
Set ![]() $G = \mu _p$ or
$G = \mu _p$ or ![]() $\alpha _p$ and consider an action of
$\alpha _p$ and consider an action of ![]() $G$ on a smooth variety
$G$ on a smooth variety ![]() $X$. Let
$X$. Let ![]() $D$ be the corresponding vector field. Then the set of
$D$ be the corresponding vector field. Then the set of ![]() $G$-fixed points is defined as the zero locus of
$G$-fixed points is defined as the zero locus of ![]() $D$.
$D$.
Remark 3.15 A vector field ![]() $D \in H^0 (T_X)$ determines a morphism
$D \in H^0 (T_X)$ determines a morphism ![]() $\varphi _D \colon \mathcal {O} \to T_X$. Then the dual of this map
$\varphi _D \colon \mathcal {O} \to T_X$. Then the dual of this map ![]() $\varphi _D^{\vee } \colon \Omega \to \mathcal {O}_X$ gives a derivation
$\varphi _D^{\vee } \colon \Omega \to \mathcal {O}_X$ gives a derivation ![]() $f_D := \varphi ^{\vee } \circ d$. Since the sheaf
$f_D := \varphi ^{\vee } \circ d$. Since the sheaf ![]() $\Omega _X$ is generated by
$\Omega _X$ is generated by ![]() $d\mathcal {O}_X$ as an
$d\mathcal {O}_X$ as an ![]() $\mathcal {O}_X$-module, the following three subschemes are the same:
$\mathcal {O}_X$-module, the following three subschemes are the same:
(1) the zero locus of
 $D$;
$D$;(2) the closed subscheme whose ideal is
 $\operatorname {Im} (\varphi _D^{\vee })$;
$\operatorname {Im} (\varphi _D^{\vee })$;(3) the closed subscheme whose ideal is generated by
 $\operatorname {Im} (f_D)$.
$\operatorname {Im} (f_D)$.
Lemma 3.16 [Reference Rudakov and ŠafarevičRŠ76, § 1 and Lemma 2]
There exists a ![]() $\mu _p$-action on
$\mu _p$-action on ![]() $\mathbb {P}^1$. Moreover, for any
$\mathbb {P}^1$. Moreover, for any ![]() $\mu _p$-action on
$\mu _p$-action on ![]() $\mathbb {P}^1$, the set of
$\mathbb {P}^1$, the set of ![]() $\mu _p$-fixed points consists of two points.
$\mu _p$-fixed points consists of two points.
Similarly, there exists an ![]() $\alpha _p$-action on
$\alpha _p$-action on ![]() $\mathbb {P}^1$. Moreover, for any
$\mathbb {P}^1$. Moreover, for any ![]() $\alpha _p$-action on
$\alpha _p$-action on ![]() $\mathbb {P}^1$, the support of the set of
$\mathbb {P}^1$, the support of the set of ![]() $\alpha _p$-fixed points consists of one point.
$\alpha _p$-fixed points consists of one point.
Remark 3.17 Since there are only two types of vector fields on ![]() $\mathbb {P}^1$, there are only two kinds of group actions as above (up to isomorphism).
$\mathbb {P}^1$, there are only two kinds of group actions as above (up to isomorphism).
3.3 Proof of Theorem 1.3
Throughout this subsection, we assume that:
–
 $X$ is a smooth projective variety with nef tangent bundle and moreover
$X$ is a smooth projective variety with nef tangent bundle and moreover  $X$ is RCC.
$X$ is RCC.
Lemma 3.18 The vector space ![]() $N_1(X)$ is spanned by maximally free rational curves.
$N_1(X)$ is spanned by maximally free rational curves.
Proof. It is enough to show that, if a divisor ![]() $H$ is not numerically trivial, then
$H$ is not numerically trivial, then ![]() $H \cdot C \neq 0$ for some maximally free rational curve
$H \cdot C \neq 0$ for some maximally free rational curve ![]() $C$.
$C$.
Note that, by [Reference KollárKol96, Chapter IV, Theorem 3.13], ![]() $N_1 (X)$ is generated by rational curves. Assume
$N_1 (X)$ is generated by rational curves. Assume ![]() $H \not \equiv 0$. Then there exists a rational curve
$H \not \equiv 0$. Then there exists a rational curve ![]() $g \colon \mathbb {P}^1 \to D := g(\mathbb {P}^1) \subset X$ such that
$g \colon \mathbb {P}^1 \to D := g(\mathbb {P}^1) \subset X$ such that ![]() $H \cdot D \neq 0$. Since the tangent bundle is nef, the curve
$H \cdot D \neq 0$. Since the tangent bundle is nef, the curve ![]() $D$ is free.
$D$ is free.
Let ![]() $f \colon \mathbb {P}^1 \to C := f(\mathbb {P}^1) \subset X$ be a maximally free rational curve. Since
$f \colon \mathbb {P}^1 \to C := f(\mathbb {P}^1) \subset X$ be a maximally free rational curve. Since ![]() $C$ and
$C$ and ![]() $D$ are both free rational curves, deformations of these curves cover open subsets of
$D$ are both free rational curves, deformations of these curves cover open subsets of ![]() $X$ and, hence, we may assume that
$X$ and, hence, we may assume that ![]() $C \cap D \neq \emptyset$. Then, by [Reference KollárKol96, Chapter II, Theorem 7.6], there is a smoothing
$C \cap D \neq \emptyset$. Then, by [Reference KollárKol96, Chapter II, Theorem 7.6], there is a smoothing ![]() $C'$ of
$C'$ of ![]() $C \cup D$.
$C \cup D$.
Claim 3.19 We claim that ![]() $C'$ is a maximally free rational curve.
$C'$ is a maximally free rational curve.
Proof of Claim 3.19 Let ![]() $f ' \colon \mathbb {P}^1 \to C' \subset X$ be the normalization of
$f ' \colon \mathbb {P}^1 \to C' \subset X$ be the normalization of ![]() $C'$, and
$C'$, and ![]() $h \colon Z \to C \cup D \subset X$ a map from the tree of two rational curves to
$h \colon Z \to C \cup D \subset X$ a map from the tree of two rational curves to ![]() $C\cup D$. Then, by the semicontinuity, we have
$C\cup D$. Then, by the semicontinuity, we have
Let ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ be the irreducible components of
$Z_2$ be the irreducible components of ![]() $Z$, each of which is isomorphic to
$Z$, each of which is isomorphic to ![]() $\mathbb {P}^1$, and
$\mathbb {P}^1$, and ![]() $p \in Z_1 \cap Z_2$ be the intersection point. We may assume
$p \in Z_1 \cap Z_2$ be the intersection point. We may assume ![]() $h|_{Z_1} = f$ and
$h|_{Z_1} = f$ and ![]() $h|_{Z_2} = g$. Then we have the following exact sequence:
$h|_{Z_2} = g$. Then we have the following exact sequence:
Since ![]() $T_X$ is nef, we have
$T_X$ is nef, we have ![]() $H^0 (g^*\Omega _X (-p)) =0$ and, hence,
$H^0 (g^*\Omega _X (-p)) =0$ and, hence, ![]() $h^0 (h^*\Omega _X) \leq h^0 (f^*\Omega _X)$. Thus, we have
$h^0 (h^*\Omega _X) \leq h^0 (f^*\Omega _X)$. Thus, we have ![]() $h^0 (f'^*\Omega _X) \leq h^0 (f^*\Omega _X)$ and have
$h^0 (f'^*\Omega _X) \leq h^0 (f^*\Omega _X)$ and have
Since ![]() $f \colon \mathbb {P}^1 \to X$ is maximally free, so is
$f \colon \mathbb {P}^1 \to X$ is maximally free, so is ![]() $f'$.
$f'$.
Now, we have ![]() $H \cdot C' = H\cdot C + H \cdot D \neq 0$, and the assertion follows.
$H \cdot C' = H\cdot C + H \cdot D \neq 0$, and the assertion follows.
Proposition 3.20 (Purely inseparable modification)
The quotient ![]() $X^{[1]}$ is also a smooth, RCC, projective variety with nef tangent bundle. Moreover, if
$X^{[1]}$ is also a smooth, RCC, projective variety with nef tangent bundle. Moreover, if ![]() $X$ is not SRC, then the subsheaf
$X$ is not SRC, then the subsheaf ![]() $\mathcal {K} \subset T_{X^{[1]}}$ is a numerically flat non-zero subbundle.
$\mathcal {K} \subset T_{X^{[1]}}$ is a numerically flat non-zero subbundle.
Proof. Consider the exact sequence
By definition, ![]() $T_X/\mathcal {D}$ is trivial on the maximally free rational curves. Note that, since
$T_X/\mathcal {D}$ is trivial on the maximally free rational curves. Note that, since ![]() $T_X$ is nef, any rational curve
$T_X$ is nef, any rational curve ![]() $C$ is free and, hence, it admits a deformation
$C$ is free and, hence, it admits a deformation ![]() $C'$ such that
$C'$ such that ![]() $T_X/\mathcal {D}$ is locally free on
$T_X/\mathcal {D}$ is locally free on ![]() $C'$ [Reference KollárKol96, Chapter II. Proposition 3.7]. In particular,
$C'$ [Reference KollárKol96, Chapter II. Proposition 3.7]. In particular, ![]() $c_1(T_X/\mathcal {D} )$ is nef on any rational curve (since
$c_1(T_X/\mathcal {D} )$ is nef on any rational curve (since ![]() $T_X$ is nef and locally free quotients of nef vector bundles are again nef). By the previous lemma, we have
$T_X$ is nef and locally free quotients of nef vector bundles are again nef). By the previous lemma, we have ![]() $c_1(T_X/\mathcal {D} ) \equiv 0$. Then, by Lemma 2.2,
$c_1(T_X/\mathcal {D} ) \equiv 0$. Then, by Lemma 2.2, ![]() $T_X/\mathcal {D}$ is a numerically flat vector bundle. In particular,
$T_X/\mathcal {D}$ is a numerically flat vector bundle. In particular, ![]() $X^{[1]}$ is also smooth. Note that
$X^{[1]}$ is also smooth. Note that ![]() $\mathcal {D}$ is nef by Lemma 2.2.
$\mathcal {D}$ is nef by Lemma 2.2.
Recall that there are the following exact sequences:
–
 $0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;
$0 \to \mathcal {K} \to T_{X^{[1]}} \to g^*\sigma ^* \mathcal {D} \to 0$;–
 $0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$;
$0 \to \mathcal {D} \to T_X \to f^* T_{X^{[1]}} \to F_{X}^* \mathcal {D} \to 0$;
and that ![]() $f^* \mathcal {K} = T_X/\mathcal {D}$. In particular,
$f^* \mathcal {K} = T_X/\mathcal {D}$. In particular, ![]() $\mathcal {K}$ is a numerically flat vector bundle. Note that, if
$\mathcal {K}$ is a numerically flat vector bundle. Note that, if ![]() $\mathcal {K}=0$, then
$\mathcal {K}=0$, then ![]() $\mathcal {D} = T_X$. In this case,
$\mathcal {D} = T_X$. In this case, ![]() $X^{[1]} \simeq X^{(1)}$ and, thus,
$X^{[1]} \simeq X^{(1)}$ and, thus, ![]() $X$ is SRC. This shows that
$X$ is SRC. This shows that ![]() $\mathcal {K}$ is non-zero if
$\mathcal {K}$ is non-zero if ![]() $X$ is not SRC.
$X$ is not SRC.
Since ![]() $\mathcal {D}$ is nef, so is
$\mathcal {D}$ is nef, so is ![]() $F_{X}^*\mathcal {D}$. Hence,
$F_{X}^*\mathcal {D}$. Hence, ![]() $f^* T_{X^{[1]}}$ is also nef. In particular,
$f^* T_{X^{[1]}}$ is also nef. In particular, ![]() $T_{X^{[1]}}$ is nef.
$T_{X^{[1]}}$ is nef.
Since ![]() $X$ is RCC, so is
$X$ is RCC, so is ![]() $X^{[1]}$.
$X^{[1]}$.
Corollary 3.21 (Purely inseparable modification and vector fields)
Assume that ![]() $X$ is not SRC. Then there exists a positive integer
$X$ is not SRC. Then there exists a positive integer ![]() $m>0$ such that
$m>0$ such that ![]() $X^{[m]}$ is SRC and
$X^{[m]}$ is SRC and ![]() $T_{X^{[m]}}$ is nef. Moreover,
$T_{X^{[m]}}$ is nef. Moreover, ![]() $T_{X^{[m]}}$ contains an involutive,
$T_{X^{[m]}}$ contains an involutive, ![]() $p$-closed trivial subbundle
$p$-closed trivial subbundle ![]() $\bigoplus \mathcal {O}$.
$\bigoplus \mathcal {O}$.
In particular, there exists a nowhere vanishing vector field ![]() $D$ such that
$D$ such that ![]() $D ^p=D$ or
$D ^p=D$ or ![]() $D^p=0$.
$D^p=0$.
Proof. By Proposition 3.20, ![]() $X^{[i]}$ are all smooth, RCC, projective variety with nef tangent bundle. Note that, for smooth projective varieties, being SRC is equivalent to the existence of very free rational curves.
$X^{[i]}$ are all smooth, RCC, projective variety with nef tangent bundle. Note that, for smooth projective varieties, being SRC is equivalent to the existence of very free rational curves.
By Theorem 3.8, there exists an integer ![]() $m>0$ such that
$m>0$ such that ![]() $X^{[m]}$ is SRC. Since
$X^{[m]}$ is SRC. Since ![]() $X$ is not SRC, we may choose
$X$ is not SRC, we may choose ![]() $m$ such that
$m$ such that ![]() $X^{[m-1]}$ is not SRC but
$X^{[m-1]}$ is not SRC but ![]() $X^{[m]}$ is SRC. Applying Proposition 3.20 to
$X^{[m]}$ is SRC. Applying Proposition 3.20 to ![]() $X^{[m-1]}$, we see that
$X^{[m-1]}$, we see that ![]() $T_{X^{[m]}}$ contains a numerically flat non-zero subbundle
$T_{X^{[m]}}$ contains a numerically flat non-zero subbundle ![]() $\mathcal {K}$. By Proposition 2.3,
$\mathcal {K}$. By Proposition 2.3, ![]() $\mathcal {K}$ is trivial. In addition, by Proposition 3.9,
$\mathcal {K}$ is trivial. In addition, by Proposition 3.9, ![]() $\mathcal {K}$ is
$\mathcal {K}$ is ![]() $p$-closed and involutive. The last assertion follows from Lemma 3.13.
$p$-closed and involutive. The last assertion follows from Lemma 3.13.
The above corollary yields a contradiction to the following proposition.
Proposition 3.22 (Fixed points on SRC varieties)
Let ![]() $X$ be a smooth SRC variety. Then any vector field
$X$ be a smooth SRC variety. Then any vector field ![]() $D$ with
$D$ with ![]() $D^p =D$ or
$D^p =D$ or ![]() $D^p=0$ admits a zero point.
$D^p=0$ admits a zero point.
Proof. The proof proceeds as Kollár's proof of simple connectedness of SRC varieties (cf. [Reference DebarreDeb03, Corollaire 3.6]).
There is an action of ![]() $G = \mu _p$ or
$G = \mu _p$ or ![]() $\alpha _p$ that corresponds to
$\alpha _p$ that corresponds to ![]() $D$. Fix an action of
$D$. Fix an action of ![]() $G$ onto
$G$ onto ![]() $\mathbb {P}^1$. Note that the set of
$\mathbb {P}^1$. Note that the set of ![]() $G$-fixed points on
$G$-fixed points on ![]() $\mathbb {P}^1$ is not empty.
$\mathbb {P}^1$ is not empty.
Consider the action of ![]() $G$ on
$G$ on ![]() $X \times \mathbb {P}^1$ and the quotient
$X \times \mathbb {P}^1$ and the quotient ![]() $(X \times \mathbb {P}^1)/G$. Then we have the following commutative diagram.
$(X \times \mathbb {P}^1)/G$. Then we have the following commutative diagram.

Note that, on the open subsets where ![]() $G$ acts freely, the above diagram is given by a fiber product and, hence, the general
$G$ acts freely, the above diagram is given by a fiber product and, hence, the general ![]() $\pi$-fiber is isomorphic to
$\pi$-fiber is isomorphic to ![]() $X$. Since the general
$X$. Since the general ![]() $\pi$-fiber is isomorphic to a SRC variety
$\pi$-fiber is isomorphic to a SRC variety ![]() $X$,
$X$, ![]() $\pi$ admits a section
$\pi$ admits a section ![]() $t \colon \mathbb {P}^1 \to (X\times \mathbb {P}^1)/G$ [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03].
$t \colon \mathbb {P}^1 \to (X\times \mathbb {P}^1)/G$ [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03].
Then the pullback of this section by ![]() $\psi$ gives a
$\psi$ gives a ![]() $G$-equivariant section
$G$-equivariant section ![]() $s \colon \mathbb {P}^1 \to X \times \mathbb {P}^1$ of
$s \colon \mathbb {P}^1 \to X \times \mathbb {P}^1$ of ![]() $\operatorname {pr}_2$. Hence,
$\operatorname {pr}_2$. Hence, ![]() $\operatorname {pr}_1 \circ s$ is also
$\operatorname {pr}_1 \circ s$ is also ![]() $G$-equivariant. Therefore, we have a
$G$-equivariant. Therefore, we have a ![]() $G$-equivariant morphism
$G$-equivariant morphism ![]() $\mathbb {P}^1 \to X$. Since any
$\mathbb {P}^1 \to X$. Since any ![]() $G$-action on
$G$-action on ![]() $\mathbb {P}^1$ admits a
$\mathbb {P}^1$ admits a ![]() $G$-fixed point, there exists a
$G$-fixed point, there exists a ![]() $G$-fixed point on
$G$-fixed point on ![]() $X$.
$X$.
Proof of Corollary 1.4 The first assertion follows from a theorem of Kollár [Reference DebarreDeb03, Corollaire 3.6] or [Reference ShenShe10, Corollary 5.3]. The second assertion follows from Corollary 2.4. The last assertion follows from Theorem 2.3.
4. Existence and smoothness of extremal contractions
In this section, we will prove Theorem 1.5. Throughout this section:
–
 $X$ is a smooth projective variety over
$X$ is a smooth projective variety over  $k$, and the tangent bundle
$k$, and the tangent bundle  $T_X$ is nef.
$T_X$ is nef.
We divide the proof into several steps.
Lemma 4.1 Let ![]() $M \to N$ be a finite étale Galois morphism between smooth projective varieties over
$M \to N$ be a finite étale Galois morphism between smooth projective varieties over ![]() $k$ and
$k$ and ![]() $G$ its Galois group. Assume that
$G$ its Galois group. Assume that ![]() $M$ admits a
$M$ admits a ![]() $G$-equivariant contraction
$G$-equivariant contraction ![]() $f \colon M \to S$. Then there exist a normal projective variety
$f \colon M \to S$. Then there exist a normal projective variety ![]() $T$, a finite morphism
$T$, a finite morphism ![]() $S \to T$ and a contraction
$S \to T$ and a contraction ![]() $g \colon N \to T$ such that the following diagram commutes.
$g \colon N \to T$ such that the following diagram commutes.

In particular, if ![]() $f$ is smooth, then any fiber of
$f$ is smooth, then any fiber of ![]() $g$ is irreducible and is the image of an
$g$ is irreducible and is the image of an ![]() $f$-fiber.
$f$-fiber.
Proof. Consider the quotient map ![]() $S \to S/G$. Then there exists a morphism
$S \to S/G$. Then there exists a morphism ![]() $N \to S/G$ since
$N \to S/G$ since ![]() $N = M/G$. Let
$N = M/G$. Let ![]() $N \to T \to S/G$ be the Stein factorization of the map
$N \to T \to S/G$ be the Stein factorization of the map ![]() $N \to S/G$. Then, by the rigidity lemma [Reference DebarreDeb01, Lemma 1.15], there exists a morphism
$N \to S/G$. Then, by the rigidity lemma [Reference DebarreDeb01, Lemma 1.15], there exists a morphism ![]() $S \to T$ as desired.
$S \to T$ as desired.
In the following we consider a diagram of the following form:

where ![]() $p$ is a smooth
$p$ is a smooth ![]() $\mathbb {P}^1$-fibration,
$\mathbb {P}^1$-fibration, ![]() $\mathcal {U}$ and
$\mathcal {U}$ and ![]() $\mathcal {M}$ are projective varieties, and any
$\mathcal {M}$ are projective varieties, and any ![]() $p$-fiber is not contracted to a point by
$p$-fiber is not contracted to a point by ![]() $q$. Two closed points
$q$. Two closed points ![]() $x$,
$x$, ![]() $y \in X$ are said to be
$y \in X$ are said to be ![]() $\mathcal {M}$-equivalent if there exists a connected chain of rational curves parametrized by
$\mathcal {M}$-equivalent if there exists a connected chain of rational curves parametrized by ![]() $\mathcal {M}$ which contains both
$\mathcal {M}$ which contains both ![]() $x$ and
$x$ and ![]() $y$. Given a set
$y$. Given a set ![]() $\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ of diagrams as above, we similarly define the
$\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ of diagrams as above, we similarly define the ![]() $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence relation as follows: two closed points
$(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence relation as follows: two closed points ![]() $x$,
$x$, ![]() $y \in X$ are said to be
$y \in X$ are said to be ![]() $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalent if there exists a connected chain of rational curves parametrized by
$(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalent if there exists a connected chain of rational curves parametrized by ![]() $\mathcal {M}_1 \cup \cdots \cup \mathcal {M}_m$ which contains both
$\mathcal {M}_1 \cup \cdots \cup \mathcal {M}_m$ which contains both ![]() $x$ and
$x$ and ![]() $y$.
$y$.
Recall that a family of rational curves is called unsplit if the family ![]() $\mathcal {M}$ is projective. For the ease of reference, we include some properties of unsplit family of rational curves on varieties with nef tangent bundles.
$\mathcal {M}$ is projective. For the ease of reference, we include some properties of unsplit family of rational curves on varieties with nef tangent bundles.
Lemma 4.2 [Reference KollárKol96, Chapter II, Theorem 1.7, Proposition 2.14.1, Theorem 2.15, and Corollary 3.5.3]
An unsplit family of rational curves gives a diagram as (4.1). In this case, ![]() $q$ is a smooth morphism. Moreover,
$q$ is a smooth morphism. Moreover, ![]() $\mathcal {U}$ and
$\mathcal {U}$ and ![]() $\mathcal {M}$ are smooth projective varieties.
$\mathcal {M}$ are smooth projective varieties.
Proposition 4.3 (Existence of contractions)
Let ![]() $C$ be a curve parametrized by
$C$ be a curve parametrized by ![]() $\mathcal {M}$ and set
$\mathcal {M}$ and set ![]() $R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$. If
$R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$. If ![]() $q$ is equidimensional with irreducible fibers, then
$q$ is equidimensional with irreducible fibers, then ![]() $R$ is an extremal ray and there exists a contraction of
$R$ is an extremal ray and there exists a contraction of ![]() $R$.
$R$.
Moreover, the contraction is equidimensional with irreducible fibers, each fiber ![]() $F$ of the contraction (with its reduced structure) is an
$F$ of the contraction (with its reduced structure) is an ![]() $\mathcal {M}$-equivalent class, and
$\mathcal {M}$-equivalent class, and ![]() $\rho (F) = 1$.
$\rho (F) = 1$.
Proof. By [Reference KanemitsuKan22, Theorem 2.2], we obtain a projective morphism ![]() $f \colon X \to Y$ onto a projective normal variety
$f \colon X \to Y$ onto a projective normal variety ![]() $Y$ such that each fiber is an
$Y$ such that each fiber is an ![]() $\mathcal {M}$-equivalent class; moreover,
$\mathcal {M}$-equivalent class; moreover, ![]() $f$ is equidimensional with irreducible fibers. Note that the proof of [Reference KanemitsuKan22, Theorem 2.2] works also in positive characteristic. Let
$f$ is equidimensional with irreducible fibers. Note that the proof of [Reference KanemitsuKan22, Theorem 2.2] works also in positive characteristic. Let ![]() $F$ be a fiber of
$F$ be a fiber of ![]() $f$. Then, by [Reference KollárKol96, Chapter IV, Proposition 3.13.3], the group of rational equivalence classes of algebraic
$f$. Then, by [Reference KollárKol96, Chapter IV, Proposition 3.13.3], the group of rational equivalence classes of algebraic ![]() $1$-cycles with rational coefficients
$1$-cycles with rational coefficients ![]() $A_1(F)_{\mathbb {Q}}$ is generated by curves in
$A_1(F)_{\mathbb {Q}}$ is generated by curves in ![]() $\mathcal {M}$. Let
$\mathcal {M}$. Let ![]() $\mathcal {M}_F := p(q^{-1}(F))$ be the closed subset parametrizing
$\mathcal {M}_F := p(q^{-1}(F))$ be the closed subset parametrizing ![]() $1$-cycles contained in
$1$-cycles contained in ![]() $F$. Then the facts that
$F$. Then the facts that ![]() $F$ is an
$F$ is an ![]() $\mathcal {M}$-equivalent class and that
$\mathcal {M}$-equivalent class and that ![]() $q$-fibers are connected imply that
$q$-fibers are connected imply that ![]() $\mathcal {M}_F$ is connected. Thus,
$\mathcal {M}_F$ is connected. Thus, ![]() $N_1(F) \simeq \mathbb {R}$. In particular,
$N_1(F) \simeq \mathbb {R}$. In particular, ![]() $R$ is an extremal ray and
$R$ is an extremal ray and ![]() $f$ is the contraction of
$f$ is the contraction of ![]() $R$.
$R$.
The following is an adaption of [Reference KollárKol96, Chapter I. Theorem 6.5] in a form that we need along the proof.
Theorem 4.4 [Reference KollárKol96, Chapter I. Theorem 6.5]
Let ![]() $M$,
$M$, ![]() $N$ be two varieties over
$N$ be two varieties over ![]() $k$, and let
$k$, and let ![]() $h \colon M \to N$ be a proper morphism. Assume that:
$h \colon M \to N$ be a proper morphism. Assume that:
–
 $N$ is normal;
$N$ is normal;–
 $h$ is equidimensional with irreducible fibers.
$h$ is equidimensional with irreducible fibers.
Then ![]() $M \to N$ is a well-defined family of algebraic cycles in the sense of [Reference KollárKol96, Chapter I].
$M \to N$ is a well-defined family of algebraic cycles in the sense of [Reference KollárKol96, Chapter I].
Fix a point ![]() $m \in M$ and let
$m \in M$ and let ![]() $F := h^{-1}(h(m))$ be the scheme-theoretic fiber. Assume further that:
$F := h^{-1}(h(m))$ be the scheme-theoretic fiber. Assume further that:
(1)
 $F$ is generically reduced;
$F$ is generically reduced;(2) the reduced scheme
 $F_{\mathrm {red}}$ associated to
$F_{\mathrm {red}}$ associated to  $F$ is smooth at
$F$ is smooth at  $m$.
$m$.
Then ![]() $h$ is smooth at
$h$ is smooth at ![]() $m \in M$.
$m \in M$.
Proof. The assertion that ![]() $M \to N$ is a well-defined family of algebraic cycles follows from [Reference KollárKol96, Chapter I, Theorem 3.17]. If condition (1) holds, then the cycle-theoretic fiber
$M \to N$ is a well-defined family of algebraic cycles follows from [Reference KollárKol96, Chapter I, Theorem 3.17]. If condition (1) holds, then the cycle-theoretic fiber ![]() $h^{[-1]}(h(m))$ is the cycle
$h^{[-1]}(h(m))$ is the cycle ![]() $F_\mathrm {red}$. Then condition (2) and [Reference KollárKol96, Chapter I, Theorem 6.5] imply that
$F_\mathrm {red}$. Then condition (2) and [Reference KollárKol96, Chapter I, Theorem 6.5] imply that ![]() $h$ is smooth at
$h$ is smooth at ![]() $m$.
$m$.
Proposition 4.5 (Smoothness of contractions)
Let ![]() $C$ be a curve parametrized by
$C$ be a curve parametrized by ![]() $\mathcal {M}$ and set
$\mathcal {M}$ and set ![]() $R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$.
$R := \mathbb {R}_{\geq 0} [C] \subset \overline {\operatorname {NE}}(X)$.
Assume that ![]() $R$ is extremal and the contraction
$R$ is extremal and the contraction ![]() $f \colon X \to Y$ of
$f \colon X \to Y$ of ![]() $R$ exists. Assume, moreover, that:
$R$ exists. Assume, moreover, that:
–
 $q$ is smooth;
$q$ is smooth;–
 $f$ is equidimensional with irreducible fibers;
$f$ is equidimensional with irreducible fibers;– every
 $f$-fiber is an
$f$-fiber is an  $\mathcal {M}$-equivalent class.
$\mathcal {M}$-equivalent class.
Then the following hold:
(1)
 $f$ is smooth;
$f$ is smooth;(2) every fiber
 $F$ of
$F$ of  $f$ is an SRC Fano variety with nef tangent bundle;
$f$ is an SRC Fano variety with nef tangent bundle;(3)
 $T_Y$ is again nef.
$T_Y$ is again nef.
Proof. Let ![]() $F$ be a scheme-theoretic fiber of
$F$ be a scheme-theoretic fiber of ![]() $f$ and
$f$ and ![]() $F_\mathrm {red}$ the reduced scheme associated to
$F_\mathrm {red}$ the reduced scheme associated to ![]() $F$.
$F$.
Step 1 In this step, we show that ![]() $F_\mathrm {red}$ is a smooth SRC Fano variety with nef tangent bundle and that the Hilbert scheme of
$F_\mathrm {red}$ is a smooth SRC Fano variety with nef tangent bundle and that the Hilbert scheme of ![]() $X$ is smooth of dimension
$X$ is smooth of dimension ![]() $\dim Y$ at
$\dim Y$ at ![]() $F_\mathrm {red}$.
$F_\mathrm {red}$.
Note that ![]() $F_{\mathrm {red}}$ is an
$F_{\mathrm {red}}$ is an ![]() $\mathcal {M}$-equivalent class. By the same argument as in [Reference Solá Conde and WiśniewskiSW04, Lemma 4.12], one can show that
$\mathcal {M}$-equivalent class. By the same argument as in [Reference Solá Conde and WiśniewskiSW04, Lemma 4.12], one can show that ![]() $F_{\mathrm {red}}$ is smooth, and the normal bundle
$F_{\mathrm {red}}$ is smooth, and the normal bundle ![]() $N_{F_{\mathrm {red}}/X}$ is numerically flat. Consider the standard exact sequence
$N_{F_{\mathrm {red}}/X}$ is numerically flat. Consider the standard exact sequence
Combining this sequence with Proposition 2.1(2), we see that the tangent bundle ![]() $T_{F_{\mathrm {red}}}$ is nef. In addition, by adjunction,
$T_{F_{\mathrm {red}}}$ is nef. In addition, by adjunction, ![]() $-K_{F_{\mathrm {red}}} \equiv -K_X|_{F_{\mathrm {red}}}$. Thus,
$-K_{F_{\mathrm {red}}} \equiv -K_X|_{F_{\mathrm {red}}}$. Thus, ![]() $F_{\mathrm {red}}$ is a smooth Fano variety with nef tangent bundle. Then Theorem 1.3 implies that
$F_{\mathrm {red}}$ is a smooth Fano variety with nef tangent bundle. Then Theorem 1.3 implies that ![]() $F_{\mathrm {red}}$ is SRC. Applying Theorem 2.3 and Corollary 2.4, we see that
$F_{\mathrm {red}}$ is SRC. Applying Theorem 2.3 and Corollary 2.4, we see that ![]() $N_{F_{\mathrm {red}}/X}$ is trivial and
$N_{F_{\mathrm {red}}/X}$ is trivial and ![]() $H^1(F_{\mathrm {red}},\mathcal {O}_{F_{\mathrm {red}}})=0$. In particular, the Hilbert scheme is smooth of dimension
$H^1(F_{\mathrm {red}},\mathcal {O}_{F_{\mathrm {red}}})=0$. In particular, the Hilbert scheme is smooth of dimension ![]() $\dim Y$ at
$\dim Y$ at ![]() $[F_{\mathrm {red}}]$.
$[F_{\mathrm {red}}]$.
Step 2 Here we reduce to prove that some fiber of ![]() $f$ is generically reduced. Assume for a moment that some fiber of
$f$ is generically reduced. Assume for a moment that some fiber of ![]() $f$ is generically reduced. Then, since
$f$ is generically reduced. Then, since ![]() $F_{\mathrm {red}}$ is unobstructed, it is numerically equivalent to a general fiber which is generically reduced by the assumption. This is possible if and only if
$F_{\mathrm {red}}$ is unobstructed, it is numerically equivalent to a general fiber which is generically reduced by the assumption. This is possible if and only if ![]() $F$ is generically reduced. By Theorem 4.4,
$F$ is generically reduced. By Theorem 4.4, ![]() $f$ is smooth. Finally,
$f$ is smooth. Finally, ![]() $T_Y$ is nef by Proposition 2.1. Thus it is enough to prove that some fiber of
$T_Y$ is nef by Proposition 2.1. Thus it is enough to prove that some fiber of ![]() $f$ is generically reduced.
$f$ is generically reduced.
Step 3 Let ![]() $X_2 = X$ be a copy of
$X_2 = X$ be a copy of ![]() $X$ and denote by
$X$ and denote by ![]() $X_1$ the original variety
$X_1$ the original variety ![]() $X$. Let
$X$. Let ![]() $V \subset X \times X$ be the graph of the
$V \subset X \times X$ be the graph of the ![]() $\mathcal {M}$-equivalence relation (with its reduced scheme structure). We will denote by
$\mathcal {M}$-equivalence relation (with its reduced scheme structure). We will denote by ![]() $p_1 \colon V \to X_1$ and
$p_1 \colon V \to X_1$ and ![]() $p_2 \colon V \to X_2$ the natural projections. In this step, we show that the geometric generic fiber of
$p_2 \colon V \to X_2$ the natural projections. In this step, we show that the geometric generic fiber of ![]() $p_2 \colon V \to X_2$ is reduced. We follow the proof of [Reference StarrSta06, Lemma 2.3].
$p_2 \colon V \to X_2$ is reduced. We follow the proof of [Reference StarrSta06, Lemma 2.3].
By taking products with ![]() $X_2$, we have the following diagram.
$X_2$, we have the following diagram.

Set ![]() $V_0 := \Delta \subset X_1 \times X_2$ (the diagonal) and
$V_0 := \Delta \subset X_1 \times X_2$ (the diagonal) and ![]() $V_{i+1} := Q(P^{-1}(P(Q^{-1}(V_{i}))))$ inductively. Then, for
$V_{i+1} := Q(P^{-1}(P(Q^{-1}(V_{i}))))$ inductively. Then, for ![]() $m \gg 0$,
$m \gg 0$, ![]() $V_m = V_{m+1} = \cdots =: V$ is the graph of the
$V_m = V_{m+1} = \cdots =: V$ is the graph of the ![]() $\mathcal {M}$-equivalence relation (with its reduced scheme structure). Denote by
$\mathcal {M}$-equivalence relation (with its reduced scheme structure). Denote by ![]() $V(x)$ the
$V(x)$ the ![]() $\mathcal {M}$-equivalence class of
$\mathcal {M}$-equivalence class of ![]() $x \in X$, which is the fiber of
$x \in X$, which is the fiber of ![]() $V/X_2$ over the point
$V/X_2$ over the point ![]() $x$. Note that
$x$. Note that ![]() $P$ and
$P$ and ![]() $Q$ are smooth.
$Q$ are smooth.
Let ![]() $\eta$ be the generic point of
$\eta$ be the generic point of ![]() $X_2$ and
$X_2$ and ![]() $K$ the algebraic closure of
$K$ the algebraic closure of ![]() $k(\eta )$. For a scheme
$k(\eta )$. For a scheme ![]() $S$ over
$S$ over ![]() $X_2$ or a morphism
$X_2$ or a morphism ![]() $f$ of
$f$ of ![]() $X_2$-schemes, we will denote by
$X_2$-schemes, we will denote by ![]() $S_K$ or
$S_K$ or ![]() $f_K$ the base change of
$f_K$ the base change of ![]() $S$ by the natural morphism
$S$ by the natural morphism ![]() $\operatorname {Spec} K \to X_2$. Note that this morphism
$\operatorname {Spec} K \to X_2$. Note that this morphism ![]() $\operatorname {Spec} K \to X_2$ is flat and that taking scheme theoretic image commutes with flat base changes.
$\operatorname {Spec} K \to X_2$ is flat and that taking scheme theoretic image commutes with flat base changes.
By induction, we will prove ![]() $(V_i)_K$ are reduced;
$(V_i)_K$ are reduced; ![]() $(V_0)_K$ is reduced since is isomorphic to
$(V_0)_K$ is reduced since is isomorphic to ![]() $\operatorname {Spec} K$. Assume that
$\operatorname {Spec} K$. Assume that ![]() $(V_i)_K$ is reduced. Since
$(V_i)_K$ is reduced. Since ![]() $Q$ is a smooth morphism,
$Q$ is a smooth morphism, ![]() $(Q^{-1}(V_i))_K$ is also reduced. Since taking scheme theoretic image commutes with flat base changes,
$(Q^{-1}(V_i))_K$ is also reduced. Since taking scheme theoretic image commutes with flat base changes, ![]() $(P(Q^{-1}(V_i)))_K$ is isomorphic to
$(P(Q^{-1}(V_i)))_K$ is isomorphic to ![]() $P_K((Q^{-1}(V_i))_K)$, which is reduced. Similarly
$P_K((Q^{-1}(V_i))_K)$, which is reduced. Similarly ![]() $(P^{-1}(P(Q^{-1}(V_i))))_K$ and
$(P^{-1}(P(Q^{-1}(V_i))))_K$ and ![]() $(Q(P^{-1}(P(Q^{-1}(V_i)))))_K$ are reduced. Thus,
$(Q(P^{-1}(P(Q^{-1}(V_i)))))_K$ are reduced. Thus, ![]() $(V_{i+1})_K$ is reduced.
$(V_{i+1})_K$ is reduced.
Step 4 Set ![]() $V^0 := \{(x,y) \in V \mid \text{$p_2^{-1}(y)$ is reduced} \}$. In this step, we show that:
$V^0 := \{(x,y) \in V \mid \text{$p_2^{-1}(y)$ is reduced} \}$. In this step, we show that:
–
 $X_i^0:= p_i(V^0)$ is open in
$X_i^0:= p_i(V^0)$ is open in  $X_i$ and
$X_i$ and  $p_i^{-1}(X_i^0) = V^0$; moreover,
$p_i^{-1}(X_i^0) = V^0$; moreover,  $V^0 \to X_i^0$ is smooth;
$V^0 \to X_i^0$ is smooth;–
 $Y^0 := f(X_i^0)$ is independent of
$Y^0 := f(X_i^0)$ is independent of  $i=1$,
$i=1$,  $2$; moreover,
$2$; moreover,  $Y^0$ is open in
$Y^0$ is open in  $Y$ and
$Y$ and  $X_i^0 = f^{-1}(Y^0)$.
$X_i^0 = f^{-1}(Y^0)$.
By Theorem 4.4, ![]() $p_2$ is smooth at
$p_2$ is smooth at ![]() $(x,y) \in V$ if and only if
$(x,y) \in V$ if and only if ![]() $p_2^{-1}(y)$ is generically reduced. In particular,
$p_2^{-1}(y)$ is generically reduced. In particular, ![]() $p_2^{-1}(y)$ is generically reduced if and only if
$p_2^{-1}(y)$ is generically reduced if and only if ![]() $p_2^{-1}(y)$ is reduced.
$p_2^{-1}(y)$ is reduced.
Note that ![]() $V$ is the graph of an equivalence relation. From this symmetry, it follows that
$V$ is the graph of an equivalence relation. From this symmetry, it follows that ![]() $p_2^{-1}(y) = p_1^{-1}(x)$ for
$p_2^{-1}(y) = p_1^{-1}(x)$ for ![]() $(x,y) \in V$. In particular,
$(x,y) \in V$. In particular, ![]() $p_2^{-1}(y)$ is reduced if and only if
$p_2^{-1}(y)$ is reduced if and only if ![]() $p_1^{-1}(x)$ is reduced. Thus, we have
$p_1^{-1}(x)$ is reduced. Thus, we have
Then ![]() $X_i^0 = p_i(V^0)$ is open in
$X_i^0 = p_i(V^0)$ is open in ![]() $X_i$ and
$X_i$ and ![]() $p_i^{-1}(X_i^0) = V^0$. Note that the subset
$p_i^{-1}(X_i^0) = V^0$. Note that the subset ![]() $Y^0 := f(X_i^0)$ is independent of
$Y^0 := f(X_i^0)$ is independent of ![]() $i=1$,
$i=1$, ![]() $2$ because of the symmetry. Moreover,
$2$ because of the symmetry. Moreover, ![]() $Y^0$ is open in
$Y^0$ is open in ![]() $Y$ and
$Y$ and ![]() $X_i^0 = f^{-1}(Y^0)$ since
$X_i^0 = f^{-1}(Y^0)$ since ![]() $X_i \setminus X_i^0$ is a closed subset, which is a union of
$X_i \setminus X_i^0$ is a closed subset, which is a union of ![]() $\mathcal {M}$-equivalent classes.
$\mathcal {M}$-equivalent classes.
Step 5 Now we prove some fiber of ![]() $X^0_2 \to Y^0$ is generically reduced.
$X^0_2 \to Y^0$ is generically reduced.
Since ![]() $V^0/X_2^0$ is a smooth projective family of subschemes in
$V^0/X_2^0$ is a smooth projective family of subschemes in ![]() $X_1$, we have a morphism
$X_1$, we have a morphism ![]() $X_2^0 \to \operatorname {Hilb}(X_1)$. Then this map factors
$X_2^0 \to \operatorname {Hilb}(X_1)$. Then this map factors ![]() $Y^0$ by the rigidity lemma [Reference DebarreDeb01, Lemma 1.15].
$Y^0$ by the rigidity lemma [Reference DebarreDeb01, Lemma 1.15].
Consider the composite ![]() $\gamma \colon p_2^* T_{X_2^0}|_{V^0} \to T_{X _1^0 \times X_2^0}|_{V^0} \to N_{V^0/X_1^0 \times X_2^0}$ of natural homomorphisms. Then the restriction of
$\gamma \colon p_2^* T_{X_2^0}|_{V^0} \to T_{X _1^0 \times X_2^0}|_{V^0} \to N_{V^0/X_1^0 \times X_2^0}$ of natural homomorphisms. Then the restriction of ![]() $\gamma$ to
$\gamma$ to ![]() $p_1^{-1}(x_1)$ gives the surjection
$p_1^{-1}(x_1)$ gives the surjection
Thus, ![]() $\gamma$ is surjective. On the other hand, if we restrict
$\gamma$ is surjective. On the other hand, if we restrict ![]() $\gamma$ to
$\gamma$ to ![]() $p_2^{-1}(x_2)$, we have a surjection
$p_2^{-1}(x_2)$, we have a surjection
between trivial vector bundles. Hence, by taking global sections, we have a surjection
of vector spaces and, hence, the map ![]() $X_2^0 \to \operatorname {Hilb}(X_1)$ is a smooth morphism. Recall that we have the factorization
$X_2^0 \to \operatorname {Hilb}(X_1)$ is a smooth morphism. Recall that we have the factorization ![]() $X_2^0 \to Y^0 \to \operatorname {Hilb}(X_1)$ with a quasi-finite morphism
$X_2^0 \to Y^0 \to \operatorname {Hilb}(X_1)$ with a quasi-finite morphism ![]() $Y^0 \to \operatorname {Hilb}(X_1)$. Let
$Y^0 \to \operatorname {Hilb}(X_1)$. Let ![]() $U \subset Y^0$ be a non-empty open subset such that
$U \subset Y^0$ be a non-empty open subset such that ![]() $f^{-1}(U) \to U$ is flat. Then the morphism
$f^{-1}(U) \to U$ is flat. Then the morphism ![]() $U \to \operatorname {Hilb}(X_1)$ is étale. This implies that
$U \to \operatorname {Hilb}(X_1)$ is étale. This implies that ![]() $f^{-1} (U)\to U$ is smooth. In particular, some fiber of
$f^{-1} (U)\to U$ is smooth. In particular, some fiber of ![]() $X^0_2 \to Y^0$ is generically reduced. This completes the proof.
$X^0_2 \to Y^0$ is generically reduced. This completes the proof.
Proposition 4.6 Let ![]() $\mathcal {M}$ be a family as in the diagram (4.1) and
$\mathcal {M}$ be a family as in the diagram (4.1) and ![]() $[C] \in \mathcal {M}$ be a curve parametrized by
$[C] \in \mathcal {M}$ be a curve parametrized by ![]() $\mathcal {M}$. Assume that
$\mathcal {M}$. Assume that ![]() $q$ is smooth.
$q$ is smooth.
Then ![]() $R := \mathbb {R}_{\geq 0} [C]$ is an extremal ray of
$R := \mathbb {R}_{\geq 0} [C]$ is an extremal ray of ![]() $X$ and there exists a contraction
$X$ and there exists a contraction ![]() $f \colon X \to Y$ of
$f \colon X \to Y$ of ![]() $R$ satisfying:
$R$ satisfying:
(1)
 $f$ is smooth;
$f$ is smooth;(2) any fiber
 $F$ of
$F$ of  $f$ is an SRC Fano variety with nef tangent bundle;
$f$ is an SRC Fano variety with nef tangent bundle;(3)
 $T_Y$ is again nef.
$T_Y$ is again nef.
Proof. Let ![]() $\mathcal {U} \xrightarrow {q'} X' \xrightarrow {\alpha } X$ be the Stein factorization of
$\mathcal {U} \xrightarrow {q'} X' \xrightarrow {\alpha } X$ be the Stein factorization of ![]() $q$. Since
$q$. Since ![]() $q$ is smooth, so is
$q$ is smooth, so is ![]() $\alpha$ (see, for instance, [Reference GrothendieckGro63, 7.8.10 (i)]). Then we see that
$\alpha$ (see, for instance, [Reference GrothendieckGro63, 7.8.10 (i)]). Then we see that ![]() $q'$ is also smooth (with irreducible fibers).
$q'$ is also smooth (with irreducible fibers).
First we reduce to the case that the covering ![]() $\alpha$ is Galois. There exists a finite étale Galois cover
$\alpha$ is Galois. There exists a finite étale Galois cover ![]() $X'' \to X'$ such that the composite
$X'' \to X'$ such that the composite ![]() $X'' \to X' \to X$ is also a finite Galois étale cover (see, e.g., [Reference SzamuelySza09, Proposition 5.3.9]). Set
$X'' \to X' \to X$ is also a finite Galois étale cover (see, e.g., [Reference SzamuelySza09, Proposition 5.3.9]). Set ![]() $\mathcal {U}'' := \mathcal {U} \times _{X'} X''$ and
$\mathcal {U}'' := \mathcal {U} \times _{X'} X''$ and ![]() $\mathcal {U}'' \to \mathcal {M}'' \to \mathcal {M}$ be the Stein factorization of
$\mathcal {U}'' \to \mathcal {M}'' \to \mathcal {M}$ be the Stein factorization of ![]() $\mathcal {U}'' \to \mathcal {M}$. Then the morphism
$\mathcal {U}'' \to \mathcal {M}$. Then the morphism ![]() $\mathcal {U}'' \to \mathcal {M}''$ is a smooth
$\mathcal {U}'' \to \mathcal {M}''$ is a smooth ![]() $\mathbb {P}^1$-fibration and we have the following diagram.
$\mathbb {P}^1$-fibration and we have the following diagram.

Note that this diagram defines the same ray ![]() $R$ and the
$R$ and the ![]() $\mathcal {M}''$-equivalent relation is the
$\mathcal {M}''$-equivalent relation is the ![]() $\mathcal {M}$-equivalent relation. Moreover the Stein factorization of
$\mathcal {M}$-equivalent relation. Moreover the Stein factorization of ![]() $q''$ gives the Galois covering
$q''$ gives the Galois covering ![]() $X'' \to X$.
$X'' \to X$.
Therefore, we may assume that the map ![]() $\alpha$ is a finite Galois étale cover with Galois group
$\alpha$ is a finite Galois étale cover with Galois group ![]() $G := \{g_1, \ldots, g_m\}$. By composing
$G := \{g_1, \ldots, g_m\}$. By composing ![]() $g_i$ with
$g_i$ with ![]() $q'$, we have the following diagrams.
$q'$, we have the following diagrams.

By Proposition 4.3, there exist the contractions of extremal rays ![]() $R_i := (g_i)_*R$.
$R_i := (g_i)_*R$.
Let ![]() $f_1 \colon X' \to Y_1$ be the contraction of
$f_1 \colon X' \to Y_1$ be the contraction of ![]() $R_1$. Then
$R_1$. Then ![]() $f_1$ is a smooth morphism by Proposition 4.5. Thus, the following diagram
$f_1$ is a smooth morphism by Proposition 4.5. Thus, the following diagram

satisfies the assumption of Propositions 4.3 and 4.5 if ![]() $p_i$-fibers are not contracted to a point in
$p_i$-fibers are not contracted to a point in ![]() $Y_1$.
$Y_1$.
If all rays ![]() $R_i$ are contracted by
$R_i$ are contracted by ![]() $g \colon X' \to Y_1$, then we have a smooth contraction
$g \colon X' \to Y_1$, then we have a smooth contraction ![]() $g \colon X' \to Y_1$ whose fibers are
$g \colon X' \to Y_1$ whose fibers are ![]() $\mathcal {M}_1$-equivalent classes, and
$\mathcal {M}_1$-equivalent classes, and ![]() $g$ contracts all rays
$g$ contracts all rays ![]() $R_i$. Otherwise, for some
$R_i$. Otherwise, for some ![]() $i$, the ray
$i$, the ray ![]() $R_i$ is not contracted by
$R_i$ is not contracted by ![]() $X \to Y_1$ and, hence,
$X \to Y_1$ and, hence, ![]() $p_i$-fibers are not contracted to a point in
$p_i$-fibers are not contracted to a point in ![]() $Y_1$. Then, by applying the same argument above, we have a smooth contraction
$Y_1$. Then, by applying the same argument above, we have a smooth contraction ![]() $Y_1 \to Y_2$ whose fibers are
$Y_1 \to Y_2$ whose fibers are ![]() $\mathcal {M}_i$-equivalent classes.
$\mathcal {M}_i$-equivalent classes.
Thus, by repeating this procedure, we have a sequence of morphism ![]() $X' \to Y_1 \to \cdots \to Y_l$ such that each morphism is a smooth contraction whose fibers are
$X' \to Y_1 \to \cdots \to Y_l$ such that each morphism is a smooth contraction whose fibers are ![]() $\mathcal {M}_j$-equivalent classes for some
$\mathcal {M}_j$-equivalent classes for some ![]() $j$ and that all rays
$j$ and that all rays ![]() $R_i$ are contracted by
$R_i$ are contracted by ![]() $g \colon X' \to Y_l$.
$g \colon X' \to Y_l$.
Since each fiber of ![]() $g$ is chain connected by curves in the families
$g$ is chain connected by curves in the families ![]() $\mathcal {M}_i$, each fiber of
$\mathcal {M}_i$, each fiber of ![]() $g$ is an
$g$ is an ![]() $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. Since the set of diagrams
$(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. Since the set of diagrams ![]() $\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ is
$\{ (\mathcal {M}_i \xleftarrow {p_i} \mathcal {U}_i \xrightarrow {q_i} X)\}_{i=1,\ldots,m}$ is ![]() $G$-invariant, the
$G$-invariant, the ![]() $g_i$-image (
$g_i$-image (![]() $g_i \in G$) of an
$g_i \in G$) of an ![]() $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class is again an
$(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class is again an ![]() $(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. This implies that there exists a
$(\mathcal {M}_1, \ldots, \mathcal {M}_m)$-equivalence class. This implies that there exists a ![]() $G$-action on
$G$-action on ![]() $Y_l$ such that
$Y_l$ such that ![]() $g$ is
$g$ is ![]() $G$-equivariant. By Lemma 4.1, there exists a contraction
$G$-equivariant. By Lemma 4.1, there exists a contraction ![]() $f \colon X \to Y$ such that the following diagram commutes.
$f \colon X \to Y$ such that the following diagram commutes.

Since ![]() $g$ is smooth, any fiber of
$g$ is smooth, any fiber of ![]() $f$ is irreducible and the image of a
$f$ is irreducible and the image of a ![]() $g$-fiber (Lemma 4.1). Thus, each
$g$-fiber (Lemma 4.1). Thus, each ![]() $f$-fiber is an
$f$-fiber is an ![]() $\mathcal {M}$-equivalent class and
$\mathcal {M}$-equivalent class and ![]() $f$ is equidimensional with irreducible fibers. Hence,
$f$ is equidimensional with irreducible fibers. Hence, ![]() $f$ satisfies the assumption of Proposition 4.5 and the assertions follow.
$f$ satisfies the assumption of Proposition 4.5 and the assertions follow.
Remark 4.7 Assume ![]() $X$ is RCC, then
$X$ is RCC, then ![]() $X$ is algebraically simply connected. Thus, the map
$X$ is algebraically simply connected. Thus, the map ![]() $\mathcal {U} \to X$ has connected fibers. In this case, by Proposition 4.3, we have
$\mathcal {U} \to X$ has connected fibers. In this case, by Proposition 4.3, we have ![]() $\rho (F) = 1$ for any fiber
$\rho (F) = 1$ for any fiber ![]() $F$ of the extremal contraction
$F$ of the extremal contraction
Proof of Theorem 1.5 Take a rational curve ![]() $C$ on
$C$ on ![]() $X$ such that
$X$ such that ![]() $R=\mathbb {R}_{\geq 0}[C]$ and the anti-canonical degree of
$R=\mathbb {R}_{\geq 0}[C]$ and the anti-canonical degree of ![]() $C$ is minimal among rational curves in the ray
$C$ is minimal among rational curves in the ray ![]() $R$. Let
$R$. Let ![]() $\mathcal {M}$ be the unsplit family of rational curves containing
$\mathcal {M}$ be the unsplit family of rational curves containing ![]() $[C]$:
$[C]$:

Then ![]() $q$ is smooth and the assertion follows from Proposition 4.6.
$q$ is smooth and the assertion follows from Proposition 4.6.
5. Rational chain connectedness and positivity of  $-K_X$
$-K_X$
In this section, we prove Theorem 1.6. The proof proceeds as [Reference WatanabeWat21, Proof of Theorem 4.16]. Here we divide the proof into several steps.
Throughout this section:
–
 $X$ denotes a smooth projective variety with nef tangent bundle and
$X$ denotes a smooth projective variety with nef tangent bundle and  $f \colon X \to Y$ is a smooth contraction with RCC fibers.
$f \colon X \to Y$ is a smooth contraction with RCC fibers.
Note that by Theorem 1.3 all fibers are SRC.
Lemma 5.1 (Correspondence of extremal rays)
Suppose that ![]() $R_Y$ is an extremal ray of
$R_Y$ is an extremal ray of ![]() $\,Y$. Then there exists an extremal ray
$\,Y$. Then there exists an extremal ray ![]() $R_X$ of
$R_X$ of ![]() $X$ such that
$X$ such that ![]() $f_*R _X =R_Y$.
$f_*R _X =R_Y$.
On the other hand, if ![]() $R_X$ is an extremal ray of
$R_X$ is an extremal ray of ![]() $X$, then
$X$, then ![]() $f_* R_X$ is an extremal ray unless
$f_* R_X$ is an extremal ray unless ![]() $f_* R_X = 0$.
$f_* R_X = 0$.
Proof. Let ![]() $C_Y$ be a rational curve such that the class belongs to
$C_Y$ be a rational curve such that the class belongs to ![]() $R_Y$ and
$R_Y$ and ![]() $-K_Y \cdot C_Y$ is minimum. Since any fiber of
$-K_Y \cdot C_Y$ is minimum. Since any fiber of ![]() $f$ is RCC, it is SRC by Theorem 1.3. Thus, by [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03], there exists a rational curve
$f$ is RCC, it is SRC by Theorem 1.3. Thus, by [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03], there exists a rational curve ![]() $C_X$ on
$C_X$ on ![]() $X$ such that
$X$ such that ![]() $f|_{C_X} \colon C_X \to C_Y$ is birational. Take such a rational curve
$f|_{C_X} \colon C_X \to C_Y$ is birational. Take such a rational curve ![]() $C_X$ with minimum anti-canonical degree
$C_X$ with minimum anti-canonical degree ![]() $-K_X \cdot C_X$ (note that, since
$-K_X \cdot C_X$ (note that, since ![]() $T_X$ is nef, the
$T_X$ is nef, the ![]() $(-K_X)$-degree of any rational curve is at least
$(-K_X)$-degree of any rational curve is at least ![]() $2$).
$2$).
Then, by the minimality of ![]() $-K_X$-degree, the family of rational curves of
$-K_X$-degree, the family of rational curves of ![]() $C_X$ is unsplit. Thus, by Proposition 4.6,
$C_X$ is unsplit. Thus, by Proposition 4.6, ![]() $\mathbb {R}_{\geq 0} [C_X]$ defines an extremal ray of
$\mathbb {R}_{\geq 0} [C_X]$ defines an extremal ray of ![]() $X$.
$X$.
Conversely, assume that ![]() $R_X$ is an extremal ray of
$R_X$ is an extremal ray of ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be a family of minimal rational curves in
$\mathcal {M}$ be a family of minimal rational curves in ![]() $R_X$ and let
$R_X$ and let

be the diagram of this family of rational curves. Then ![]() $f \circ q$ gives a diagram satisfying the assumption of Proposition 4.6 and, hence,
$f \circ q$ gives a diagram satisfying the assumption of Proposition 4.6 and, hence, ![]() $f_*R_X$ is an extremal ray.
$f_*R_X$ is an extremal ray.
Proposition 5.2 (Relative Picard numbers)
Let ![]() $Y \to Z$ be another contraction. Then
$Y \to Z$ be another contraction. Then ![]() $\rho (X/Y) =\rho (X/Z) - \rho (Y/Z)$ and we have the following exact sequence:
$\rho (X/Y) =\rho (X/Z) - \rho (Y/Z)$ and we have the following exact sequence:
Proof. Note that any ![]() $f$-fiber
$f$-fiber ![]() $F$ is SRC and, in particular, any numerically trivial line bundle on
$F$ is SRC and, in particular, any numerically trivial line bundle on ![]() $F$ is trivial (Corollary 2.4).
$F$ is trivial (Corollary 2.4).
Thus, the sequence
is exact and the assertions follow.
Theorem 5.3 (Relative Kleiman–Mori cone)
Fix an integer ![]() $m$, then the following are equivalent:
$m$, then the following are equivalent:
(1)
 $\rho (X/Y) =m$;
$\rho (X/Y) =m$;(2) there exists a sequence of smooth contractions of
 $K$-negative extremal rays
$K$-negative extremal rays
 \[ X=X_0 \to X_1 \to X_2 \to \cdots \to X_{m-1} \to X_{m} = Y; \]
\[ X=X_0 \to X_1 \to X_2 \to \cdots \to X_{m-1} \to X_{m} = Y; \]
(3)
 $\operatorname {NE} (X/Y)$ is a closed simplicial cone of dimension
$\operatorname {NE} (X/Y)$ is a closed simplicial cone of dimension  $m$, and it is generated by
$m$, and it is generated by  $K_X$-negative extremal rays.
$K_X$-negative extremal rays.
In particular, any fiber ![]() $F$ is a smooth Fano variety.
$F$ is a smooth Fano variety.
Proof. The proof proceeds by induction on ![]() $m$. If
$m$. If ![]() $m =1$, then the equivalence of the three conditions follows from Theorem 1.5.
$m =1$, then the equivalence of the three conditions follows from Theorem 1.5.
Assume ![]() $m \geq 2$. Note that (3)
$m \geq 2$. Note that (3) ![]() $\implies$ (1) is trivial. Also note that Proposition 5.2 implies (2)
$\implies$ (1) is trivial. Also note that Proposition 5.2 implies (2) ![]() $\implies$ (1).
$\implies$ (1).
Now, we prove (1) ![]() $\implies$ (2). Since
$\implies$ (2). Since ![]() $K_X$ is not
$K_X$ is not ![]() $f$-nef, there exists a
$f$-nef, there exists a ![]() $K_X$-negative extremal ray
$K_X$-negative extremal ray ![]() $R \subset \overline {\operatorname {NE}} (X/Y)$. By Theorem 1.5, there exists a smooth contraction
$R \subset \overline {\operatorname {NE}} (X/Y)$. By Theorem 1.5, there exists a smooth contraction ![]() $f_1 \colon X \to X_1$ of
$f_1 \colon X \to X_1$ of ![]() $R$, and
$R$, and ![]() $f$ factors through
$f$ factors through ![]() $X_1$:
$X_1$:
Since ![]() $f_1$ is smooth and any fiber of
$f_1$ is smooth and any fiber of ![]() $f$ is RCC, the morphism
$f$ is RCC, the morphism ![]() $X_1 \to Y$ is also smooth and fibers are RCC. Since
$X_1 \to Y$ is also smooth and fibers are RCC. Since ![]() $\rho (X_1/Y)< m$, the contraction
$\rho (X_1/Y)< m$, the contraction ![]() $X_1 \to Y$ satisfies the three conditions. Hence, condition (2) holds for
$X_1 \to Y$ satisfies the three conditions. Hence, condition (2) holds for ![]() $f \colon X \to Y$.
$f \colon X \to Y$.
Finally, we prove (2) ![]() $\implies$ (3). Since
$\implies$ (3). Since ![]() $\rho (X/X_{m-1}) < m$ by Proposition 5.2, the contraction
$\rho (X/X_{m-1}) < m$ by Proposition 5.2, the contraction ![]() $g \colon X \to X_{m-1}$ satisfies the three conditions. In particular,
$g \colon X \to X_{m-1}$ satisfies the three conditions. In particular, ![]() $\operatorname {NE}(X/{X_{m-1}})$ is a simplicial
$\operatorname {NE}(X/{X_{m-1}})$ is a simplicial ![]() $K_X$-negative face of dimension
$K_X$-negative face of dimension ![]() $m-1$. Denote by
$m-1$. Denote by ![]() $R_1 =\mathbb {R}_{\geq 0} [C_1]$, …,
$R_1 =\mathbb {R}_{\geq 0} [C_1]$, …, ![]() $R_{m-1}=\mathbb {R}_{\geq 0} [C_{m-1}]$ the extremal rays of
$R_{m-1}=\mathbb {R}_{\geq 0} [C_{m-1}]$ the extremal rays of ![]() $\operatorname {NE}(X/{X_{m-1}})$, which are spanned by curves
$\operatorname {NE}(X/{X_{m-1}})$, which are spanned by curves ![]() $C_i$. Note also that
$C_i$. Note also that ![]() $X_{m-1} \to Y$ is a contraction of an extremal ray
$X_{m-1} \to Y$ is a contraction of an extremal ray ![]() $R_{X_{m-1}}$.
$R_{X_{m-1}}$.
Then, by Lemma 5.1, there exists an extremal ray ![]() $R$ of
$R$ of ![]() $X$ such that
$X$ such that ![]() $g_* R = R_{X_{m-1}}$. Let
$g_* R = R_{X_{m-1}}$. Let ![]() $h \colon X \to Z$ be the contraction of
$h \colon X \to Z$ be the contraction of ![]() $R$, then we have the following commutative diagram.
$R$, then we have the following commutative diagram.

Note that, by the inductive hypothesis, each morphism ![]() $g$,
$g$, ![]() $h$,
$h$, ![]() $u$, and
$u$, and ![]() $v$ satisfies the three conditions. Since
$v$ satisfies the three conditions. Since ![]() $N_1(X/X_{m-1}) \to N_1(Z/Y)$ is a surjective homomorphism between the same dimensional vector spaces, it is an isomorphism.
$N_1(X/X_{m-1}) \to N_1(Z/Y)$ is a surjective homomorphism between the same dimensional vector spaces, it is an isomorphism.
By Lemma 5.1, the map ![]() $N_1(X/X_{m-1}) \to N_1(Z/Y)$ sends each extremal ray to an extremal ray. Thus,
$N_1(X/X_{m-1}) \to N_1(Z/Y)$ sends each extremal ray to an extremal ray. Thus, ![]() $\overline {\operatorname {NE}}(X/X_{m-1}) \simeq \overline {\operatorname {NE}}(Z/Y)$ since these two cones are simplicial. In particular,
$\overline {\operatorname {NE}}(X/X_{m-1}) \simeq \overline {\operatorname {NE}}(Z/Y)$ since these two cones are simplicial. In particular, ![]() $\overline {\operatorname {NE}}(Z/Y)$ is spanned by
$\overline {\operatorname {NE}}(Z/Y)$ is spanned by ![]() $h_*(C_i)$ (
$h_*(C_i)$ (![]() $i=1$, …,
$i=1$, …, ![]() $m-1$).
$m-1$).
Let ![]() $C$ be an irreducible curve on
$C$ be an irreducible curve on ![]() $X$ such that
$X$ such that ![]() $f(C)$ is a point. Then
$f(C)$ is a point. Then ![]() $h_*(C) \in \operatorname {NE}(Z/Y)$. Thus, we may write
$h_*(C) \in \operatorname {NE}(Z/Y)$. Thus, we may write
 \[ h_*(C) = \sum_{i=1}^{m-1} a_i h_*(C_i) \]
\[ h_*(C) = \sum_{i=1}^{m-1} a_i h_*(C_i) \]
with non-negative real numbers ![]() $a_i$. Thus,
$a_i$. Thus, ![]() $C - \sum _{i=1}^{m-1} a_i C_i \in \operatorname {Ker}(h_*) = N_1(X/Z)$. Since
$C - \sum _{i=1}^{m-1} a_i C_i \in \operatorname {Ker}(h_*) = N_1(X/Z)$. Since ![]() $g^*H \cdot (C - \sum _{i=1}^{m-1} a_i C_i) \geq 0$ for any ample divisor
$g^*H \cdot (C - \sum _{i=1}^{m-1} a_i C_i) \geq 0$ for any ample divisor ![]() $H$ on
$H$ on ![]() $X_{m-1}$, we see that
$X_{m-1}$, we see that
 \[ C - \sum_{i=1}^{m-1} a_i C_i \in R. \]
\[ C - \sum_{i=1}^{m-1} a_i C_i \in R. \]
This proves ![]() $\overline {\operatorname {NE}}(X/Y)$ is spanned by
$\overline {\operatorname {NE}}(X/Y)$ is spanned by ![]() $R,R_1,\ldots,R_{m-1}$, and hence it is simplicial (since
$R,R_1,\ldots,R_{m-1}$, and hence it is simplicial (since ![]() $\rho (X/Y) =m$).
$\rho (X/Y) =m$).
Remark 5.4 If ![]() $X$ is RCC or, equivalently, a Fano variety, then each
$X$ is RCC or, equivalently, a Fano variety, then each ![]() $X_i$ is also a Fano variety. Thus, by Remark 4.7, the fibers of
$X_i$ is also a Fano variety. Thus, by Remark 4.7, the fibers of ![]() $X_i \to X_{i+1}$ have Picard number one. Then, by arguing as above, we can show that each fiber
$X_i \to X_{i+1}$ have Picard number one. Then, by arguing as above, we can show that each fiber ![]() $F$ of the contraction
$F$ of the contraction ![]() $X \to Y$ is a Fano variety with
$X \to Y$ is a Fano variety with ![]() $\rho (F) = m$. Moreover,
$\rho (F) = m$. Moreover, ![]() $N_1(F)$ and
$N_1(F)$ and ![]() $\operatorname {NE}(F)$ are identified with
$\operatorname {NE}(F)$ are identified with ![]() $N_1(X/Y)$ and
$N_1(X/Y)$ and ![]() $\operatorname {NE}(X/Y)$, respectively, via the inclusion.
$\operatorname {NE}(X/Y)$, respectively, via the inclusion.
6. Decomposition of varieties with nef tangent bundles
Proof of Theorem 1.8 Here we will prove Theorem 1.8. If ![]() $K_X$ is nef, then
$K_X$ is nef, then ![]() $T_X$ is numerically flat and
$T_X$ is numerically flat and ![]() $\varphi =\operatorname {id} \colon X \to X$ gives the desired contraction.
$\varphi =\operatorname {id} \colon X \to X$ gives the desired contraction.
Assume that ![]() $K_X$ is not nef. By Mori's cone theorem, we can find an extremal ray
$K_X$ is not nef. By Mori's cone theorem, we can find an extremal ray ![]() $R \subset \overline {\operatorname {NE}}(X)$ of
$R \subset \overline {\operatorname {NE}}(X)$ of ![]() $X$. Then, by Theorem 1.5, there exists a smooth contraction
$X$. Then, by Theorem 1.5, there exists a smooth contraction ![]() $f \colon X \to Y$ of
$f \colon X \to Y$ of ![]() $R$ and the tangent bundle of
$R$ and the tangent bundle of ![]() $Y$ is again nef. By induction on the dimension,
$Y$ is again nef. By induction on the dimension, ![]() $Y$ admits a smooth contraction
$Y$ admits a smooth contraction ![]() $\varphi ' \colon Y \to M$ satisfying the conditions in Theorem 1.8. Set
$\varphi ' \colon Y \to M$ satisfying the conditions in Theorem 1.8. Set ![]() $\varphi := \varphi ' \circ f$.
$\varphi := \varphi ' \circ f$.
Let ![]() $F$ be a fiber of
$F$ be a fiber of ![]() $\varphi$. Then
$\varphi$. Then ![]() $T_F$ is nef. Moreover, since any fiber of
$T_F$ is nef. Moreover, since any fiber of ![]() $f$ is SRC and any fiber of
$f$ is SRC and any fiber of ![]() $\varphi '$ is RCC, it follows that
$\varphi '$ is RCC, it follows that ![]() $F$ is RCC [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03]. Hence,
$F$ is RCC [Reference Graber, Harris and StarrGHS03, Reference de Jong and StarrdJS03]. Hence, ![]() $F$ is a smooth Fano variety by Theorem 1.6.
$F$ is a smooth Fano variety by Theorem 1.6.
Corollary 6.1 (Contraction of extremal faces)
Let ![]() $X$ be a smooth projective variety with nef tangent bundle and
$X$ be a smooth projective variety with nef tangent bundle and ![]() $\varphi \colon X \to M$ be the decomposition morphism as in Theorem 1.8. Then
$\varphi \colon X \to M$ be the decomposition morphism as in Theorem 1.8. Then ![]() $\operatorname {NE}(X/M)$ is simplicial. Any set of
$\operatorname {NE}(X/M)$ is simplicial. Any set of ![]() $K_X$-negative extremal rays spans an extremal face.
$K_X$-negative extremal rays spans an extremal face.
Moreover, for any ![]() $K_X$-negative extremal face
$K_X$-negative extremal face ![]() $F$, there exists the contraction of
$F$, there exists the contraction of ![]() $F$ and it is a smooth morphism satisfies the three equivalent conditions in Theorem 5.3.
$F$ and it is a smooth morphism satisfies the three equivalent conditions in Theorem 5.3.
7.  $F$-liftable varieties with nef tangent bundles
$F$-liftable varieties with nef tangent bundles
Here we apply our results to prove Theorem 1.12
7.1 Preliminaries on  $F$-liftability
$F$-liftability
Definition 7.1 ( $F$-liftable varieties)
$F$-liftable varieties)
Let ![]() $X$ be a projective variety over
$X$ be a projective variety over ![]() $k$.
$k$.
(1) A lifting of
 $X$ (modulo
$X$ (modulo  $p^2$) is a flat scheme
$p^2$) is a flat scheme  $\widetilde {X}$ over the ring
$\widetilde {X}$ over the ring  $W_2(k)$ of Witt vectors of length two with
$W_2(k)$ of Witt vectors of length two with  $\widetilde {X}\times _{{\operatorname {Spec}} W_2(k)} \operatorname {Spec} (k) \cong X$.
$\widetilde {X}\times _{{\operatorname {Spec}} W_2(k)} \operatorname {Spec} (k) \cong X$.(2) For such a lifting
 $\widetilde {X}$ of
$\widetilde {X}$ of  $X$, a lifting of Frobenius on
$X$, a lifting of Frobenius on  $X$ to
$X$ to  $\widetilde {X}$ is a morphism
$\widetilde {X}$ is a morphism  $\widetilde {F_X} \colon \widetilde {X} \to \widetilde {X}$ such that the restriction
$\widetilde {F_X} \colon \widetilde {X} \to \widetilde {X}$ such that the restriction  $\widetilde {F_X}|_X$ coincides with the Frobenius morphism
$\widetilde {F_X}|_X$ coincides with the Frobenius morphism  $F_X$; then the pair
$F_X$; then the pair  $(\widetilde {X}, \widetilde {F_X})$ is called a Frobenius lifting of
$(\widetilde {X}, \widetilde {F_X})$ is called a Frobenius lifting of  $X$. If there exists such a pair,
$X$. If there exists such a pair,  $X$ is said to be F-liftable.
$X$ is said to be F-liftable.
Proposition 7.2 ( $F$-liftable varieties)
$F$-liftable varieties)
For a smooth ![]() $F$-liftable projective variety
$F$-liftable projective variety ![]() $X$, the following hold.
$X$, the following hold.
(1) For any finite étale cover
 $Y \to X$,
$Y \to X$,  $Y$ is also F-liftable.
$Y$ is also F-liftable.(2) Let
 $f \colon X \to Y$ be a contraction and assume
$f \colon X \to Y$ be a contraction and assume  $R^1f_{\ast }\mathcal {O}_X=0$. Then
$R^1f_{\ast }\mathcal {O}_X=0$. Then  $Y$ and any fiber
$Y$ and any fiber  $F$ of
$F$ of  $f$ are also F-liftable.
$f$ are also F-liftable.
Proof. Part (1) follows from [Reference Achinger, Witaszek and ZdanowiczAWZ21, Lemma 3.3.5]. Part (2) follows from [Reference Achinger, Witaszek and ZdanowiczAWZ21, Theorem 3.3.6 (b)] and [Reference Achinger, Witaszek and ZdanowiczAWZ23, Corollary 5.3 (b)].
7.2 Proof of Theorem 1.12
Definition 7.3 ( $F$-liftable and nef tangent bundle)
$F$-liftable and nef tangent bundle)
Let ![]() $X$ be a smooth projective variety. For convenience, let us introduce the following condition:
$X$ be a smooth projective variety. For convenience, let us introduce the following condition:
(FLNT)
 $X$ is
$X$ is  $F$-liftable and the tangent bundle is nef.
$F$-liftable and the tangent bundle is nef.
Proposition 7.4 [Reference Achinger, Witaszek and ZdanowiczAWZ21, Proposition 6.3.2]
Let ![]() $X$ be a smooth Fano variety satisfying the condition (FLNT). If
$X$ be a smooth Fano variety satisfying the condition (FLNT). If ![]() $\rho _X=1$, then
$\rho _X=1$, then ![]() $X$ is isomorphic to a projective space.
$X$ is isomorphic to a projective space.
Proposition 7.5 ( $F$-liftable varieties with
$F$-liftable varieties with  $K_X \equiv 0$)
$K_X \equiv 0$)
Let ![]() $X$ be a smooth projective
$X$ be a smooth projective ![]() $F$-liftable variety. If the canonical divisor
$F$-liftable variety. If the canonical divisor ![]() $K_X$ is numerically trivial, then there exists a finite étale cover
$K_X$ is numerically trivial, then there exists a finite étale cover ![]() $f\colon Y \to X$ from an ordinary abelian variety
$f\colon Y \to X$ from an ordinary abelian variety ![]() $Y$.
$Y$.
Proof. See, for instance, [Reference Achinger, Witaszek and ZdanowiczAWZ21, Theorem 5.1.1].
Proposition 7.6 (FLNT Fano varieties)
Let ![]() $X$ be a smooth Fano variety satisfying the condition (FLNT). Then
$X$ be a smooth Fano variety satisfying the condition (FLNT). Then ![]() $X$ is isomorphic to a product of projective spaces.
$X$ is isomorphic to a product of projective spaces.
Proof. We proceed by induction on the Picard number ![]() $\rho _X$. By Proposition 7.4, our assertion holds for the case
$\rho _X$. By Proposition 7.4, our assertion holds for the case ![]() $\rho _X=1$. Assume that
$\rho _X=1$. Assume that ![]() $\rho _X \geq 2$. Then there exists a two-dimensional extremal face, which is spanned by two extremal rays
$\rho _X \geq 2$. Then there exists a two-dimensional extremal face, which is spanned by two extremal rays ![]() $R_1$ and
$R_1$ and ![]() $R_2$. We denote the contraction of the extremal ray
$R_2$. We denote the contraction of the extremal ray ![]() $R_i$ by
$R_i$ by ![]() $f_i\colon X \to X_i$ (
$f_i\colon X \to X_i$ (![]() $i=1$,
$i=1$, ![]() $2$), which is a smooth
$2$), which is a smooth ![]() $\mathbb {P}$-fibration by Theorem 1.5, Remark 4.7, and Proposition 7.4. By the induction hypothesis, each
$\mathbb {P}$-fibration by Theorem 1.5, Remark 4.7, and Proposition 7.4. By the induction hypothesis, each ![]() $X_i$ is a product of projective spaces and, hence, the Brauer group of
$X_i$ is a product of projective spaces and, hence, the Brauer group of ![]() $X_i$ vanishes; this implies that each
$X_i$ vanishes; this implies that each ![]() $f_i$ is given by a projectivization of a vector bundle. When
$f_i$ is given by a projectivization of a vector bundle. When ![]() $\rho _X=2$, applying [Reference SatoSat85, Theorem A]
$\rho _X=2$, applying [Reference SatoSat85, Theorem A] ![]() $X$ is isomorphic to a product of two projective spaces or
$X$ is isomorphic to a product of two projective spaces or ![]() $\mathbb {P}(T_{\mathbb {P}^n})$. However, the latter does not occur, because
$\mathbb {P}(T_{\mathbb {P}^n})$. However, the latter does not occur, because ![]() $\mathbb {P}(T_{\mathbb {P}^n})$ is not F-liftable by [Reference Achinger, Witaszek and ZdanowiczAWZ21, Lemma 6.4.3]. Thus, we may assume that
$\mathbb {P}(T_{\mathbb {P}^n})$ is not F-liftable by [Reference Achinger, Witaszek and ZdanowiczAWZ21, Lemma 6.4.3]. Thus, we may assume that ![]() $\rho _X \geq 3$. Let
$\rho _X \geq 3$. Let ![]() $\pi \colon X \to X_{1,2}$ be the contraction of the extremal face
$\pi \colon X \to X_{1,2}$ be the contraction of the extremal face ![]() $R_1+R_2$. By the rigidity lemma [Reference DebarreDeb01, Lemma 1.15], there is the following commutative diagram.
$R_1+R_2$. By the rigidity lemma [Reference DebarreDeb01, Lemma 1.15], there is the following commutative diagram.

Let us take a vector bundle ![]() $\mathcal {E}$ on
$\mathcal {E}$ on ![]() $X_1$ such that
$X_1$ such that ![]() $X \cong \mathbb {P}(\mathcal {E})$ and
$X \cong \mathbb {P}(\mathcal {E})$ and ![]() $f_1\colon X \to X_1$ is given by the natural projection
$f_1\colon X \to X_1$ is given by the natural projection ![]() $\mathbb {P}(\mathcal {E}) \to X_1$. For any point
$\mathbb {P}(\mathcal {E}) \to X_1$. For any point ![]() $p \in X_{1,2}$,
$p \in X_{1,2}$, ![]() $\pi ^{-1}(p)$ is a smooth Fano variety of Picard number two satisfying the condition (FLNT); by the induction hypothesis it is a product of two projective spaces. Therefore, for a point
$\pi ^{-1}(p)$ is a smooth Fano variety of Picard number two satisfying the condition (FLNT); by the induction hypothesis it is a product of two projective spaces. Therefore, for a point ![]() $p \in X_{1,2}$, we have
$p \in X_{1,2}$, we have ![]() $\mathcal {E}|_{g_1^{-1}(p)} \simeq \mathcal {O}(a)^{\oplus \operatorname {rank} \mathcal {E}}$. From the continuity of the first Chern class, the number
$\mathcal {E}|_{g_1^{-1}(p)} \simeq \mathcal {O}(a)^{\oplus \operatorname {rank} \mathcal {E}}$. From the continuity of the first Chern class, the number ![]() $a$ is independent from
$a$ is independent from ![]() $p \in X_{1,2}$. Thus, by tensoring
$p \in X_{1,2}$. Thus, by tensoring ![]() $\mathcal {E}$ with a line bundle, we may assume that
$\mathcal {E}$ with a line bundle, we may assume that ![]() $\mathcal {E}|_{g_1^{-1}(p)}$ is trivial for any point
$\mathcal {E}|_{g_1^{-1}(p)}$ is trivial for any point ![]() $p \in X_{1,2}$. By Grauert's theorem [Reference HartshorneHar77, III. Corollary 12.9], we see that
$p \in X_{1,2}$. By Grauert's theorem [Reference HartshorneHar77, III. Corollary 12.9], we see that ![]() ${g_1}_\ast (\mathcal {E})$ is a vector bundle on
${g_1}_\ast (\mathcal {E})$ is a vector bundle on ![]() $X_{1,2}$. Then it is straightforward to verify that the natural map
$X_{1,2}$. Then it is straightforward to verify that the natural map ![]() ${g_1}^{\ast }({g_1}_\ast (\mathcal {E})) \to \mathcal {E}$ is an isomorphism via Nakayama's lemma. Thus, we have
${g_1}^{\ast }({g_1}_\ast (\mathcal {E})) \to \mathcal {E}$ is an isomorphism via Nakayama's lemma. Thus, we have
Again, by the inductive hypothesis, ![]() $X_1\cong \prod _{j=1}^{\rho _X-1} \mathbb {P}^{n_j}$ and
$X_1\cong \prod _{j=1}^{\rho _X-1} \mathbb {P}^{n_j}$ and ![]() $X_{1,2}\cong \prod _{j=2}^{\rho _X-1} \mathbb {P}^{n_j}$; we also see that
$X_{1,2}\cong \prod _{j=2}^{\rho _X-1} \mathbb {P}^{n_j}$; we also see that ![]() $X_1 \to X_{1,2}$ is a natural projection. This concludes that
$X_1 \to X_{1,2}$ is a natural projection. This concludes that ![]() $X$ is isomorphic to
$X$ is isomorphic to ![]() $\mathbb {P}^{n_1}\times \mathbb {P}({g_1}_\ast (\mathcal {E}))$. Since
$\mathbb {P}^{n_1}\times \mathbb {P}({g_1}_\ast (\mathcal {E}))$. Since ![]() $\mathbb {P}({g_1}_\ast (\mathcal {E}))$ is a product of projective spaces, our assertion holds.
$\mathbb {P}({g_1}_\ast (\mathcal {E}))$ is a product of projective spaces, our assertion holds.
Corollary 7.7 (Structure theorem of FLNT varieties)
Let ![]() $X$ be a smooth projective variety satisfying the condition (FLNT). Then there exists a
$X$ be a smooth projective variety satisfying the condition (FLNT). Then there exists a ![]() $K_X$-negative contraction
$K_X$-negative contraction ![]() $\varphi \colon X \to M$ which satisfy the following properties:
$\varphi \colon X \to M$ which satisfy the following properties:
(1)
 $M$ is an étale quotient of an ordinary abelian variety
$M$ is an étale quotient of an ordinary abelian variety  $A$;.
$A$;.(2)
 $\varphi$ is a smooth morphism whose fibers are isomorphic to a product of projective spaces.
$\varphi$ is a smooth morphism whose fibers are isomorphic to a product of projective spaces.
In particular, there exist a finite étale cover ![]() $Y \to X$ and a smooth contraction
$Y \to X$ and a smooth contraction ![]() $f \colon Y \to A$ onto an ordinary abelian variety
$f \colon Y \to A$ onto an ordinary abelian variety ![]() $A$ such that all
$A$ such that all ![]() $f$-fibers are isomorphic to a product of projective spaces.
$f$-fibers are isomorphic to a product of projective spaces.
Proof. By Theorem 1.8, ![]() $X$ admits a smooth fibration
$X$ admits a smooth fibration ![]() $\varphi \colon X \to M$ such that all fibers are smooth Fano varieties and the tangent bundle of
$\varphi \colon X \to M$ such that all fibers are smooth Fano varieties and the tangent bundle of ![]() $M$ is numerically flat. Since Corollary 1.4 implies that
$M$ is numerically flat. Since Corollary 1.4 implies that ![]() $H^1(F, \mathcal {O}_F) = 0$ for all fiber
$H^1(F, \mathcal {O}_F) = 0$ for all fiber ![]() $F$ of
$F$ of ![]() $\varphi$, we have
$\varphi$, we have ![]() $R^1\varphi _* \mathcal {O}_X =0$. Hence, all fibers
$R^1\varphi _* \mathcal {O}_X =0$. Hence, all fibers ![]() $F$ and the image
$F$ and the image ![]() $M$ are
$M$ are ![]() $F$-liftable by Proposition 7.2. In particular,
$F$-liftable by Proposition 7.2. In particular, ![]() $F$ is isomorphic to a product of projective spaces and
$F$ is isomorphic to a product of projective spaces and ![]() $M$ is an étale quotient of an ordinary abelian variety
$M$ is an étale quotient of an ordinary abelian variety ![]() $A$.
$A$.
Set ![]() $Y := X \times _M A$ and let
$Y := X \times _M A$ and let ![]() $f \colon Y \to A$ be the natural projection. Then the last assertion follows.
$f \colon Y \to A$ be the natural projection. Then the last assertion follows.
Proof of Theorem 1.12 By Corollary 7.7, there exist a finite étale cover ![]() $\tau _1\colon Y_1 \to X$ and a smooth
$\tau _1\colon Y_1 \to X$ and a smooth ![]() $(\prod \mathbb {P}^{n_i})$-fibration
$(\prod \mathbb {P}^{n_i})$-fibration ![]() $f_1\colon Y_1 \to A_1$ over an ordinary abelian variety. We may find a finite étale cover
$f_1\colon Y_1 \to A_1$ over an ordinary abelian variety. We may find a finite étale cover ![]() $\tau _2\colon Y \to Y_1$ such that the composite
$\tau _2\colon Y \to Y_1$ such that the composite ![]() $Y \to Y_1 \to X$ is an étale Galois cover (see, for instance, [Reference SzamuelySza09, Proposition 5.3.9]). We denote the Albanese morphism by
$Y \to Y_1 \to X$ is an étale Galois cover (see, for instance, [Reference SzamuelySza09, Proposition 5.3.9]). We denote the Albanese morphism by ![]() $\alpha := \alpha _{Y} \colon Y \to A := \operatorname {Alb}(Y)$. By the universal property of the Albanese variety, we obtain a morphism
$\alpha := \alpha _{Y} \colon Y \to A := \operatorname {Alb}(Y)$. By the universal property of the Albanese variety, we obtain a morphism ![]() $\tau _3 \colon A \to A_1$ which satisfies the following commutative diagram.
$\tau _3 \colon A \to A_1$ which satisfies the following commutative diagram.

Here we prove that ![]() $\tau _3$ is étale. All
$\tau _3$ is étale. All ![]() $f_1$-fibers are isomorphic to
$f_1$-fibers are isomorphic to ![]() $\prod \mathbb {P}^{n_i}$ and, hence, algebraically simply connected. Thus each
$\prod \mathbb {P}^{n_i}$ and, hence, algebraically simply connected. Thus each ![]() $f_1 \circ \tau _2$-fiber is a disjoint union of
$f_1 \circ \tau _2$-fiber is a disjoint union of ![]() $\prod \mathbb {P}^{n_i}$. In particular,
$\prod \mathbb {P}^{n_i}$. In particular, ![]() $f_1 \circ \tau _2$-fibers are contracted by
$f_1 \circ \tau _2$-fibers are contracted by ![]() $\alpha$. Therefore,
$\alpha$. Therefore, ![]() $\tau _3$ is finite. Since
$\tau _3$ is finite. Since ![]() $f_1 \circ \tau _2$ is surjective, the morphism
$f_1 \circ \tau _2$ is surjective, the morphism ![]() $\tau _3$ is also surjective. In particular,
$\tau _3$ is also surjective. In particular, ![]() $\tau _3$ is a finite surjective morphism between abelian varieties. This, in turn, implies that
$\tau _3$ is a finite surjective morphism between abelian varieties. This, in turn, implies that ![]() $\alpha$ is surjective with equidimensional fibers. Thus,
$\alpha$ is surjective with equidimensional fibers. Thus, ![]() $\alpha$ is flat. Since
$\alpha$ is flat. Since ![]() $\tau _3 \circ \alpha$ is smooth,
$\tau _3 \circ \alpha$ is smooth, ![]() $\tau _3$ is étale.
$\tau _3$ is étale.
Since ![]() $\tau _3$ is étale and
$\tau _3$ is étale and ![]() $\tau _3 \circ \alpha$ is smooth, the morphism
$\tau _3 \circ \alpha$ is smooth, the morphism ![]() $\alpha$ is smooth. Thus, it is enough to show that
$\alpha$ is smooth. Thus, it is enough to show that ![]() $\alpha$-fibers are connected. To prove this, let us consider the Stein factorization
$\alpha$-fibers are connected. To prove this, let us consider the Stein factorization ![]() $Y \xrightarrow {q_1} A' \xrightarrow {q_2} A$, where
$Y \xrightarrow {q_1} A' \xrightarrow {q_2} A$, where ![]() $q_1$ is a contraction and
$q_1$ is a contraction and ![]() $q_2$ is a finite morphism. Since
$q_2$ is a finite morphism. Since ![]() $q_2$ is étale,
$q_2$ is étale, ![]() $A'$ is an abelian variety (see, for instance, [Reference MumfordMum70, Section 18]). This implies that
$A'$ is an abelian variety (see, for instance, [Reference MumfordMum70, Section 18]). This implies that ![]() $q_1\colon Y \to A'$ factors through
$q_1\colon Y \to A'$ factors through ![]() $\alpha \colon Y \to A$, that is, there exists a morphism
$\alpha \colon Y \to A$, that is, there exists a morphism ![]() $\beta \colon A\to A'$ such that
$\beta \colon A\to A'$ such that ![]() $q_1 =\beta \circ \alpha$. By virtue of the universality of
$q_1 =\beta \circ \alpha$. By virtue of the universality of ![]() $A$ and the rigidity lemma [Reference DebarreDeb01, Lemma 1.15] for
$A$ and the rigidity lemma [Reference DebarreDeb01, Lemma 1.15] for ![]() $q_1$, we see that
$q_1$, we see that ![]() $\beta$ is an isomorphism and the assertion follows.
$\beta$ is an isomorphism and the assertion follows.
Acknowledgements
The content of this article was first planned as a collaborative work of these authors with Doctor Sho Ejiri, who has refrained from being listed as a coauthor for the reason that he did not think his contribution was sufficient. Nevertheless, we are greatly indebted to him for sharing ideas and discussions about the subject, especially about the case of numerically flat tangent bundles and about the Frobenius splitting methods; we wish to express our sincere gratitude to him.
The first author would like to thank Dr T. Kawakami for helpful discussions.
Conflicts of Interest
None.