The classical Poitou–Tate theorem considers the cohomology of Galois groups with restricted ramification of global fields. It states a perfect duality between Shafarevich–Tate groups, and a
![]() $9$
-term exact sequence relating global and local cohomology groups, cf. [Reference Neukirch, Schmidt and WingbergNSW08, (8.6.7), (8.6.10)]. We prove the following generalization to higher dimensional schemes (see § 1 for the notation).
$9$
-term exact sequence relating global and local cohomology groups, cf. [Reference Neukirch, Schmidt and WingbergNSW08, (8.6.7), (8.6.10)]. We prove the following generalization to higher dimensional schemes (see § 1 for the notation).
Let
![]() $S$
be a non-empty set of places of a global field
$S$
be a non-empty set of places of a global field
![]() $k$
, and assume that
$k$
, and assume that
![]() $S$
contains the set
$S$
contains the set
![]() $S_{\infty }$
of archimedean places if
$S_{\infty }$
of archimedean places if
![]() $k$
is a number field. Let
$k$
is a number field. Let
![]() ${\mathcal{O}}_{S}$
be the ring of
${\mathcal{O}}_{S}$
be the ring of
![]() $S$
-integers in
$S$
-integers in
![]() $k$
and
$k$
and
![]() $\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
. Let
$\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
. Let
![]() $\mathscr{X}\rightarrow \mathscr{S}$
be a regular, flat, and separated scheme of finite type of relative dimension
$\mathscr{X}\rightarrow \mathscr{S}$
be a regular, flat, and separated scheme of finite type of relative dimension
![]() $r$
,
$r$
,
![]() $m\geqslant 1$
an integer invertible on
$m\geqslant 1$
an integer invertible on
![]() $\mathscr{S}$
and
$\mathscr{S}$
and
![]() $\mathscr{F}$
a locally constant, constructible sheaf of
$\mathscr{F}$
a locally constant, constructible sheaf of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{X}$
. We consider the Shafarevich–Tate groups defined by
$\mathscr{X}$
. We consider the Shafarevich–Tate groups defined by
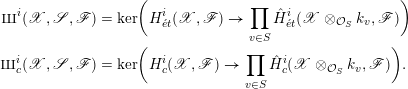 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0428}^{i}(\mathscr{X},\mathscr{S},\mathscr{F}) & = & \displaystyle \ker \biggl(H_{\acute{e} t}^{i}(\mathscr{X},\mathscr{F})\rightarrow \mathop{\prod }_{v\in S}{\hat{H}}_{\acute{e} t}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})\biggr)\nonumber\\ \displaystyle \unicode[STIX]{x0428}_{c}^{i}(\mathscr{X},\mathscr{S},\mathscr{F}) & = & \displaystyle \ker \biggl(H_{c}^{i}(\mathscr{X},\mathscr{F})\rightarrow \mathop{\prod }_{v\in S}{\hat{H}}_{c}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0428}^{i}(\mathscr{X},\mathscr{S},\mathscr{F}) & = & \displaystyle \ker \biggl(H_{\acute{e} t}^{i}(\mathscr{X},\mathscr{F})\rightarrow \mathop{\prod }_{v\in S}{\hat{H}}_{\acute{e} t}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})\biggr)\nonumber\\ \displaystyle \unicode[STIX]{x0428}_{c}^{i}(\mathscr{X},\mathscr{S},\mathscr{F}) & = & \displaystyle \ker \biggl(H_{c}^{i}(\mathscr{X},\mathscr{F})\rightarrow \mathop{\prod }_{v\in S}{\hat{H}}_{c}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})\biggr).\nonumber\end{eqnarray}$$
Theorem A (Poitou–Tate duality).
Under the assumptions above, the Shafarevich–Tate groups are finite and there are perfect pairings for
![]() $i=0,\ldots ,2r+2$
:
$i=0,\ldots ,2r+2$
:
Recall that a homomorphism
![]() $\unicode[STIX]{x1D711}:A\rightarrow B$
between topological groups is strict if it is continuous and the isomorphism
$\unicode[STIX]{x1D711}:A\rightarrow B$
between topological groups is strict if it is continuous and the isomorphism
![]() $A/\!\ker (\unicode[STIX]{x1D711})\stackrel{{\sim}}{\rightarrow }\text{im}(\unicode[STIX]{x1D711})\subset B$
is a homeomorphism. It is called proper if preimages of compact sets are compact.
$A/\!\ker (\unicode[STIX]{x1D711})\stackrel{{\sim}}{\rightarrow }\text{im}(\unicode[STIX]{x1D711})\subset B$
is a homeomorphism. It is called proper if preimages of compact sets are compact.
Theorem B (Poitou–Tate exact sequence).
For
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $\mathscr{S}$
and
$\mathscr{S}$
and
![]() $\mathscr{F}$
as above, we have an exact
$\mathscr{F}$
as above, we have an exact
![]() $6r+9$
-term sequence of abelian topological groups and strict homomorphisms
$6r+9$
-term sequence of abelian topological groups and strict homomorphisms
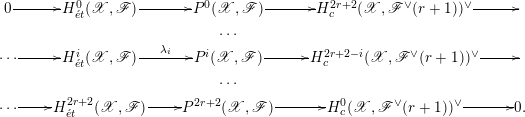
Here
is the restricted product with respect to the subgroups
![]() $H_{\mathit{nr}}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})$
(see Definition 6.6). The localization map
$H_{\mathit{nr}}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})$
(see Definition 6.6). The localization map
![]() $\unicode[STIX]{x1D706}_{i}$
is proper and has finite kernel for all
$\unicode[STIX]{x1D706}_{i}$
is proper and has finite kernel for all
![]() $i$
, and for
$i$
, and for
![]() $i\geqslant 2r+3$
,
$i\geqslant 2r+3$
,
is an isomorphism. The groups in the left column of (0.2) are discrete, those in the middle column locally compact, and those in the right column compact.
If
![]() $\mathscr{X}$
is a smooth variety over
$\mathscr{X}$
is a smooth variety over
![]() $k$
(i.e.,
$k$
(i.e.,
![]() $S=$
all places), Theorem B was proven by Saito [Reference SaitoSai89]. His proof combines classical Poitou–Tate duality with the fact that
$S=$
all places), Theorem B was proven by Saito [Reference SaitoSai89]. His proof combines classical Poitou–Tate duality with the fact that
![]() $Rf^{!}(\unicode[STIX]{x2124}/m\unicode[STIX]{x2124})\cong \unicode[STIX]{x1D707}_{m}^{\otimes d}[2d]$
for any smooth, geometrically connected morphism
$Rf^{!}(\unicode[STIX]{x2124}/m\unicode[STIX]{x2124})\cong \unicode[STIX]{x1D707}_{m}^{\otimes d}[2d]$
for any smooth, geometrically connected morphism
![]() $f:X\rightarrow Y$
of schemes with
$f:X\rightarrow Y$
of schemes with
![]() $m$
invertible on
$m$
invertible on
![]() $Y$
[Reference Artin, Grothendieck and VerdierSGA4, XVIII Theorem (3.2.5)]. With mild effort, Saito’s argument can be extended to the case that
$Y$
[Reference Artin, Grothendieck and VerdierSGA4, XVIII Theorem (3.2.5)]. With mild effort, Saito’s argument can be extended to the case that
![]() $\mathscr{X}\rightarrow \mathscr{S}$
is smooth. The essential new achievement of this paper is that the assumption on
$\mathscr{X}\rightarrow \mathscr{S}$
is smooth. The essential new achievement of this paper is that the assumption on
![]() $\mathscr{X}$
can be weakened from smooth to regular. We overcome the technical difficulty with
$\mathscr{X}$
can be weakened from smooth to regular. We overcome the technical difficulty with
![]() $Rf^{!}$
by making a detour to algebraic cycle complexes, which have good base change properties by [Reference GeisserGei10]. Furthermore, we prove a compactly supported version of Theorem B and a version that applies to singular schemes and non-invertible coefficients as well.
$Rf^{!}$
by making a detour to algebraic cycle complexes, which have good base change properties by [Reference GeisserGei10]. Furthermore, we prove a compactly supported version of Theorem B and a version that applies to singular schemes and non-invertible coefficients as well.
In our context it is technically more convenient to work with henselizations rather than completions. Therefore we will first prove our results in their henselian versions and will pass to completions in the final § 10.
1 Notation and conventions
In this paper we use the following notation:
–
 $k$
a global field,
$k$
a global field,
 $p=\text{char}(k)$
;
$p=\text{char}(k)$
;–
 $k_{v}$
(respectively
$k_{v}$
(respectively
 $k_{(v)}$
) the completion (respectively henselization) of
$k_{(v)}$
) the completion (respectively henselization) of
 $k$
at a place
$k$
at a place
 $v$
;
$v$
;–
 ${\mathcal{O}}_{v}$
(respectively
${\mathcal{O}}_{v}$
(respectively
 ${\mathcal{O}}_{(v)}$
) the ring of integers of
${\mathcal{O}}_{(v)}$
) the ring of integers of
 $k_{v}$
(respectively of
$k_{v}$
(respectively of
 $k_{(v)}$
) (if
$k_{(v)}$
) (if
 $v$
is non-archimedean);
$v$
is non-archimedean);–
 $S_{\infty }$
the set of archimedean places if
$S_{\infty }$
the set of archimedean places if
 $k$
is a number field (
$k$
is a number field (
 $S_{\infty }=\varnothing$
otherwise);
$S_{\infty }=\varnothing$
otherwise);–
 $S_{\unicode[STIX]{x211D}}\subset S_{\infty }$
the set of real places;
$S_{\unicode[STIX]{x211D}}\subset S_{\infty }$
the set of real places;–
 $S$
a set of places of
$S$
a set of places of
 $k$
containing
$k$
containing
 $S_{\infty }$
;
$S_{\infty }$
;–
 ${\mathcal{O}}_{S}$
the ring of
${\mathcal{O}}_{S}$
the ring of
 $S$
-integers in
$S$
-integers in
 $k$
(if
$k$
(if
 $S\neq \varnothing$
);
$S\neq \varnothing$
);–
 $\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
, if
$\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
, if
 $p>0$
and
$p>0$
and
 $S=\varnothing$
, then
$S=\varnothing$
, then
 $\mathscr{S}$
is the unique regular, complete curve with function field
$\mathscr{S}$
is the unique regular, complete curve with function field
 $k$
;
$k$
;–
 $\mathscr{X}\rightarrow \mathscr{S}$
a separated scheme of finite type over
$\mathscr{X}\rightarrow \mathscr{S}$
a separated scheme of finite type over
 $\mathscr{S}$
;
$\mathscr{S}$
;–
 $X_{v}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v}$
for a place
$X_{v}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v}$
for a place
 $v$
of
$v$
of
 $k$
, analogous:
$k$
, analogous:
 $X_{(v)}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{(v)}$
;
$X_{(v)}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{(v)}$
;–
 $\mathscr{X}_{v}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{v}$
for a non-archimedean place
$\mathscr{X}_{v}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{v}$
for a non-archimedean place
 $v$
of
$v$
of
 $k$
;
$k$
;
 $\mathscr{X}_{(v)}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{(v)}$
;
$\mathscr{X}_{(v)}=\mathscr{X}\otimes _{{\mathcal{O}}_{S}}{\mathcal{O}}_{(v)}$
;–
 $A^{\vee }$
the Pontryagin dual of a locally compact abelian group;
$A^{\vee }$
the Pontryagin dual of a locally compact abelian group;–
 $\prod _{i\in I}(A_{i},B_{i})$
the restricted product of a family
$\prod _{i\in I}(A_{i},B_{i})$
the restricted product of a family
 $(A_{i})_{i\in I}$
of abelian Hausdorff topological groups with respect to open subgroups
$(A_{i})_{i\in I}$
of abelian Hausdorff topological groups with respect to open subgroups
 $B_{i}\subset A_{i}$
given for almost all
$B_{i}\subset A_{i}$
given for almost all
 $i\in I$
(the
$i\in I$
(the
 $B_{i}$
are omitted when clear from the context);
$B_{i}$
are omitted when clear from the context);–
 $m$
a natural number invertible on
$m$
a natural number invertible on
 $\mathscr{S}$
;
$\mathscr{S}$
;–
 $\mathscr{F}$
an étale sheaf of
$\mathscr{F}$
an étale sheaf of
 $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
 $\mathscr{X}_{\acute{e} t}$
;
$\mathscr{X}_{\acute{e} t}$
;–
 $\mathscr{F}^{\vee }(r)$
the
$\mathscr{F}^{\vee }(r)$
the
 $r$
th Tate twist of the dual sheaf
$r$
th Tate twist of the dual sheaf
 ${\mathcal{H}}\!\mathit{om}(\mathscr{F},\unicode[STIX]{x2124}/m\unicode[STIX]{x2124})$
;
${\mathcal{H}}\!\mathit{om}(\mathscr{F},\unicode[STIX]{x2124}/m\unicode[STIX]{x2124})$
;–
 $X_{\acute{e} t}$
the small étale site of a scheme
$X_{\acute{e} t}$
the small étale site of a scheme
 $X$
;
$X$
;–
 $H_{\acute{e} t}^{\ast }(X,-)$
the étale cohomology
$H_{\acute{e} t}^{\ast }(X,-)$
the étale cohomology
 $X$
;
$X$
;–
 $H_{c}^{\ast }(X,-)$
the étale cohomology with compact support of a scheme
$H_{c}^{\ast }(X,-)$
the étale cohomology with compact support of a scheme
 $X$
, separated and of finite type over some base scheme
$X$
, separated and of finite type over some base scheme
 $B$
.
$B$
.
If
![]() $v$
is non-archimedean and the fibre of
$v$
is non-archimedean and the fibre of
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $v$
is empty, then
$v$
is empty, then
![]() $X_{v}\rightarrow \mathscr{X}_{v}$
is a scheme isomorphism. However,
$X_{v}\rightarrow \mathscr{X}_{v}$
is a scheme isomorphism. However,
![]() $H_{c}^{\ast }(X_{v},-)$
and
$H_{c}^{\ast }(X_{v},-)$
and
![]() $H_{c}^{\ast }(\mathscr{X}_{v},-)$
differ because the base scheme is different.
$H_{c}^{\ast }(\mathscr{X}_{v},-)$
differ because the base scheme is different.
The modification of a cohomology theory
![]() $H^{\ast }$
with respect to the real places is denoted by
$H^{\ast }$
with respect to the real places is denoted by
![]() ${\hat{H}}^{\ast }$
, see § 2.
${\hat{H}}^{\ast }$
, see § 2.
For a scheme
![]() $X$
, we denote by
$X$
, we denote by
![]() $\text{Sh}(X_{\acute{e} t})$
the category of sheaves of abelian groups on the small étale site on
$\text{Sh}(X_{\acute{e} t})$
the category of sheaves of abelian groups on the small étale site on
![]() $X$
. We call a complex
$X$
. We call a complex
![]() $\mathscr{F}^{\bullet }$
of sheaves in
$\mathscr{F}^{\bullet }$
of sheaves in
![]() $\text{Sh}(X_{\acute{e} t})$
bounded if almost all of its cohomology sheaves are zero. We call
$\text{Sh}(X_{\acute{e} t})$
bounded if almost all of its cohomology sheaves are zero. We call
![]() $\mathscr{F}^{\bullet }$
locally constant, torsion, constructible, etc., if all cohomology sheaves have this property.
$\mathscr{F}^{\bullet }$
locally constant, torsion, constructible, etc., if all cohomology sheaves have this property.
2 Modified cohomology
In this section we extend the definition of the modified (or ‘compactly supported’) étale cohomology of an étale sheaf on a number ring defined by Zink [Reference ZinkZin78] to bounded complexes of sheaves. Our construction involves a cone. As a cone is only well defined for an actual morphism of complexes (and not for a morphism in the derived category), we work with Godement resolutions to obtain a functorial model for hypercohomology.
Let
![]() $G$
be a finite group and let
$G$
be a finite group and let
![]() $A$
be a
$A$
be a
![]() $G$
-module. We let
$G$
-module. We let
![]() $A^{\text{tr}}$
be the trivial
$A^{\text{tr}}$
be the trivial
![]() $G$
-module with underlying abelian group
$G$
-module with underlying abelian group
![]() $A$
and
$A$
and
![]() $A_{1}:=\operatorname{coker}(\unicode[STIX]{x1D704}:A\rightarrow \operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}})$
, where
$A_{1}:=\operatorname{coker}(\unicode[STIX]{x1D704}:A\rightarrow \operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}})$
, where
![]() $\operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}}$
is the induced module
$\operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}}$
is the induced module
![]() $\bigoplus _{\unicode[STIX]{x1D70E}\in G}A_{\unicode[STIX]{x1D70E}}^{\text{tr}}$
(on which
$\bigoplus _{\unicode[STIX]{x1D70E}\in G}A_{\unicode[STIX]{x1D70E}}^{\text{tr}}$
(on which
![]() $G$
acts by interchanging the summands) and
$G$
acts by interchanging the summands) and
![]() $\unicode[STIX]{x1D704}(a)=(\unicode[STIX]{x1D70E}a)_{\unicode[STIX]{x1D70E}}$
. We set
$\unicode[STIX]{x1D704}(a)=(\unicode[STIX]{x1D70E}a)_{\unicode[STIX]{x1D70E}}$
. We set
![]() $A_{0}=A$
and recursively
$A_{0}=A$
and recursively
![]() $A_{n+1}:=(A_{n})_{1}$
for
$A_{n+1}:=(A_{n})_{1}$
for
![]() $n\geqslant 0$
to obtain a functorial resolution
$n\geqslant 0$
to obtain a functorial resolution
of
![]() $A$
by induced, hence cohomologically trivial
$A$
by induced, hence cohomologically trivial
![]() $G$
-modules. Hence the hypercohomology
$G$
-modules. Hence the hypercohomology
![]() $\unicode[STIX]{x210D}(G,A)$
is naturally isomorphic to
$\unicode[STIX]{x210D}(G,A)$
is naturally isomorphic to
![]() $C^{\bullet }(A)^{G}$
.
$C^{\bullet }(A)^{G}$
.
If
![]() $G=\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
, we can interpret
$G=\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
, we can interpret
![]() $G$
-modules as sheaves on
$G$
-modules as sheaves on
![]() $(\operatorname{Spec}\unicode[STIX]{x211D})_{\acute{e} t}$
and (2.1) is nothing but the Godement resolution
$(\operatorname{Spec}\unicode[STIX]{x211D})_{\acute{e} t}$
and (2.1) is nothing but the Godement resolution
which is defined by
![]() $C^{n}(\mathscr{F})=i_{\ast }i^{\ast }\mathscr{F}_{n}$
with
$C^{n}(\mathscr{F})=i_{\ast }i^{\ast }\mathscr{F}_{n}$
with
![]() $i:\operatorname{Spec}\unicode[STIX]{x2102}\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
the canonical morphism and
$i:\operatorname{Spec}\unicode[STIX]{x2102}\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
the canonical morphism and
![]() $\mathscr{F}_{0}=\mathscr{F}$
,
$\mathscr{F}_{0}=\mathscr{F}$
,
![]() $\mathscr{F}_{n+1}:=\operatorname{coker}(\mathscr{F}_{n}\rightarrow i_{\ast }i^{\ast }\mathscr{F}_{n})$
, cf. [Reference MilneMil80, III, 1.20].
$\mathscr{F}_{n+1}:=\operatorname{coker}(\mathscr{F}_{n}\rightarrow i_{\ast }i^{\ast }\mathscr{F}_{n})$
, cf. [Reference MilneMil80, III, 1.20].
Returning to the case of a general finite group
![]() $G$
, let
$G$
, let
![]() $A_{-1}=\ker (\unicode[STIX]{x1D700}:\operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}}\rightarrow A)$
with
$A_{-1}=\ker (\unicode[STIX]{x1D700}:\operatorname{Ind}_{G}^{\{1\}}A^{\text{tr}}\rightarrow A)$
with
![]() $\unicode[STIX]{x1D700}(a_{\unicode[STIX]{x1D70E}})=\sum \unicode[STIX]{x1D70E}^{-1}a_{\unicode[STIX]{x1D70E}}$
. We put
$\unicode[STIX]{x1D700}(a_{\unicode[STIX]{x1D70E}})=\sum \unicode[STIX]{x1D70E}^{-1}a_{\unicode[STIX]{x1D70E}}$
. We put
![]() $A_{0}=A$
and recursively
$A_{0}=A$
and recursively
![]() $A_{n-1}:=(A_{n})_{-1}$
for
$A_{n-1}:=(A_{n})_{-1}$
for
![]() $n\leqslant 0$
to obtain a left resolution
$n\leqslant 0$
to obtain a left resolution
We splice these resolutions together to obtain a functorial complete acyclic resolution
![]() ${\hat{C}}^{\bullet }(A)$
of
${\hat{C}}^{\bullet }(A)$
of
![]() $A$
$A$
which calculates Tate cohomology:
![]() ${\hat{H}}^{n}(G,A)=H^{n}({\hat{C}}^{\bullet }(A)^{G})$
,
${\hat{H}}^{n}(G,A)=H^{n}({\hat{C}}^{\bullet }(A)^{G})$
,
![]() $n\in \unicode[STIX]{x2124}$
.
$n\in \unicode[STIX]{x2124}$
.
Definition 2.1. Let
![]() $G$
be a finite group and let
$G$
be a finite group and let
![]() $A^{\bullet }$
be a bounded complex of
$A^{\bullet }$
be a bounded complex of
![]() $G$
-modules. We put
$G$
-modules. We put
For a bounded complex
![]() $A^{\bullet }$
the spectral sequence of the double complex
$A^{\bullet }$
the spectral sequence of the double complex
![]() ${\hat{C}}^{\bullet }(A^{\bullet })^{G}$
${\hat{C}}^{\bullet }(A^{\bullet })^{G}$
converges. Hence for an exact bounded complex
![]() $A^{\bullet }$
also the complex
$A^{\bullet }$
also the complex
![]() $\hat{\unicode[STIX]{x210D}}(A^{\bullet })$
is exact. Moreover, the assignment
$\hat{\unicode[STIX]{x210D}}(A^{\bullet })$
is exact. Moreover, the assignment
![]() $A^{\bullet }\mapsto \hat{\unicode[STIX]{x210D}}(G,A^{\bullet })$
commutes with the operation of taking the cone of a complex homomorphism. We therefore obtain a functor ‘Tate cohomology’ on
$A^{\bullet }\mapsto \hat{\unicode[STIX]{x210D}}(G,A^{\bullet })$
commutes with the operation of taking the cone of a complex homomorphism. We therefore obtain a functor ‘Tate cohomology’ on
![]() $\mathscr{D}^{b}(G\text{-Mod})$
, the derived category of bounded complexes of
$\mathscr{D}^{b}(G\text{-Mod})$
, the derived category of bounded complexes of
![]() $G$
-modules. For a single
$G$
-modules. For a single
![]() $G$
-module
$G$
-module
![]() $A$
considered as a complex concentrated in degree zero this gives back the usual Tate cohomology. Note that the natural map
$A$
considered as a complex concentrated in degree zero this gives back the usual Tate cohomology. Note that the natural map
![]() $C^{\bullet }(A)\rightarrow {\hat{C}}^{\bullet }(A)$
induces a map
$C^{\bullet }(A)\rightarrow {\hat{C}}^{\bullet }(A)$
induces a map
![]() $\unicode[STIX]{x210D}(G,A^{\bullet })\rightarrow \hat{\unicode[STIX]{x210D}}(G,A^{\bullet })$
.
$\unicode[STIX]{x210D}(G,A^{\bullet })\rightarrow \hat{\unicode[STIX]{x210D}}(G,A^{\bullet })$
.
If
![]() $G=\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
, we can translate this definition into the language of sheaves and obtain the modified (hyper) cohomology
$G=\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
, we can translate this definition into the language of sheaves and obtain the modified (hyper) cohomology
for any bounded complex
![]() $\mathscr{F}^{\bullet }$
of sheaves on
$\mathscr{F}^{\bullet }$
of sheaves on
![]() $(\operatorname{Spec}\unicode[STIX]{x211D})_{\acute{e} t}$
. We have the hypercohomology spectral sequence
$(\operatorname{Spec}\unicode[STIX]{x211D})_{\acute{e} t}$
. We have the hypercohomology spectral sequence
Definition 2.2. Let
![]() $f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
be a separated scheme of finite type and let
$f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
be a separated scheme of finite type and let
![]() $\mathscr{F}^{\bullet }$
be a bounded complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded complex of sheaves on
![]() $X_{\acute{e} t}$
. We define the modified étale hypercohomology by
$X_{\acute{e} t}$
. We define the modified étale hypercohomology by
and put
If
![]() $\mathscr{F}^{\bullet }$
is torsion, we define the modified étale hypercohomology with compact support by
$\mathscr{F}^{\bullet }$
is torsion, we define the modified étale hypercohomology with compact support by
and put
Note that this makes sense since
![]() $Rf_{\ast }\mathscr{F}^{\bullet },Rf_{!}\mathscr{F}^{\bullet }\in \mathscr{D}^{b}(\text{Sh}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x211D}))$
.
$Rf_{\ast }\mathscr{F}^{\bullet },Rf_{!}\mathscr{F}^{\bullet }\in \mathscr{D}^{b}(\text{Sh}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x211D}))$
.
We will also modify the Ext-groups. Let
![]() $f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
be a separated scheme of finite type and
$f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
be a separated scheme of finite type and
![]() $\mathscr{F}^{\bullet }$
,
$\mathscr{F}^{\bullet }$
,
![]() $\mathscr{G}^{\bullet }$
complexes of sheaves on
$\mathscr{G}^{\bullet }$
complexes of sheaves on
![]() $X_{\acute{e} t}$
. Recall that
$X_{\acute{e} t}$
. Recall that
Definition 2.3. If
![]() $R\,{\mathcal{H}}\!\mathit{om}(\mathscr{F}^{\bullet },\mathscr{G}^{\bullet })$
is bounded, we define
$R\,{\mathcal{H}}\!\mathit{om}(\mathscr{F}^{\bullet },\mathscr{G}^{\bullet })$
is bounded, we define
and put
Remark 2.4. Assume that
![]() $f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
factors through
$f:X\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
factors through
![]() $\operatorname{Spec}\unicode[STIX]{x2102}$
, i.e.,
$\operatorname{Spec}\unicode[STIX]{x2102}$
, i.e.,
![]() $f=ig$
with
$f=ig$
with
![]() $g:X\rightarrow \operatorname{Spec}\unicode[STIX]{x2102}$
and
$g:X\rightarrow \operatorname{Spec}\unicode[STIX]{x2102}$
and
![]() $i:\operatorname{Spec}\unicode[STIX]{x2102}\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
the canonical morphism. Then
$i:\operatorname{Spec}\unicode[STIX]{x2102}\rightarrow \operatorname{Spec}\unicode[STIX]{x211D}$
the canonical morphism. Then
![]() $Rf_{\ast }=i_{\ast }\circ Rg_{\ast }=\operatorname{Ind}_{\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})}^{\{1\}}\circ Rg_{\ast }$
and hence
$Rf_{\ast }=i_{\ast }\circ Rg_{\ast }=\operatorname{Ind}_{\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})}^{\{1\}}\circ Rg_{\ast }$
and hence
The same argument works for cohomology with compact support and for Ext-groups.
Notational convention. For a scheme
![]() $X$
over
$X$
over
![]() $\unicode[STIX]{x2102}$
, we put
$\unicode[STIX]{x2102}$
, we put
For a scheme
![]() $X$
over a non-archimedean local field, we put
$X$
over a non-archimedean local field, we put
i.e., the
![]() $\hat{\text{ }}$
is redundant. The same convention applies to cohomology with compact support and to Ext-groups.
$\hat{\text{ }}$
is redundant. The same convention applies to cohomology with compact support and to Ext-groups.
Next we consider the scheme
![]() $\operatorname{Spec}\unicode[STIX]{x2124}$
. The set
$\operatorname{Spec}\unicode[STIX]{x2124}$
. The set
![]() $\{\unicode[STIX]{x2124}\rightarrow \unicode[STIX]{x2102},~(\unicode[STIX]{x2124}\rightarrow \bar{\unicode[STIX]{x1D53D}}_{p})_{p\text{ prime}}\}$
of geometric points is conservative and we consider the associated Godement resolution of a sheaf
$\{\unicode[STIX]{x2124}\rightarrow \unicode[STIX]{x2102},~(\unicode[STIX]{x2124}\rightarrow \bar{\unicode[STIX]{x1D53D}}_{p})_{p\text{ prime}}\}$
of geometric points is conservative and we consider the associated Godement resolution of a sheaf
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $(\operatorname{Spec}\unicode[STIX]{x2124})_{\acute{e} t}$
:
$(\operatorname{Spec}\unicode[STIX]{x2124})_{\acute{e} t}$
:
We consider the composite
Definition 2.5. We define
For a bounded complex
![]() $\mathscr{F}^{\bullet }$
of sheaves on
$\mathscr{F}^{\bullet }$
of sheaves on
![]() $(\operatorname{Spec}\unicode[STIX]{x2124})_{\acute{e} t}$
, we obtain the double complex
$(\operatorname{Spec}\unicode[STIX]{x2124})_{\acute{e} t}$
, we obtain the double complex
![]() $\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
, which we also consider as a single complex via the total complex functor and set
$\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
, which we also consider as a single complex via the total complex functor and set
For a bounded complex
![]() $\mathscr{F}^{\bullet }$
of sheaves the spectral sequence of the double complex
$\mathscr{F}^{\bullet }$
of sheaves the spectral sequence of the double complex
![]() $\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
converges. Hence for an exact bounded complex
$\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
converges. Hence for an exact bounded complex
![]() $\mathscr{F}^{\bullet }$
the complex
$\mathscr{F}^{\bullet }$
the complex
![]() $\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
is still exact. Moreover, the assignment
$\hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
is still exact. Moreover, the assignment
![]() $\mathscr{F}^{\bullet }\mapsto \hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
commutes (up to a canonical isomorphism of complexes) with the operation of taking the cone. Therefore
$\mathscr{F}^{\bullet }\mapsto \hat{\unicode[STIX]{x210D}}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124},\mathscr{F}^{\bullet })$
commutes (up to a canonical isomorphism of complexes) with the operation of taking the cone. Therefore
![]() ${\hat{H}}_{\acute{e} t}^{n}(\operatorname{Spec}\unicode[STIX]{x2124},-)$
is a functor on
${\hat{H}}_{\acute{e} t}^{n}(\operatorname{Spec}\unicode[STIX]{x2124},-)$
is a functor on
![]() $\mathscr{D}^{b}(\text{Sh}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124}))$
and the following definition makes sense.
$\mathscr{D}^{b}(\text{Sh}_{\acute{e} t}(\operatorname{Spec}\unicode[STIX]{x2124}))$
and the following definition makes sense.
Definition 2.6. Let
![]() $f:\mathscr{X}\rightarrow \operatorname{Spec}\unicode[STIX]{x2124}$
be a separated scheme of finite type and
$f:\mathscr{X}\rightarrow \operatorname{Spec}\unicode[STIX]{x2124}$
be a separated scheme of finite type and
![]() $\mathscr{F}^{\bullet }$
a bounded complex of sheaves on
$\mathscr{F}^{\bullet }$
a bounded complex of sheaves on
![]() $X_{\acute{e} t}$
. We define the modified étale cohomology by
$X_{\acute{e} t}$
. We define the modified étale cohomology by
If
![]() $\dim \mathscr{X}=1$
or
$\dim \mathscr{X}=1$
or
![]() $\mathscr{F}^{\bullet }$
is torsion (i.e., if we have a well-defined functor
$\mathscr{F}^{\bullet }$
is torsion (i.e., if we have a well-defined functor
![]() $Rf_{!}$
), we define the modified étale cohomology with compact support by
$Rf_{!}$
), we define the modified étale cohomology with compact support by
For a single sheaf
![]() $\mathscr{F}$
and
$\mathscr{F}$
and
![]() $n<0$
, the groups
$n<0$
, the groups
![]() ${\hat{H}}_{\acute{e} t}^{n}(\mathscr{X},\mathscr{F})\cong {\hat{H}}_{\acute{e} t}^{n-1}(X_{\unicode[STIX]{x211D}},\mathscr{F})$
are
${\hat{H}}_{\acute{e} t}^{n}(\mathscr{X},\mathscr{F})\cong {\hat{H}}_{\acute{e} t}^{n-1}(X_{\unicode[STIX]{x211D}},\mathscr{F})$
are
![]() $2$
-torsion groups. In general, we have a long exact sequence
$2$
-torsion groups. In general, we have a long exact sequence
The maps
![]() $\unicode[STIX]{x1D711}_{n}$
are isomorphisms for all
$\unicode[STIX]{x1D711}_{n}$
are isomorphisms for all
![]() $n\in \unicode[STIX]{x2124}$
if
$n\in \unicode[STIX]{x2124}$
if
![]() $\mathscr{X}\rightarrow \operatorname{Spec}\unicode[STIX]{x2124}$
factors through
$\mathscr{X}\rightarrow \operatorname{Spec}\unicode[STIX]{x2124}$
factors through
![]() $\operatorname{Spec}\unicode[STIX]{x1D53D}_{p}$
for a prime number
$\operatorname{Spec}\unicode[STIX]{x1D53D}_{p}$
for a prime number
![]() $p$
, or over
$p$
, or over
![]() $\operatorname{Spec}{\mathcal{O}}_{k}$
for a totally imaginary number field
$\operatorname{Spec}{\mathcal{O}}_{k}$
for a totally imaginary number field
![]() $k$
(cf. Remark 2.4). The compact support variant of (2.12) is the long exact sequence
$k$
(cf. Remark 2.4). The compact support variant of (2.12) is the long exact sequence
If
![]() $\mathscr{X}=\operatorname{Spec}{\mathcal{O}}_{S}$
for a number field
$\mathscr{X}=\operatorname{Spec}{\mathcal{O}}_{S}$
for a number field
![]() $k$
and a finite set
$k$
and a finite set
![]() $S\supset S_{\infty }$
of places of
$S\supset S_{\infty }$
of places of
![]() $k$
, and if
$k$
, and if
![]() $\mathscr{F}$
is a single sheaf on
$\mathscr{F}$
is a single sheaf on
![]() $\mathscr{X}_{\acute{e} t}$
, then our groups
$\mathscr{X}_{\acute{e} t}$
, then our groups
![]() ${\hat{H}}_{\acute{e} t}^{\ast }(\mathscr{X},\mathscr{F})$
coincide with the modified étale cohomology groups defined in [Reference ZinkZin78].
${\hat{H}}_{\acute{e} t}^{\ast }(\mathscr{X},\mathscr{F})$
coincide with the modified étale cohomology groups defined in [Reference ZinkZin78].
Now let
![]() $k$
be a global field. For a place
$k$
be a global field. For a place
![]() $v$
of
$v$
of
![]() $k$
, we denote by
$k$
, we denote by
![]() $k_{(v)}$
the henselization of
$k_{(v)}$
the henselization of
![]() $k$
at
$k$
at
![]() $v$
. For a set
$v$
. For a set
![]() $S$
of places of
$S$
of places of
![]() $k$
we set
$k$
we set
![]() $\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
. If
$\mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
. If
![]() $p=\text{char}(k)>0$
we make the following conventions.
$p=\text{char}(k)>0$
we make the following conventions.
–
 $S_{\infty }=\varnothing$
.
$S_{\infty }=\varnothing$
.– ‘
 $\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
’ is the unique smooth, proper curve with function field
$\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
’ is the unique smooth, proper curve with function field
 $k$
.
$k$
.– Cohomology with compact support is defined with respect to the structure morphism to
 $\operatorname{Spec}\unicode[STIX]{x1D53D}_{p}$
.
$\operatorname{Spec}\unicode[STIX]{x1D53D}_{p}$
.– The modification symbol
 $\hat{\text{ }}$
is redundant.
$\hat{\text{ }}$
is redundant.
For sets of places
![]() $S\supset T\supset S_{\infty }$
and
$S\supset T\supset S_{\infty }$
and
![]() $\mathscr{T}=\operatorname{Spec}{\mathcal{O}}_{T}$
, we put
$\mathscr{T}=\operatorname{Spec}{\mathcal{O}}_{T}$
, we put
The following lemma compares the modified compact support cohomology with ordinary cohomology. It is interesting even for
![]() $S=T$
.
$S=T$
.
Lemma 2.7. Let
![]() $S\supset T\supset S_{\infty }$
be sets of places with
$S\supset T\supset S_{\infty }$
be sets of places with
![]() $T$
finite and
$T$
finite and
![]() $\mathscr{F}^{\bullet }$
a bounded complex of sheaves on
$\mathscr{F}^{\bullet }$
a bounded complex of sheaves on
![]() $\mathscr{T}_{\acute{e} t}$
. Then we have a long exact sequence
$\mathscr{T}_{\acute{e} t}$
. Then we have a long exact sequence
Proof. We can assume that
![]() $S$
is finite since the general case follows by passing to the direct limit over all finite
$S$
is finite since the general case follows by passing to the direct limit over all finite
![]() $S^{\prime }$
with
$S^{\prime }$
with
![]() $S\supset S^{\prime }\supset T$
. Put
$S\supset S^{\prime }\supset T$
. Put
![]() $\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
and let
$\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
and let
![]() $j:\mathscr{T}{\hookrightarrow}\mathscr{B}$
be the open immersion. Consider the following commutative diagram.
$j:\mathscr{T}{\hookrightarrow}\mathscr{B}$
be the open immersion. Consider the following commutative diagram.

The first and third row, as well as the second and third column are distinguished triangles by definition. Also the second row is distinguished: it is the excision triangle for
![]() $\mathscr{S}\subset \mathscr{B}$
and the complex
$\mathscr{S}\subset \mathscr{B}$
and the complex
![]() $j_{!}\mathscr{F}^{\bullet }$
. We conclude that the first column is distinguished. The lower left vertical arrow is zero since it factors through
$j_{!}\mathscr{F}^{\bullet }$
. We conclude that the first column is distinguished. The lower left vertical arrow is zero since it factors through
![]() $\unicode[STIX]{x210D}(\mathscr{S},\mathscr{F}^{\bullet })$
. Hence
$\unicode[STIX]{x210D}(\mathscr{S},\mathscr{F}^{\bullet })$
. Hence
Finally note that
and that
for
![]() $v\in T\smallsetminus S_{\infty }$
.◻
$v\in T\smallsetminus S_{\infty }$
.◻
3 The dualizing complex
In this section let
![]() $B$
be an integral, noetherian and regular scheme of Krull-dimension
$B$
be an integral, noetherian and regular scheme of Krull-dimension
![]() ${\leqslant}1$
.
${\leqslant}1$
.
Definition 3.1. For
![]() $f:X\rightarrow B$
integral, separated and of finite type, we put
$f:X\rightarrow B$
integral, separated and of finite type, we put
![]() $Y=\overline{f(X)}\subset B$
and define the (absolute) dimension of
$Y=\overline{f(X)}\subset B$
and define the (absolute) dimension of
![]() $X$
by
$X$
by
The dimension of
![]() $X$
coincides with its Krull-dimension if
$X$
coincides with its Krull-dimension if
![]() $X\rightarrow B$
is proper or if
$X\rightarrow B$
is proper or if
![]() $\dim B=0$
or if
$\dim B=0$
or if
![]() $\dim B=1$
and
$\dim B=1$
and
![]() $B$
has infinitely many closed points. It differs, for example, for
$B$
has infinitely many closed points. It differs, for example, for
![]() $X=\operatorname{Spec}\unicode[STIX]{x211A}_{p}$
considered as a scheme over
$X=\operatorname{Spec}\unicode[STIX]{x211A}_{p}$
considered as a scheme over
![]() $B=\operatorname{Spec}\unicode[STIX]{x2124}_{p}$
.
$B=\operatorname{Spec}\unicode[STIX]{x2124}_{p}$
.
For a scheme
![]() $X$
, separated and of finite type over
$X$
, separated and of finite type over
![]() $B$
and an integer
$B$
and an integer
![]() $n$
, let
$n$
, let
![]() $\unicode[STIX]{x2124}_{X}^{c}(n)$
be Bloch’s cycle complex of relative dimension
$\unicode[STIX]{x2124}_{X}^{c}(n)$
be Bloch’s cycle complex of relative dimension
![]() $n$
considered in [Reference GeisserGei10]. It is the bounded above complex of sheaves on the small étale site of
$n$
considered in [Reference GeisserGei10]. It is the bounded above complex of sheaves on the small étale site of
![]() $X$
such that for any étale
$X$
such that for any étale
![]() $W\rightarrow X$
we have
$W\rightarrow X$
we have
Here
![]() $z_{q}(W,p)$
is the free abelian group generated by integral
$z_{q}(W,p)$
is the free abelian group generated by integral
![]() $(p+q)$
-dimensional subschemes of
$(p+q)$
-dimensional subschemes of
![]() $\unicode[STIX]{x1D6E5}_{W}^{p}$
that intersect all faces properly. We list some properties of
$\unicode[STIX]{x1D6E5}_{W}^{p}$
that intersect all faces properly. We list some properties of
![]() $\unicode[STIX]{x2124}_{X}^{c}(n)$
.
$\unicode[STIX]{x2124}_{X}^{c}(n)$
.
Lemma 3.2. If
![]() $\dim B=0$
, there are natural quasi-isomorphisms
$\dim B=0$
, there are natural quasi-isomorphisms
If
![]() $\dim B=1$
, there is a natural quasi-isomorphism
$\dim B=1$
, there is a natural quasi-isomorphism
![]() $\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x1D53E}_{m}[1]$
.
$\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x1D53E}_{m}[1]$
.
Proof. If
![]() $B$
is a field, then
$B$
is a field, then
![]() $\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x2124}$
follows directly from the definition and
$\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x2124}$
follows directly from the definition and
![]() $\unicode[STIX]{x2124}_{B}^{c}(-1)\cong \unicode[STIX]{x1D53E}_{m}[-1]$
follows from [Reference BlochBlo86, Corollary 6.4]. If
$\unicode[STIX]{x2124}_{B}^{c}(-1)\cong \unicode[STIX]{x1D53E}_{m}[-1]$
follows from [Reference BlochBlo86, Corollary 6.4]. If
![]() $B$
is a regular curve over a field, then
$B$
is a regular curve over a field, then
![]() $\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x1D53E}_{m}[1]$
follows again from [Reference BlochBlo86, Corollary 6.4]. For the general one-dimensional case see [Reference LevineLev99, Lemma 11.2] or [Reference SchmidtSch07, Corollary 3.9].◻
$\unicode[STIX]{x2124}_{B}^{c}(0)\cong \unicode[STIX]{x1D53E}_{m}[1]$
follows again from [Reference BlochBlo86, Corollary 6.4]. For the general one-dimensional case see [Reference LevineLev99, Lemma 11.2] or [Reference SchmidtSch07, Corollary 3.9].◻
The definition of
![]() $\unicode[STIX]{x2124}_{X}^{c}(n)$
naturally extends to schemes which are filtered inverse limits of étale
$\unicode[STIX]{x2124}_{X}^{c}(n)$
naturally extends to schemes which are filtered inverse limits of étale
![]() $X$
-schemes (e.g., the strict henselization of
$X$
-schemes (e.g., the strict henselization of
![]() $X$
at a geometric point). We will call such schemes étale essentially of finite type. The dimension of
$X$
at a geometric point). We will call such schemes étale essentially of finite type. The dimension of
![]() $W=\varprojlim W_{i}$
is defined as the common dimension of the
$W=\varprojlim W_{i}$
is defined as the common dimension of the
![]() $W_{i}$
. We have
$W_{i}$
. We have
If
![]() $\dim B=1$
,
$\dim B=1$
,
![]() $K=k(B)$
and
$K=k(B)$
and
![]() $X\rightarrow B$
factors through
$X\rightarrow B$
factors through
![]() $\operatorname{Spec}K$
, then our definition of dimension implies
$\operatorname{Spec}K$
, then our definition of dimension implies
Convention 3.3. In the following, we assume that
![]() $\unicode[STIX]{x1D6FD}$
is a natural number such that
$\unicode[STIX]{x1D6FD}$
is a natural number such that
![]() $k(b)$
is imperfect at most for points
$k(b)$
is imperfect at most for points
![]() $b\in B$
with
$b\in B$
with
![]() $\text{char}\,k(b)\mid \unicode[STIX]{x1D6FD}$
.
$\text{char}\,k(b)\mid \unicode[STIX]{x1D6FD}$
.
If
![]() $B$
is the spectrum of the ring of integers of a number field or a
$B$
is the spectrum of the ring of integers of a number field or a
![]() $p$
-adic field, we can put
$p$
-adic field, we can put
![]() $\unicode[STIX]{x1D6FD}=1$
. If
$\unicode[STIX]{x1D6FD}=1$
. If
![]() $\text{char}(k(B))=p>0$
, we can put
$\text{char}(k(B))=p>0$
, we can put
![]() $\unicode[STIX]{x1D6FD}=p$
.
$\unicode[STIX]{x1D6FD}=p$
.
Theorem 3.4 (Localization).
Let
![]() $n\leqslant 0$
and
$n\leqslant 0$
and
![]() $i:Z{\hookrightarrow}X$
a closed embedding with open complement
$i:Z{\hookrightarrow}X$
a closed embedding with open complement
![]() $j:U\rightarrow X$
. Then there is a natural isomorphism
$j:U\rightarrow X$
. Then there is a natural isomorphism
in the derived category of sheaves on
![]() $Z_{\acute{e} t}$
. In particular, we have a distinguished triangle
$Z_{\acute{e} t}$
. In particular, we have a distinguished triangle
in the derived category of sheaves on
![]() $X_{\acute{e} t}$
.
$X_{\acute{e} t}$
.
Proof. [Reference GeisserGei10, Corollary 7.2a)] applies with the same proof after tensoring with
![]() $\unicode[STIX]{x2124}[{\textstyle \frac{1}{\unicode[STIX]{x1D6FD}}}]$
. ◻
$\unicode[STIX]{x2124}[{\textstyle \frac{1}{\unicode[STIX]{x1D6FD}}}]$
. ◻
Theorem 3.5 (Duality).
Let
![]() $f:X\rightarrow B$
be separated and of finite type and let
$f:X\rightarrow B$
be separated and of finite type and let
![]() $\mathscr{F}^{\bullet }$
be a bounded torsion complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded torsion complex of sheaves on
![]() $X_{\acute{e} t}$
. Then, for
$X_{\acute{e} t}$
. Then, for
![]() $n\leqslant 0$
, we have a natural isomorphism in the derived category of abelian groups
$n\leqslant 0$
, we have a natural isomorphism in the derived category of abelian groups
Proof. [Reference GeisserGei10, Corollary 4.7b), Theorem 7.3] shows that
for a single torsion sheaf
![]() $\mathscr{F}$
, if
$\mathscr{F}$
, if
![]() $B$
is the spectrum of a perfect field or of a Dedekind domain of characteristic zero with perfect residue fields. Without the perfectness assumption, the same proof shows the isomorphism for general
$B$
is the spectrum of a perfect field or of a Dedekind domain of characteristic zero with perfect residue fields. Without the perfectness assumption, the same proof shows the isomorphism for general
![]() $B$
after inverting
$B$
after inverting
![]() $\unicode[STIX]{x1D6FD}$
. Finally, this extends in a straightforward manner to the case of a bounded complex
$\unicode[STIX]{x1D6FD}$
. Finally, this extends in a straightforward manner to the case of a bounded complex
![]() $\mathscr{F}^{\bullet }$
.◻
$\mathscr{F}^{\bullet }$
.◻
Corollary 3.6 (Modified duality).
Assume that
![]() $B=\operatorname{Spec}\unicode[STIX]{x211D}$
in Theorem 3.5. Then, for
$B=\operatorname{Spec}\unicode[STIX]{x211D}$
in Theorem 3.5. Then, for
![]() $n\leqslant 0$
, we have a natural isomorphism in the derived category of abelian groups
$n\leqslant 0$
, we have a natural isomorphism in the derived category of abelian groups
Proof. Let
![]() $X_{\unicode[STIX]{x2102}}=X\times _{\unicode[STIX]{x211D}}\unicode[STIX]{x2102}$
. The isomorphism
$X_{\unicode[STIX]{x2102}}=X\times _{\unicode[STIX]{x211D}}\unicode[STIX]{x2102}$
. The isomorphism
of Theorem 3.5 for
![]() $n\leqslant 0$
is
$n\leqslant 0$
is
![]() $\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
-invariant (cf. the proof of [Reference GeisserGei10, Theorem 4.1)]). By [Reference GeisserGei10, Lemma 4.8] the complexes in (3.5) are bounded. Hence we can apply
$\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D})$
-invariant (cf. the proof of [Reference GeisserGei10, Theorem 4.1)]). By [Reference GeisserGei10, Lemma 4.8] the complexes in (3.5) are bounded. Hence we can apply
![]() $\hat{\unicode[STIX]{x210D}}(\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D}),-)$
to obtain the result.◻
$\hat{\unicode[STIX]{x210D}}(\operatorname{Gal}(\unicode[STIX]{x2102}|\unicode[STIX]{x211D}),-)$
to obtain the result.◻
Working with sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules, we obtain a dimension shift by one by the following lemma.
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules, we obtain a dimension shift by one by the following lemma.
Lemma 3.7. Let
![]() $\mathscr{F}^{\bullet }$
be a bounded complex of sheaves of
$\mathscr{F}^{\bullet }$
be a bounded complex of sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $X_{\acute{e} t}$
. Then we have a natural isomorphism in the derived category of abelian groups
$X_{\acute{e} t}$
. Then we have a natural isomorphism in the derived category of abelian groups
Proof. This is standard homological algebra and has nothing to do with algebraic cycle complexes in particular. The proof of [Reference GeisserGei10, Lemma 2.4] applies without change. ◻
Let
![]() $X$
be a regular scheme which is étale essentially of finite type over
$X$
be a regular scheme which is étale essentially of finite type over
![]() $B$
and equidimensional of dimension
$B$
and equidimensional of dimension
![]() $d$
. Let
$d$
. Let
![]() $m$
be a natural number invertible on
$m$
be a natural number invertible on
![]() $B$
. Then, for
$B$
. Then, for
![]() $\dim B=0$
, the étale cycle class map
$\dim B=0$
, the étale cycle class map
![]() $c_{X}$
is defined in [Reference GeisserGL01]. It is a natural homomorphism
$c_{X}$
is defined in [Reference GeisserGL01]. It is a natural homomorphism
of complexes of sheaves on
![]() $X_{\acute{e} t}$
. We recall the following.
$X_{\acute{e} t}$
. We recall the following.
Theorem 3.8 [Reference GeisserGL01, Theorem 1.5].
If
![]() $\dim B=0$
and
$\dim B=0$
and
![]() $X$
is regular, then
$X$
is regular, then
![]() $c_{X}$
is a quasi-isomorphism for
$c_{X}$
is a quasi-isomorphism for
![]() $n\leqslant d$
.
$n\leqslant d$
.
The construction of
![]() $c_{X}$
extends to the case
$c_{X}$
extends to the case
![]() $\dim B=1$
as explained in [Reference LevineLev99, §12.3]. If
$\dim B=1$
as explained in [Reference LevineLev99, §12.3]. If
![]() $X\rightarrow B$
factors through
$X\rightarrow B$
factors through
![]() $\operatorname{Spec}K$
,
$\operatorname{Spec}K$
,
![]() $K=k(B)$
, then the cycle class maps over
$K=k(B)$
, then the cycle class maps over
![]() $B$
and over
$B$
and over
![]() $K$
are compatible, i.e., the diagram
$K$
are compatible, i.e., the diagram

commutes (note that
![]() $X$
has dimension
$X$
has dimension
![]() $d-1$
as a scheme over
$d-1$
as a scheme over
![]() $K$
).
$K$
).
Theorem 3.9. Assume
![]() $\dim B=1$
and that
$\dim B=1$
and that
![]() $X$
is étale essentially of finite type over
$X$
is étale essentially of finite type over
![]() $B$
, regular connected and of dimension
$B$
, regular connected and of dimension
![]() $d$
. Let
$d$
. Let
![]() $m$
be a natural number invertible on
$m$
be a natural number invertible on
![]() $X$
. Then the cycle class map
$X$
. Then the cycle class map
is a quasi-isomorphism for
![]() $n\leqslant 0$
.
$n\leqslant 0$
.
Remark 3.10. One expects that
![]() $c_{X}$
is a quasi-isomorphism for
$c_{X}$
is a quasi-isomorphism for
![]() $n\leqslant d$
.
$n\leqslant d$
.
Proof of Theorem 3.9.
The proof follows [Reference LevineLev99, Theorem 12.5]. We can assume that
![]() $B$
is local and strictly henselian. Let
$B$
is local and strictly henselian. Let
![]() $Y$
be essentially of finite type over
$Y$
be essentially of finite type over
![]() $B$
,
$B$
,
![]() $i:Z\rightarrow Y$
be a regular closed subscheme and
$i:Z\rightarrow Y$
be a regular closed subscheme and
![]() $j:W\rightarrow Y$
its open complement. We have the following map of distinguished triangles of complexes of sheaves on
$j:W\rightarrow Y$
its open complement. We have the following map of distinguished triangles of complexes of sheaves on
![]() $Y_{\acute{e} t}$
.
$Y_{\acute{e} t}$
.
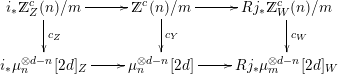
Indeed, the upper row is distinguished by Theorem 3.4, the lower row by purity of étale cohomology [Reference FujiwaraFuj00], and the commutativity of the diagram follows from the definition of the cycle class map, see [Reference LevineLev99, §12.3].
We see that if the result holds for two of
![]() $W,Z,Y$
, then it holds for the third. The special fibre of
$W,Z,Y$
, then it holds for the third. The special fibre of
![]() $Y$
has a finite stratification by closed subsets
$Y$
has a finite stratification by closed subsets
![]() $T_{i}$
such that
$T_{i}$
such that
![]() $T_{i}-T_{i+1}$
is regular. Thus the result follows by induction on
$T_{i}-T_{i+1}$
is regular. Thus the result follows by induction on
![]() $i$
from Theorem 3.8.◻
$i$
from Theorem 3.8.◻
The following lemma will be used in § 8.
Lemma 3.11. Let
![]() $\mathscr{F}$
be a locally constant, constructible sheaf of
$\mathscr{F}$
be a locally constant, constructible sheaf of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $X_{\acute{e} t}$
, where
$X_{\acute{e} t}$
, where
![]() $m$
is invertible on
$m$
is invertible on
![]() $X$
. Then, for
$X$
. Then, for
![]() $n\geqslant 0$
, we have natural isomorphisms in the derived category of abelian groups
$n\geqslant 0$
, we have natural isomorphisms in the derived category of abelian groups
Proof. We consider the local-to-global spectral sequence
By [Reference MilneMil80, III, Example 1.39(b)], we have for any
![]() $x\in X$
the isomorphisms of stalks
$x\in X$
the isomorphisms of stalks
Since
![]() $(\unicode[STIX]{x1D707}_{m}^{\otimes n})_{x}\cong \unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
is an injective
$(\unicode[STIX]{x1D707}_{m}^{\otimes n})_{x}\cong \unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
is an injective
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-module, we obtain
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-module, we obtain
Hence the spectral sequence degenerates showing the statement of the lemma. ◻
4 Arithmetic duality for complexes
Using the results of § 3, we generalize local and global duality theorems for single sheaves to bounded complexes and higher dimensions. For technical reasons, we also have to work with henselian local fields in the following sense.
Definition 4.1. In this paper a henselian local field is one of the following:
- (non-archimedean):
the quotient field of an excellent, henselian, discrete valuation ring with finite residue field;
- (complex):
an algebraically closed subfield of
 $\unicode[STIX]{x2102}$
;
$\unicode[STIX]{x2102}$
;- (real):
a relatively algebraically closed subfield of
 $\unicode[STIX]{x211D}$
.
$\unicode[STIX]{x211D}$
.
Remark 4.2. Complete discrete valuation rings are excellent by [Reference Grothendieck and DieudonnéEGA4, 7.8.3(iii)]. The local rings of global fields and their henselizations are excellent by [Reference Grothendieck and DieudonnéEGA4, 7.8.3 (ii)] and [Reference Grothendieck and DieudonnéEGA4, 18.7.6].
The henselian local fields of Definition 4.1 come with a natural valuation and their completions are the local fields in the usual sense. For a henselian local field
![]() $K$
with completion
$K$
with completion
![]() $\widehat{K}$
, the natural homomorphism of absolute Galois groups
$\widehat{K}$
, the natural homomorphism of absolute Galois groups
![]() $\text{Gal}_{\widehat{K}}\rightarrow \text{Gal}_{K}$
is an isomorphism by [Reference Artin, Grothendieck and VerdierSGA4, X, 2.2.1]. Hence the known statements about the Galois cohomology of local fields immediately extend to henselian local fields in the sense of Definition 4.1. Also the statement of Corollary 3.6 holds for arbitrary real henselian local fields.
$\text{Gal}_{\widehat{K}}\rightarrow \text{Gal}_{K}$
is an isomorphism by [Reference Artin, Grothendieck and VerdierSGA4, X, 2.2.1]. Hence the known statements about the Galois cohomology of local fields immediately extend to henselian local fields in the sense of Definition 4.1. Also the statement of Corollary 3.6 holds for arbitrary real henselian local fields.
Theorem 4.3 (Duality over henselian local fields).
Let
![]() $K$
be a henselian local field and let
$K$
be a henselian local field and let
![]() $f:X\rightarrow \operatorname{Spec}K$
be separated and of finite type. Let
$f:X\rightarrow \operatorname{Spec}K$
be separated and of finite type. Let
![]() $\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
![]() $X_{\acute{e} t}$
. If
$X_{\acute{e} t}$
. If
![]() $\text{char}(K)=p>0$
assume that
$\text{char}(K)=p>0$
assume that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p$
-torsion free. Then Tate’s local duality induces perfect pairings of finite abelian groups
$p$
-torsion free. Then Tate’s local duality induces perfect pairings of finite abelian groups
for all
![]() $r\in \unicode[STIX]{x2124}$
.
$r\in \unicode[STIX]{x2124}$
.
Proof. We start with the case
![]() $X=\operatorname{Spec}K$
and a single sheaf
$X=\operatorname{Spec}K$
and a single sheaf
![]() $\mathscr{F}$
. By Tate’s local duality theorem [Reference Neukirch, Schmidt and WingbergNSW08, (7.2.6), (7.2.17)], the cup product followed by the invariant map of local class field theory induce a perfect pairing of finite abelian groups
$\mathscr{F}$
. By Tate’s local duality theorem [Reference Neukirch, Schmidt and WingbergNSW08, (7.2.6), (7.2.17)], the cup product followed by the invariant map of local class field theory induce a perfect pairing of finite abelian groups
for all
![]() $r\in \unicode[STIX]{x2124}$
. Since
$r\in \unicode[STIX]{x2124}$
. Since
![]() ${\mathcal{H}}\!\mathit{om}_{K}(-,\unicode[STIX]{x1D53E}_{m})$
is exact on prime-to-
${\mathcal{H}}\!\mathit{om}_{K}(-,\unicode[STIX]{x1D53E}_{m})$
is exact on prime-to-
![]() $p$
torsion sheaves, we have
$p$
torsion sheaves, we have
![]() ${\mathcal{E}}\!xt_{K}^{i}(\mathscr{F},\unicode[STIX]{x1D53E}_{m})=0$
for
${\mathcal{E}}\!xt_{K}^{i}(\mathscr{F},\unicode[STIX]{x1D53E}_{m})=0$
for
![]() $i>0$
and the local to global spectral sequence implies that
$i>0$
and the local to global spectral sequence implies that
By Lemma 3.2, we have
![]() $\unicode[STIX]{x2124}_{K}^{c}(-1)\cong \unicode[STIX]{x1D53E}_{m}[-1]$
. This shows the perfect pairing of the theorem for a single sheaf and the result for a bounded complex
$\unicode[STIX]{x2124}_{K}^{c}(-1)\cong \unicode[STIX]{x1D53E}_{m}[-1]$
. This shows the perfect pairing of the theorem for a single sheaf and the result for a bounded complex
![]() $\mathscr{F}^{\bullet }$
follows from the map of hypercohomology spectral sequences as shown here.
$\mathscr{F}^{\bullet }$
follows from the map of hypercohomology spectral sequences as shown here.

In the general case, we have
by definition. Furthermore,
by Theorem 3.5 and Corollary 3.6. Hence we obtain the asserted natural perfect pairing from the following diagram.

◻
Theorem 4.4 (Henselian local duality).
Let
![]() $K$
be a non-archimedean henselian local field,
$K$
be a non-archimedean henselian local field,
![]() $B=\operatorname{Spec}{\mathcal{O}}_{K}$
,
$B=\operatorname{Spec}{\mathcal{O}}_{K}$
,
![]() $b\in B$
the closed point and
$b\in B$
the closed point and
![]() $f:\mathscr{X}\rightarrow B$
separated and of finite type. Let
$f:\mathscr{X}\rightarrow B$
separated and of finite type. Let
![]() $\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
![]() $\mathscr{X}_{\acute{e} t}$
. If
$\mathscr{X}_{\acute{e} t}$
. If
![]() $\text{char}(K)=p>0$
assume that
$\text{char}(K)=p>0$
assume that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p$
-torsion free. Then the local duality on
$p$
-torsion free. Then the local duality on
![]() $B$
induces perfect pairings of finite abelian groups
$B$
induces perfect pairings of finite abelian groups
for all
![]() $r\in \unicode[STIX]{x2124}$
.
$r\in \unicode[STIX]{x2124}$
.
Remark 4.5. The group
![]() $H_{\{b\}}^{r}(B,Rf_{!}\mathscr{F}^{\bullet })$
is the cohomology of
$H_{\{b\}}^{r}(B,Rf_{!}\mathscr{F}^{\bullet })$
is the cohomology of
![]() $\mathscr{X}$
with compact support in the closed fibre.
$\mathscr{X}$
with compact support in the closed fibre.
Proof of Theorem 4.4.
We start with the case
![]() $\mathscr{X}=B$
and a single sheaf
$\mathscr{X}=B$
and a single sheaf
![]() $\mathscr{F}$
. Then the local duality theorem [Reference MilneMil86, II, Theorem 1.8(b)] states that
$\mathscr{F}$
. Then the local duality theorem [Reference MilneMil86, II, Theorem 1.8(b)] states that
is a perfect pairing of finite abelian groups for all
![]() $r\in \unicode[STIX]{x2124}$
. By Lemma 3.2, we have
$r\in \unicode[STIX]{x2124}$
. By Lemma 3.2, we have
![]() $\unicode[STIX]{x2124}_{B}^{c}\cong \unicode[STIX]{x1D53E}_{m}[1]$
. This shows the perfect pairing of the theorem for a single sheaf and the result for a bounded complex
$\unicode[STIX]{x2124}_{B}^{c}\cong \unicode[STIX]{x1D53E}_{m}[1]$
. This shows the perfect pairing of the theorem for a single sheaf and the result for a bounded complex
![]() $\mathscr{F}^{\bullet }$
follows from the hypercohomology spectral sequence.
$\mathscr{F}^{\bullet }$
follows from the hypercohomology spectral sequence.
In the general case, we obtain the asserted perfect pairing from the following diagram.

◻
Next we recall the construction of the trace isomorphism (cf. [Reference ZinkZin78, 2.5.9], [Reference MazurMaz73, §2] or [Reference MilneMil86, II, 2.6]). For
![]() $\mathscr{F}=\unicode[STIX]{x1D53E}_{m}$
and
$\mathscr{F}=\unicode[STIX]{x1D53E}_{m}$
and
![]() $S=$
(all places), Lemma 2.7 and the fact that
$S=$
(all places), Lemma 2.7 and the fact that
![]() $H_{v}^{n+1}(\mathscr{T},\unicode[STIX]{x1D53E}_{m})\cong H^{n}(k_{(v)},\unicode[STIX]{x1D53E}_{m})$
for
$H_{v}^{n+1}(\mathscr{T},\unicode[STIX]{x1D53E}_{m})\cong H^{n}(k_{(v)},\unicode[STIX]{x1D53E}_{m})$
for
![]() $n\geqslant 1$
yield an exact sequence
$n\geqslant 1$
yield an exact sequence
Therefore the classical Hasse principle for the Brauer group [Reference Neukirch, Schmidt and WingbergNSW08, (8.1.17)] implies the existence of a natural trace isomorphism
Theorem 4.6 (Generalized Artin–Verdier duality).
Let
![]() $k$
be a global field and
$k$
be a global field and
![]() $\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
. Let
$\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
. Let
![]() $f:\mathscr{X}\rightarrow \mathscr{B}$
be a separated scheme of finite type and
$f:\mathscr{X}\rightarrow \mathscr{B}$
be a separated scheme of finite type and
![]() $\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves on
![]() $\mathscr{X}_{\acute{e} t}$
. If
$\mathscr{X}_{\acute{e} t}$
. If
![]() $\text{char}(k)=p>0$
assume that
$\text{char}(k)=p>0$
assume that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p$
-torsion free. Then Artin–Verdier duality induces perfect pairings of finite abelian groups
$p$
-torsion free. Then Artin–Verdier duality induces perfect pairings of finite abelian groups
for all
![]() $r\in \unicode[STIX]{x2124}$
.
$r\in \unicode[STIX]{x2124}$
.
Proof. If
![]() $\mathscr{X}=\mathscr{B}$
, we have
$\mathscr{X}=\mathscr{B}$
, we have
![]() $\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0)=\unicode[STIX]{x1D53E}_{m}[1]$
by Lemma 3.2. In this case, the result follows by the hypercohomology spectral sequence from the classical Artin–Verdier duality for a single constructible sheaf
$\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0)=\unicode[STIX]{x1D53E}_{m}[1]$
by Lemma 3.2. In this case, the result follows by the hypercohomology spectral sequence from the classical Artin–Verdier duality for a single constructible sheaf
![]() $\mathscr{F}$
, see [Reference ZinkZin78, Theorem 3.2.1], [Reference MazurMaz73] and [Reference MilneMil86, II, Theorem 3.1], respectively [Reference MilneMil86, II, Theorem 6.2] if
$\mathscr{F}$
, see [Reference ZinkZin78, Theorem 3.2.1], [Reference MazurMaz73] and [Reference MilneMil86, II, Theorem 3.1], respectively [Reference MilneMil86, II, Theorem 6.2] if
![]() $\text{char}(k)=p>0$
.
$\text{char}(k)=p>0$
.
The general case then follows from
by definition, from
by Theorem 3.5, and from the fact that
![]() $Rf_{!}\mathscr{F}^{\bullet }$
is a bounded, constructible complex [Reference DeligneSGA4½].◻
$Rf_{!}\mathscr{F}^{\bullet }$
is a bounded, constructible complex [Reference DeligneSGA4½].◻
5 A base change property
Proposition 5.1. Let
![]() $B$
be an integral, noetherian and regular scheme of Krull-dimension
$B$
be an integral, noetherian and regular scheme of Krull-dimension
![]() ${\leqslant}1$
, and let
${\leqslant}1$
, and let
![]() $\unicode[STIX]{x1D6FD}$
be a natural number as in Convention 3.3. Let
$\unicode[STIX]{x1D6FD}$
be a natural number as in Convention 3.3. Let
![]() $(B_{i})_{i\in I}$
be a filtered inverse system of étale
$(B_{i})_{i\in I}$
be a filtered inverse system of étale
![]() $B$
-schemes and
$B$
-schemes and
![]() $B_{\infty }=\varprojlim B_{i}$
. Let
$B_{\infty }=\varprojlim B_{i}$
. Let
![]() $f:\mathscr{X}\rightarrow B$
be separated and of finite type and let
$f:\mathscr{X}\rightarrow B$
be separated and of finite type and let
![]() $\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
![]() $\mathscr{X}_{\acute{e} t}$
. Consider the following fibre product diagram.
$\mathscr{X}_{\acute{e} t}$
. Consider the following fibre product diagram.
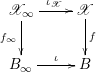
Then, for
![]() $n\leqslant 0$
, the natural map
$n\leqslant 0$
, the natural map
is an isomorphism in the derived category of sheaves on
![]() $(B_{\infty })_{\acute{e} t}$
.
$(B_{\infty })_{\acute{e} t}$
.
Proof. The natural map of the proposition is the composition of the following three maps: the first is the base change map of the fibre product diagram
The second is the map
induced by
![]() $\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(-,-)\rightarrow R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}_{\infty }}(\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }-,\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }-)$
, and the third is the map
$\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(-,-)\rightarrow R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}_{\infty }}(\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }-,\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }-)$
, and the third is the map
induced by the natural map
![]() $\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(n)\rightarrow \unicode[STIX]{x2124}_{\mathscr{X}_{\infty }}^{c}(n)$
. By Theorem 3.5, it suffices to show that the map
$\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(n)\rightarrow \unicode[STIX]{x2124}_{\mathscr{X}_{\infty }}^{c}(n)$
. By Theorem 3.5, it suffices to show that the map
is an isomorphism. By [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6],
![]() $Rf_{!}$
commutes with base change and sends bounded, constructible complexes to bounded, constructible complexes by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.3.6]. Hence we have
$Rf_{!}$
commutes with base change and sends bounded, constructible complexes to bounded, constructible complexes by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.3.6]. Hence we have
![]() $R{f_{\infty }}_{!}\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }\mathscr{F}^{\bullet }\cong \unicode[STIX]{x1D704}^{\ast }Rf_{!}\mathscr{F}^{\bullet }$
and it suffices to show that the map
$R{f_{\infty }}_{!}\unicode[STIX]{x1D704}_{\mathscr{X}}^{\ast }\mathscr{F}^{\bullet }\cong \unicode[STIX]{x1D704}^{\ast }Rf_{!}\mathscr{F}^{\bullet }$
and it suffices to show that the map
is an isomorphism for every bounded, constructible complex
![]() $\mathscr{F}^{\bullet }$
on
$\mathscr{F}^{\bullet }$
on
![]() $B$
. By the hypercohomology spectral sequence, we can assume that
$B$
. By the hypercohomology spectral sequence, we can assume that
![]() $\mathscr{F}^{\bullet }$
is a single sheaf
$\mathscr{F}^{\bullet }$
is a single sheaf
![]() $\mathscr{F}$
.
$\mathscr{F}$
.
A geometric point
![]() $\bar{x}\rightarrow B_{\infty }$
induces a compatible system of geometric points
$\bar{x}\rightarrow B_{\infty }$
induces a compatible system of geometric points
![]() $\bar{x}\rightarrow B_{i}\rightarrow B$
. Assume for the moment that
$\bar{x}\rightarrow B_{i}\rightarrow B$
. Assume for the moment that
![]() $\mathscr{F}$
is locally constant. Then by [Reference MilneMil80, III, Exercise 1.31 b)] and ??, the map induced by (5.1) on the stalks at
$\mathscr{F}$
is locally constant. Then by [Reference MilneMil80, III, Exercise 1.31 b)] and ??, the map induced by (5.1) on the stalks at
![]() $\bar{x}$
is the identity of
$\bar{x}$
is the identity of
This shows that (5.1) is an isomorphism if
![]() $\mathscr{F}$
is locally constant. For a general constructible
$\mathscr{F}$
is locally constant. For a general constructible
![]() $\mathscr{F}$
, there is a non-empty open
$\mathscr{F}$
, there is a non-empty open
![]() $j:U\rightarrow B$
such that
$j:U\rightarrow B$
such that
![]() $\mathscr{F}|_{U}$
is locally constant. Let
$\mathscr{F}|_{U}$
is locally constant. Let
![]() $i:Z\rightarrow B$
be the closed complement. Then
$i:Z\rightarrow B$
be the closed complement. Then
![]() $Z$
has dimension zero, hence
$Z$
has dimension zero, hence
![]() $i^{\ast }\mathscr{F}$
is locally constant. Using the short exact sequence
$i^{\ast }\mathscr{F}$
is locally constant. Using the short exact sequence
![]() $0\rightarrow j_{!}j^{\ast }\mathscr{F}\rightarrow \mathscr{F}\rightarrow i_{\ast }i^{\ast }\mathscr{F}\rightarrow 0$
, the results for
$0\rightarrow j_{!}j^{\ast }\mathscr{F}\rightarrow \mathscr{F}\rightarrow i_{\ast }i^{\ast }\mathscr{F}\rightarrow 0$
, the results for
![]() $j^{\ast }\mathscr{F}$
and
$j^{\ast }\mathscr{F}$
and
![]() $i^{\ast }\mathscr{F}$
, the adjunctions
$i^{\ast }\mathscr{F}$
, the adjunctions
![]() $i_{\ast }\dashv i^{!}$
,
$i_{\ast }\dashv i^{!}$
,
![]() $j_{!}\dashv j^{\ast }$
, and Theorem 3.4 imply the result for
$j_{!}\dashv j^{\ast }$
, and Theorem 3.4 imply the result for
![]() $\mathscr{F}$
.◻
$\mathscr{F}$
.◻
Remark 5.2. We will apply Proposition 5.1 in the following situations:
–
 $B_{\infty }=\operatorname{Spec}{\mathcal{O}}_{S}$
,
$B_{\infty }=\operatorname{Spec}{\mathcal{O}}_{S}$
,
 $S$
an infinite set of primes;
$S$
an infinite set of primes;–
 $B_{\infty }=\operatorname{Spec}{\mathcal{O}}_{(v)}$
, the henselization.
$B_{\infty }=\operatorname{Spec}{\mathcal{O}}_{(v)}$
, the henselization.
6 Some restricted products
We recall the notion of a restricted product of topological groups. Assume we are given a family
![]() $(A_{i})_{i\in I}$
of Hausdorff abelian groups and let an open subgroup
$(A_{i})_{i\in I}$
of Hausdorff abelian groups and let an open subgroup
![]() $B_{i}\subset A_{i}$
be given for almost all
$B_{i}\subset A_{i}$
be given for almost all
![]() $i$
. For consistency of notation, we put
$i$
. For consistency of notation, we put
![]() $B_{i}=A_{i}$
for the remaining indices. The restricted product
$B_{i}=A_{i}$
for the remaining indices. The restricted product
![]() $\prod _{i\in I}(A_{i},B_{i})$
is the subgroup of
$\prod _{i\in I}(A_{i},B_{i})$
is the subgroup of
![]() $\prod A_{i}$
consisting of all
$\prod A_{i}$
consisting of all
![]() $(x_{i})_{i\in I}$
such that
$(x_{i})_{i\in I}$
such that
![]() $x_{i}\in B_{i}$
for almost all
$x_{i}\in B_{i}$
for almost all
![]() $i$
. It becomes a topological group by defining the products
$i$
. It becomes a topological group by defining the products
![]() $\prod _{i\in J}U_{i}\times \prod _{i\in I\smallsetminus J}B_{i}$
, where
$\prod _{i\in J}U_{i}\times \prod _{i\in I\smallsetminus J}B_{i}$
, where
![]() $J$
runs through the finite subsets of
$J$
runs through the finite subsets of
![]() $I$
and
$I$
and
![]() $U_{i}$
runs through a basis of neighbourhoods of the identity of
$U_{i}$
runs through a basis of neighbourhoods of the identity of
![]() $A_{i}$
for
$A_{i}$
for
![]() $i\in J$
as a basis of neighbourhoods of the identity. Note that
$i\in J$
as a basis of neighbourhoods of the identity. Note that
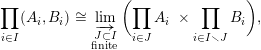 $$\begin{eqnarray}\mathop{\prod }_{i\in I}(A_{i},B_{i})\cong \mathop{\varinjlim }\nolimits_{\substack{ J\subset I \\ \text{finite }}}\biggl(\mathop{\prod }_{i\in J}A_{i}~\times \mathop{\prod }_{i\in I\smallsetminus J}B_{i}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i\in I}(A_{i},B_{i})\cong \mathop{\varinjlim }\nolimits_{\substack{ J\subset I \\ \text{finite }}}\biggl(\mathop{\prod }_{i\in J}A_{i}~\times \mathop{\prod }_{i\in I\smallsetminus J}B_{i}\biggr),\end{eqnarray}$$
both in the algebraic and the topological sense, i.e., the direct limit topology on the right-hand side is a group topology and coincides with the given topology on the left-hand side. Also note that the transition maps in the direct system are injective and open. In particular, for finite
![]() $J\subset I$
, the groups
$J\subset I$
, the groups
![]() $\prod _{i\in J}A_{i}~\times \prod _{i\in I\smallsetminus J}B_{i}$
are open subgroups of the restricted product.
$\prod _{i\in J}A_{i}~\times \prod _{i\in I\smallsetminus J}B_{i}$
are open subgroups of the restricted product.
Let
![]() $k$
be a global field,
$k$
be a global field,
![]() $X/k$
separated and of finite type,
$X/k$
separated and of finite type,
![]() $m\geqslant 1$
an integer prime to
$m\geqslant 1$
an integer prime to
![]() $p=\text{char}(k)$
and
$p=\text{char}(k)$
and
![]() $\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves of
$\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $X_{\acute{e} t}$
. We choose a separated scheme of finite type
$X_{\acute{e} t}$
. We choose a separated scheme of finite type
![]() $f:\mathscr{X}\rightarrow \mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
extending
$f:\mathscr{X}\rightarrow \mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
extending
![]() $X$
, i.e.,
$X$
, i.e.,
![]() $X=\mathscr{X}\times _{\mathscr{B}}k$
. Choosing
$X=\mathscr{X}\times _{\mathscr{B}}k$
. Choosing
![]() $\mathscr{X}$
small enough, we can assume that
$\mathscr{X}$
small enough, we can assume that
![]() $\mathscr{F}^{\bullet }$
is the restriction of a bounded, constructible complex of sheaves of
$\mathscr{F}^{\bullet }$
is the restriction of a bounded, constructible complex of sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{X}_{\acute{e} t}$
to
$\mathscr{X}_{\acute{e} t}$
to
![]() $X_{\acute{e} t}$
. By abuse of notation, we will denote this complex also by
$X_{\acute{e} t}$
. By abuse of notation, we will denote this complex also by
![]() $\mathscr{F}^{\bullet }$
. For non-archimedean
$\mathscr{F}^{\bullet }$
. For non-archimedean
![]() $v$
, we define the unramified part
$v$
, we define the unramified part
as the image of the restriction map
 $$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{\mathscr{X}_{(v)}}^{n-2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \operatorname{Ext}_{X_{(v)}}^{n-2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}/\mathscr{B}_{v}}^{c}(0))\stackrel{\text{Eq.}\,(3.3)}{=}\operatorname{Ext}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{Ext}_{\mathscr{X}_{(v)}}^{n-2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \operatorname{Ext}_{X_{(v)}}^{n-2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}/\mathscr{B}_{v}}^{c}(0))\stackrel{\text{Eq.}\,(3.3)}{=}\operatorname{Ext}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1)).\end{eqnarray}$$
Definition 6.1. For a set of primes
![]() $S$
we let
$S$
we let
be the restricted product with respect to the unramified parts (defined for non-archimedean
![]() $v$
). We equip the factors
$v$
). We equip the factors
![]() $\widehat{\operatorname{Ext}}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
with the discrete topology and
$\widehat{\operatorname{Ext}}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
with the discrete topology and
![]() $Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
with the restricted product topology.
$Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
with the restricted product topology.
Lemma 6.2.
(i)
 $Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
is independent of the choice of
$Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
is independent of the choice of
 $\mathscr{X}$
.
$\mathscr{X}$
.(ii)
 $Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
is a locally compact topological group.
$Q_{S}^{n}(X,\mathscr{F}^{\bullet })$
is a locally compact topological group.
Proof. (i) If
![]() $\mathscr{X}_{1}$
and
$\mathscr{X}_{1}$
and
![]() $\mathscr{X}_{2}$
are separated schemes of finite type over
$\mathscr{X}_{2}$
are separated schemes of finite type over
![]() $\mathscr{B}$
with generic fibre
$\mathscr{B}$
with generic fibre
![]() $X$
, then there exists a non-empty open subscheme
$X$
, then there exists a non-empty open subscheme
![]() $\mathscr{U}\subset \mathscr{B}$
and an isomorphism
$\mathscr{U}\subset \mathscr{B}$
and an isomorphism
![]() $\mathscr{X}_{1}|_{\mathscr{U}}\stackrel{{\sim}}{\longrightarrow }\mathscr{X}_{2}|_{\mathscr{U}}$
extending the identity of
$\mathscr{X}_{1}|_{\mathscr{U}}\stackrel{{\sim}}{\longrightarrow }\mathscr{X}_{2}|_{\mathscr{U}}$
extending the identity of
![]() $X$
. Shrinking
$X$
. Shrinking
![]() $\mathscr{U}$
once more, we may assume that this isomorphism identifies the chosen extensions of the constructible complex
$\mathscr{U}$
once more, we may assume that this isomorphism identifies the chosen extensions of the constructible complex
![]() $\mathscr{F}^{\bullet }$
. Hence the subgroups
$\mathscr{F}^{\bullet }$
. Hence the subgroups
![]() $\operatorname{Ext}_{X_{(v)},\mathit{nr}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
defined with respect to
$\operatorname{Ext}_{X_{(v)},\mathit{nr}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
defined with respect to
![]() $\mathscr{X}_{1}$
and
$\mathscr{X}_{1}$
and
![]() $\mathscr{X}_{2}$
coincide for all
$\mathscr{X}_{2}$
coincide for all
![]() $v\in \mathscr{U}$
, i.e., for almost all
$v\in \mathscr{U}$
, i.e., for almost all
![]() $v$
, and the restricted products are the same.
$v$
, and the restricted products are the same.
(ii) The factors
![]() $\widehat{\operatorname{Ext}}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
are finite by Theorem 4.4, hence compact with the discrete topology. Therefore the restricted product is locally compact by [Reference Neukirch, Schmidt and WingbergNSW08, (1.1.13)].◻
$\widehat{\operatorname{Ext}}_{X_{(v)}}^{n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))$
are finite by Theorem 4.4, hence compact with the discrete topology. Therefore the restricted product is locally compact by [Reference Neukirch, Schmidt and WingbergNSW08, (1.1.13)].◻
We recall the following lemma due to Saito.
Lemma 6.3. Let
![]() ${\mathcal{O}}$
be a henselian, discrete valuation ring with quotient field
${\mathcal{O}}$
be a henselian, discrete valuation ring with quotient field
![]() $K$
,
$K$
,
![]() $m\geqslant 1$
an integer prime to the residue characteristic of
$m\geqslant 1$
an integer prime to the residue characteristic of
![]() ${\mathcal{O}}$
and
${\mathcal{O}}$
and
![]() $\mathscr{F}^{\bullet }$
a bounded, locally constant, constructible complex of étale sheaves of
$\mathscr{F}^{\bullet }$
a bounded, locally constant, constructible complex of étale sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\operatorname{Spec}{\mathcal{O}}$
. Then the natural map
$\operatorname{Spec}{\mathcal{O}}$
. Then the natural map
is injective for all
![]() $n$
.
$n$
.
Proof. See [Reference SaitoSai89, Lemma 1.3]. ◻
Lemma 6.4. For almost all non-archimedean places
![]() $v$
, the restriction maps
$v$
, the restriction maps
are injective.
Proof. By [Reference DeligneSGA4½, Theorem 1.1], there is a non-empty open subscheme
![]() $\mathscr{W}\subset \mathscr{B}$
such that
$\mathscr{W}\subset \mathscr{B}$
such that
![]() $m$
is invertible on
$m$
is invertible on
![]() $\mathscr{W}$
and the restriction of
$\mathscr{W}$
and the restriction of
![]() $Rf_{\ast }\mathscr{F}^{\bullet }$
to
$Rf_{\ast }\mathscr{F}^{\bullet }$
to
![]() $\mathscr{W}$
is locally constant, constructible. Let
$\mathscr{W}$
is locally constant, constructible. Let
![]() $\unicode[STIX]{x1D704}_{v}:\operatorname{Spec}{\mathcal{O}}_{(v)}\rightarrow \mathscr{B}$
be the natural morphism. Then the assumptions of Lemma 6.3 are satisfied for
$\unicode[STIX]{x1D704}_{v}:\operatorname{Spec}{\mathcal{O}}_{(v)}\rightarrow \mathscr{B}$
be the natural morphism. Then the assumptions of Lemma 6.3 are satisfied for
![]() $\unicode[STIX]{x1D704}_{v}^{\ast }Rf_{\ast }\mathscr{F}^{\bullet }$
showing that
$\unicode[STIX]{x1D704}_{v}^{\ast }Rf_{\ast }\mathscr{F}^{\bullet }$
showing that
is injective for all
![]() $v\in \mathscr{W}$
. Consider the following fibre product diagram.
$v\in \mathscr{W}$
. Consider the following fibre product diagram.

Since étale cohomology commutes with inverse limits of quasi-compact, quasi-separated schemes and affine transition maps [Reference Artin, Grothendieck and VerdierSGA4, VII, 5.8], we obtain an isomorphism
Hence the injectivity of (6.7) implies the injectivity of (6.4) for
![]() $v\in \mathscr{W}$
.
$v\in \mathscr{W}$
.
The injectivity of (6.5) follows by choosing a compactification
![]() $j:\mathscr{X}_{(v)}{\hookrightarrow}\overline{\mathscr{X}_{(v)}}$
and applying (6.4) to
$j:\mathscr{X}_{(v)}{\hookrightarrow}\overline{\mathscr{X}_{(v)}}$
and applying (6.4) to
![]() $j_{!}\mathscr{F}^{\bullet }$
.
$j_{!}\mathscr{F}^{\bullet }$
.
To show the injectivity of (6.6), we first show that
![]() $Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is bounded and constructible on a non-empty open subscheme
$Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is bounded and constructible on a non-empty open subscheme
![]() $\mathscr{W}\subset \mathscr{B}$
. Using Theorem 3.5, Lemma 3.7 and 3.2, we obtain
$\mathscr{W}\subset \mathscr{B}$
. Using Theorem 3.5, Lemma 3.7 and 3.2, we obtain
 $$\begin{eqnarray}\displaystyle Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0)) & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0))\nonumber\\ \displaystyle & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0)/m[-1])\nonumber\\ \displaystyle & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x1D707}_{m}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0)) & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0))\nonumber\\ \displaystyle & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{B}}^{c}(0)/m[-1])\nonumber\\ \displaystyle & \cong & \displaystyle R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x1D707}_{m}).\nonumber\end{eqnarray}$$
By [Reference Artin, Grothendieck and VerdierSGA4, XVII, Theorem 5.3.6],
![]() $Rf_{!}\mathscr{F}^{\bullet }$
is bounded and constructible on
$Rf_{!}\mathscr{F}^{\bullet }$
is bounded and constructible on
![]() $\mathscr{B}$
. By [Reference DeligneSGA4½, Corollary 1.6], it follows that
$\mathscr{B}$
. By [Reference DeligneSGA4½, Corollary 1.6], it follows that
![]() $R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x1D707}_{m})$
is bounded and constructible on
$R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{B},\,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(Rf_{!}\mathscr{F}^{\bullet },\unicode[STIX]{x1D707}_{m})$
is bounded and constructible on
![]() $\mathscr{B}[1/m]$
. We conclude that
$\mathscr{B}[1/m]$
. We conclude that
![]() $Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is locally constant, constructible on a non-empty open subscheme
$Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is locally constant, constructible on a non-empty open subscheme
![]() $\mathscr{W}\subset \mathscr{B}[1/m]$
. Applying Lemma 6.3 to
$\mathscr{W}\subset \mathscr{B}[1/m]$
. Applying Lemma 6.3 to
![]() $\unicode[STIX]{x1D704}_{v}^{\ast }Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
, we see that
$\unicode[STIX]{x1D704}_{v}^{\ast }Rf_{\ast }R\,{\mathcal{H}}\!\mathit{om}_{\mathscr{X}}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
, we see that
is injective for all
![]() $v\in \mathscr{W}$
. By Proposition 5.1, we obtain an isomorphism
$v\in \mathscr{W}$
. By Proposition 5.1, we obtain an isomorphism
Hence for
![]() $v\in \mathscr{W}$
, (6.9) can be written as the injection
$v\in \mathscr{W}$
, (6.9) can be written as the injection
This finishes the proof. ◻
For a set of places
![]() $S$
and a finite subset
$S$
and a finite subset
![]() $T\subset S$
we set
$T\subset S$
we set
Corollary 6.5. If we endow
![]() $M_{T}^{n}(X,S,\mathscr{F}^{\bullet })$
with the (compact) product topology, then there is a natural topological isomorphism
$M_{T}^{n}(X,S,\mathscr{F}^{\bullet })$
with the (compact) product topology, then there is a natural topological isomorphism
Proof. This follows directly from Lemma 6.4 and the definition of the topology of the restricted product. ◻
Definition 6.6. For non-archimedean
![]() $v$
we define the unramified part
$v$
we define the unramified part
as the image of the restriction map
![]() $H_{\acute{e} t}^{n}(\mathscr{X}_{(v)},\mathscr{F}^{\bullet })\rightarrow H_{\acute{e} t}^{n}(X_{(v)},\mathscr{F}^{\bullet })$
and define
$H_{\acute{e} t}^{n}(\mathscr{X}_{(v)},\mathscr{F}^{\bullet })\rightarrow H_{\acute{e} t}^{n}(X_{(v)},\mathscr{F}^{\bullet })$
and define
as the restricted product with respect to the unramified subgroup (defined for non-archimedean
![]() $v$
).We define
$v$
).We define
![]() $P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
in exactly the same way but using modified cohomology with compact support everywhere.
$P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
in exactly the same way but using modified cohomology with compact support everywhere.
Again
![]() $P_{S}^{n}(X,\mathscr{F}^{\bullet })$
and
$P_{S}^{n}(X,\mathscr{F}^{\bullet })$
and
![]() $P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
only depend on
$P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
only depend on
![]() $X$
and not of the choice of
$X$
and not of the choice of
![]() $\mathscr{X}$
. They are locally compact abelian groups and Lemma 6.4 shows the following.
$\mathscr{X}$
. They are locally compact abelian groups and Lemma 6.4 shows the following.
Corollary 6.7. There are natural topological isomorphisms
Finally, we observe
Proposition 6.8. The groups
![]() $P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
and
$P_{S,c}^{n}(X,\mathscr{F}^{\bullet })$
and
![]() $Q_{S}^{3-n}(X,\mathscr{F}^{\bullet })$
are Pontryagin dual to each other.
$Q_{S}^{3-n}(X,\mathscr{F}^{\bullet })$
are Pontryagin dual to each other.
Proof. By Theorem 4.3, we have for all
![]() $v\in S$
a perfect pairing of finite groups
$v\in S$
a perfect pairing of finite groups
It therefore suffices to show that for almost all
![]() $v\in S$
the respective unramified subgroups are their exact annihilators in (6.18). First of all, they annihilate each other because the pairing (6.18) restricted to the subgroups
$v\in S$
the respective unramified subgroups are their exact annihilators in (6.18). First of all, they annihilate each other because the pairing (6.18) restricted to the subgroups
![]() $H_{c}^{n}(\mathscr{X}_{(v)},\mathscr{F}^{\bullet })$
and
$H_{c}^{n}(\mathscr{X}_{(v)},\mathscr{F}^{\bullet })$
and
![]() $\operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))$
factors through
$\operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))$
factors through
![]() $\operatorname{Br}({\mathcal{O}}_{(v)})=0$
.
$\operatorname{Br}({\mathcal{O}}_{(v)})=0$
.
On the other hand,
![]() $Rf_{!}\mathscr{F}^{\bullet }$
is bounded and constructible on
$Rf_{!}\mathscr{F}^{\bullet }$
is bounded and constructible on
![]() $\mathscr{B}$
by [Reference Artin, Grothendieck and VerdierSGA4, XVII, Theorem 5.3.6]. Hence for almost all
$\mathscr{B}$
by [Reference Artin, Grothendieck and VerdierSGA4, XVII, Theorem 5.3.6]. Hence for almost all
![]() $v\in S$
the assumptions of Lemma 6.3 are satisfied and the long exact sequence with support for
$v\in S$
the assumptions of Lemma 6.3 are satisfied and the long exact sequence with support for
![]() $\operatorname{Spec}k_{(v)}\subset \operatorname{Spec}{\mathcal{O}}_{(v)}$
and
$\operatorname{Spec}k_{(v)}\subset \operatorname{Spec}{\mathcal{O}}_{(v)}$
and
![]() $Rf_{!}\mathscr{F}^{\bullet }$
splits into short exact sequences
$Rf_{!}\mathscr{F}^{\bullet }$
splits into short exact sequences
Now we observe that
and that
![]() $H_{v}^{n+1}({\mathcal{O}}_{(v)},Rf_{!}\mathscr{F}^{\bullet })\cong \operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))^{\vee }$
by Theorem 4.4. We obtain
$H_{v}^{n+1}({\mathcal{O}}_{(v)},Rf_{!}\mathscr{F}^{\bullet })\cong \operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))^{\vee }$
by Theorem 4.4. We obtain
and this equality of orders shows that the groups are their exact annihilators. ◻
7 The main results
Theorem 7.1. Let
![]() $S\supset S_{\infty }$
be a (not necessarily finite) set of places of the global field
$S\supset S_{\infty }$
be a (not necessarily finite) set of places of the global field
![]() $k$
and let
$k$
and let
![]() $\mathscr{X}_{\mathscr{S}}\rightarrow \mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
be a separated scheme of finite type. Let
$\mathscr{X}_{\mathscr{S}}\rightarrow \mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
be a separated scheme of finite type. Let
![]() $m\geqslant 1$
be an integer prime to
$m\geqslant 1$
be an integer prime to
![]() $p=\text{char}\,k$
and let
$p=\text{char}\,k$
and let
![]() $\mathscr{F}^{\bullet }$
be a bounded complex of constructible sheaves of
$\mathscr{F}^{\bullet }$
be a bounded complex of constructible sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
.
$(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
.
Then there is a natural long exact sequence of topological groups and strict homomorphisms
The groups
![]() $\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{\mathscr{S}}}^{c}(0))$
are discrete, the groups
$\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{\mathscr{S}}}^{c}(0))$
are discrete, the groups
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
![]() $H_{c}^{-n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
are compact for all
$H_{c}^{-n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
are compact for all
![]() $n\in \unicode[STIX]{x2124}$
. Furthermore, the maps
$n\in \unicode[STIX]{x2124}$
. Furthermore, the maps
![]() $\unicode[STIX]{x1D706}_{n}$
are proper and have finite kernel for all
$\unicode[STIX]{x1D706}_{n}$
are proper and have finite kernel for all
![]() $n\in \unicode[STIX]{x2124}$
.
$n\in \unicode[STIX]{x2124}$
.
Proof. We choose a separated scheme of finite type
![]() $f:\mathscr{X}\rightarrow \mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
extending
$f:\mathscr{X}\rightarrow \mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
extending
![]() $\mathscr{X}_{\mathscr{S}}$
, i.e., such that
$\mathscr{X}_{\mathscr{S}}$
, i.e., such that
![]() $\mathscr{X}_{\mathscr{S}}=\mathscr{X}\times _{\mathscr{B}}\mathscr{S}$
. Choosing
$\mathscr{X}_{\mathscr{S}}=\mathscr{X}\times _{\mathscr{B}}\mathscr{S}$
. Choosing
![]() $\mathscr{X}$
small enough, we can assume that
$\mathscr{X}$
small enough, we can assume that
![]() $\mathscr{F}^{\bullet }$
is the restriction of a bounded constructible complex of sheaves of
$\mathscr{F}^{\bullet }$
is the restriction of a bounded constructible complex of sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{X}_{\acute{e} t}$
to
$\mathscr{X}_{\acute{e} t}$
to
![]() $(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
. We will denote this complex also by
$(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
. We will denote this complex also by
![]() $\mathscr{F}^{\bullet }$
. We denote the common generic fibre of
$\mathscr{F}^{\bullet }$
. We denote the common generic fibre of
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{X}_{\mathscr{S}}$
by
$\mathscr{X}_{\mathscr{S}}$
by
![]() $X_{k}$
.
$X_{k}$
.
In the following, the letter
![]() $T$
will always denote a finite subset
$T$
will always denote a finite subset
![]() $T\subset S$
containing all archimedean places and all places
$T\subset S$
containing all archimedean places and all places
![]() $v$
for which the assertion of Lemma 6.4 fails. By
$v$
for which the assertion of Lemma 6.4 fails. By
![]() $j:\mathscr{T}\rightarrow \mathscr{B}$
we denote the open immersion.
$j:\mathscr{T}\rightarrow \mathscr{B}$
we denote the open immersion.
We apply Lemma 2.7 to the complex
![]() $Rf_{!}\mathscr{F}^{\bullet }|_{\mathscr{T}}=j^{\ast }Rf_{!}\mathscr{F}^{\bullet }$
on
$Rf_{!}\mathscr{F}^{\bullet }|_{\mathscr{T}}=j^{\ast }Rf_{!}\mathscr{F}^{\bullet }$
on
![]() $\mathscr{T}_{\acute{e} t}$
and obtain a long exact sequence
$\mathscr{T}_{\acute{e} t}$
and obtain a long exact sequence
We consider the terms in (7.1). We have
by Theorem 4.6. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \cong \bigoplus _{v\in T}\widehat{\operatorname{Ext}}_{X_{(v)}}^{3-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))^{\vee }\oplus \bigoplus _{v\in S\smallsetminus T}\operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))^{\vee }\nonumber\\ \displaystyle & & \displaystyle \qquad =M_{T}^{3-n}(X_{k},S,\mathscr{F}^{\bullet })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cong \bigoplus _{v\in T}\widehat{\operatorname{Ext}}_{X_{(v)}}^{3-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{(v)}}^{c}(-1))^{\vee }\oplus \bigoplus _{v\in S\smallsetminus T}\operatorname{Ext}_{\mathscr{X}_{(v)}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{(v)}}^{c}(0))^{\vee }\nonumber\\ \displaystyle & & \displaystyle \qquad =M_{T}^{3-n}(X_{k},S,\mathscr{F}^{\bullet })^{\vee }\end{eqnarray}$$
by Theorems 4.3 and 4.4. Finally, by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6] we have
where the cohomology group on the right-hand side is étale cohomology with compact support of
![]() $\mathscr{X}_{\mathscr{S}}$
as a scheme of finite type over
$\mathscr{X}_{\mathscr{S}}$
as a scheme of finite type over
![]() $\mathscr{S}$
. Hence we can write the dual sequence to (7.1) in the form
$\mathscr{S}$
. Hence we can write the dual sequence to (7.1) in the form
(we changed the index
![]() $n\mapsto -n$
in order to have a cohomological complex). This is a long exact sequence of compact abelian groups with continuous maps and the Ext-groups are finite. Passing to the direct limit over all finite
$n\mapsto -n$
in order to have a cohomological complex). This is a long exact sequence of compact abelian groups with continuous maps and the Ext-groups are finite. Passing to the direct limit over all finite
![]() $T\subset S$
, we obtain using Proposition 5.1 and Corollary 6.5 the long exact sequence
$T\subset S$
, we obtain using Proposition 5.1 and Corollary 6.5 the long exact sequence
The groups
![]() $\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{\mathscr{S}}}^{c}(0))$
are discrete, the groups
$\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}_{\mathscr{S}}}^{c}(0))$
are discrete, the groups
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
![]() $H_{c}^{-n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
are compact. Since all homomorphism in (7.6) are continuous, the same is true for the homomorphisms in (7.7).
$H_{c}^{-n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
are compact. Since all homomorphism in (7.6) are continuous, the same is true for the homomorphisms in (7.7).
Next we prove that all morphisms are strict. For this we have to show that for any two consecutive maps
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $\unicode[STIX]{x1D713}$
in the long exact sequence, the continuous bijection
$\unicode[STIX]{x1D713}$
in the long exact sequence, the continuous bijection
![]() $\text{im}(\unicode[STIX]{x1D719})\stackrel{{\sim}}{\rightarrow }\ker (\unicode[STIX]{x1D713})$
is a homeomorphism. Here
$\text{im}(\unicode[STIX]{x1D719})\stackrel{{\sim}}{\rightarrow }\ker (\unicode[STIX]{x1D713})$
is a homeomorphism. Here
![]() $\text{im}(\unicode[STIX]{x1D719})$
is equipped with the quotient topology and
$\text{im}(\unicode[STIX]{x1D719})$
is equipped with the quotient topology and
![]() $\ker (\unicode[STIX]{x1D713})$
with the subspace topology. The obvious case is
$\ker (\unicode[STIX]{x1D713})$
with the subspace topology. The obvious case is
Indeed, the group
![]() $\ker (\unicode[STIX]{x1D713})$
is discrete, hence
$\ker (\unicode[STIX]{x1D713})$
is discrete, hence
![]() $\text{im}(\unicode[STIX]{x1D719})\stackrel{{\sim}}{\rightarrow }\ker (\unicode[STIX]{x1D713})$
must be homeomorphic. Since
$\text{im}(\unicode[STIX]{x1D719})\stackrel{{\sim}}{\rightarrow }\ker (\unicode[STIX]{x1D713})$
must be homeomorphic. Since
![]() $H_{c}^{-n-1}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
is compact, we also obtain the assertion that
$H_{c}^{-n-1}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
is compact, we also obtain the assertion that
![]() $\ker (\unicode[STIX]{x1D713})=\ker (\unicode[STIX]{x1D706}_{n})$
is finite for all
$\ker (\unicode[STIX]{x1D713})=\ker (\unicode[STIX]{x1D706}_{n})$
is finite for all
![]() $n$
. Next we consider
$n$
. Next we consider
The image of
![]() $\unicode[STIX]{x1D719}$
is the union of the images of the maps
$\unicode[STIX]{x1D719}$
is the union of the images of the maps
By (7.6) and the finiteness of
![]() $\operatorname{Ext}_{\mathscr{X}_{\mathscr{T}}}^{n+2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
, each
$\operatorname{Ext}_{\mathscr{X}_{\mathscr{T}}}^{n+2}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
, each
![]() $\text{im}(\unicode[STIX]{x1D719}_{T})$
has finite index in
$\text{im}(\unicode[STIX]{x1D719}_{T})$
has finite index in
![]() $H_{c}^{-n}$
$H_{c}^{-n}$
![]() $(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
. Hence the images stabilize, i.e.,
$(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })^{\vee }$
. Hence the images stabilize, i.e.,
![]() $\text{im}(\unicode[STIX]{x1D719}_{T})=\text{im}(\unicode[STIX]{x1D719})$
for
$\text{im}(\unicode[STIX]{x1D719}_{T})=\text{im}(\unicode[STIX]{x1D719})$
for
![]() $T$
large enough. This shows that
$T$
large enough. This shows that
![]() $\text{im}(\unicode[STIX]{x1D719})$
is compact and thus homeomorphic to
$\text{im}(\unicode[STIX]{x1D719})$
is compact and thus homeomorphic to
![]() $\ker (\unicode[STIX]{x1D713})$
. Finally, we consider
$\ker (\unicode[STIX]{x1D713})$
. Finally, we consider
Here we have to show that the subgroup
![]() $\ker (\unicode[STIX]{x1D713})$
is discrete. For this it suffices to show that there is an open subgroup of
$\ker (\unicode[STIX]{x1D713})$
is discrete. For this it suffices to show that there is an open subgroup of
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
having finite intersection with
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
having finite intersection with
![]() $\ker (\unicode[STIX]{x1D713})$
. For sufficiently large finite
$\ker (\unicode[STIX]{x1D713})$
. For sufficiently large finite
![]() $T\subset S$
,
$T\subset S$
,
![]() $M_{T}(X_{k},S,\mathscr{F}^{\bullet })$
is a subgroup of
$M_{T}(X_{k},S,\mathscr{F}^{\bullet })$
is a subgroup of
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
. Since
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
. Since
![]() $\operatorname{Ext}_{\mathscr{X}_{\mathscr{T}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is finite, any such
$\operatorname{Ext}_{\mathscr{X}_{\mathscr{T}}}^{n+1}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))$
is finite, any such
![]() $M_{T}(X_{k},S,\mathscr{F}^{\bullet })$
has the required property.
$M_{T}(X_{k},S,\mathscr{F}^{\bullet })$
has the required property.
Finally, the properness of
![]() $\unicode[STIX]{x1D706}_{n}$
follows formally from what we already know: since
$\unicode[STIX]{x1D706}_{n}$
follows formally from what we already know: since
![]() $\ker (\unicode[STIX]{x1D706}_{n})$
is finite, it suffices to show that every compact subset of
$\ker (\unicode[STIX]{x1D706}_{n})$
is finite, it suffices to show that every compact subset of
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
has finite intersection with
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
has finite intersection with
![]() $\text{im}(\unicode[STIX]{x1D706}_{n})$
. But this is obvious since
$\text{im}(\unicode[STIX]{x1D706}_{n})$
. But this is obvious since
![]() $\text{im}(\unicode[STIX]{x1D706}_{n})$
is a discrete subgroup of
$\text{im}(\unicode[STIX]{x1D706}_{n})$
is a discrete subgroup of
![]() $Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
by the strictness of
$Q_{S}^{n+3}(X_{k},\mathscr{F}^{\bullet })$
by the strictness of
![]() $\unicode[STIX]{x1D706}_{n}$
.◻
$\unicode[STIX]{x1D706}_{n}$
.◻
Dualizing Theorem 7.1, we obtain the following result.
Theorem 7.2. Let
![]() $S\supset S_{\infty }$
be a (not necessarily finite) set of places of the global field
$S\supset S_{\infty }$
be a (not necessarily finite) set of places of the global field
![]() $k$
and let
$k$
and let
![]() $\mathscr{X}_{\mathscr{S}}\rightarrow \mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
be a separated scheme of finite type. Let
$\mathscr{X}_{\mathscr{S}}\rightarrow \mathscr{S}=\operatorname{Spec}{\mathcal{O}}_{S}$
be a separated scheme of finite type. Let
![]() $m\geqslant 1$
be an integer prime to
$m\geqslant 1$
be an integer prime to
![]() $p=\text{char}(k)>0$
and let
$p=\text{char}(k)>0$
and let
![]() $\mathscr{F}^{\bullet }$
be a bounded complex of constructible sheaves of
$\mathscr{F}^{\bullet }$
be a bounded complex of constructible sheaves of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
.
$(\mathscr{X}_{\mathscr{S}})_{\acute{e} t}$
.
Then there is a natural long exact sequence of topological groups and strict homomorphisms
The groups
![]() $H_{c}^{n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })$
are discrete, the groups
$H_{c}^{n}(\mathscr{X}_{\mathscr{S}},\mathscr{F}^{\bullet })$
are discrete, the groups
![]() $P_{S,c}^{n}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
$P_{S,c}^{n}(X_{k},\mathscr{F}^{\bullet })$
are locally compact, and the groups
![]() $\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))^{\vee }$
are compact for all
$\operatorname{Ext}_{\mathscr{X}_{\mathscr{S}}}^{1-n}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{\mathscr{X}}^{c}(0))^{\vee }$
are compact for all
![]() $n\in \unicode[STIX]{x2124}$
. Furthermore, the maps
$n\in \unicode[STIX]{x2124}$
. Furthermore, the maps
![]() $\unicode[STIX]{x1D706}_{n,c}$
are proper and have finite kernel for all
$\unicode[STIX]{x1D706}_{n,c}$
are proper and have finite kernel for all
![]() $n\in \unicode[STIX]{x2124}$
.
$n\in \unicode[STIX]{x2124}$
.
8 Proofs of Theorems A and B
Proof of Theorem B.
Now we assume that
![]() $\mathscr{X}_{\mathscr{S}}$
is regular and that
$\mathscr{X}_{\mathscr{S}}$
is regular and that
![]() $\mathscr{F}$
is a locally constant, constructible sheaf of
$\mathscr{F}$
is a locally constant, constructible sheaf of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules where
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules where
![]() $m$
is invertible on
$m$
is invertible on
![]() $\mathscr{S}$
. We will deduce Theorem B from Theorem 7.1. The scheme
$\mathscr{S}$
. We will deduce Theorem B from Theorem 7.1. The scheme
![]() $\mathscr{X}$
in Theorem B is
$\mathscr{X}$
in Theorem B is
![]() $\mathscr{X}_{\mathscr{S}}$
of Theorem 7.1 and the relative dimension
$\mathscr{X}_{\mathscr{S}}$
of Theorem 7.1 and the relative dimension
![]() $r$
occurring in Theorem B is
$r$
occurring in Theorem B is
![]() $d-1$
, where
$d-1$
, where
![]() $d=\dim \mathscr{X}_{\mathscr{S}}$
according to Definition 3.1. As before, we extend the situation to a scheme
$d=\dim \mathscr{X}_{\mathscr{S}}$
according to Definition 3.1. As before, we extend the situation to a scheme
![]() $\mathscr{X}$
of finite type over
$\mathscr{X}$
of finite type over
![]() $\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
.
$\mathscr{B}=\operatorname{Spec}{\mathcal{O}}_{\varnothing }$
.
Step 1. We have
and for any non-archimedean
![]() $v$
,
$v$
,
Proof of Step 1. We have
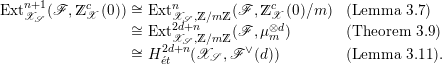
The proof of the second statement is similar.
Step 2. For
![]() $v\in S$
we have
$v\in S$
we have
Proof of Step 2. We have
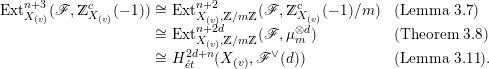
From Steps 1 and 2, we immediately obtain
Applying Theorem 7.1 to
![]() $\mathscr{F}^{\vee }(d)$
, we obtain the exact sequence of Theorem B except at the boundaries.
$\mathscr{F}^{\vee }(d)$
, we obtain the exact sequence of Theorem B except at the boundaries.
Step 3.
is injective and
is surjective.
Proof of Step 3. The injectivity of
![]() $\unicode[STIX]{x1D706}_{0}$
follows from our assumption that
$\unicode[STIX]{x1D706}_{0}$
follows from our assumption that
![]() $S$
contains at least one non-archimedean prime. The second map is dual to the injective map
$S$
contains at least one non-archimedean prime. The second map is dual to the injective map
hence surjective. This shows Theorem B (in the variant with henselizations instead of completions). For further use, we mention that for
![]() $i<0$
, our long exact sequence consists of isomorphisms
$i<0$
, our long exact sequence consists of isomorphisms
◻
Dualizing, one obtains a version with compact supports as follows.
Theorem C (Poitou–Tate exact sequence with compact support).
For
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $\mathscr{S}$
and
$\mathscr{S}$
and
![]() $\mathscr{F}$
as in Theorem A, we have an exact
$\mathscr{F}$
as in Theorem A, we have an exact
![]() $6r+9$
-term sequence of abelian topological groups and strict homomorphisms
$6r+9$
-term sequence of abelian topological groups and strict homomorphisms
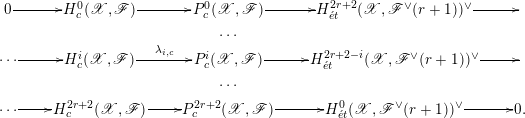
Here
is the restricted product with respect to the subgroups
![]() $H_{c,\mathit{nr}}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})$
. The localization maps
$H_{c,\mathit{nr}}^{i}(\mathscr{X}\otimes _{{\mathcal{O}}_{S}}k_{v},\mathscr{F})$
. The localization maps
![]() $\unicode[STIX]{x1D706}_{i}$
are proper and have finite kernel for all
$\unicode[STIX]{x1D706}_{i}$
are proper and have finite kernel for all
![]() $i$
, and for
$i$
, and for
![]() $i\geqslant 2r+3$
,
$i\geqslant 2r+3$
,
is an isomorphism. The groups in the left column of (8.2) are discrete, those in the middle column locally compact, and those in the right column compact.
Proof of Theorems A and C.
Applying Pontryagin duality to Theorem B, we obtain the sequence of Theorem C in view of
by Proposition 6.8. It remains to show the statement about
![]() $\unicode[STIX]{x1D706}_{i,c}$
. The isomorphism for
$\unicode[STIX]{x1D706}_{i,c}$
. The isomorphism for
![]() $i\geqslant 2r+3$
follows by dualizing from the last observation (8.1) in the proof of Theorem B. Furthermore, the topological exactness of the sequence shows
$i\geqslant 2r+3$
follows by dualizing from the last observation (8.1) in the proof of Theorem B. Furthermore, the topological exactness of the sequence shows
Hence the finiteness of
![]() $\ker (\unicode[STIX]{x1D706}_{i})$
for all
$\ker (\unicode[STIX]{x1D706}_{i})$
for all
![]() $i$
shows the finiteness of
$i$
shows the finiteness of
![]() $\ker (\unicode[STIX]{x1D706}_{i,c})$
for all
$\ker (\unicode[STIX]{x1D706}_{i,c})$
for all
![]() $i$
. Furthermore, (8.5) shows Theorem A since
$i$
. Furthermore, (8.5) shows Theorem A since
◻
9 Euler–Poincaré characteristic
To complete the picture, we calculate the Euler–Poincaré characteristic. We assume that the base field
![]() $k$
has no real embeddings so that
$k$
has no real embeddings so that
![]() $\mathscr{X}$
has finite cohomological dimension. We also assume that
$\mathscr{X}$
has finite cohomological dimension. We also assume that
![]() $S$
is finite, hence the cohomology with values in constructible coefficients is finite. Let
$S$
is finite, hence the cohomology with values in constructible coefficients is finite. Let
![]() $\mathscr{F}$
be a constructible sheaf on
$\mathscr{F}$
be a constructible sheaf on
![]() $\mathscr{X}_{\acute{e} t}$
. Then we call
$\mathscr{X}_{\acute{e} t}$
. Then we call
the Euler–Poincaré characteristic of
![]() $\mathscr{F}$
. Let
$\mathscr{F}$
. Let
![]() $k^{s}$
be a separable closure of
$k^{s}$
be a separable closure of
![]() $k$
. Then we call
$k$
. Then we call
the geometric Euler–Poincaré characteristic of
![]() $\mathscr{F}$
. We let
$\mathscr{F}$
. We let
![]() $r_{2}$
be the number of complex places of
$r_{2}$
be the number of complex places of
![]() $k$
, hence by our assumptions
$k$
, hence by our assumptions
Theorem 9.1. Under the above assumptions assume that
![]() $m\geqslant 1$
is an integer invertible on
$m\geqslant 1$
is an integer invertible on
![]() $\mathscr{S}$
and
$\mathscr{S}$
and
![]() $\mathscr{F}$
a locally constant, constructible sheaf of
$\mathscr{F}$
a locally constant, constructible sheaf of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{X}$
. Then we have
$\mathscr{X}$
. Then we have
In particular,
![]() $\unicode[STIX]{x1D712}(\mathscr{X},\mathscr{F})=1$
if
$\unicode[STIX]{x1D712}(\mathscr{X},\mathscr{F})=1$
if
![]() $\text{char}\,k>0$
.
$\text{char}\,k>0$
.
Proof. For a sheaf
![]() $\mathscr{G}$
of
$\mathscr{G}$
of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{S}$
, we have by [Reference MilneMil86, II, Theorem 2.13]
$\mathscr{S}$
, we have by [Reference MilneMil86, II, Theorem 2.13]
For a bounded, constructible complex
![]() $\mathscr{G}^{\bullet }$
of
$\mathscr{G}^{\bullet }$
of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules on
![]() $\mathscr{S}$
, we put
$\mathscr{S}$
, we put
Counting orders in the hypercohomology spectral sequence
![]() $E_{2}^{st}=H_{\acute{e} t}^{s}(\mathscr{S},H^{t}(\mathscr{G}^{\bullet }))\Rightarrow H_{\acute{e} t}^{s+t}(\mathscr{S},\mathscr{G}^{\bullet })$
, we obtain
$E_{2}^{st}=H_{\acute{e} t}^{s}(\mathscr{S},H^{t}(\mathscr{G}^{\bullet }))\Rightarrow H_{\acute{e} t}^{s+t}(\mathscr{S},\mathscr{G}^{\bullet })$
, we obtain
Any differential of the spectral sequence goes from a group with
![]() $s+t=i$
to a group with
$s+t=i$
to a group with
![]() $s+t=i+1$
. We therefore can replace the
$s+t=i+1$
. We therefore can replace the
![]() $E_{\infty }$
-terms in (9.6) by the
$E_{\infty }$
-terms in (9.6) by the
![]() $E_{2}$
-terms and obtain
$E_{2}$
-terms and obtain
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}\unicode[STIX]{x1D712}(\mathscr{S},\mathscr{G}^{\bullet })\ & =\ & \displaystyle \mathop{\prod }_{s,t}(\#E_{2}^{s,t})^{(-1)^{s+t}}=\displaystyle \mathop{\prod }_{t}\bigg(\mathop{\prod }_{s}(\#E_{2}^{s,t})^{(-1)^{s}}\bigg)^{(-1)^{t}}\\ \ & \stackrel{(9.1)}{=}\ & \displaystyle \mathop{\prod }_{t}\unicode[STIX]{x1D712}(\mathscr{S},H^{t}(\mathscr{G}^{\bullet }))\stackrel{(9.4)}{=}\displaystyle \mathop{\prod }_{i}(\#H^{i}(\mathscr{G}^{\bullet })(k^{s}))^{(-1)^{i+1}r_{2}}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\unicode[STIX]{x1D712}(\mathscr{S},\mathscr{G}^{\bullet })\ & =\ & \displaystyle \mathop{\prod }_{s,t}(\#E_{2}^{s,t})^{(-1)^{s+t}}=\displaystyle \mathop{\prod }_{t}\bigg(\mathop{\prod }_{s}(\#E_{2}^{s,t})^{(-1)^{s}}\bigg)^{(-1)^{t}}\\ \ & \stackrel{(9.1)}{=}\ & \displaystyle \mathop{\prod }_{t}\unicode[STIX]{x1D712}(\mathscr{S},H^{t}(\mathscr{G}^{\bullet }))\stackrel{(9.4)}{=}\displaystyle \mathop{\prod }_{i}(\#H^{i}(\mathscr{G}^{\bullet })(k^{s}))^{(-1)^{i+1}r_{2}}.\end{array}\end{eqnarray}$$
Applying this to
![]() $\mathscr{G}^{\bullet }=Rf_{\ast }\mathscr{F}$
, we obtain the result in view of
$\mathscr{G}^{\bullet }=Rf_{\ast }\mathscr{F}$
, we obtain the result in view of
![]() $H^{i}(Rf_{\ast }\mathscr{F})(k^{s})=H^{i}(X_{k^{s}},\mathscr{F}|_{X_{k^{s}}})$
.◻
$H^{i}(Rf_{\ast }\mathscr{F})(k^{s})=H^{i}(X_{k^{s}},\mathscr{F}|_{X_{k^{s}}})$
.◻
10 Henselization versus completion
The results of this section allow us to replace henselization by completion in Theorems 7.1 and 7.2. In particular, this shows Theorems A, B and C in the way they are formulated.
Proposition 10.1. Let
![]() $K$
be a henselian local field,
$K$
be a henselian local field,
![]() $f:X\rightarrow K$
separated and of finite type and
$f:X\rightarrow K$
separated and of finite type and
![]() $\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
a bounded, constructible complex of sheaves on
![]() $X_{\acute{e} t}$
. If
$X_{\acute{e} t}$
. If
![]() $\text{char}(K)=p>0$
assume that
$\text{char}(K)=p>0$
assume that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p$
-torsion free.
$p$
-torsion free.
Let
![]() $\widehat{K}$
be the completion of
$\widehat{K}$
be the completion of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D70B}_{X}$
the base change
$\unicode[STIX]{x1D70B}_{X}$
the base change
![]() $\unicode[STIX]{x1D70B}_{X}:X_{\widehat{K}}=X\times _{K}\widehat{K}\rightarrow X$
. Then the natural morphisms
$\unicode[STIX]{x1D70B}_{X}:X_{\widehat{K}}=X\times _{K}\widehat{K}\rightarrow X$
. Then the natural morphisms
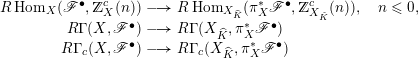 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}R\operatorname{Hom}_{X}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X}^{c}(n))\ & \longrightarrow \ & R\operatorname{Hom}_{X_{\widehat{K}}}(\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{\hat{K}}}^{c}(n)),\quad n\leqslant 0,\\ R\unicode[STIX]{x1D6E4}(X,\mathscr{F}^{\bullet })\ & \longrightarrow \ & R\unicode[STIX]{x1D6E4}(X_{\widehat{K}},\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet })\\ R\unicode[STIX]{x1D6E4}_{c}(X,\mathscr{F}^{\bullet })\ & \longrightarrow \ & R\unicode[STIX]{x1D6E4}_{c}(X_{\widehat{K}},\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet })\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}R\operatorname{Hom}_{X}(\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X}^{c}(n))\ & \longrightarrow \ & R\operatorname{Hom}_{X_{\widehat{K}}}(\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet },\unicode[STIX]{x2124}_{X_{\hat{K}}}^{c}(n)),\quad n\leqslant 0,\\ R\unicode[STIX]{x1D6E4}(X,\mathscr{F}^{\bullet })\ & \longrightarrow \ & R\unicode[STIX]{x1D6E4}(X_{\widehat{K}},\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet })\\ R\unicode[STIX]{x1D6E4}_{c}(X,\mathscr{F}^{\bullet })\ & \longrightarrow \ & R\unicode[STIX]{x1D6E4}_{c}(X_{\widehat{K}},\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}^{\bullet })\end{array}\end{eqnarray}$$
are isomorphisms in the derived category of abelian groups.
Proof. We start by proving the statements on
![]() $\text{R}\unicode[STIX]{x1D6E4}$
and
$\text{R}\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E4}_{c}$
. By [Reference Artin, Grothendieck and VerdierSGA4, X, 2.2.1],
$\unicode[STIX]{x1D6E4}_{c}$
. By [Reference Artin, Grothendieck and VerdierSGA4, X, 2.2.1],
![]() $K\rightarrow \hat{K}$
induces an isomorphism on absolute Galois groups. Hence we may replace
$K\rightarrow \hat{K}$
induces an isomorphism on absolute Galois groups. Hence we may replace
![]() $K$
and
$K$
and
![]() $\hat{K}$
by their separable closures and then the statement on
$\hat{K}$
by their separable closures and then the statement on
![]() $\text{R}\unicode[STIX]{x1D6E4}$
is a well known consequence of the smooth base change theorem, cf. [Reference MilneMil80, VI, 4.3]. Similarly, the statement on
$\text{R}\unicode[STIX]{x1D6E4}$
is a well known consequence of the smooth base change theorem, cf. [Reference MilneMil80, VI, 4.3]. Similarly, the statement on
![]() $R\unicode[STIX]{x1D6E4}_{c}$
follows since
$R\unicode[STIX]{x1D6E4}_{c}$
follows since
![]() $Rf_{!}$
commutes with base change by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6].
$Rf_{!}$
commutes with base change by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6].
Next we prove the assertion on
![]() $R\operatorname{Hom}$
. Using the hyperext spectral sequence, we can assume that
$R\operatorname{Hom}$
. Using the hyperext spectral sequence, we can assume that
![]() $\mathscr{F}^{\bullet }$
is a single constructible sheaf
$\mathscr{F}^{\bullet }$
is a single constructible sheaf
![]() $\mathscr{F}$
. If
$\mathscr{F}$
. If
![]() $i:Z\rightarrow X$
is a closed embedding with open complement
$i:Z\rightarrow X$
is a closed embedding with open complement
![]() $j:U\subset X$
, then we see by comparing the localization triangles associated with the short exact sequence
$j:U\subset X$
, then we see by comparing the localization triangles associated with the short exact sequence
![]() $j_{!}j^{\ast }\mathscr{F}\rightarrow \mathscr{F}\rightarrow i_{\ast }i^{\ast }\mathscr{F}$
,
$j_{!}j^{\ast }\mathscr{F}\rightarrow \mathscr{F}\rightarrow i_{\ast }i^{\ast }\mathscr{F}$
,
that the statements for two of
![]() $Z,U$
and
$Z,U$
and
![]() $X$
imply it for the third.
$X$
imply it for the third.
By induction on
![]() $d=\dim X$
, we may therefore assume that
$d=\dim X$
, we may therefore assume that
![]() $X$
is regular and connected, and
$X$
is regular and connected, and
![]() $\mathscr{F}$
is locally constant, constructible. Let
$\mathscr{F}$
is locally constant, constructible. Let
![]() $m\geqslant 1$
be an integer invertible in
$m\geqslant 1$
be an integer invertible in
![]() $K$
such that
$K$
such that
![]() $\mathscr{F}$
is a sheaf of
$\mathscr{F}$
is a sheaf of
![]() $\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules. Then we have
$\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}$
-modules. Then we have
 $$\begin{eqnarray}\begin{array}{@{}ccl@{}}R\operatorname{Hom}_{X}(\mathscr{F},\unicode[STIX]{x2124}_{X}^{c}(n))\ & \cong \ & R\operatorname{Hom}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x2124}_{X}^{c}(n)/m)[-1]\\ \ & \cong \ & R\operatorname{Hom}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x1D707}_{m}^{\otimes (d-n)})[2d-1]\\ \ & \cong \ & R\unicode[STIX]{x1D6E4}(X,{\mathcal{H}}\!\mathit{om}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x1D707}_{m}^{\otimes d-n}))[2d-1]\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccl@{}}R\operatorname{Hom}_{X}(\mathscr{F},\unicode[STIX]{x2124}_{X}^{c}(n))\ & \cong \ & R\operatorname{Hom}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x2124}_{X}^{c}(n)/m)[-1]\\ \ & \cong \ & R\operatorname{Hom}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x1D707}_{m}^{\otimes (d-n)})[2d-1]\\ \ & \cong \ & R\unicode[STIX]{x1D6E4}(X,{\mathcal{H}}\!\mathit{om}_{X,\unicode[STIX]{x2124}/m\unicode[STIX]{x2124}}(\mathscr{F},\unicode[STIX]{x1D707}_{m}^{\otimes d-n}))[2d-1]\end{array}\end{eqnarray}$$
by Lemma 3.7, Theorem 3.8, and Lemma 3.11. The same holds for
![]() $X_{\widehat{K}}$
and
$X_{\widehat{K}}$
and
![]() $\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}$
. Hence, by the first part of the proof, it suffices to show that
$\unicode[STIX]{x1D70B}_{X}^{\ast }\mathscr{F}$
. Hence, by the first part of the proof, it suffices to show that
is an isomorphism, which is clear since
![]() $\mathscr{F}$
is locally constant.◻
$\mathscr{F}$
is locally constant.◻
Proposition 10.2. Let
![]() $K$
be a non-archimedean henselian local field,
$K$
be a non-archimedean henselian local field,
![]() $B=\operatorname{Spec}{\mathcal{O}}_{K}$
and
$B=\operatorname{Spec}{\mathcal{O}}_{K}$
and
![]() $f:X\rightarrow B$
separated and of finite type. Let
$f:X\rightarrow B$
separated and of finite type. Let
![]() $\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
$\mathscr{F}^{\bullet }$
be a bounded, constructible complex of sheaves on
![]() $X_{\acute{e} t}$
. If
$X_{\acute{e} t}$
. If
![]() $\text{char}(K)=p>0$
assume that
$\text{char}(K)=p>0$
assume that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p$
-torsion free.
$p$
-torsion free.
Let
![]() $\widehat{K}$
be the completion of
$\widehat{K}$
be the completion of
![]() $K$
,
$K$
,
![]() $\widehat{B}=\operatorname{Spec}{\mathcal{O}}_{\widehat{K}}$
,
$\widehat{B}=\operatorname{Spec}{\mathcal{O}}_{\widehat{K}}$
,
![]() $\unicode[STIX]{x1D70B}:\widehat{B}\rightarrow B$
the projection and
$\unicode[STIX]{x1D70B}:\widehat{B}\rightarrow B$
the projection and
![]() $\unicode[STIX]{x1D70B}_{X}$
the base change
$\unicode[STIX]{x1D70B}_{X}$
the base change
![]() $\unicode[STIX]{x1D70B}_{X}:X_{\widehat{B}}=X\times _{B}\widehat{B}\rightarrow X$
. Then the natural morphisms
$\unicode[STIX]{x1D70B}_{X}:X_{\widehat{B}}=X\times _{B}\widehat{B}\rightarrow X$
. Then the natural morphisms
are isomorphisms in the derived category of abelian groups.
Assume in addition that
![]() $\mathscr{F}^{\bullet }$
is
$\mathscr{F}^{\bullet }$
is
![]() $p^{\prime }$
-torsion free, where
$p^{\prime }$
-torsion free, where
![]() $p^{\prime }$
is the residue characteristic of
$p^{\prime }$
is the residue characteristic of
![]() ${\mathcal{O}}_{K}$
. Then also
${\mathcal{O}}_{K}$
. Then also
is an isomorphism in the derived category of abelian groups.
Proof. As in the proof of Proposition 10.1, the statement for cohomology with compact support follows since
![]() $Rf_{!}$
commutes with base change by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6]. Since
$Rf_{!}$
commutes with base change by [Reference Artin, Grothendieck and VerdierSGA4, XVII, 5.2.6]. Since
![]() ${\mathcal{O}}_{K}$
is excellent by assumption, the ring homomorphism
${\mathcal{O}}_{K}$
is excellent by assumption, the ring homomorphism
![]() ${\mathcal{O}}_{K}\rightarrow {\mathcal{O}}_{\widehat{K}}$
is regular. Hence, by Popescu’s theorem [Sta17, Tag 07GB],
${\mathcal{O}}_{K}\rightarrow {\mathcal{O}}_{\widehat{K}}$
is regular. Hence, by Popescu’s theorem [Sta17, Tag 07GB],
![]() ${\mathcal{O}}_{\widehat{K}}$
, is the limit of smooth
${\mathcal{O}}_{\widehat{K}}$
, is the limit of smooth
![]() ${\mathcal{O}}_{K}$
-algebras. Therefore the statement on cohomology follows from the smooth base change theorem.
${\mathcal{O}}_{K}$
-algebras. Therefore the statement on cohomology follows from the smooth base change theorem.
Finally, we consider
![]() $R\operatorname{Hom}$
. Considering
$R\operatorname{Hom}$
. Considering
![]() $U\subset X$
open and
$U\subset X$
open and
![]() $Z=X\smallsetminus U$
, we see as in the proof of Proposition 10.1 that the statements for two of
$Z=X\smallsetminus U$
, we see as in the proof of Proposition 10.1 that the statements for two of
![]() $Z,U$
and
$Z,U$
and
![]() $X$
imply it for the third. As the closed fibres of
$X$
imply it for the third. As the closed fibres of
![]() $X$
and
$X$
and
![]() $X_{\hat{B}}$
coincide, it suffices to prove the statement for the generic fibre. Since
$X_{\hat{B}}$
coincide, it suffices to prove the statement for the generic fibre. Since
![]() $\unicode[STIX]{x2124}_{X/B}^{c}(n)|_{X_{K}}\cong \unicode[STIX]{x2124}_{X/K}^{c}(n-1)[2]$
, this follows from Proposition 10.1.◻
$\unicode[STIX]{x2124}_{X/B}^{c}(n)|_{X_{K}}\cong \unicode[STIX]{x2124}_{X/K}^{c}(n-1)[2]$
, this follows from Proposition 10.1.◻
Acknowledgement
The authors thank the anonymous referee for the thorough reading and constructive comments.




