Article contents
On the unramified spectrum of spherical varieties over p-adic fields
Published online by Cambridge University Press: 01 July 2008
Abstract
The description of irreducible representations of a group G can be seen as a problem in harmonic analysis; namely, decomposing a suitable space of functions on G into irreducibles for the action of G×G by left and right multiplication. For a split p-adic reductive group G over a local non-archimedean field, unramified irreducible smooth representations are in bijection with semisimple conjugacy classes in the ‘Langlands dual’ group. We generalize this description to an arbitrary spherical variety X of G as follows. Irreducible unramified quotients of the space 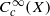 are in natural ‘almost bijection’ with a number of copies of AX*/WX, the quotient of a complex torus by the ‘little Weyl group’ of X. This leads to a description of the Hecke module of unramified vectors (a weak analog of geometric results of Gaitsgory and Nadler), and an understanding of the phenomenon that representations ‘distinguished’ by certain subgroups are functorial lifts. In the course of the proof, rationality properties of spherical varieties are examined and a new interpretation is given for the action, defined by Knop, of the Weyl group on the set of Borel orbits.
are in natural ‘almost bijection’ with a number of copies of AX*/WX, the quotient of a complex torus by the ‘little Weyl group’ of X. This leads to a description of the Hecke module of unramified vectors (a weak analog of geometric results of Gaitsgory and Nadler), and an understanding of the phenomenon that representations ‘distinguished’ by certain subgroups are functorial lifts. In the course of the proof, rationality properties of spherical varieties are examined and a new interpretation is given for the action, defined by Knop, of the Weyl group on the set of Borel orbits.
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2008
- 15
- Cited by




