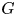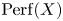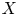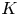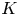1. Introduction
This paper is the first part of a project aimed at better understanding certain sophisticated ring-like structures that occur in ‘homotopical mathematics’. By this, we mean not just the theory of ![]() $E_{\infty }$-rings, where additions and multiplications are indexed over finite sets, but also more exotic structures occurring in equivariant and motivic homotopy theory where operations can be indexed over finite
$E_{\infty }$-rings, where additions and multiplications are indexed over finite sets, but also more exotic structures occurring in equivariant and motivic homotopy theory where operations can be indexed over finite ![]() $G$-sets and finite étale morphisms, respectively. Such structures are also relevant to derived algebraic geometry and algebraic
$G$-sets and finite étale morphisms, respectively. Such structures are also relevant to derived algebraic geometry and algebraic ![]() $K$-theory.
$K$-theory.
In the present paper we construct equivariant and motivic versions of the canonical semiring structure on a symmetric monoidal ![]() $\infty$-category whose tensor product commutes with finite coproducts.
$\infty$-category whose tensor product commutes with finite coproducts.
In the ![]() $G$-equivariant case this structure encodes the compatibility of additive and multiplicative transfers (or norms) along maps of finite
$G$-equivariant case this structure encodes the compatibility of additive and multiplicative transfers (or norms) along maps of finite ![]() $G$-sets. In the case of genuine
$G$-sets. In the case of genuine ![]() $G$-spectra such multiplicative transfers were defined by Hill et al. [Reference Hill, Hopkins and RavenelHHR16] (extending a construction on the level of cohomology groups due to Greenlees and May [Reference Greenlees and MayGM97, Reference BohmannBoh14]) and played a key role in their solution of the Kervaire invariant one problem; more recently, they have been considered as the defining structure of an equivariant symmetric monoidal
$G$-spectra such multiplicative transfers were defined by Hill et al. [Reference Hill, Hopkins and RavenelHHR16] (extending a construction on the level of cohomology groups due to Greenlees and May [Reference Greenlees and MayGM97, Reference BohmannBoh14]) and played a key role in their solution of the Kervaire invariant one problem; more recently, they have been considered as the defining structure of an equivariant symmetric monoidal ![]() $\infty$-category in ongoing work of Barwick et al. [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16].
$\infty$-category in ongoing work of Barwick et al. [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16].
In the motivic version, we have multiplicative transfers along finite étale morphisms and additive transfers along smooth morphisms of schemes. Such multiplicative transfers were constructed for motivic spectra (and in a number of related examples) by Bachmann and Hoyois [Reference Bachmann and HoyoisBH21]. These generalize, among other constructions, Fulton and Macpherson's norms on Chow groups [Reference Fulton and MacPhersonFM87] and Joukhovitski's norms on ![]() $K_0$ (see [Reference JoukhovitskiJou00]).
$K_0$ (see [Reference JoukhovitskiJou00]).
We will also show that the ![]() $\infty$-categories
$\infty$-categories ![]() $\mathrm {Perf}(X)$ of perfect quasicoherent sheaves on a spectral Deligne–Mumford stack
$\mathrm {Perf}(X)$ of perfect quasicoherent sheaves on a spectral Deligne–Mumford stack ![]() $X$ have a similar structure given by a multiplicative pushforward for finite étale maps in addition to the usual pushforward and pullback functors. In all these cases we will obtain the canonical ‘semiring’ structures using a universal property of
$X$ have a similar structure given by a multiplicative pushforward for finite étale maps in addition to the usual pushforward and pullback functors. In all these cases we will obtain the canonical ‘semiring’ structures using a universal property of ![]() $(\infty,2)$-categories of bispans, which is the main result of this paper.
$(\infty,2)$-categories of bispans, which is the main result of this paper.
1.1 Spans and commutative monoids
Before we explain what we mean by bispans, it is helpful to first recall the relation between commutative monoids and spans: if ![]() $\mathbb {F}$ denotes the category of finite sets, then we can define a (2,1)-category
$\mathbb {F}$ denotes the category of finite sets, then we can define a (2,1)-category ![]() $\operatorname {Span}(\mathbb {F})$ where:
$\operatorname {Span}(\mathbb {F})$ where:
• objects are finite sets;
• morphisms from
 $I$ to
$I$ to  $J$ are spans (or correspondences)
$J$ are spans (or correspondences)

• composition is given by pullback, i.e. the composite
is the outer span in the diagram

• 2-morphisms are isomorphisms of spans.
If ![]() $M$ is a commutative monoid in
$M$ is a commutative monoid in ![]() ${\text {Set}}$, we can use the monoid structure to define a functor
${\text {Set}}$, we can use the monoid structure to define a functor
which takes ![]() $I \in \mathbb {F}$ to
$I \in \mathbb {F}$ to ![]() $M^{I} := \prod _{i \in I} M$ and a span
$M^{I} := \prod _{i \in I} M$ and a span ![]() $I \xleftarrow {f} S \xrightarrow {g} J$ to the composite
$I \xleftarrow {f} S \xrightarrow {g} J$ to the composite ![]() $g_{\otimes }f^{*}$ where
$g_{\otimes }f^{*}$ where ![]() $f^{*}\colon M^{I} \to M^{S}$ is given by composition with
$f^{*}\colon M^{I} \to M^{S}$ is given by composition with ![]() $f$ (so
$f$ (so ![]() $f^{*}\phi (s) = \phi (fs)$) and
$f^{*}\phi (s) = \phi (fs)$) and ![]() $g_{\otimes }$ is defined using the product on
$g_{\otimes }$ is defined using the product on ![]() $M$ by
$M$ by
This is compatible with composition of spans, since a pullback square gives a canonical isomorphism of fibres and we have ![]() $(gg')_{\otimes } = g_{\otimes }g'_{\otimes }$ as the multiplication is associative.
$(gg')_{\otimes } = g_{\otimes }g'_{\otimes }$ as the multiplication is associative.
It can be shown that if ![]() $\mathbf {C}$ is any category with finite products, every functor
$\mathbf {C}$ is any category with finite products, every functor ![]() $\Phi \colon \operatorname {Span}(\mathbb {F}) \to \mathbf {C}$ such that
$\Phi \colon \operatorname {Span}(\mathbb {F}) \to \mathbf {C}$ such that ![]() $\Phi (I) \cong \Phi (*)^{\times |I|}$ via the canonical maps arises in this way from a commutative monoid in
$\Phi (I) \cong \Phi (*)^{\times |I|}$ via the canonical maps arises in this way from a commutative monoid in ![]() $\mathbf {C}$. More precisely, we can identify commutative monoids in
$\mathbf {C}$. More precisely, we can identify commutative monoids in ![]() $\mathbf {C}$ with product-preserving functors
$\mathbf {C}$ with product-preserving functors ![]() $\operatorname {Span}(\mathbb {F}) \to \mathbf {C}$. (In other words, the homotopy category of
$\operatorname {Span}(\mathbb {F}) \to \mathbf {C}$. (In other words, the homotopy category of ![]() $\operatorname {Span}(\mathbb {F})$ is precisely the Lawvere theory for commutative monoids.) This is also true homotopically as we now describe.
$\operatorname {Span}(\mathbb {F})$ is precisely the Lawvere theory for commutative monoids.) This is also true homotopically as we now describe.
Theorem 1.1.1 Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $\infty$-category with finite products. There is a natural equivalence of
$\infty$-category with finite products. There is a natural equivalence of ![]() $\infty$-categories between commutative monoids in
$\infty$-categories between commutative monoids in ![]() $\mathcal {C}$ and product-preserving functors
$\mathcal {C}$ and product-preserving functors ![]() $\operatorname {Span}(\mathbb {F}) \to \mathcal {C}$.
$\operatorname {Span}(\mathbb {F}) \to \mathcal {C}$.
The earliest proof of this seems to be the in thesis of Cranch [Reference CranchCra10, Reference CranchCra11]; other proofs (as special cases of different generalizations) are due to Bachmann and Hoyois [Reference Bachmann and HoyoisBH21, Appendix C] and Glasman [Reference GlasmanGla17, Appendix A]. In addition, it appears in Harpaz [Reference HarpazHar20, § 5.2] as the bottom case of his theory of ![]() $m$-commutative monoids.
$m$-commutative monoids.
1.2 Bispans and commutative semirings
We can ask for a similar description for commutative semirings. In this case, we have two operations, addition and multiplication, so we want a ![]() $(2,1)$-category
$(2,1)$-category ![]() ${\text {Bispan}}(\mathbb {F})$ whose objects are again finite sets, with a morphism from
${\text {Bispan}}(\mathbb {F})$ whose objects are again finite sets, with a morphism from ![]() $I$ to
$I$ to ![]() $J$ given by a bispan (or polynomial diagram)
$J$ given by a bispan (or polynomial diagram)

If ![]() $R$ is a commutative semiring in
$R$ is a commutative semiring in ![]() ${\text {Set}}$, we want a functor
${\text {Set}}$, we want a functor
that takes a set ![]() $I$ to
$I$ to ![]() $R^{I}$ and the bispan (
$R^{I}$ and the bispan (
) to ![]() $q_{\oplus }f_{\otimes }p^{*}$ where:
$q_{\oplus }f_{\otimes }p^{*}$ where:
•
 $p^{*} \colon R^{I}\to R^{X}$ is defined by composing with
$p^{*} \colon R^{I}\to R^{X}$ is defined by composing with  $p$,
$p$,
 \[ p^{*}(\phi)(x) = \phi(px); \]
\[ p^{*}(\phi)(x) = \phi(px); \]
•
 $f_{\otimes } \colon R^{X} \to R^{Y}$ is defined by multiplying in
$f_{\otimes } \colon R^{X} \to R^{Y}$ is defined by multiplying in  $R$ fibrewise,
$R$ fibrewise,
 \[ f_{\otimes}(\phi)(y) = \prod_{x \in f^{-1}(y)} \phi(x); \]
\[ f_{\otimes}(\phi)(y) = \prod_{x \in f^{-1}(y)} \phi(x); \]
•
 $q_{\oplus }$ is defined by adding in
$q_{\oplus }$ is defined by adding in  $R$ fibrewise,
$R$ fibrewise,
 \[ q_{\oplus}(\phi)(j) = \sum_{y \in q^{-1}(j)} \phi(y). \]
\[ q_{\oplus}(\phi)(j) = \sum_{y \in q^{-1}(j)} \phi(y). \]
The question is then whether there is a way to define composition of bispans so that this gives a functor. Given a pullback square

in ![]() $\mathbb {F}$, we have identities
$\mathbb {F}$, we have identities ![]() $g_{\otimes }i^{*} = j^{*}f_{\otimes }$ and
$g_{\otimes }i^{*} = j^{*}f_{\otimes }$ and ![]() $g_{\oplus }i^{*} = j^{*}f_{\oplus }$ as before, but now we also need to deal with compositions of the form
$g_{\oplus }i^{*} = j^{*}f_{\oplus }$ as before, but now we also need to deal with compositions of the form ![]() $v_{\otimes }u_{\oplus }$ for
$v_{\otimes }u_{\oplus }$ for ![]() $u \colon I \to J$ and
$u \colon I \to J$ and ![]() $v \colon J \to K$. Using the distributivity of addition over multiplication, for
$v \colon J \to K$. Using the distributivity of addition over multiplication, for ![]() $\phi \colon I \to R$ and
$\phi \colon I \to R$ and ![]() $k \in K$ we can write
$k \in K$ we can write
We can interpret this in terms of a distributivity diagram in ![]() $\mathbb {F}$: if we let
$\mathbb {F}$: if we let ![]() $h \colon X \to K$ be the family of sets
$h \colon X \to K$ be the family of sets ![]() $X_{k} = \prod _{j \in J_{k}} I_{j}$ (so that
$X_{k} = \prod _{j \in J_{k}} I_{j}$ (so that ![]() $h = v_{*}u$ where
$h = v_{*}u$ where ![]() $v_{*}$ is the right adjoint to pullback along
$v_{*}$ is the right adjoint to pullback along ![]() $v$), then the pullback
$v$), then the pullback ![]() $v^{*}X$ has a canonical map to
$v^{*}X$ has a canonical map to ![]() $I$ over
$I$ over ![]() $J$: on the fibre
$J$: on the fibre ![]() $(v^{*}X)_{j}$, which is the product
$(v^{*}X)_{j}$, which is the product ![]() $\prod _{j' \in J_{v(j)}} I_{j'}$, we take the projection to the factor
$\prod _{j' \in J_{v(j)}} I_{j'}$, we take the projection to the factor ![]() $I_{j}$. This gives a commutative diagram
$I_{j}$. This gives a commutative diagram

where the square is cartesian, and we can rewrite the distributivity relation (3) as
This means we will get a functor ![]() ${\text {Bispan}}(\mathbb {F}) \to {\text {Set}}$ from the commutative semiring
${\text {Bispan}}(\mathbb {F}) \to {\text {Set}}$ from the commutative semiring ![]() $R$ if we define the composition of two bispans
$R$ if we define the composition of two bispans
as the outer bispan in the following diagram:

Here we have used a distributivity diagram for ![]() $q$ and the pullback
$q$ and the pullback ![]() $\pi$.
$\pi$.
An explicit construction of a ![]() $(2,1)$-category
$(2,1)$-category ![]() ${\text {Bispan}}(\mathbb {F})$ with this composition is given in the thesis of Cranch [Reference CranchCra10], where it is also proved that this has products (given by the disjoint union of sets), so that we can define commutative semirings in
${\text {Bispan}}(\mathbb {F})$ with this composition is given in the thesis of Cranch [Reference CranchCra10], where it is also proved that this has products (given by the disjoint union of sets), so that we can define commutative semirings in ![]() $\mathcal {S}$ as functors
$\mathcal {S}$ as functors ![]() ${\text {Bispan}}(\mathbb {F}) \to \mathcal {S}$ that preserve finite products. Alternatively, one can relate bispans of finite sets to polynomial functors, which gives an easier definition of
${\text {Bispan}}(\mathbb {F}) \to \mathcal {S}$ that preserve finite products. Alternatively, one can relate bispans of finite sets to polynomial functors, which gives an easier definition of ![]() ${\text {Bispan}}(\mathbb {F})$ (as the complicated composition law (5) corresponds to the ordinary composition of such functors); this approach was carried out by Gambino and Kock [Reference Gambino and KockGK13], who also show that the homotopy category of
${\text {Bispan}}(\mathbb {F})$ (as the complicated composition law (5) corresponds to the ordinary composition of such functors); this approach was carried out by Gambino and Kock [Reference Gambino and KockGK13], who also show that the homotopy category of ![]() ${\text {Bispan}}(\mathbb {F})$ is the Lawvere theory for commutative semirings, so that commutative semirings in an ordinary category
${\text {Bispan}}(\mathbb {F})$ is the Lawvere theory for commutative semirings, so that commutative semirings in an ordinary category ![]() $\mathbf {C}$ with finite products are equivalent to product-preserving functors
$\mathbf {C}$ with finite products are equivalent to product-preserving functors
We expect that the homotopical analogue of this statementFootnote 1 is also true, but this has not yet been proved.
1.3 The universal property of spans
If ![]() $\mathcal {C}$ is a symmetric monoidal
$\mathcal {C}$ is a symmetric monoidal ![]() $\infty$-category such that
$\infty$-category such that ![]() $\mathcal {C}$ has finite coproducts and the tensor product preserves these in each variable, then we expect that
$\mathcal {C}$ has finite coproducts and the tensor product preserves these in each variable, then we expect that ![]() $\mathcal {C}$ has a canonical semiring structure in
$\mathcal {C}$ has a canonical semiring structure in ![]() ${\text {Cat}}_\infty$ with multiplication and addition given by the tensor product and coproduct, respectively. This followsFootnote 2 from the universal property of an
${\text {Cat}}_\infty$ with multiplication and addition given by the tensor product and coproduct, respectively. This followsFootnote 2 from the universal property of an ![]() $(\infty,2)$-category of bispans in
$(\infty,2)$-category of bispans in ![]() $\mathbb {F}$, which is a special case of our main result. Before we state this, it is convenient to first recall the simpler universal property of the
$\mathbb {F}$, which is a special case of our main result. Before we state this, it is convenient to first recall the simpler universal property of the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}(\mathbb {F})$ of spans in
$\operatorname {SPAN}(\mathbb {F})$ of spans in ![]() $\mathbb {F}$, which can be used to prove that an
$\mathbb {F}$, which can be used to prove that an ![]() $\infty$-category with finite coproducts has a canonical symmetric monoidal structure.
$\infty$-category with finite coproducts has a canonical symmetric monoidal structure.
Here ![]() $\operatorname {SPAN}(\mathbb {F})$ has finite sets as objects, spans as morphisms, and morphisms of spans as 2-morphisms, i.e. 2-morphisms are commutative diagrams of the form
$\operatorname {SPAN}(\mathbb {F})$ has finite sets as objects, spans as morphisms, and morphisms of spans as 2-morphisms, i.e. 2-morphisms are commutative diagrams of the form

Suppose ![]() $\mathcal {X}$ is an
$\mathcal {X}$ is an ![]() $(\infty,2)$-category. A functor
$(\infty,2)$-category. A functor ![]() $\Phi \colon \mathbb {F}^{{\text {op}}} \to \mathcal {X}$ is called left adjointable if for every morphism
$\Phi \colon \mathbb {F}^{{\text {op}}} \to \mathcal {X}$ is called left adjointable if for every morphism ![]() $f \colon I \to J$ in
$f \colon I \to J$ in ![]() $\mathbb {F}$, the morphism
$\mathbb {F}$, the morphism ![]() $f^{\circledast } := \Phi (f) \colon \Phi (J) \to \Phi (I)$ in
$f^{\circledast } := \Phi (f) \colon \Phi (J) \to \Phi (I)$ in ![]() $\mathcal {X}$ has a left adjoint
$\mathcal {X}$ has a left adjoint ![]() $f_{\oplus }$, and for every pullback square (2) in
$f_{\oplus }$, and for every pullback square (2) in ![]() $\mathbb {F}$, the canonical (Beck–Chevalley or mate) transformation
$\mathbb {F}$, the canonical (Beck–Chevalley or mate) transformation
is an equivalence.
Theorem 1.3.1 Restricting along the inclusion ![]() $\mathbb {F}^{{\text {op}}} \to \operatorname {SPAN}(\mathbb {F})$ (of the subcategory containing only the backwards maps and no non-trivial 2-morphisms) gives a natural equivalence between functors
$\mathbb {F}^{{\text {op}}} \to \operatorname {SPAN}(\mathbb {F})$ (of the subcategory containing only the backwards maps and no non-trivial 2-morphisms) gives a natural equivalence between functors ![]() $\operatorname {SPAN}(\mathbb {F}) \to \mathcal {X}$ and left adjointable functors
$\operatorname {SPAN}(\mathbb {F}) \to \mathcal {X}$ and left adjointable functors ![]() $\mathbb {F}^{{\text {op}}} \to \mathcal {X}$.
$\mathbb {F}^{{\text {op}}} \to \mathcal {X}$.
This is a special case of a recent result of Macpherson [Reference MacphersonMac22], which we review in more generality below in § 2.2. Another proof is sketched in the book of Gaitsgory and Rozenblyum [Reference Gaitsgory and RozenblyumGR17] where this universal property is used to encode a ‘six-functor formalism’ for various categories of quasicoherent sheaves on derived schemes. Lastly, we note that the analogous result for ordinary 2-categories seems to have been first proved by Hermida [Reference HermidaHer00, Theorem A.2].
1.4 The universal property of bispans
We now want to consider a 2-category ![]() ${\text {BISPAN}}(\mathbb {F})$ whose objects are finite sets, with morphisms given by bispans and 2-morphisms by commutative diagrams of the form
${\text {BISPAN}}(\mathbb {F})$ whose objects are finite sets, with morphisms given by bispans and 2-morphisms by commutative diagrams of the form

where the middle square is cartesian. If we look at the subcategory where the morphisms are bispans whose rightmost leg is invertible and with no non-trivial 2-morphisms, we get an inclusion ![]() $\operatorname {Span}(\mathbb {F}) \to {\text {BISPAN}}(\mathbb {F})$. A special case of our main result gives a universal property of
$\operatorname {Span}(\mathbb {F}) \to {\text {BISPAN}}(\mathbb {F})$. A special case of our main result gives a universal property of ![]() ${\text {BISPAN}}(\mathbb {F})$ in terms of this subcategory as follows.
${\text {BISPAN}}(\mathbb {F})$ in terms of this subcategory as follows.
Theorem 1.4.1 Let ![]() $\mathcal {X}$ be an
$\mathcal {X}$ be an ![]() $(\infty,2)$-category. Restricting along the inclusion
$(\infty,2)$-category. Restricting along the inclusion ![]() $\operatorname {Span}(\mathbb {F}) \to {\text {BISPAN}}(\mathbb {F})$ gives an equivalence between functors
$\operatorname {Span}(\mathbb {F}) \to {\text {BISPAN}}(\mathbb {F})$ gives an equivalence between functors ![]() ${\text {BISPAN}}(\mathbb {F}) \to \mathcal {X}$ and distributive functors
${\text {BISPAN}}(\mathbb {F}) \to \mathcal {X}$ and distributive functors ![]() $\operatorname {Span}(\mathbb {F}) \to \mathcal {X}$.
$\operatorname {Span}(\mathbb {F}) \to \mathcal {X}$.
Here a functor ![]() $\Phi \colon \operatorname {Span}(\mathbb {F}) \to \mathcal {X}$ is distributive if:
$\Phi \colon \operatorname {Span}(\mathbb {F}) \to \mathcal {X}$ is distributive if:
• for every morphism
 $f \colon I \to J$ in
$f \colon I \to J$ in  $\mathbb {F}$, the morphism
$\mathbb {F}$, the morphism  $f^{\circledast } := \Phi (J \xleftarrow {f} I == {\,\,} I)$ in
$f^{\circledast } := \Phi (J \xleftarrow {f} I == {\,\,} I)$ in  $\mathcal {X}$ has a left adjoint
$\mathcal {X}$ has a left adjoint  $f_{\oplus }$;
$f_{\oplus }$;• for every pullback square (2) in
 $\mathbb {F}$, the Beck–Chevalley transformation
$\mathbb {F}$, the Beck–Chevalley transformation  $g_{\oplus }i^{\circledast } \to j^{\circledast }f_{\oplus }$ is an equivalence;
$g_{\oplus }i^{\circledast } \to j^{\circledast }f_{\oplus }$ is an equivalence;• for every distributivity diagram (4), the distributivity transformation
which is defined as a certain composite of units and counits, is an equivalence in \[ h_{\oplus}\tilde{v}_{\otimes}\epsilon^{\circledast} \to v_{\otimes}u_{\oplus}, \]
\[ h_{\oplus}\tilde{v}_{\otimes}\epsilon^{\circledast} \to v_{\otimes}u_{\oplus}, \]
 $\mathcal {X}$.
$\mathcal {X}$.
Note that the only property of ![]() $\mathbb {F}$ we have used in the definition of distributive functors is the existence of distributivity diagrams. These exist in any locally cartesian closed
$\mathbb {F}$ we have used in the definition of distributive functors is the existence of distributivity diagrams. These exist in any locally cartesian closed ![]() $\infty$-category, and more generally we can consider triples
$\infty$-category, and more generally we can consider triples ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consisting of an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consisting of an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ with a pair of subcategories
$\mathcal {C}$ with a pair of subcategories ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $\mathcal {C}_{L}$ such that:
$\mathcal {C}_{L}$ such that:
• pullbacks along morphisms in
 $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and  $\mathcal {C}_{L}$ exist in
$\mathcal {C}_{L}$ exist in  $\mathcal {C}$, and both subcategories are preserved under base change;
$\mathcal {C}$, and both subcategories are preserved under base change;• there exist suitable distributivity diagrams in
 $\mathcal {C}$ for any composable pair of morphisms
$\mathcal {C}$ for any composable pair of morphisms  $l \colon x \to y$ in
$l \colon x \to y$ in  $\mathcal {C}_{L}$,
$\mathcal {C}_{L}$,  $f \colon y \to z$ in
$f \colon y \to z$ in  $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
We can then generalize the notion of distributive functors above to that of ![]() $L$-distributive functors
$L$-distributive functors ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$, where
$\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$, where ![]() $\operatorname {Span}_{F}(\mathcal {C})$ is the
$\operatorname {Span}_{F}(\mathcal {C})$ is the ![]() $\infty$-category of spans in
$\infty$-category of spans in ![]() $\mathcal {C}$ whose forward legs are required to lie in
$\mathcal {C}$ whose forward legs are required to lie in ![]() $\mathcal {C}_{F}$. Our main result in this paper is then the following generalization of Theorem 1.4.1.
$\mathcal {C}_{F}$. Our main result in this paper is then the following generalization of Theorem 1.4.1.
Theorem 1.4.2 For ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ as above, there exists an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ as above, there exists an ![]() $(\infty,2)$-category
$(\infty,2)$-category
such that:
• objects are objects of
 $\mathcal {C}$;
$\mathcal {C}$;• morphisms are bispans
where \[ x \xleftarrow{p} e \xrightarrow{f} b \xrightarrow{l} y \]
\[ x \xleftarrow{p} e \xrightarrow{f} b \xrightarrow{l} y \]
 $f$ is in
$f$ is in  $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and  $l$ is in
$l$ is in  $\mathcal {C}_{L}$;
$\mathcal {C}_{L}$;• 2-morphisms are diagrams of the form (6);
• morphisms compose as in (5).
The ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ has the universal property that restricting to the subcategory
${\text {BISPAN}}_{F,L}(\mathcal {C})$ has the universal property that restricting to the subcategory ![]() $\operatorname {Span}_{F}(\mathcal {C})$ gives for any
$\operatorname {Span}_{F}(\mathcal {C})$ gives for any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$ an equivalence between functors
$\mathcal {X}$ an equivalence between functors ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C}) \to \mathcal {X}$ and
${\text {BISPAN}}_{F,L}(\mathcal {C}) \to \mathcal {X}$ and ![]() $L$-distributive functors
$L$-distributive functors ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$.
$\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$.
The analogue of this result for ordinary 2-categories (at least in the case where ![]() $\mathcal {C} = \mathcal {C}_{F} = \mathcal {C}_{L}$) is due to Walker [Reference WalkerWal19].
$\mathcal {C} = \mathcal {C}_{F} = \mathcal {C}_{L}$) is due to Walker [Reference WalkerWal19].
1.5 Equivariant and algebro-geometric bispans
We now look briefly at some examples of Theorem 1.4.2 beyond the case of finite sets, coming from equivariant and motivic homotopy theory and derived algebraic geometry. These examples are discussed in more detail in § 3.
Let us first consider the equivariant setting, over a finite group ![]() $G$. In all of our discussion above it is straightforward to replace the category
$G$. In all of our discussion above it is straightforward to replace the category ![]() $\mathbb {F}$ of finite sets with the category
$\mathbb {F}$ of finite sets with the category ![]() $\mathbb {F}_{G}$ of finite
$\mathbb {F}_{G}$ of finite ![]() $G$-sets. The analogue of a commutative monoid is then a functor
$G$-sets. The analogue of a commutative monoid is then a functor
that preserves products. This is (essentiallyFootnote 3) the same thing as a Mackey functor [Reference DressDre71], an algebraic structure where for a subgroup ![]() $H \subseteq G$ we have restrictions
$H \subseteq G$ we have restrictions ![]() $M^{G} \to M^{H}$ and transfers
$M^{G} \to M^{H}$ and transfers ![]() $M^{H} \to M^{G}$ satisfying a base change property that can be interpreted in terms of double cosets. Mackey functors play an important role in group theory, and every genuine
$M^{H} \to M^{G}$ satisfying a base change property that can be interpreted in terms of double cosets. Mackey functors play an important role in group theory, and every genuine ![]() $G$-spectrum
$G$-spectrum ![]() $E$ has an underlying Mackey functor
$E$ has an underlying Mackey functor ![]() $\pi _{0}E$.
$\pi _{0}E$.
Similarly, the ![]() $G$-analogue of a commutative semiring is a product-preserving functor
$G$-analogue of a commutative semiring is a product-preserving functor ![]() ${\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Set}}$, which is essentiallyFootnote 4 a Tambara functor [Reference TambaraTam93, Reference StricklandStr12, Reference Blumberg and HillBH18]. This is a structure that has both an ‘additive’ and a ‘multiplicative’ transfer, satisfying a distributivity relation. If
${\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Set}}$, which is essentiallyFootnote 4 a Tambara functor [Reference TambaraTam93, Reference StricklandStr12, Reference Blumberg and HillBH18]. This is a structure that has both an ‘additive’ and a ‘multiplicative’ transfer, satisfying a distributivity relation. If ![]() $E$ is a genuine
$E$ is a genuine ![]() $G$-
$G$-![]() $E_{\infty }$-ring spectrum, then
$E_{\infty }$-ring spectrum, then ![]() $\pi _{0}E$ has the structure of a Tambara functor [Reference BrunBru07].
$\pi _{0}E$ has the structure of a Tambara functor [Reference BrunBru07].
If we replace the category of sets with the ![]() $\infty$-category of spaces, a theorem of NardinFootnote 5 [Reference NardinNar16, Corollary A.4.1] shows that connective
$\infty$-category of spaces, a theorem of NardinFootnote 5 [Reference NardinNar16, Corollary A.4.1] shows that connective ![]() $G$-spectra are equivalently product-preserving functors
$G$-spectra are equivalently product-preserving functors ![]() $\operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {S}$ that are grouplike, generalizing the classical description of connective spectra as grouplike commutative monoids in
$\operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {S}$ that are grouplike, generalizing the classical description of connective spectra as grouplike commutative monoids in ![]() $\mathcal {S}$.Footnote 6
$\mathcal {S}$.Footnote 6
The analogue for ring spectra is also expected to hold: connective genuine ![]() $G$-
$G$-![]() $E_{\infty }$-ring spectra should be equivalent to product-preserving functors
$E_{\infty }$-ring spectra should be equivalent to product-preserving functors ![]() ${\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$.
${\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$.
Now we turn to the ‘categorified’ versions of these structures: for ![]() $H$ a subgroup of
$H$ a subgroup of ![]() $G$, the (additive) transfer from
$G$, the (additive) transfer from ![]() $H$-spectra to
$H$-spectra to ![]() $G$-spectra is classical,Footnote 7 but the multiplicative transfer or norm was only introduced fairly recently by Hill, Hopkins, and Ravenel as part of the foundational setup for [Reference Hill, Hopkins and RavenelHHR16]. This inspired a plethora of work on equivariant symmetric monoidal structures [Reference Hopkins and HillHH16, Reference Guillou, May, Merling and OsornoGMMO20, Reference RubinRub17] and its relation to equivariant homotopy-coherent commutativity (in particular, [Reference Blumberg and HillBH15] and subsequent work on
$G$-spectra is classical,Footnote 7 but the multiplicative transfer or norm was only introduced fairly recently by Hill, Hopkins, and Ravenel as part of the foundational setup for [Reference Hill, Hopkins and RavenelHHR16]. This inspired a plethora of work on equivariant symmetric monoidal structures [Reference Hopkins and HillHH16, Reference Guillou, May, Merling and OsornoGMMO20, Reference RubinRub17] and its relation to equivariant homotopy-coherent commutativity (in particular, [Reference Blumberg and HillBH15] and subsequent work on ![]() $N_{\infty }$-operads), culminating from our point of view in the approach of Barwick et al. [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16], where a
$N_{\infty }$-operads), culminating from our point of view in the approach of Barwick et al. [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16], where a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category can be viewed as a product-preserving functor
$\infty$-category can be viewed as a product-preserving functor
i.e. a ‘categorified Mackey functor’.
If the contravariant (restriction) functors have left adjoints that satisfy base change and distributivity, Theorem 1.4.2 allows us to upgrade such ![]() $G$-symmetric monoidal structures to functors from
$G$-symmetric monoidal structures to functors from ![]() ${\text {BISPAN}}(\mathbb {F}_{G})$, which encodes the distributive compatibility of multiplicative and additive transfers. We will see that this applies, in particular, to genuine
${\text {BISPAN}}(\mathbb {F}_{G})$, which encodes the distributive compatibility of multiplicative and additive transfers. We will see that this applies, in particular, to genuine ![]() $G$-spectra, giving a ‘categorified Tambara functor’ structure on
$G$-spectra, giving a ‘categorified Tambara functor’ structure on ![]() $G$-spectra.
$G$-spectra.
Next, we look at the motivic setting, where it is more instructive to first work in the categorified context. By this we mean Ayoub's construction of a functor from schemes to categories ![]() $X \mapsto \mathrm {SH}(X)$ which satisfies a full six functors formalism [Reference AyoubAyo07], vastly expanding Voevodsky's notes in [Reference VoevodskyVoe99]; we also refer the reader to the book of Cisinski and Déglise [Reference Cisinski and DégliseCD19] for another exposition, [Reference HoyoisHoy17] for an
$X \mapsto \mathrm {SH}(X)$ which satisfies a full six functors formalism [Reference AyoubAyo07], vastly expanding Voevodsky's notes in [Reference VoevodskyVoe99]; we also refer the reader to the book of Cisinski and Déglise [Reference Cisinski and DégliseCD19] for another exposition, [Reference HoyoisHoy17] for an ![]() $\infty$-categorical enhancement of this construction in the more general motivic-equivariant setting, as well as the more recent [Reference Drew and GallauerDG22] for a universal property of this construction. Here
$\infty$-categorical enhancement of this construction in the more general motivic-equivariant setting, as well as the more recent [Reference Drew and GallauerDG22] for a universal property of this construction. Here ![]() $\mathrm {SH}(X)$ denotes the
$\mathrm {SH}(X)$ denotes the ![]() $\infty$-category of motivic spectra over a scheme
$\infty$-category of motivic spectra over a scheme ![]() $X$.
$X$.
In this context, given a smooth morphism of schemes ![]() $f \colon X \rightarrow Y$ over a base
$f \colon X \rightarrow Y$ over a base ![]() $S$, the pullback functor
$S$, the pullback functor ![]() $f^* \colon \mathrm {SH}(Y) \rightarrow \mathrm {SH}(X)$ admits a left adjoint,
$f^* \colon \mathrm {SH}(Y) \rightarrow \mathrm {SH}(X)$ admits a left adjoint, ![]() $f_{\sharp } \colon \mathrm {SH}(X) \rightarrow \mathrm {SH}(Y)$. This is a categorified version of the additive pushforward: if
$f_{\sharp } \colon \mathrm {SH}(X) \rightarrow \mathrm {SH}(Y)$. This is a categorified version of the additive pushforward: if ![]() $f$ is the fold map
$f$ is the fold map ![]() $\nabla \colon Y^{\amalg I} \rightarrow Y$, then
$\nabla \colon Y^{\amalg I} \rightarrow Y$, then ![]() $\nabla _{\sharp }$ computes the
$\nabla _{\sharp }$ computes the ![]() $I$-indexed direct sum. The compatibility of
$I$-indexed direct sum. The compatibility of ![]() $f_{\sharp }$ with pullbacks yields a functor
$f_{\sharp }$ with pullbacks yields a functor
An important additional functoriality of ![]() $\mathrm {SH}$ was recently discovered by Bachmann and Hoyois in [Reference Bachmann and HoyoisBH21]: given a finite étale morphism
$\mathrm {SH}$ was recently discovered by Bachmann and Hoyois in [Reference Bachmann and HoyoisBH21]: given a finite étale morphism ![]() $f \colon X \rightarrow Y$ we have the multiplicative pushforward or norm
$f \colon X \rightarrow Y$ we have the multiplicative pushforward or norm ![]() $f_{\otimes } \colon \mathrm {SH}(X) \rightarrow \mathrm {SH}(Y)$, which in the case when
$f_{\otimes } \colon \mathrm {SH}(X) \rightarrow \mathrm {SH}(Y)$, which in the case when ![]() $f$ is the fold map computes the
$f$ is the fold map computes the ![]() $I$-indexed tensor product. This also satisfies base change, and so can be encoded by a functor
$I$-indexed tensor product. This also satisfies base change, and so can be encoded by a functor
which leads to the correct notion of a coherent multiplicative structure in motivic homotopy theory, a normed motivic spectrum, as a section of the unstraightening of (8) that is cocartesian over the backwards maps in ![]() $\operatorname {Span}_{\text {f} {\unicode{x00E8}} \text{t}}(\mathrm {Sch}_{S})$.
$\operatorname {Span}_{\text {f} {\unicode{x00E8}} \text{t}}(\mathrm {Sch}_{S})$.
The motivic bispan category should combine these two structures, giving an additive pushforward along smooth morphisms and a multiplicative pushforward along finite étale morphisms. For technical reasons (due to the non-existence of Weil restriction of schemes in general), for our motivic bispan categories we either have to restrict to morphisms between schemes that are smooth and quasiprojective or work with algebraic spaces. Thus, we consider 2-categories of the form ![]() ${\text {BISPAN}}_{\text {f} {\unicode{x00E8}} \text{t}},\mathrm {sm}(\mathrm {AlgSpc}_{S})$ where
${\text {BISPAN}}_{\text {f} {\unicode{x00E8}} \text{t}},\mathrm {sm}(\mathrm {AlgSpc}_{S})$ where ![]() $\mathrm {AlgSpc}_{S}$ means the category of algebraic spaces over
$\mathrm {AlgSpc}_{S}$ means the category of algebraic spaces over ![]() $S$, and we promote
$S$, and we promote ![]() $\mathrm {SH}$ to a functor
$\mathrm {SH}$ to a functor
see Theorem 3.5.9.
The decategorification of the above structure has been studied by Bachmann in [Reference BachmannBac21]. Working over a field, and restricting to a category of bispans between smooth schemes, ![]() ${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},\mathrm {sm}(\mathrm {Sm}_{k})$, Bachmann proved that the structure of a normed algebra in the abelian category of homotopy modules (the heart of the so-called homotopy
${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},\mathrm {sm}(\mathrm {Sm}_{k})$, Bachmann proved that the structure of a normed algebra in the abelian category of homotopy modules (the heart of the so-called homotopy ![]() $t$-structure on motivic spectra) is encoded by certain functors out of this bispan category to abelian groups (appropriately christened motivic Tambara functors), at least after inverting the exponential characteristic of
$t$-structure on motivic spectra) is encoded by certain functors out of this bispan category to abelian groups (appropriately christened motivic Tambara functors), at least after inverting the exponential characteristic of ![]() $k$.
$k$.
We also note that there is a discrepancy with the classical and finite-equivariant story: finite étale transfers are a priori not sufficient to encode the structure of a motivic spectrum. Instead, the correct kind of transfers are framed transfers in the sense of [Reference Elmanto, Hoyois, Khan, Sosnilo and YakersonEHK+21]. In particular, the category of framed correspondences, where the backward maps encode framed transfers, is manifestly an ![]() $\infty$-category. In other words, the additive and multiplicative transfers are rather different in the motivic story; for example, we do not know if the space of units of a normed motivic spectrum has framed transfers (see [Reference Bachmann and HoyoisBH21, § 1.5] for a discussion). For us, this means that a more robust theory of bispans in the motivic setting which encodes framed transfers is open for future investigations.
$\infty$-category. In other words, the additive and multiplicative transfers are rather different in the motivic story; for example, we do not know if the space of units of a normed motivic spectrum has framed transfers (see [Reference Bachmann and HoyoisBH21, § 1.5] for a discussion). For us, this means that a more robust theory of bispans in the motivic setting which encodes framed transfers is open for future investigations.
Finally, we consider an example in the context of derived algebraic geometry: If ![]() $\mathrm {Perf}(X)$ denotes the
$\mathrm {Perf}(X)$ denotes the ![]() $\infty$-category of perfect quasicoherent sheaves on a spectral Deligne–Mumford stack, Barwick [Reference BarwickBar17] has shown that the pullback and pushforward functors extend to a functor
$\infty$-category of perfect quasicoherent sheaves on a spectral Deligne–Mumford stack, Barwick [Reference BarwickBar17] has shown that the pullback and pushforward functors extend to a functor
where ![]() $\mathrm {SpDM}$ is the
$\mathrm {SpDM}$ is the ![]() $\infty$-category of spectral Deligne–Mumford stacks and
$\infty$-category of spectral Deligne–Mumford stacks and ![]() $\mathcal {FP}$ is a certain class of morphisms (for which pushforwards preserve perfect objects and base change is satisfied). We promote this to a functor of
$\mathcal {FP}$ is a certain class of morphisms (for which pushforwards preserve perfect objects and base change is satisfied). We promote this to a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
using a multiplicative pushforward functor for finite étale maps (which exists by results of Bachmann and Hoyois [Reference Bachmann and HoyoisBH21]), where ![]() $\mathcal {FP}'$ is a certain subclass of
$\mathcal {FP}'$ is a certain subclass of ![]() $\mathcal {FP}$ for which Weil restrictions exist.
$\mathcal {FP}$ for which Weil restrictions exist.
1.6 Norms in algebraic  $K$-theory
$K$-theory
A combination of the present work and [Reference Barwick, Glasman, Mathew and NikolausBGMN21] produces concrete examples of Tambara functors valued in ![]() $\mathcal {S}$, the
$\mathcal {S}$, the ![]() $\infty$-category of spaces, via (connective) algebraic
$\infty$-category of spaces, via (connective) algebraic ![]() $K$-theory, which we discuss in § 4. The motivation for our results traces back to classical representation theory: given a finite group
$K$-theory, which we discuss in § 4. The motivation for our results traces back to classical representation theory: given a finite group ![]() $G$, the classical representation ring of
$G$, the classical representation ring of ![]() $G$ is a certain Grothendieck ring:
$G$ is a certain Grothendieck ring:
In particular, the tensor product of representations induces the multiplicative structure on ![]() $\mathrm {Rep}(G,\mathbb {C})$. It is natural to consider the formation of representation rings as a functor in
$\mathrm {Rep}(G,\mathbb {C})$. It is natural to consider the formation of representation rings as a functor in ![]() $G$, where the functoriality encodes various operations in representation theory such as induction and restrictions. From this viewpoint, one can enhance the multiplicative structure on
$G$, where the functoriality encodes various operations in representation theory such as induction and restrictions. From this viewpoint, one can enhance the multiplicative structure on ![]() $\mathrm {Rep}(G,\mathbb {C})$ to one parametrized by cosets: if
$\mathrm {Rep}(G,\mathbb {C})$ to one parametrized by cosets: if ![]() $K \subset G$ is a subgroup, then we have a map given by the operation of tensor induction:
$K \subset G$ is a subgroup, then we have a map given by the operation of tensor induction:
As reviewed in Example 3.4.18, all of this functoriality can be encoded as a functor out of a bispan category formed out of finite ![]() $G$-sets.
$G$-sets.
Representation theory with ‘fancy coefficients’ entails replacing the category ![]() $\mathrm {Vect}^{\mathrm {fd}}_{\mathbb {C}}$ with a more sophisticated symmetric monoidal (
$\mathrm {Vect}^{\mathrm {fd}}_{\mathbb {C}}$ with a more sophisticated symmetric monoidal (![]() $\infty$-)category
$\infty$-)category ![]() $\mathcal {C}$. This line of investigation arguably began with the subject of modular representation theory, which takes
$\mathcal {C}$. This line of investigation arguably began with the subject of modular representation theory, which takes ![]() $\mathcal {C}$ to be
$\mathcal {C}$ to be ![]() $\mathrm {Vect}^{\mathrm {fd}}_{\mathbb {F}_p}$. This is especially subtle when
$\mathrm {Vect}^{\mathrm {fd}}_{\mathbb {F}_p}$. This is especially subtle when ![]() $G$ is a
$G$ is a ![]() $p$-group because of the failure of the category
$p$-group because of the failure of the category ![]() ${\text {Fun}}(BG, {\text {Vect}}^{\mathrm {fd}}_{\mathbb {F}_p})$ to be semisimple. More recently, Treumann has also considered replacing vector spaces with
${\text {Fun}}(BG, {\text {Vect}}^{\mathrm {fd}}_{\mathbb {F}_p})$ to be semisimple. More recently, Treumann has also considered replacing vector spaces with ![]() $KU$-module spectra, thus taking
$KU$-module spectra, thus taking ![]() $\mathcal {C}$ to be
$\mathcal {C}$ to be ![]() $\mathrm {Perf}_{\mathrm {KU}}$ where
$\mathrm {Perf}_{\mathrm {KU}}$ where ![]() $KU$ is the
$KU$ is the ![]() $\mathbb {E}_{\infty }$-ring spectrum representing complex topological
$\mathbb {E}_{\infty }$-ring spectrum representing complex topological ![]() $K$-theory [Reference TreumannTre15]; his work suggests that, up to
$K$-theory [Reference TreumannTre15]; his work suggests that, up to ![]() $p$-completion, representation theory over
$p$-completion, representation theory over ![]() $KU$ is, in a precise way, a smooth deformation of representation theory over the
$KU$ is, in a precise way, a smooth deformation of representation theory over the ![]() $p$-adic integers [Reference TreumannTre15, 1.7].
$p$-adic integers [Reference TreumannTre15, 1.7].
In light of the last example, which is homotopical in nature, it is natural to consider the ![]() $K$-theory space
$K$-theory space ![]() $\Omega ^{\infty }K({\text {Fun}}(BG, \mathcal {C}))$ for
$\Omega ^{\infty }K({\text {Fun}}(BG, \mathcal {C}))$ for ![]() $\mathcal {C}$ a small stable
$\mathcal {C}$ a small stable ![]() $\infty$-category; its homotopy groups are the higher
$\infty$-category; its homotopy groups are the higher ![]() $K$-groups. Using the universal property of bispans, coupled with the main result of [Reference Barwick, Glasman, Mathew and NikolausBGMN21], we offer the following result concerning its functoriality in the variable
$K$-groups. Using the universal property of bispans, coupled with the main result of [Reference Barwick, Glasman, Mathew and NikolausBGMN21], we offer the following result concerning its functoriality in the variable ![]() $G$.
$G$.
Theorem 1.6.1 Let ![]() $G$ be a finite group and
$G$ be a finite group and ![]() $\mathcal {C}$ a symmetric monoidal
$\mathcal {C}$ a symmetric monoidal ![]() $\infty$-category, then the presheaf on
$\infty$-category, then the presheaf on ![]() $G$-orbits:
$G$-orbits:
extends canonically as

The proof of Theorem 1.6.1 is quite simple given our main theorem: we use this to deduce that ![]() ${\text {Fun}}(BG,\mathcal {C})$ upgrades to a functor out of bispans into the
${\text {Fun}}(BG,\mathcal {C})$ upgrades to a functor out of bispans into the ![]() $\infty$-category of
$\infty$-category of ![]() $\infty$-categories. Using a general criterion which we detail in § 4.2, we prove that the multiplicative pushforward enjoys the property of being a polynomial functor in the sense of Goodwillie calculus. A recent breakthrough of Barwick et al. [Reference Barwick, Glasman, Mathew and NikolausBGMN21] proves that the formation of algebraic
$\infty$-categories. Using a general criterion which we detail in § 4.2, we prove that the multiplicative pushforward enjoys the property of being a polynomial functor in the sense of Goodwillie calculus. A recent breakthrough of Barwick et al. [Reference Barwick, Glasman, Mathew and NikolausBGMN21] proves that the formation of algebraic ![]() $K$-theory spaces is functorial in polynomial functors, which then gives Theorem 1.6.1.
$K$-theory spaces is functorial in polynomial functors, which then gives Theorem 1.6.1.
We believe that Theorem 1.6.1 could have computational significance. Using an equivariant analogue of [Reference Bachmann and HoyoisBH21, Example 7.25], Theorem 1.6.1 produces genuine-equivariant power operations on these representation-theoretic gadgets. In particular, the coherence afforded by the language of bispans results in relations between these operations.
By exactly the same methods we also show that the algebraic ![]() $K$-theory of a genuine
$K$-theory of a genuine ![]() $G$-
$G$-![]() $E_{\infty }$-ring spectrum is also a Tambara functor valued in
$E_{\infty }$-ring spectrum is also a Tambara functor valued in ![]() $\mathcal {S}$. The latter are expected to be precisely the connective
$\mathcal {S}$. The latter are expected to be precisely the connective ![]() $G$-
$G$-![]() $E_{\infty }$-ring spectra, and given this we prove the following result.
$E_{\infty }$-ring spectra, and given this we prove the following result.
Theorem 1.6.2 (see Theorem 4.3.7)
The formation of algebraic ![]() $K$-theory preserves
$K$-theory preserves ![]() $G$-
$G$-![]() $E_{\infty }$-rings.
$E_{\infty }$-rings.
We believe this is a completely new structure on algebraic ![]() $K$-theory in equivariant homotopy theory that significantly extends several recent results in the literature; see Remark 4.3.8.
$K$-theory in equivariant homotopy theory that significantly extends several recent results in the literature; see Remark 4.3.8.
In the algebro-geometric context the same method also shows that, for instance, the algebraic ![]() $K$-theory of schemes (or more generally spectral Deligne–Mumford stacks) has multiplicative transfers along finite étale morphisms.
$K$-theory of schemes (or more generally spectral Deligne–Mumford stacks) has multiplicative transfers along finite étale morphisms.
1.7 Notation
This paper is written in the language of ![]() $\infty$-categories. We use the following reasonably standard notation:
$\infty$-categories. We use the following reasonably standard notation:
•
 $\mathcal {S}$ is the
$\mathcal {S}$ is the  $\infty$-category of spaces, i.e.
$\infty$-category of spaces, i.e.  $\infty$-groupoids;
$\infty$-groupoids;•
 ${\text {Cat}}_\infty$ is the
${\text {Cat}}_\infty$ is the  $\infty$-category of
$\infty$-category of  $\infty$-categories;
$\infty$-categories;•
 ${\text {CAT}}_{\infty }$ is the
${\text {CAT}}_{\infty }$ is the  $(\infty,2)$-category of
$(\infty,2)$-category of  $\infty$-categories;
$\infty$-categories;•
 ${\text {Cat}}_{(\infty,2)}$ is the
${\text {Cat}}_{(\infty,2)}$ is the  $\infty$-category of
$\infty$-category of  $(\infty,2)$-categories;
$(\infty,2)$-categories;• if
 $\mathcal {C}$ and
$\mathcal {C}$ and  $\mathcal {D}$ are
$\mathcal {D}$ are  $\infty$-categories or
$\infty$-categories or  $(\infty,2)$-categories, we write
$(\infty,2)$-categories, we write  ${\text {Fun}}(\mathcal {C},\mathcal {D})$ for the
${\text {Fun}}(\mathcal {C},\mathcal {D})$ for the  $\infty$-category of functors from
$\infty$-category of functors from  $\mathcal {C}$ to
$\mathcal {C}$ to  $\mathcal {D}$;
$\mathcal {D}$;• if
 $\mathcal {C}$ and
$\mathcal {C}$ and  $\mathcal {D}$ are
$\mathcal {D}$ are  $(\infty,2)$-categories, we write
$(\infty,2)$-categories, we write  ${\text {FUN}}(\mathcal {C},\mathcal {D})$ for the
${\text {FUN}}(\mathcal {C},\mathcal {D})$ for the  $(\infty,2)$-category of functors from
$(\infty,2)$-category of functors from  $\mathcal {C}$ to
$\mathcal {C}$ to  $\mathcal {D}$;
$\mathcal {D}$;• we write
 $(-)^{(1)} \colon {\text {Cat}}_{(\infty,2)} \to {\text {Cat}}_\infty$ for the functor taking an
$(-)^{(1)} \colon {\text {Cat}}_{(\infty,2)} \to {\text {Cat}}_\infty$ for the functor taking an  $(\infty,2)$-category to its underlying
$(\infty,2)$-category to its underlying  $\infty$-category (thus,
$\infty$-category (thus,  $(-)^{(1)}$ is right adjoint to the inclusion of
$(-)^{(1)}$ is right adjoint to the inclusion of  ${\text {Cat}}_\infty$ into
${\text {Cat}}_\infty$ into  ${\text {Cat}}_{(\infty,2)}$);
${\text {Cat}}_{(\infty,2)}$);• we write
 $(-)^{\simeq }$ for the functors
$(-)^{\simeq }$ for the functors  ${\text {Cat}}_\infty \to \mathcal {S}$ and
${\text {Cat}}_\infty \to \mathcal {S}$ and  ${\text {Cat}}_{(\infty,2)} \to \mathcal {S}$ taking an
${\text {Cat}}_{(\infty,2)} \to \mathcal {S}$ taking an  $\infty$-category or
$\infty$-category or  $(\infty,2)$-category to its underlying
$(\infty,2)$-category to its underlying  $\infty$-groupoid;
$\infty$-groupoid;• if
 $\mathcal {C}$ is an
$\mathcal {C}$ is an  $\infty$-category and
$\infty$-category and  $x$ and
$x$ and  $y$ are objects of
$y$ are objects of  $\mathcal {C}$, we write
$\mathcal {C}$, we write  ${\text {Map}}_{\mathcal {C}}(x,y)$ for the space of maps from
${\text {Map}}_{\mathcal {C}}(x,y)$ for the space of maps from  $x$ to
$x$ to  $y$ in
$y$ in  $\mathcal {C}$;
$\mathcal {C}$;• if
 $\mathcal {C}$ is an
$\mathcal {C}$ is an  $(\infty,2)$-category and
$(\infty,2)$-category and  $x$ and
$x$ and  $y$ are objects of
$y$ are objects of  $\mathcal {C}$, we write
$\mathcal {C}$, we write  ${\text {MAP}}_{\mathcal {C}}(x,y)$ for the
${\text {MAP}}_{\mathcal {C}}(x,y)$ for the  $\infty$-category of maps from
$\infty$-category of maps from  $x$ to
$x$ to  $y$ in
$y$ in  $\mathcal {C}$;
$\mathcal {C}$;• if
 $\mathcal {X}$ is an
$\mathcal {X}$ is an  $(\infty,2)$-category we write
$(\infty,2)$-category we write  $\mathcal {X}^{{\text {op}}}$ for the
$\mathcal {X}^{{\text {op}}}$ for the  $(\infty,2)$-category obtained by reversing the morphisms in
$(\infty,2)$-category obtained by reversing the morphisms in  $\mathcal {X}$ and
$\mathcal {X}$ and  $\mathcal {X}^{2{\text {-op}}}$ for that obtained by reversing the 2-morphisms.
$\mathcal {X}^{2{\text {-op}}}$ for that obtained by reversing the 2-morphisms.
We also adopt the following standard notation for functors between slices of an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$:
$\mathcal {C}$:
• if
 $f \colon x \to y$ is a morphism in
$f \colon x \to y$ is a morphism in  $\mathcal {C}$, we have a functor
such that
$\mathcal {C}$, we have a functor
such that \[ f_!\colon \mathcal{C}_{/x} \rightarrow \mathcal{C}_{/y} \]
\[ f_!\colon \mathcal{C}_{/x} \rightarrow \mathcal{C}_{/y} \]
 $f_!(t \rightarrow x) = t \rightarrow x \rightarrow y$, i.e. given by composition with
$f_!(t \rightarrow x) = t \rightarrow x \rightarrow y$, i.e. given by composition with  $f$;
$f$;• if pullbacks along
 $f$ exist in
$f$ exist in  $\mathcal {C}$, then
$\mathcal {C}$, then  $f_{!}$ has a right adjoint
$f_{!}$ has a right adjoint
 \[ f^*\colon \mathcal{C}_{/y} \rightarrow \mathcal{C}_{/x}; \]
\[ f^*\colon \mathcal{C}_{/y} \rightarrow \mathcal{C}_{/x}; \]
• if
 $f^{*}$ has a further right adjoint, this will be denoted by
(this right adjoint exists for all
$f^{*}$ has a further right adjoint, this will be denoted by
(this right adjoint exists for all \[ f_* \colon \mathcal{C}_{/x} \to \mathcal{C}_{/y} \]
\[ f_* \colon \mathcal{C}_{/x} \to \mathcal{C}_{/y} \]
 $f$ precisely when
$f$ precisely when  $\mathcal {C}$ is locally cartesian closed, for example if
$\mathcal {C}$ is locally cartesian closed, for example if  $\mathcal {C}$ is an
$\mathcal {C}$ is an  $\infty$-topos).
$\infty$-topos).
2. Bispans and distributive functors
2.1  $(\infty,2)$-categories and adjunctions
$(\infty,2)$-categories and adjunctions
Throughout this paper we work with ![]() $(\infty,2)$-categories, and in this section we review some basic results we use from the theory of
$(\infty,2)$-categories, and in this section we review some basic results we use from the theory of ![]() $(\infty,2)$-categories, particularly regarding adjunctions. There are several equivalent ways to define these objects and their homotopy theory, including Rezk's
$(\infty,2)$-categories, particularly regarding adjunctions. There are several equivalent ways to define these objects and their homotopy theory, including Rezk's ![]() $\Theta _{2}$-spaces [Reference RezkRez10] and Barwick's 2-fold Segal spaces [Reference BarwickBar05]. We can also view
$\Theta _{2}$-spaces [Reference RezkRez10] and Barwick's 2-fold Segal spaces [Reference BarwickBar05]. We can also view ![]() $(\infty,2)$-categories as
$(\infty,2)$-categories as ![]() $\infty$-categories enriched in
$\infty$-categories enriched in ![]() $\infty$-categories, which can be rigidified to categories strictly enriched in quasicategories (see [Reference HaugsengHau15]); the latter is the model used in the papers of Riehl and Verity. We will not review the details of any of these constructions here, as we do not need to refer to any particular model of
$\infty$-categories, which can be rigidified to categories strictly enriched in quasicategories (see [Reference HaugsengHau15]); the latter is the model used in the papers of Riehl and Verity. We will not review the details of any of these constructions here, as we do not need to refer to any particular model of ![]() $(\infty,2)$-categories in this paper.
$(\infty,2)$-categories in this paper.
We will, however, use the Yoneda lemma for ![]() $(\infty,2)$-categories, which is a special case of Hinich's Yoneda lemma for enriched
$(\infty,2)$-categories, which is a special case of Hinich's Yoneda lemma for enriched ![]() $\infty$-categories [Reference HinichHin20].
$\infty$-categories [Reference HinichHin20].
Theorem 2.1.1 (Hinich)
For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$ there exists a fully faithful functor of
$\mathcal {X}$ there exists a fully faithful functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
such that for any functor ![]() $\Phi \colon \mathcal {X}^{{\text {op}}} \to {\text {CAT}}_{\infty }$ there is a natural equivalence of
$\Phi \colon \mathcal {X}^{{\text {op}}} \to {\text {CAT}}_{\infty }$ there is a natural equivalence of ![]() $\infty$-categories
$\infty$-categories
Remark 2.1.2 Hinich's work does use a specific model for ![]() $(\infty,2)$-categories, namely a certain definition of enriched
$(\infty,2)$-categories, namely a certain definition of enriched ![]() $\infty$-categories specialized to enrichment in
$\infty$-categories specialized to enrichment in ![]() ${\text {Cat}}_\infty$. Hinich's definition has been compared to the original one of Gepner and Haugseng [Reference Gepner and HaugsengGH15] by Macpherson [Reference MacphersonMac21], and for enrichment in
${\text {Cat}}_\infty$. Hinich's definition has been compared to the original one of Gepner and Haugseng [Reference Gepner and HaugsengGH15] by Macpherson [Reference MacphersonMac21], and for enrichment in ![]() ${\text {Cat}}_\infty$ the latter is equivalent to complete 2-fold Segal spaces [Reference HaugsengHau15], which, in turn, is known by work of Barwick and Schommer-Pries [Reference Barwick and Schommer-PriesBSP21] to be equivalent to most other approaches to
${\text {Cat}}_\infty$ the latter is equivalent to complete 2-fold Segal spaces [Reference HaugsengHau15], which, in turn, is known by work of Barwick and Schommer-Pries [Reference Barwick and Schommer-PriesBSP21] to be equivalent to most other approaches to ![]() $(\infty,2)$-categories (including the complicial sets of Verity by recent work of Gagna, Harpaz, and Lanari [Reference Gagna, Harpaz and LanariGHL22]).
$(\infty,2)$-categories (including the complicial sets of Verity by recent work of Gagna, Harpaz, and Lanari [Reference Gagna, Harpaz and LanariGHL22]).
Recall that there exists a universal adjunction. This is a ![]() $2$-category
$2$-category ![]() ${\text {ADJ}}$ with two objects
${\text {ADJ}}$ with two objects ![]() $-$ and
$-$ and ![]() $+$ and generated by
$+$ and generated by ![]() $1$-morphisms
$1$-morphisms ![]() $L \colon \Delta ^1 = \{ - \rightarrow + \} \rightarrow {\text {ADJ}}$ and
$L \colon \Delta ^1 = \{ - \rightarrow + \} \rightarrow {\text {ADJ}}$ and ![]() $R \colon \Delta ^1 = \{ + \rightarrow - \} \rightarrow {\text {ADJ}}$ such that
$R \colon \Delta ^1 = \{ + \rightarrow - \} \rightarrow {\text {ADJ}}$ such that ![]() $L$ is left adjoint to
$L$ is left adjoint to ![]() $R$; see [Reference Riehl and VerityRV16] for an explicit combinatorial definition of this 2-category. An adjunction in a 2-category can then equivalently be described as a functor from
$R$; see [Reference Riehl and VerityRV16] for an explicit combinatorial definition of this 2-category. An adjunction in a 2-category can then equivalently be described as a functor from ![]() ${\text {ADJ}}$. This universal property also holds in
${\text {ADJ}}$. This universal property also holds in ![]() $(\infty,2)$-categories, where we can formulate it more precisely as follows.
$(\infty,2)$-categories, where we can formulate it more precisely as follows.
Theorem 2.1.3 (Riehl–Verity)
Given an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$, the induced maps of spaces
$\mathcal {X}$, the induced maps of spaces
are both inclusions of components whose images are the subspaces
spanned by those functors that are left and right adjoints, respectively.
For details, see [Reference Riehl and VerityRV16, Theorems 4.3.11 and 4.4.18]. See also [Reference Harpaz, Nuiten and PrasmaHNP19] for an alternative proof, using the cotangent complex of ![]() $(\infty,2)$-categories.
$(\infty,2)$-categories.
We need to upgrade this to a statement about ![]() $(\infty,2)$-categories rather than just
$(\infty,2)$-categories rather than just ![]() $\infty$-groupoids. This follows from the next observation, which identifies the morphisms and 2-morphisms in the
$\infty$-groupoids. This follows from the next observation, which identifies the morphisms and 2-morphisms in the ![]() $(\infty,2)$-category of adjunctions using some results from [Reference HaugsengHau21]; to state this we need some terminology that will be important throughout the paper.
$(\infty,2)$-category of adjunctions using some results from [Reference HaugsengHau21]; to state this we need some terminology that will be important throughout the paper.
Definition 2.1.4 Let ![]() $\mathcal {X}$ be an
$\mathcal {X}$ be an ![]() $(\infty,2)$-category and consider a commutative square
$(\infty,2)$-category and consider a commutative square

in ![]() $\mathcal {X}$. If
$\mathcal {X}$. If ![]() $g$ and
$g$ and ![]() $g'$ are left adjoints, with corresponding right adjoints
$g'$ are left adjoints, with corresponding right adjoints ![]() $h$ and
$h$ and ![]() $h'$, then we can use the units and counits of the adjunctions to define a mate (or Beck–Chevalley) transformation
$h'$, then we can use the units and counits of the adjunctions to define a mate (or Beck–Chevalley) transformation ![]() $\xi h' \to h \eta$ as the composite
$\xi h' \to h \eta$ as the composite
We say the square is right adjointable if this mate transformation is an equivalence. Dually, if ![]() $g$ and
$g$ and ![]() $g'$ are right adjoints, with left adjoints
$g'$ are right adjoints, with left adjoints ![]() $f$ and
$f$ and ![]() $f'$, we say the square is left adjointable if the mate transformation
$f'$, we say the square is left adjointable if the mate transformation
is an equivalence.
Proposition 2.1.5 Let ![]() $\mathcal {X}$ and
$\mathcal {X}$ and ![]() $\mathcal {Y}$ be
$\mathcal {Y}$ be ![]() $(\infty,2)$-categories. A 1-morphism in the
$(\infty,2)$-categories. A 1-morphism in the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, i.e. a natural transformation
${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, i.e. a natural transformation ![]() $\eta \colon F \to G$ of functors
$\eta \colon F \to G$ of functors ![]() $F,G \colon \mathcal {X} \to \mathcal {Y}$, is a right (left) adjoint if and only if:
$F,G \colon \mathcal {X} \to \mathcal {Y}$, is a right (left) adjoint if and only if:
(1) for every object
 $x \in \mathcal {X}$, the morphism
$x \in \mathcal {X}$, the morphism  $\eta _{x} \colon F(x) \to G(x)$ is a right (left) adjoint in
$\eta _{x} \colon F(x) \to G(x)$ is a right (left) adjoint in  $\mathcal {Y}$;
$\mathcal {Y}$;(2) for every morphism
 $f \colon x \to x'$ in
$f \colon x \to x'$ in  $\mathcal {X}$, the commutative square
$\mathcal {X}$, the commutative square

is left (right) adjointable.
Proof. We consider the case of right adjoints; the left adjoint case can be proved similarly, and also follows by duality. Let ![]() ${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$ denote the
${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$ denote the ![]() $(\infty,2)$-category of functors from
$(\infty,2)$-category of functors from ![]() $\mathcal {X}$ to
$\mathcal {X}$ to ![]() $\mathcal {Y}$ with lax natural transformations as morphisms (see [Reference HaugsengHau21, § 3] for a precise definition). We can view the natural transformation
$\mathcal {Y}$ with lax natural transformations as morphisms (see [Reference HaugsengHau21, § 3] for a precise definition). We can view the natural transformation ![]() $\eta$ as a morphism in
$\eta$ as a morphism in ![]() ${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$. By [Reference HaugsengHau21, Theorem 4.6] it has a right adjoint here if and only if
${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$. By [Reference HaugsengHau21, Theorem 4.6] it has a right adjoint here if and only if ![]() $\eta _{x}$ has a right adjoint in
$\eta _{x}$ has a right adjoint in ![]() $\mathcal {Y}$ for every
$\mathcal {Y}$ for every ![]() $x \in \mathcal {X}$; this right adjoint is given on morphisms by taking mates. If
$x \in \mathcal {X}$; this right adjoint is given on morphisms by taking mates. If ![]() $\eta$ has a right adjoint
$\eta$ has a right adjoint ![]() $\rho$ in
$\rho$ in ![]() ${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, then by uniqueness this is also a right adjoint in
${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, then by uniqueness this is also a right adjoint in ![]() ${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$; hence,
${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$; hence, ![]() $\eta$ must be given objectwise by left adjoints and the naturality squares of
$\eta$ must be given objectwise by left adjoints and the naturality squares of ![]() $\rho$ are the corresponding mate squares: in particular, these mate squares must commute, so conditions (1) and (2) hold. Conversely, if these conditions hold for
$\rho$ are the corresponding mate squares: in particular, these mate squares must commute, so conditions (1) and (2) hold. Conversely, if these conditions hold for ![]() $\eta$ then
$\eta$ then ![]() $\eta$ has a right adjoint
$\eta$ has a right adjoint ![]() $\rho$ in
$\rho$ in ![]() ${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$ and the lax naturality squares of
${\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$ and the lax naturality squares of ![]() $\rho$ actually commute. By [Reference HaugsengHau21, Corollary 3.17] this means that
$\rho$ actually commute. By [Reference HaugsengHau21, Corollary 3.17] this means that ![]() $\rho$ is in the image of the canonical functor
$\rho$ is in the image of the canonical functor ![]() ${\text {FUN}}(\mathcal {X}, \mathcal {Y}) \to {\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$; moreover, this functor is locally fully faithful so the unit and counit of the adjunction also lie in
${\text {FUN}}(\mathcal {X}, \mathcal {Y}) \to {\text {FUN}}(\mathcal {X},\mathcal {Y})_{{\text {lax}}}$; moreover, this functor is locally fully faithful so the unit and counit of the adjunction also lie in ![]() ${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, and so
${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, and so ![]() $\eta$ has a right adjoint in
$\eta$ has a right adjoint in ![]() ${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, as required.
${\text {FUN}}(\mathcal {X}, \mathcal {Y})$, as required.
Notation 2.1.6 Let ![]() $\mathcal {X}$ be an
$\mathcal {X}$ be an ![]() $(\infty,2)$-category. We write
$(\infty,2)$-category. We write ![]() ${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ for the locally full sub-
${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ for the locally full sub-![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() ${\text {FUN}}(\Delta ^{1}, \mathcal {X})$ whose objects are the morphisms that are left adjoints and whose morphisms are the right adjointable squares. Similarly, we write
${\text {FUN}}(\Delta ^{1}, \mathcal {X})$ whose objects are the morphisms that are left adjoints and whose morphisms are the right adjointable squares. Similarly, we write ![]() ${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {radj}}}$ for the sub-
${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {radj}}}$ for the sub-![]() $(\infty,2)$-category of right adjoints and left adjointable squares.
$(\infty,2)$-category of right adjoints and left adjointable squares.
Corollary 2.1.7 The functors ![]() $L^{*}, R^{*} \colon {\text {FUN}}({\text {ADJ}}, \mathcal {X}) \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})$ identify the
$L^{*}, R^{*} \colon {\text {FUN}}({\text {ADJ}}, \mathcal {X}) \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})$ identify the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {FUN}}({\text {ADJ}}, \mathcal {X})$ with the sub-
${\text {FUN}}({\text {ADJ}}, \mathcal {X})$ with the sub-![]() $(\infty,2)$-categories
$(\infty,2)$-categories ![]() ${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ and
${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ and ![]() ${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {radj}}}$, respectively.
${\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {radj}}}$, respectively.
Proof. We consider the case of left adjoints; the proof for right adjoints is the same. For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {Y}$ we have the following natural commutative square:
$\mathcal {Y}$ we have the following natural commutative square:

Here Theorem 2.1.3 implies that the right vertical map is a monomorphism of ![]() $\infty$-groupoids with image the components of
$\infty$-groupoids with image the components of ![]() ${\text {Map}}(\Delta ^{1}, {\text {FUN}}(\mathcal {Y}, \mathcal {X}))$ that correspond to left adjoints in
${\text {Map}}(\Delta ^{1}, {\text {FUN}}(\mathcal {Y}, \mathcal {X}))$ that correspond to left adjoints in ![]() ${\text {FUN}}(\mathcal {Y}, \mathcal {X})$. Using Proposition 2.1.5 we can identify these as precisely those in the image of the subspace
${\text {FUN}}(\mathcal {Y}, \mathcal {X})$. Using Proposition 2.1.5 we can identify these as precisely those in the image of the subspace ![]() ${\text {Map}}(\mathcal {Y}, {\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}})$ under the bottom horizontal equivalence. By the Yoneda lemma it follows that
${\text {Map}}(\mathcal {Y}, {\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}})$ under the bottom horizontal equivalence. By the Yoneda lemma it follows that ![]() $L^{*} \colon {\text {FUN}}({\text {ADJ}}, \mathcal {X}) \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ is an equivalence.
$L^{*} \colon {\text {FUN}}({\text {ADJ}}, \mathcal {X}) \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})^{{\text {ladj}}}$ is an equivalence.
2.2 Adjointable functors and spans
In this section we introduce (left and right) adjointable functors and review the universal property of ![]() $(\infty,2)$-categories of spans in terms of these.
$(\infty,2)$-categories of spans in terms of these.
Definition 2.2.1 A span pair ![]() $(\mathcal {C},\mathcal {C}_{F})$ consists of an
$(\mathcal {C},\mathcal {C}_{F})$ consists of an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ together with a wide subcategory
$\mathcal {C}$ together with a wide subcategory ![]() $\mathcal {C}_{F}$ (i.e. one containing all objects and equivalences) such that given morphisms
$\mathcal {C}_{F}$ (i.e. one containing all objects and equivalences) such that given morphisms ![]() $x \xrightarrow {f} y$ in
$x \xrightarrow {f} y$ in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $z \xrightarrow {g} y$ in
$z \xrightarrow {g} y$ in ![]() $\mathcal {C}$, the pullback
$\mathcal {C}$, the pullback

exists in ![]() $\mathcal {C}$, and moreover
$\mathcal {C}$, and moreover ![]() $f'$ is also in
$f'$ is also in ![]() $\mathcal {C}_{F}$. If
$\mathcal {C}_{F}$. If ![]() $(\mathcal {C}, \mathcal {C}_{F})$ and
$(\mathcal {C}, \mathcal {C}_{F})$ and ![]() $(\mathcal {C}',\mathcal {C}'_{F})$ are span pairs, then a morphism of span pairs
$(\mathcal {C}',\mathcal {C}'_{F})$ are span pairs, then a morphism of span pairs ![]() $(\mathcal {C}, \mathcal {C}_{F}) \to (\mathcal {C}',\mathcal {C}'_{F})$ is a functor
$(\mathcal {C}, \mathcal {C}_{F}) \to (\mathcal {C}',\mathcal {C}'_{F})$ is a functor ![]() $\phi \colon \mathcal {C} \to \mathcal {C}'$ such that
$\phi \colon \mathcal {C} \to \mathcal {C}'$ such that ![]() $\phi (\mathcal {C}_{F}) \subseteq \mathcal {C}'_{F}$ and
$\phi (\mathcal {C}_{F}) \subseteq \mathcal {C}'_{F}$ and ![]() $\phi$ preserves pullbacks along morphisms in
$\phi$ preserves pullbacks along morphisms in ![]() $\mathcal {C}_{F}$. We write
$\mathcal {C}_{F}$. We write ![]() ${\text {Pair}}$ for the
${\text {Pair}}$ for the ![]() $\infty$-category of span pairs, which can be defined as a subcategory of
$\infty$-category of span pairs, which can be defined as a subcategory of ![]() ${\text {Fun}}(\Delta ^{1}, {\text {Cat}}_\infty )$.
${\text {Fun}}(\Delta ^{1}, {\text {Cat}}_\infty )$.
Given a span pair ![]() $(\mathcal {C}, \mathcal {C}_{F})$ we can, as in [Reference BarwickBar17, § 3], define an
$(\mathcal {C}, \mathcal {C}_{F})$ we can, as in [Reference BarwickBar17, § 3], define an ![]() $\infty$-category
$\infty$-category ![]() $\operatorname {Span}_{F}(\mathcal {C})$ whose objects are the objects of
$\operatorname {Span}_{F}(\mathcal {C})$ whose objects are the objects of ![]() $\mathcal {C}$, with morphisms from
$\mathcal {C}$, with morphisms from ![]() $x$ to
$x$ to ![]() $y$ given by spans
$y$ given by spans

where ![]() $f$ is in
$f$ is in ![]() $\mathcal {C}_{F}$; we compose spans by taking pullbacks. Following [Reference HaugsengHau18, § 5] we can upgrade this to an
$\mathcal {C}_{F}$; we compose spans by taking pullbacks. Following [Reference HaugsengHau18, § 5] we can upgrade this to an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ whose 2-morphisms are morphisms of spans, i.e. diagrams
$\operatorname {SPAN}_{F}(\mathcal {C})$ whose 2-morphisms are morphisms of spans, i.e. diagrams

in ![]() $\mathcal {C}$, where
$\mathcal {C}$, where ![]() $z \to z'$ can be any morphism in
$z \to z'$ can be any morphism in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Warning 2.2.2 In [Reference HaugsengHau18], the ![]() $(\infty,2)$-category of spans in
$(\infty,2)$-category of spans in ![]() $\mathcal {C}$ was denoted
$\mathcal {C}$ was denoted ![]() $\operatorname {Span}_{1}^{+}(\mathcal {C})$, while
$\operatorname {Span}_{1}^{+}(\mathcal {C})$, while ![]() $\operatorname {SPAN}_{n}(\mathcal {C})$ was used for an
$\operatorname {SPAN}_{n}(\mathcal {C})$ was used for an ![]() $n$-uple
$n$-uple ![]() $\infty$-category of spans.
$\infty$-category of spans.
Remark 2.2.3 In the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$, every morphism of the form
$\operatorname {SPAN}_{F}(\mathcal {C})$, every morphism of the form
with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$ has a left adjoint, namely the reversed span
$\mathcal {C}_{F}$ has a left adjoint, namely the reversed span
The counit is the 2-morphism

and the unit is

where the fibre product ![]() $x \times _{y}x$ is over two copies of
$x \times _{y}x$ is over two copies of ![]() $f$ and
$f$ and ![]() $\Delta$ is the corresponding diagonal.
$\Delta$ is the corresponding diagonal.
The ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ enjoys a universal property: roughly speaking, it is obtained from
$\operatorname {SPAN}_{F}(\mathcal {C})$ enjoys a universal property: roughly speaking, it is obtained from ![]() $\mathcal {C}^{{\text {op}}}$ by freely adding left adjoints for morphisms in
$\mathcal {C}^{{\text {op}}}$ by freely adding left adjoints for morphisms in ![]() $(\mathcal {C}_{F})^{{\text {op}}}$. To state this more precisely, we need some definitions.
$(\mathcal {C}_{F})^{{\text {op}}}$. To state this more precisely, we need some definitions.
Definition 2.2.4 Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and
$(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and ![]() $\mathcal {X}$ an
$\mathcal {X}$ an ![]() $(\infty,2)$-category. A functor
$(\infty,2)$-category. A functor ![]() $\Phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is left
$\Phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is left ![]() $F$-preadjointable if for every morphism
$F$-preadjointable if for every morphism ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$ the 1-morphism
$\mathcal {C}_{F}$ the 1-morphism ![]() $f^{\circledast } := \Phi (f) \colon \Phi (y) \to \Phi (x)$ in
$f^{\circledast } := \Phi (f) \colon \Phi (y) \to \Phi (x)$ in ![]() $\mathcal {X}$ has a left adjoint
$\mathcal {X}$ has a left adjoint ![]() $f_{\oplus }$ in
$f_{\oplus }$ in ![]() $\mathcal {X}$.
$\mathcal {X}$.
Definition 2.2.5 We say that ![]() $\Phi$ is left
$\Phi$ is left ![]() $F$-adjointable if it is left
$F$-adjointable if it is left ![]() $F$-preadjointable and for every cartesian square
$F$-preadjointable and for every cartesian square

in ![]() $\mathcal {C}$ with
$\mathcal {C}$ with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$, the commutative square
$\mathcal {C}_{F}$, the commutative square

in ![]() $\mathcal {X}$ is left adjointable. We write
$\mathcal {X}$ is left adjointable. We write ![]() ${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ for the subspace of
${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ for the subspace of ![]() ${\text {Map}}(\mathcal {C}^{{\text {op}}},\mathcal {X})$ whose components are the left
${\text {Map}}(\mathcal {C}^{{\text {op}}},\mathcal {X})$ whose components are the left ![]() $F$-adjointable functors.
$F$-adjointable functors.
Remark 2.2.6 In other words, ![]() $\Phi$ is left
$\Phi$ is left ![]() $F$-adjointable if for every cartesian square (11) with
$F$-adjointable if for every cartesian square (11) with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$, the Beck–Chevalley transformation
$\mathcal {C}_{F}$, the Beck–Chevalley transformation
is an equivalence.
Theorem 2.2.7 (Gaitsgory and Rozenblyum [Reference Gaitsgory and RozenblyumGR17], Macpherson [Reference MacphersonMac22])
Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span pair, and let
$(\mathcal {C}, \mathcal {C}_{F})$ be a span pair, and let ![]() $\mathcal {X}$ be an
$\mathcal {X}$ be an ![]() $(\infty,2)$-category. The inclusion of the backwards maps
$(\infty,2)$-category. The inclusion of the backwards maps ![]() $\mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives a monomorphism of
$\mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives a monomorphism of ![]() $\infty$-groupoids
$\infty$-groupoids
with image ![]() ${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}},\mathcal {X})$.
${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}},\mathcal {X})$.
Remark 2.2.8 In [Reference Gaitsgory and RozenblyumGR17], Gaitsgory and Rozenblyum make use of this universal property of spans in order to encode the functoriality of various ![]() $\infty$-categories of coherent sheaves on derived schemes. They also sketch a proof of Theorem 2.2.7 using a particular construction of
$\infty$-categories of coherent sheaves on derived schemes. They also sketch a proof of Theorem 2.2.7 using a particular construction of ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$. Macpherson [Reference MacphersonMac22] has recently given an alternative, model-independent (and complete) proof. Roughly speaking, Macpherson's approach is to first show there exists an
$\operatorname {SPAN}_{F}(\mathcal {C})$. Macpherson [Reference MacphersonMac22] has recently given an alternative, model-independent (and complete) proof. Roughly speaking, Macpherson's approach is to first show there exists an ![]() $(\infty,2)$-category that represents left adjointable functors and then use the universal property to prove that this representing object has the expected description in terms of spans. The universal property has also been extended to higher categories of iterated spans by Stefanich [Reference StefanichSte20].
$(\infty,2)$-category that represents left adjointable functors and then use the universal property to prove that this representing object has the expected description in terms of spans. The universal property has also been extended to higher categories of iterated spans by Stefanich [Reference StefanichSte20].
Variant 2.2.9 If ![]() $\mathcal {X}$ is an
$\mathcal {X}$ is an ![]() $(\infty,2)$-category, then we have an equivalence of underlying
$(\infty,2)$-category, then we have an equivalence of underlying ![]() $\infty$-categories
$\infty$-categories
while a 1-morphism in ![]() $\mathcal {X}$ is a right adjoint if and only if it is a left adjoint in
$\mathcal {X}$ is a right adjoint if and only if it is a left adjoint in ![]() $\mathcal {X}^{2{\text {-op}}}$. We therefore say that a functor
$\mathcal {X}^{2{\text {-op}}}$. We therefore say that a functor ![]() $\Phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is right
$\Phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is right ![]() $F$-adjointable if the 2-opposite functor
$F$-adjointable if the 2-opposite functor
is left ![]() $F$-adjointable. Theorem 2.2.7 then tells us that the right
$F$-adjointable. Theorem 2.2.7 then tells us that the right ![]() $F$-adjointable functors correspond to functors
$F$-adjointable functors correspond to functors ![]() $\operatorname {SPAN}_{F}(\mathcal {C})^{2{\text {-op}}} \to \mathcal {X}$.
$\operatorname {SPAN}_{F}(\mathcal {C})^{2{\text {-op}}} \to \mathcal {X}$.
Variant 2.2.10 We say a functor ![]() $\Phi \colon \mathcal {C} \to \mathcal {X}$ is right
$\Phi \colon \mathcal {C} \to \mathcal {X}$ is right ![]() $F$-coadjointable if the 1-opposite functor
$F$-coadjointable if the 1-opposite functor
is left ![]() $F$-adjointable. Theorem 2.2.7 then tells us that the right
$F$-adjointable. Theorem 2.2.7 then tells us that the right ![]() $F$-coadjointable functors correspond to functors
$F$-coadjointable functors correspond to functors ![]() $\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}}} \to \mathcal {X}$. We can also combine both variants, and say that
$\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}}} \to \mathcal {X}$. We can also combine both variants, and say that ![]() $\Phi \colon \mathcal {C} \to \mathcal {X}$ is left
$\Phi \colon \mathcal {C} \to \mathcal {X}$ is left ![]() $F$-coadjointable if
$F$-coadjointable if
is left ![]() $F$-adjointable. The left
$F$-adjointable. The left ![]() $F$-coadjointable functors then correspond to functors
$F$-coadjointable functors then correspond to functors ![]() $\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}},2{\text {-op}}} \to \mathcal {X}$.
$\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}},2{\text {-op}}} \to \mathcal {X}$.
Remark 2.2.11 Unpacking the definition, and recalling that reversing the 1-morphisms in an ![]() $(\infty,2)$-category swaps left and right adjoints, we see that a functor
$(\infty,2)$-category swaps left and right adjoints, we see that a functor ![]() $\Phi \colon \mathcal {C} \to \mathcal {X}$ is right
$\Phi \colon \mathcal {C} \to \mathcal {X}$ is right ![]() $F$-coadjointable if for every morphism
$F$-coadjointable if for every morphism ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$ the 1-morphism
$\mathcal {C}_{F}$ the 1-morphism ![]() $f_{\circledast } := \Phi (f) \colon \Phi (x) \to \Phi (y)$ in
$f_{\circledast } := \Phi (f) \colon \Phi (x) \to \Phi (y)$ in ![]() $\mathcal {X}$ has a right adjoint
$\mathcal {X}$ has a right adjoint ![]() $f^{\oplus }$, and for every pullback square (11) the square
$f^{\oplus }$, and for every pullback square (11) the square

is right adjointable. Note that this is not the same as ![]() $\Phi$ being right
$\Phi$ being right ![]() $F$-adjointable in the previous sense: this condition would involve adjointability for pushout squares in
$F$-adjointable in the previous sense: this condition would involve adjointability for pushout squares in ![]() $\mathcal {C}$; indeed, to even be defined this condition would require
$\mathcal {C}$; indeed, to even be defined this condition would require ![]() $(\mathcal {C}^{{\text {op}}},\mathcal {C}^{{\text {op}}}_{F})$ to be a span pair, which may well not be the case.
$(\mathcal {C}^{{\text {op}}},\mathcal {C}^{{\text {op}}}_{F})$ to be a span pair, which may well not be the case.
2.3 The  $(\infty,2)$-category of spans
$(\infty,2)$-category of spans
For the sake of completeness, in this subsection we include a proof of Theorem 2.2.7. However, our argument is at most a minor variation of the proof of Macpherson [Reference MacphersonMac22] and we make no claims to originality. We start by observing that the presentability of ![]() ${\text {Cat}}_{(\infty,2)}$ implies that left
${\text {Cat}}_{(\infty,2)}$ implies that left ![]() $F$-adjointable functors are corepresented by some
$F$-adjointable functors are corepresented by some ![]() $(\infty,2)$-category.
$(\infty,2)$-category.
Proposition 2.3.1 Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span pair, with
$(\mathcal {C}, \mathcal {C}_{F})$ be a span pair, with ![]() $\mathcal {C}$ a small
$\mathcal {C}$ a small ![]() $\infty$-category. Then the functor
$\infty$-category. Then the functor
is corepresentable by a small ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$, so that there is a natural equivalence
$\operatorname {SPAN}_{F}(\mathcal {C})$, so that there is a natural equivalence
for any ![]() $\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$.
$\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$.
Proof. The ![]() $\infty$-category
$\infty$-category ![]() ${\text {Cat}}_{(\infty,2)}$ is presentable, for instance because it can be described as presheaves on
${\text {Cat}}_{(\infty,2)}$ is presentable, for instance because it can be described as presheaves on ![]() $\Theta _{2}$ satisfying Segal and completeness conditions, which gives an explicit presentation as an accessible localization of an
$\Theta _{2}$ satisfying Segal and completeness conditions, which gives an explicit presentation as an accessible localization of an ![]() $\infty$-category of presheaves. To prove that a copresheaf on
$\infty$-category of presheaves. To prove that a copresheaf on ![]() ${\text {Cat}}_{(\infty,2)}$ is corepresentable it therefore suffices by [Reference LurieLur09, Proposition 5.5.2.7] to show that it is accessible and preserves limits.
${\text {Cat}}_{(\infty,2)}$ is corepresentable it therefore suffices by [Reference LurieLur09, Proposition 5.5.2.7] to show that it is accessible and preserves limits.
We first show that this holds for the copresheaf ![]() ${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, -)$ of left
${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, -)$ of left ![]() $F$-preadjointable functors. By definition, a functor
$F$-preadjointable functors. By definition, a functor ![]() $\mathcal {C} \to \mathcal {X}$ is left
$\mathcal {C} \to \mathcal {X}$ is left ![]() $F$-preadjointable if it takes every morphism in
$F$-preadjointable if it takes every morphism in ![]() $\mathcal {X}$ to a left adjoint in
$\mathcal {X}$ to a left adjoint in ![]() $\mathcal {X}$. We can therefore write
$\mathcal {X}$. We can therefore write ![]() ${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ as the pullback
${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ as the pullback

where the product is over the set ![]() $S$ of equivalence classes of morphisms in
$S$ of equivalence classes of morphisms in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $R \colon \Delta ^{1} \to {\text {ADJ}}$ is the inclusion of the right adjoint of the universal adjunction. From this description, it is immediate that
$R \colon \Delta ^{1} \to {\text {ADJ}}$ is the inclusion of the right adjoint of the universal adjunction. From this description, it is immediate that ![]() ${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ preserves limits in
${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ preserves limits in ![]() $\mathcal {X}$, since this is clear for the other three corners of the square. Moreover, since
$\mathcal {X}$, since this is clear for the other three corners of the square. Moreover, since ![]() ${\text {Cat}}_{(\infty,2)}$ is presentable we can choose a regular cardinal
${\text {Cat}}_{(\infty,2)}$ is presentable we can choose a regular cardinal ![]() $\kappa$ such that
$\kappa$ such that ![]() $S$ is
$S$ is ![]() $\kappa$-small and the objects
$\kappa$-small and the objects ![]() $\mathcal {C}^{{\text {op}}}$,
$\mathcal {C}^{{\text {op}}}$, ![]() ${\text {ADJ}}$, and
${\text {ADJ}}$, and ![]() $\Delta ^{1}$ are all
$\Delta ^{1}$ are all ![]() $\kappa$-compact in
$\kappa$-compact in ![]() ${\text {Cat}}_{(\infty,2)}$. Then we see that
${\text {Cat}}_{(\infty,2)}$. Then we see that ![]() ${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}},-)$ preserves
${\text {Map}}_{F{\text {-lpreadj}}}(\mathcal {C}^{{\text {op}}},-)$ preserves ![]() $\kappa$-filtered colimits, since the other corners of the pullback square do so (as
$\kappa$-filtered colimits, since the other corners of the pullback square do so (as ![]() $\kappa$-filtered colimits in
$\kappa$-filtered colimits in ![]() $\mathcal {S}$ commute with
$\mathcal {S}$ commute with ![]() $\kappa$-small limits, such as our product over
$\kappa$-small limits, such as our product over ![]() $S$).
$S$).
For ![]() ${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ we impose the additional requirement that every cartesian square (11) in
${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ we impose the additional requirement that every cartesian square (11) in ![]() $\mathcal {C}$ where the horizontal maps are in
$\mathcal {C}$ where the horizontal maps are in ![]() $\mathcal {C}_{F}$ is taken to a left adjointable square in
$\mathcal {C}_{F}$ is taken to a left adjointable square in ![]() $\mathcal {X}$. By Proposition 2.1.5 the left adjointable squares are the right adjoints in
$\mathcal {X}$. By Proposition 2.1.5 the left adjointable squares are the right adjoints in ![]() $\mathcal {X}^{\Delta ^{1}}$, so if
$\mathcal {X}^{\Delta ^{1}}$, so if ![]() $S'$ denotes the set of equivalence classes of relevant cartesian squares in
$S'$ denotes the set of equivalence classes of relevant cartesian squares in ![]() $\mathcal {C}$, we can write
$\mathcal {C}$, we can write ![]() ${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ as the following pullback:
${\text {Map}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ as the following pullback:

The same argument as for left ![]() $F$-preadjointable maps now implies that the presheaf
$F$-preadjointable maps now implies that the presheaf ![]() ${\text {Map}}_{F{\text {-radj}}}(\mathcal {C}, -)$ is also accessible and preserves limits and, hence, is corepresentable.
${\text {Map}}_{F{\text {-radj}}}(\mathcal {C}, -)$ is also accessible and preserves limits and, hence, is corepresentable.
Remark 2.3.2 The identity of ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ corresponds under (13) to a left
$\operatorname {SPAN}_{F}(\mathcal {C})$ corresponds under (13) to a left ![]() $F$-adjointable functor
$F$-adjointable functor
such that the equivalence (13) arises by restriction along ![]() $i$.
$i$.
Remark 2.3.3 From the universal property we immediately obtain a functor from span pairs to ![]() $(\infty,2)$-categories: for any
$(\infty,2)$-categories: for any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$, composition with a morphism of span pairs
$\mathcal {X}$, composition with a morphism of span pairs ![]() $\phi \colon (\mathcal {C}, \mathcal {C}_{F}) \to (\mathcal {C}', \mathcal {C}'_{F'})$ restricts to a morphism
$\phi \colon (\mathcal {C}, \mathcal {C}_{F}) \to (\mathcal {C}', \mathcal {C}'_{F'})$ restricts to a morphism
natural in ![]() $\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$. We obtain a functor
$\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$. We obtain a functor
Proposition 2.3.1 says that the corresponding functor ![]() ${\text {Pair}}^{{\text {op}}} \to {\text {Fun}}({\text {Cat}}_{(\infty,2)}, \mathcal {S})$ takes values in corepresentable copresheaves, and so by the Yoneda lemma factors through a canonical functor
${\text {Pair}}^{{\text {op}}} \to {\text {Fun}}({\text {Cat}}_{(\infty,2)}, \mathcal {S})$ takes values in corepresentable copresheaves, and so by the Yoneda lemma factors through a canonical functor ![]() $\operatorname {SPAN} \colon {\text {Pair}} \to {\text {Cat}}_{(\infty,2)}$.
$\operatorname {SPAN} \colon {\text {Pair}} \to {\text {Cat}}_{(\infty,2)}$.
We can upgrade the equivalence of Proposition 2.3.1 to a statement at the level of ![]() $(\infty,2)$-categories, rather than just
$(\infty,2)$-categories, rather than just ![]() $\infty$-groupoids. To state this we first need some notation.
$\infty$-groupoids. To state this we first need some notation.
Definition 2.3.4 Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and
$(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and ![]() $\mathcal {X}$ an
$\mathcal {X}$ an ![]() $(\infty,2)$-category. We say that a natural transformation
$(\infty,2)$-category. We say that a natural transformation ![]() $\eta \colon \mathcal {C}^{{\text {op}}} \times \Delta ^{1} \to \mathcal {X}$ is left
$\eta \colon \mathcal {C}^{{\text {op}}} \times \Delta ^{1} \to \mathcal {X}$ is left ![]() $F$-adjointable if it corresponds to a left
$F$-adjointable if it corresponds to a left ![]() $F$-adjointable functor
$F$-adjointable functor ![]() $\mathcal {C}^{{\text {op}}} \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})$. From Proposition 2.1.5 it follows that
$\mathcal {C}^{{\text {op}}} \to {\text {FUN}}(\Delta ^{1}, \mathcal {X})$. From Proposition 2.1.5 it follows that ![]() $\eta$ is left
$\eta$ is left ![]() $F$-adjointable if and only if the components
$F$-adjointable if and only if the components ![]() $\eta _{0},\eta _{1}$ are both left
$\eta _{0},\eta _{1}$ are both left ![]() $F$-adjointable, and for every morphism
$F$-adjointable, and for every morphism ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$, the following naturality square is left adjointable.
$\mathcal {C}_{F}$, the following naturality square is left adjointable.

Let ![]() ${\text {Fun}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ denote the subcategory of
${\text {Fun}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ denote the subcategory of ![]() ${\text {Fun}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ whose objects are the left
${\text {Fun}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ whose objects are the left ![]() $F$-adjointable functors and whose morphisms are the left
$F$-adjointable functors and whose morphisms are the left ![]() $F$-adjointable transformations. From Proposition 2.1.5 we also know that a morphism
$F$-adjointable transformations. From Proposition 2.1.5 we also know that a morphism ![]() $\mathcal {C} \times \mathsf {C}_{2} \to \mathcal {X}$ (where
$\mathcal {C} \times \mathsf {C}_{2} \to \mathcal {X}$ (where ![]() $\mathsf {C}_{2}$ is the 2-cell) corresponds to a left
$\mathsf {C}_{2}$ is the 2-cell) corresponds to a left ![]() $F$-adjointable morphism
$F$-adjointable morphism ![]() $\mathcal {C} \to {\text {FUN}}(\mathsf {C}_{2}, \mathcal {X})$ if and only if the component functors and natural transformations are left
$\mathcal {C} \to {\text {FUN}}(\mathsf {C}_{2}, \mathcal {X})$ if and only if the component functors and natural transformations are left ![]() $F$-adjointable. We therefore write
$F$-adjointable. We therefore write ![]() ${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ for the locally full sub-
${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ for the locally full sub-![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() ${\text {FUN}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ whose underlying
${\text {FUN}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ whose underlying ![]() $\infty$-category is
$\infty$-category is ![]() ${\text {Fun}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$.
${\text {Fun}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$.
Corollary 2.3.5 Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and
$(\mathcal {C}, \mathcal {C}_{F})$ be a span pair and ![]() $\mathcal {X}$ an
$\mathcal {X}$ an ![]() $(\infty,2)$-category. Composition with
$(\infty,2)$-category. Composition with ![]() $i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives an equivalence of
$i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives an equivalence of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
Proof. For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {Y}$ we have a natural equivalence
$\mathcal {Y}$ we have a natural equivalence
 \begin{align*} {\text {Map}}(\mathcal{Y}, {\text {FUN}}(\operatorname{SPAN}_{F}(\mathcal{C}), \mathcal{X})) & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}), {\text {FUN}}(\mathcal{Y}, \mathcal{X})) \\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}(\mathcal{Y}, \mathcal{X})) \\ & \simeq {\text {Map}}(\mathcal{Y}, {\text {FUN}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, \mathcal{X})), \end{align*}
\begin{align*} {\text {Map}}(\mathcal{Y}, {\text {FUN}}(\operatorname{SPAN}_{F}(\mathcal{C}), \mathcal{X})) & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}), {\text {FUN}}(\mathcal{Y}, \mathcal{X})) \\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}(\mathcal{Y}, \mathcal{X})) \\ & \simeq {\text {Map}}(\mathcal{Y}, {\text {FUN}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, \mathcal{X})), \end{align*}
where the last equivalence follows from the description of adjoints in functor ![]() $(\infty,2)$-categories in Proposition 2.1.5.
$(\infty,2)$-categories in Proposition 2.1.5.
Variant 2.3.6 Using analogous notation for right ![]() $F$-coadjointable functors, we have a natural equivalence
$F$-coadjointable functors, we have a natural equivalence
As a first step toward getting a handle on the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ we have the following observation.
$\operatorname {SPAN}_{F}(\mathcal {C})$ we have the following observation.
Lemma 2.3.7 The functor ![]() $i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ (corresponding to the identity under (13)) is essentially surjective.
$i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ (corresponding to the identity under (13)) is essentially surjective.
Proof. Let ![]() $\mathcal {I}$ denote the full sub-
$\mathcal {I}$ denote the full sub-![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ spanned by the objects in the image of
$\operatorname {SPAN}_{F}(\mathcal {C})$ spanned by the objects in the image of ![]() $i$. Then
$i$. Then ![]() $i$ factors through
$i$ factors through ![]() $i' \colon \mathcal {C}^{{\text {op}}} \to \mathcal {I}$, and
$i' \colon \mathcal {C}^{{\text {op}}} \to \mathcal {I}$, and ![]() $i'$ is again left
$i'$ is again left ![]() $F$-adjointable (since the relevant adjoints and 2-morphisms all live in
$F$-adjointable (since the relevant adjoints and 2-morphisms all live in ![]() $\mathcal {I}$). Hence,
$\mathcal {I}$). Hence, ![]() $i'$ corresponds to a functor
$i'$ corresponds to a functor ![]() $\operatorname {SPAN}_{F}(\mathcal {C}) \to \mathcal {I}$ such that the composite
$\operatorname {SPAN}_{F}(\mathcal {C}) \to \mathcal {I}$ such that the composite
is the identity. It follows that the inclusion of ![]() $\mathcal {I}$ must be essentially surjective, which means that
$\mathcal {I}$ must be essentially surjective, which means that ![]() $i$ is also essentially surjective.
$i$ is also essentially surjective.
To get a handle on the ![]() $\infty$-categories of morphisms in
$\infty$-categories of morphisms in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$, we will use two further ingredients: (1) the Yoneda Lemma for
$\operatorname {SPAN}_{F}(\mathcal {C})$, we will use two further ingredients: (1) the Yoneda Lemma for ![]() $(\infty,2)$-categories (Theorem 2.1.1) due to Hinich; and (2) the construction of the free (co)cartesian fibrations due to Gepner, Nikolaus, and the second author [Reference Gepner, Haugseng and NikolausGHN17]. Applying the Yoneda lemma to
$(\infty,2)$-categories (Theorem 2.1.1) due to Hinich; and (2) the construction of the free (co)cartesian fibrations due to Gepner, Nikolaus, and the second author [Reference Gepner, Haugseng and NikolausGHN17]. Applying the Yoneda lemma to ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ we get a canonical family of left
$\operatorname {SPAN}_{F}(\mathcal {C})$ we get a canonical family of left ![]() $F$-adjointable functors to
$F$-adjointable functors to ![]() ${\text {CAT}}_{\infty }$.
${\text {CAT}}_{\infty }$.
Proposition 2.3.8 There is a left ![]() $F$-adjointable functor
$F$-adjointable functor
such that for any right ![]() $F$-coadjointable functor (in the sense of Variant 2.2.10)
$F$-coadjointable functor (in the sense of Variant 2.2.10) ![]() $\Phi \colon \mathcal {C} \to {\text {CAT}}_{\infty }$ there is a natural equivalence
$\Phi \colon \mathcal {C} \to {\text {CAT}}_{\infty }$ there is a natural equivalence
where the latter denotes the ![]() $\infty$-category of right
$\infty$-category of right ![]() $F$-coadjointable natural transformations.
$F$-coadjointable natural transformations.
Proof. Applying Hinich's Yoneda embedding (Theorem 2.1.1) to ![]() $\operatorname {SPAN}_{F,L}(\mathcal {C})$ we get a functor
$\operatorname {SPAN}_{F,L}(\mathcal {C})$ we get a functor
By Proposition 2.3.1 this corresponds to a left ![]() $F$-adjointable functor
$F$-adjointable functor
via the equivalence of Variant 2.3.6. Translating the universal property of representable presheaves through the latter equivalence now gives the result.
To proceed further, we will work unstraightened, i.e. with the cocartesian fibrations corresponding to ![]() $\mathsf {Y}(c) \colon \mathcal {C} \to {\text {Cat}}_\infty$.
$\mathsf {Y}(c) \colon \mathcal {C} \to {\text {Cat}}_\infty$.
Lemma 2.3.9 The straightening equivalence
identifies the subcategory ![]() ${\text {Fun}}_{F{\text {-rcoadj}}}(\mathcal {C}, {\text {CAT}}_{\infty })$ with a full subcategory
${\text {Fun}}_{F{\text {-rcoadj}}}(\mathcal {C}, {\text {CAT}}_{\infty })$ with a full subcategory
where the right-hand side is the ![]() $\infty$-category of cocartesian fibrations over
$\infty$-category of cocartesian fibrations over ![]() $\mathcal {C}$ that have cartesian morphisms over
$\mathcal {C}$ that have cartesian morphisms over ![]() $\mathcal {C}_{F}$, and whose morphisms are functors over
$\mathcal {C}_{F}$, and whose morphisms are functors over ![]() $\mathcal {C}$ that preserve cocartesian morphisms as well as cartesian morphisms over
$\mathcal {C}$ that preserve cocartesian morphisms as well as cartesian morphisms over ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
Proof. By [Reference LurieLur09, Corollary 5.2.2.4] a cocartesian fibration to ![]() $\mathcal {C}$ has cartesian morphisms over
$\mathcal {C}$ has cartesian morphisms over ![]() $\mathcal {C}_{F}$ if and only if it has locally cartesian morphisms over
$\mathcal {C}_{F}$ if and only if it has locally cartesian morphisms over ![]() $\mathcal {C}_{F}$, which is equivalent to the corresponding morphisms in
$\mathcal {C}_{F}$, which is equivalent to the corresponding morphisms in ![]() ${\text {Cat}}_\infty$ having right adjoints (cf. [Reference LurieLur09, Definition 5.2.2.1]). Thus, the unstraightening of a right
${\text {Cat}}_\infty$ having right adjoints (cf. [Reference LurieLur09, Definition 5.2.2.1]). Thus, the unstraightening of a right ![]() $F$-coadjointable functor gives an object of
$F$-coadjointable functor gives an object of ![]() ${\text {Cat}}_{\infty /\mathcal {C}}^{{\text {cocart}}+F{\text {-cart}}}$. Moreover, by [Reference LurieLur17, Proposition 4.7.4.17] a morphism over
${\text {Cat}}_{\infty /\mathcal {C}}^{{\text {cocart}}+F{\text {-cart}}}$. Moreover, by [Reference LurieLur17, Proposition 4.7.4.17] a morphism over ![]() $\mathcal {C}$ that preserves cocartesian morphisms and cartesian morphisms over
$\mathcal {C}$ that preserves cocartesian morphisms and cartesian morphisms over ![]() $\mathcal {C}_{F}$ corresponds to a natural transformation whose naturality squares over
$\mathcal {C}_{F}$ corresponds to a natural transformation whose naturality squares over ![]() $\mathcal {C}_{F}$ are right adjointable, which is precisely the requirement for coadjointable natural transformations.
$\mathcal {C}_{F}$ are right adjointable, which is precisely the requirement for coadjointable natural transformations.
Definition 2.3.10 For ![]() $c \in \mathcal {C}$, let
$c \in \mathcal {C}$, let ![]() $\mathcal {Y}_{c} \to \mathcal {C}$ denote the cocartesian fibration classified by the right
$\mathcal {Y}_{c} \to \mathcal {C}$ denote the cocartesian fibration classified by the right ![]() $F$-coadjointable functor
$F$-coadjointable functor ![]() $\mathsf {Y}(c) \colon \mathcal {C} \rightarrow {\text {Cat}}_\infty$ that corresponds via Proposition 2.3.8 to the functor
$\mathsf {Y}(c) \colon \mathcal {C} \rightarrow {\text {Cat}}_\infty$ that corresponds via Proposition 2.3.8 to the functor ![]() $\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}}} \to {\text {CAT}}_{\infty }$ represented by
$\operatorname {SPAN}_{F}(\mathcal {C})^{{\text {op}}} \to {\text {CAT}}_{\infty }$ represented by ![]() $i(c)$.
$i(c)$.
The idea is now to construct a ‘candidate’ for ![]() $\mathcal {Y}_{c}$ using a result from [Reference Gepner, Haugseng and NikolausGHN17] together with the following observation.
$\mathcal {Y}_{c}$ using a result from [Reference Gepner, Haugseng and NikolausGHN17] together with the following observation.
Lemma 2.3.11 If ![]() $p \colon \mathcal {E} \to \mathcal {C}$ is a functor such that
$p \colon \mathcal {E} \to \mathcal {C}$ is a functor such that ![]() $\mathcal {E}$ has
$\mathcal {E}$ has ![]() $p$-cartesian morphisms over morphisms in
$p$-cartesian morphisms over morphisms in ![]() $\mathcal {C}_{F}$, then the functor
$\mathcal {C}_{F}$, then the functor
given by restriction along the inclusion
is an equivalence, where ![]() $\mathcal {C}_{/x}^{F}$ denotes the full subcategory of
$\mathcal {C}_{/x}^{F}$ denotes the full subcategory of ![]() $\mathcal {C}_{/x}$ spanned by morphisms to
$\mathcal {C}_{/x}$ spanned by morphisms to ![]() $x$ in
$x$ in ![]() $\mathcal {C}_{F}$, and
$\mathcal {C}_{F}$, and ![]() ${\text {Fun}}_{/\mathcal {C}}^{F{\text {-cart}}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$ is the full subcategory of
${\text {Fun}}_{/\mathcal {C}}^{F{\text {-cart}}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$ is the full subcategory of ![]() ${\text {Fun}}_{/\mathcal {C}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$ spanned by functors that preserve cartesian morphisms over
${\text {Fun}}_{/\mathcal {C}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$ spanned by functors that preserve cartesian morphisms over ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
Proof. We use the results on relative Kan extensions from [Reference LurieLur09, § 4.3.2]. For every object ![]() $f \colon y \to x$ of
$f \colon y \to x$ of ![]() $\mathcal {C}_{/x}^{F}$ the
$\mathcal {C}_{/x}^{F}$ the ![]() $\infty$-category
$\infty$-category
is contractible, since ![]() ${\text {id}}_{x}$ is a terminal object in
${\text {id}}_{x}$ is a terminal object in ![]() $\mathcal {C}^{F}_{/x}$. Hence, a morphism
$\mathcal {C}^{F}_{/x}$. Hence, a morphism
is a ![]() $p$-limit if and only if it's a cartesian morphism by [Reference LurieLur09, Example 4.3.1.4]. It follows that a functor
$p$-limit if and only if it's a cartesian morphism by [Reference LurieLur09, Example 4.3.1.4]. It follows that a functor ![]() $\Phi \colon \mathcal {C}_{/x}^{F} \to \mathcal {E}$ over
$\Phi \colon \mathcal {C}_{/x}^{F} \to \mathcal {E}$ over ![]() $\mathcal {C}$ is a
$\mathcal {C}$ is a ![]() $p$-right Kan extension from
$p$-right Kan extension from ![]() $\{x\}$ if and only if for every
$\{x\}$ if and only if for every ![]() $f \colon y \to x$ in
$f \colon y \to x$ in ![]() $\mathcal {C}_{F}$ it takes the unique morphism
$\mathcal {C}_{F}$ it takes the unique morphism ![]() $f \to {\text {id}}_{x}$ (which is cartesian over
$f \to {\text {id}}_{x}$ (which is cartesian over ![]() $f$) to a cartesian morphism in
$f$) to a cartesian morphism in ![]() $\mathcal {E}$. By the 3-for-2 property of cartesian morphisms this is equivalent to
$\mathcal {E}$. By the 3-for-2 property of cartesian morphisms this is equivalent to ![]() $\Phi$ preserving cartesian morphisms over
$\Phi$ preserving cartesian morphisms over ![]() $\mathcal {C}_{F}$. Hence, [Reference LurieLur09, Proposition 4.3.2.15] implies that, since
$\mathcal {C}_{F}$. Hence, [Reference LurieLur09, Proposition 4.3.2.15] implies that, since ![]() $\mathcal {E}$ has
$\mathcal {E}$ has ![]() $p$-cartesian morphisms over
$p$-cartesian morphisms over ![]() $\mathcal {C}_{F}$, the functor
$\mathcal {C}_{F}$, the functor ![]() ${\text {Fun}}_{/\mathcal {C}}(\mathcal {C}_{/x}^{F}, \mathcal {E}) \to {\text {Fun}}_{/\mathcal {C}}(\{x\}, \mathcal {E})$ restricts to an equivalence from the full subcategory
${\text {Fun}}_{/\mathcal {C}}(\mathcal {C}_{/x}^{F}, \mathcal {E}) \to {\text {Fun}}_{/\mathcal {C}}(\{x\}, \mathcal {E})$ restricts to an equivalence from the full subcategory ![]() ${\text {Fun}}_{/\mathcal {C}}^{F{\text {-cart}}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$.
${\text {Fun}}_{/\mathcal {C}}^{F{\text {-cart}}}(\mathcal {C}_{/x}^{F}, \mathcal {E})$.
Construction 2.3.12 Since ![]() $\mathcal {Y}_{c}$ corresponds to a right
$\mathcal {Y}_{c}$ corresponds to a right ![]() $F$-coadjointable functor, it has cartesian morphisms over
$F$-coadjointable functor, it has cartesian morphisms over ![]() $\mathcal {C}_{F}$. Applying Lemma 2.3.11 to
$\mathcal {C}_{F}$. Applying Lemma 2.3.11 to ![]() $\mathcal {Y}_{c}$ and
$\mathcal {Y}_{c}$ and ![]() $x = c$, we see that there is a unique commutative square
$x = c$, we see that there is a unique commutative square

such that the top horizontal functor preserves cartesian morphisms over ![]() $\mathcal {C}_{F}$ and takes
$\mathcal {C}_{F}$ and takes ![]() ${\text {id}}_{c}$ in
${\text {id}}_{c}$ in ![]() $\mathcal {C}_{/c}^{F}$ to the identity morphism
$\mathcal {C}_{/c}^{F}$ to the identity morphism ![]() ${\text {id}}_{i(c)}$ in
${\text {id}}_{i(c)}$ in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})(i(c),i(c)) \simeq \mathcal {Y}_{c,c}$.
$\operatorname {SPAN}_{F}(\mathcal {C})(i(c),i(c)) \simeq \mathcal {Y}_{c,c}$.
Now since ![]() $\mathcal {Y}_{c} \to \mathcal {C}$ is also a cocartesian fibration, we can extend this to a unique functor from the free cocartesian fibration [Reference Gepner, Haugseng and NikolausGHN17, Theorem 4.5]
$\mathcal {Y}_{c} \to \mathcal {C}$ is also a cocartesian fibration, we can extend this to a unique functor from the free cocartesian fibration [Reference Gepner, Haugseng and NikolausGHN17, Theorem 4.5]
giving a unique commutative triangle

where the horizontal functor preserves cocartesian morphisms and restricts to ![]() $\alpha _{c}^{-}$ on
$\alpha _{c}^{-}$ on ![]() $\mathcal {C}_{/c}^{F}$.
$\mathcal {C}_{/c}^{F}$.
Remark 2.3.13 To understand the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$, we are going to show that the functor
$\operatorname {SPAN}_{F}(\mathcal {C})$, we are going to show that the functor ![]() $\alpha _{c}$ is an equivalence. The explicit construction of the
$\alpha _{c}$ is an equivalence. The explicit construction of the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {B}_{c}$ in (14) allows us to unpack it easily, revealing the expected definition of spans. We carry this out as follows.
$\mathcal {B}_{c}$ in (14) allows us to unpack it easily, revealing the expected definition of spans. We carry this out as follows.
• An object of
 $\mathcal {B}_{c}$ consists of an object
$\mathcal {B}_{c}$ consists of an object  $x \xrightarrow {f} c$ in
$x \xrightarrow {f} c$ in  $\mathcal {C}^{F}_{/c}$, i.e. a morphism
$\mathcal {C}^{F}_{/c}$, i.e. a morphism  $f$ to
$f$ to  $c$ in
$c$ in  $\mathcal {C}_{F}$, together with a morphism from
$\mathcal {C}_{F}$, together with a morphism from  $x$ in
$x$ in  $\mathcal {C}$; in other words, it is precisely a span
with
$\mathcal {C}$; in other words, it is precisely a span
with \[ y \xleftarrow{g} x \xrightarrow{f} c \]
\[ y \xleftarrow{g} x \xrightarrow{f} c \]
 $f$ in
$f$ in  $\mathcal {C}_{F}$. The functor (14) to
$\mathcal {C}_{F}$. The functor (14) to  $\mathcal {C}$ takes this to the object
$\mathcal {C}$ takes this to the object  $y$.
$y$.• A morphism from this object to another object
in the fibre \[ y \xleftarrow{g'} x' \xrightarrow{f'} c \]
\[ y \xleftarrow{g'} x' \xrightarrow{f'} c \]
 $\mathcal {B}_{y,c}$ consists of a morphism
in
$\mathcal {B}_{y,c}$ consists of a morphism
in
 $\mathcal {C}_{/c}$ and a commutative triangle
in
$\mathcal {C}_{/c}$ and a commutative triangle
in
 $\mathcal {C}$, i.e. precisely a morphism of spans
$\mathcal {C}$, i.e. precisely a morphism of spans

• Moreover, the cocartesian morphism over
 $y \xrightarrow {\eta } y'$ in
$y \xrightarrow {\eta } y'$ in  $\mathcal {C}$ is given by composition in
$\mathcal {C}$ is given by composition in  $\mathcal {C}^{[1]}$ and so takes the span
to
$\mathcal {C}^{[1]}$ and so takes the span
to \[ y \xleftarrow{g} x \xrightarrow{f} c \]
\[ y \xleftarrow{g} x \xrightarrow{f} c \]
 \[ y' \xleftarrow{\eta g} x \xrightarrow{f} c. \]
\[ y' \xleftarrow{\eta g} x \xrightarrow{f} c. \]
To prove that ![]() $\alpha _{c}$ is an equivalence we want to use the universal property of
$\alpha _{c}$ is an equivalence we want to use the universal property of ![]() $\mathcal {Y}_{c}$ (i.e. the Yoneda lemma) to produce a functor
$\mathcal {Y}_{c}$ (i.e. the Yoneda lemma) to produce a functor ![]() $\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$, which will be the inverse of
$\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$, which will be the inverse of ![]() $\alpha _{c}$. This requires knowing the following.
$\alpha _{c}$. This requires knowing the following.
Proposition 2.3.14 The functor ![]() $B_{c} \colon \mathcal {C} \to {\text {Cat}}_\infty$ classifying the cocartesian fibration
$B_{c} \colon \mathcal {C} \to {\text {Cat}}_\infty$ classifying the cocartesian fibration ![]() $\mathcal {B}_{c} \to \mathcal {C}$ is right
$\mathcal {B}_{c} \to \mathcal {C}$ is right ![]() $F$-coadjointable.
$F$-coadjointable.
Proof. For ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}$, let us denote the value of
$\mathcal {C}$, let us denote the value of ![]() $B_{c}$ at
$B_{c}$ at ![]() $f$ by
$f$ by
here ![]() $\mathcal {B}_{x,c}$ can be identified with the fibre product
$\mathcal {B}_{x,c}$ can be identified with the fibre product ![]() $\mathcal {C}_{/x} \times _{\mathcal {C}} \mathcal {C}^{F}_{/c}$, and the functor
$\mathcal {C}_{/x} \times _{\mathcal {C}} \mathcal {C}^{F}_{/c}$, and the functor ![]() $f_{\circledast }$ is given by composing with
$f_{\circledast }$ is given by composing with ![]() $f$ in the first factor, i.e.
$f$ in the first factor, i.e.
We first prove that the functor ![]() $\mathcal {B}_{c} \to \mathcal {C}$ is cartesian over
$\mathcal {B}_{c} \to \mathcal {C}$ is cartesian over ![]() $\mathcal {C}_{F}$. In other words, we must show that for every morphism
$\mathcal {C}_{F}$. In other words, we must show that for every morphism ![]() $\phi \colon y' \to y$ in
$\phi \colon y' \to y$ in ![]() $\mathcal {C}_{F}$, the functor
$\mathcal {C}_{F}$, the functor
has a right adjoint, which we will denote by ![]() $\phi ^{\oplus }$. To see that
$\phi ^{\oplus }$. To see that ![]() $\phi _{\circledast }$ has a right adjoint it suffices (by a reformulation of [Reference LurieLur09, Lemma 5.2.4.1]) to show that for any span
$\phi _{\circledast }$ has a right adjoint it suffices (by a reformulation of [Reference LurieLur09, Lemma 5.2.4.1]) to show that for any span ![]() $\sigma = (y \xleftarrow {g} x \xrightarrow {f} c)$ (
$\sigma = (y \xleftarrow {g} x \xrightarrow {f} c)$ (![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$), the
$\mathcal {C}_{F}$), the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {B}_{y',c/\sigma } := \mathcal {B}_{y',c} \times _{\mathcal {B}_{y,c}} \mathcal {B}_{y,c/\sigma }$ has a terminal object.
$\mathcal {B}_{y',c/\sigma } := \mathcal {B}_{y',c} \times _{\mathcal {B}_{y,c}} \mathcal {B}_{y,c/\sigma }$ has a terminal object.
An object of ![]() $\mathcal {B}_{y',c/\sigma }$ is a commutative diagram of the form
$\mathcal {B}_{y',c/\sigma }$ is a commutative diagram of the form

More formally, we can identify ![]() $\mathcal {B}_{y,c/\sigma }$ with the full subcategory
$\mathcal {B}_{y,c/\sigma }$ with the full subcategory ![]() $\mathcal {C}_{/x} \times _{\mathcal {C}_{/c}} \mathcal {C}^{F}_{/c}$ of
$\mathcal {C}_{/x} \times _{\mathcal {C}_{/c}} \mathcal {C}^{F}_{/c}$ of ![]() $\mathcal {C}_{/x}$ spanned by morphisms
$\mathcal {C}_{/x}$ spanned by morphisms ![]() $x' \to x$ such that
$x' \to x$ such that ![]() $x' \to x \to c$ is in
$x' \to x \to c$ is in ![]() $\mathcal {C}_{F}$. The fibre product
$\mathcal {C}_{F}$. The fibre product ![]() $\mathcal {B}_{y',c/\sigma }$ we can then identify with the full subcategory of
$\mathcal {B}_{y',c/\sigma }$ we can then identify with the full subcategory of ![]() $\mathcal {C}_{/p}$, where
$\mathcal {C}_{/p}$, where ![]() $p$ is the diagram
$p$ is the diagram ![]() $y' \to y \leftarrow x$, spanned by commutative squares
$y' \to y \leftarrow x$, spanned by commutative squares

such that the composite ![]() $x' \to x \to c$ lies in
$x' \to x \to c$ lies in ![]() $\mathcal {C}_{F}$. A terminal object in
$\mathcal {C}_{F}$. A terminal object in ![]() $\mathcal {C}_{/p}$ is precisely a fibre product
$\mathcal {C}_{/p}$ is precisely a fibre product ![]() $x \times _{y} y'$, which exists since by assumption
$x \times _{y} y'$, which exists since by assumption ![]() $\mathcal {C}$ admits all pullback along
$\mathcal {C}$ admits all pullback along ![]() $\phi$. Moreover, this terminal object lies in the full subcategory
$\phi$. Moreover, this terminal object lies in the full subcategory ![]() $\mathcal {B}_{y',c/\sigma }$ since the projection
$\mathcal {B}_{y',c/\sigma }$ since the projection ![]() $x \times _{y} y' \to x$ is a base change of
$x \times _{y} y' \to x$ is a base change of ![]() $\phi$ and so lies in
$\phi$ and so lies in ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
To complete the proof we must show that given a pullback square

in ![]() $\mathcal {C}$ with
$\mathcal {C}$ with ![]() $\phi$ in
$\phi$ in ![]() $\mathcal {C}_{F}$, the Beck–Chevalley transformation
$\mathcal {C}_{F}$, the Beck–Chevalley transformation
is an equivalence. Evaluating at a span ![]() $\tilde {y} \leftarrow x \to c$ this transformation is given by the canonical dashed map in the diagram
$\tilde {y} \leftarrow x \to c$ this transformation is given by the canonical dashed map in the diagram

where the two squares containing squiggly arrows are cartesian. Since the square (
16) is by assumption cartesian, it follows from the pasting lemma for pullback squares that this is indeed an equivalence.
Translating Proposition 2.3.8 through the equivalence of Lemma 2.3.9, we see that Proposition 2.3.14 implies that any object ![]() $X \in \mathcal {B}_{c}$ over
$X \in \mathcal {B}_{c}$ over ![]() $c' \in \mathcal {C}$ corresponds to a morphism
$c' \in \mathcal {C}$ corresponds to a morphism ![]() $\mathcal {Y}_{c'} \to \mathcal {B}_{c}$. In particular, we have the following result.
$\mathcal {Y}_{c'} \to \mathcal {B}_{c}$. In particular, we have the following result.
Corollary 2.3.15 There is a canonical functor ![]() $\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$ over
$\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$ over ![]() $\mathcal {C}$ corresponding to the identity span of
$\mathcal {C}$ corresponding to the identity span of ![]() $c$; this preserves cocartesian morphisms and cartesian morphisms over
$c$; this preserves cocartesian morphisms and cartesian morphisms over ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
We now need to prove that the functor ![]() $\alpha _{c}$ has the same property.
$\alpha _{c}$ has the same property.
Proposition 2.3.16 The functor ![]() $\alpha _c \colon \mathcal {B}_{c} \rightarrow \mathcal {Y}_{c}$ over
$\alpha _c \colon \mathcal {B}_{c} \rightarrow \mathcal {Y}_{c}$ over ![]() $\mathcal {C}$ preserves cocartesian morphisms and cartesian morphisms over
$\mathcal {C}$ preserves cocartesian morphisms and cartesian morphisms over ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
Remark 2.3.17 For the proof we first need to discuss the naturality of Beck–Chevalley transformations in the following situation: suppose we have a commutative triangle of ![]() $\infty$-categories
$\infty$-categories

where ![]() $p$ and
$p$ and ![]() $q$ have both cartesian and cocartesian morphisms over
$q$ have both cartesian and cocartesian morphisms over ![]() $f \colon a \to b$ in
$f \colon a \to b$ in ![]() $\mathcal {B}$, but
$\mathcal {B}$, but ![]() $F$ does not necessarily preserve these. We write
$F$ does not necessarily preserve these. We write ![]() $f_{!}$ for the cocartesian pushforward and
$f_{!}$ for the cocartesian pushforward and ![]() $f^{*}$ for the cartesian pullback along
$f^{*}$ for the cartesian pullback along ![]() $f$ for both
$f$ for both ![]() $p$ and
$p$ and ![]() $q$ (so the functor
$q$ (so the functor ![]() $f_{!}$ is left adjoint to
$f_{!}$ is left adjoint to ![]() $f^{*}$). Then we can make the following commutative diagrams for
$f^{*}$). Then we can make the following commutative diagrams for ![]() $x \in \mathcal {E}_{a}$,
$x \in \mathcal {E}_{a}$, ![]() $y \in \mathcal {E}_{b}$.
$y \in \mathcal {E}_{b}$.

In particular, the top left and bottom right squares here encode the compatibility of ![]() $F$ with the units and counits of the two adjunctions
$F$ with the units and counits of the two adjunctions ![]() $f_{!} \dashv f^{*}$. Now suppose we have a commutative square
$f_{!} \dashv f^{*}$. Now suppose we have a commutative square

where ![]() $p$ and
$p$ and ![]() $q$ have cocartesian morphisms over
$q$ have cocartesian morphisms over ![]() $f,f'$ and both cartesian and cocartesian morphisms over
$f,f'$ and both cartesian and cocartesian morphisms over ![]() $g,g'$. Then we claim that the two Beck–Chevalley transformations
$g,g'$. Then we claim that the two Beck–Chevalley transformations ![]() $f'_{!}g'^{*} \to g^{*}f_{!}$, intertwined by
$f'_{!}g'^{*} \to g^{*}f_{!}$, intertwined by ![]() $F$, are related by a commutative diagram
$F$, are related by a commutative diagram

This can be extracted from the following diagram, where we have used (
17) together with naturality:

Proof of Proposition 2.3.16 The universal property we used to define ![]() $\alpha _{c}$ implies that it preserves cocartesian morphisms. Moreover, since
$\alpha _{c}$ implies that it preserves cocartesian morphisms. Moreover, since ![]() $\alpha _{c}$ was extended from a functor
$\alpha _{c}$ was extended from a functor ![]() $\mathcal {C}^{F}_{/c} \to \mathcal {Y}_{c}$ that preserved cartesian morphisms over
$\mathcal {C}^{F}_{/c} \to \mathcal {Y}_{c}$ that preserved cartesian morphisms over ![]() $\mathcal {C}_{F}$, we know
$\mathcal {C}_{F}$, we know ![]() $\alpha _{c}$ preserves cartesian morphisms in the image of
$\alpha _{c}$ preserves cartesian morphisms in the image of ![]() $\mathcal {C}_{/c}^{F}$. In other words, for
$\mathcal {C}_{/c}^{F}$. In other words, for ![]() $f \colon x \to c$ in
$f \colon x \to c$ in ![]() $\mathcal {C}_{F}$, the map
$\mathcal {C}_{F}$, the map ![]() $\alpha _{c}(\phi ^{\oplus }[h]_{F}) \to \phi ^{\oplus }\alpha _{c}([h]_{F})$ is an equivalence for all
$\alpha _{c}(\phi ^{\oplus }[h]_{F}) \to \phi ^{\oplus }\alpha _{c}([h]_{F})$ is an equivalence for all ![]() $\phi \colon x' \to x$ in
$\phi \colon x' \to x$ in ![]() $\mathcal {C}_{F}$.
$\mathcal {C}_{F}$.
More generally, for a span ![]() $\sigma = (y \xleftarrow {g} x \xrightarrow {f} c)$, we need to show that
$\sigma = (y \xleftarrow {g} x \xrightarrow {f} c)$, we need to show that ![]() $\alpha _c(\phi ^{\oplus }\sigma ) \simeq \phi ^{\oplus }\alpha _c(\sigma )$ for any morphism
$\alpha _c(\phi ^{\oplus }\sigma ) \simeq \phi ^{\oplus }\alpha _c(\sigma )$ for any morphism ![]() $\phi \colon y' \to y$ in
$\phi \colon y' \to y$ in ![]() $\mathcal {C}_{F}$. To proceed, let us view
$\mathcal {C}_{F}$. To proceed, let us view ![]() $\sigma$ as
$\sigma$ as ![]() $g_{\circledast }[f]_{F}$.
$g_{\circledast }[f]_{F}$.
Forming the pullback square

the Beck–Chevalley transformation yields an equivalence:
Moreover, from (18) we get a natural commutative diagram

where the map labelled (1) is an equivalence since ![]() $\alpha _{c}$ preserves cartesian morphisms from
$\alpha _{c}$ preserves cartesian morphisms from ![]() $\mathcal {C}^{F}_{/c}$, those labelled (2) are equivalences since
$\mathcal {C}^{F}_{/c}$, those labelled (2) are equivalences since ![]() $\alpha _{c}$ preserves cocartesian morphisms, and those labelled (3) are equivalences because the Beck–Chevalley transformations are invertible. Hence, the last morphism in the diagram is also an equivalence, which shows that
$\alpha _{c}$ preserves cocartesian morphisms, and those labelled (3) are equivalences because the Beck–Chevalley transformations are invertible. Hence, the last morphism in the diagram is also an equivalence, which shows that ![]() $\alpha _{c}$ preserves the cartesian morphism
$\alpha _{c}$ preserves the cartesian morphism ![]() $\phi ^{\oplus }g_{\circledast }[f]_{F} \to g_{\circledast }[f]_{F}$.
$\phi ^{\oplus }g_{\circledast }[f]_{F} \to g_{\circledast }[f]_{F}$.
Corollary 2.3.18 The functors ![]() $\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$ and
$\beta _{c} \colon \mathcal {Y}_{c} \to \mathcal {B}_{c}$ and ![]() $\alpha _{c} \colon \mathcal {B}_{c} \to \mathcal {Y}_{c}$ satisfy
$\alpha _{c} \colon \mathcal {B}_{c} \to \mathcal {Y}_{c}$ satisfy
Thus, ![]() $\alpha _{c}$ is an equivalence with inverse
$\alpha _{c}$ is an equivalence with inverse ![]() $\beta _{c}$.
$\beta _{c}$.
Proof. By construction ![]() $\alpha _{c}$ takes the identity span of
$\alpha _{c}$ takes the identity span of ![]() $c$ to
$c$ to
The composite ![]() $\beta _{c}\alpha _{c}$ is a functor
$\beta _{c}\alpha _{c}$ is a functor ![]() $\mathcal {B}_{c} \to \mathcal {B}_{c}$ that preserves cocartesian morphisms, hence it is determined by its restriction to
$\mathcal {B}_{c} \to \mathcal {B}_{c}$ that preserves cocartesian morphisms, hence it is determined by its restriction to ![]() $\mathcal {C}^{F}_{/c} \to \mathcal {B}_{c}$. This restriction preserves cartesian morphisms over
$\mathcal {C}^{F}_{/c} \to \mathcal {B}_{c}$. This restriction preserves cartesian morphisms over ![]() $\mathcal {C}_{F}$ and so by Lemma 2.3.11 it is determined by its value at
$\mathcal {C}_{F}$ and so by Lemma 2.3.11 it is determined by its value at ![]() ${\text {id}}_{c}$, which is the identity span in
${\text {id}}_{c}$, which is the identity span in ![]() $\mathcal {B}_{c}$. The same holds for the identity of
$\mathcal {B}_{c}$. The same holds for the identity of ![]() $\mathcal {B}_{c}$ and so
$\mathcal {B}_{c}$ and so ![]() ${\text {id}}_{\mathcal {B}_{c}} \simeq \beta _{c}\alpha _{c}$. Conversely,
${\text {id}}_{\mathcal {B}_{c}} \simeq \beta _{c}\alpha _{c}$. Conversely, ![]() $\alpha _{c}\beta _{c}$ is a functor
$\alpha _{c}\beta _{c}$ is a functor ![]() $\mathcal {Y}_{c} \to \mathcal {Y}_{c}$ that preserves cocartesian morphisms and cartesian morphisms over
$\mathcal {Y}_{c} \to \mathcal {Y}_{c}$ that preserves cocartesian morphisms and cartesian morphisms over ![]() $\mathcal {C}_{F}$ by Proposition 2.3.16. By Proposition 2.3.8, interpreted in terms of fibrations, this functor is determined by where it sends the identity of
$\mathcal {C}_{F}$ by Proposition 2.3.16. By Proposition 2.3.8, interpreted in terms of fibrations, this functor is determined by where it sends the identity of ![]() $c$; since we know this is taken to itself, this functor must be the identity
$c$; since we know this is taken to itself, this functor must be the identity ![]() ${\text {id}}_{\mathcal {Y}_{c}}$.
${\text {id}}_{\mathcal {Y}_{c}}$.
The equivalence ![]() $\mathcal {Y}_{c}\simeq \mathcal {B}_{c}$ allows us to identify morphisms in
$\mathcal {Y}_{c}\simeq \mathcal {B}_{c}$ allows us to identify morphisms in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ with spans, and 2-morphisms with morphisms of spans. We now check that composition of spans works as expected.
$\operatorname {SPAN}_{F}(\mathcal {C})$ with spans, and 2-morphisms with morphisms of spans. We now check that composition of spans works as expected.
Proposition 2.3.19 Composition of spans in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ is given by taking pullbacks.
$\operatorname {SPAN}_{F}(\mathcal {C})$ is given by taking pullbacks.
Proof. By construction, the cocartesian morphisms in ![]() $\mathcal {Y}_{c}$ encode precomposition with the images of morphisms in
$\mathcal {Y}_{c}$ encode precomposition with the images of morphisms in ![]() $\mathcal {C}^{{\text {op}}}$ under the functor
$\mathcal {C}^{{\text {op}}}$ under the functor ![]() $i$: given a morphism
$i$: given a morphism ![]() $g \colon x \to y$ in
$g \colon x \to y$ in ![]() $\mathcal {C}$ we have
$\mathcal {C}$ we have
for any span ![]() $\sigma$. In particular, from our description of the right-hand side we have
$\sigma$. In particular, from our description of the right-hand side we have
and, more generally,
This means that to describe an arbitrary composition in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ it suffices (by associativity of composition) to understand compositions of the form
$\operatorname {SPAN}_{F}(\mathcal {C})$ it suffices (by associativity of composition) to understand compositions of the form ![]() $[g]_{B} \circ [f]_{F}$. Note that
$[g]_{B} \circ [f]_{F}$. Note that ![]() $[f]_{B}$ is in the image of
$[f]_{B}$ is in the image of ![]() $\mathcal {C}_{F}^{{\text {op}}}$ under
$\mathcal {C}_{F}^{{\text {op}}}$ under ![]() $i$, and therefore admits a left adjoint in
$i$, and therefore admits a left adjoint in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ since
$\operatorname {SPAN}_{F}(\mathcal {C})$ since ![]() $i$ is left
$i$ is left ![]() $F$-adjointable; let us denote this by
$F$-adjointable; let us denote this by ![]() $[f]_{B}^{\ell }$. We claim that
$[f]_{B}^{\ell }$. We claim that
To see this, we note that precomposition with ![]() $[f]_{B}$ is the functor
$[f]_{B}$ is the functor ![]() $f_{\circledast }$, which admits a right adjoint
$f_{\circledast }$, which admits a right adjoint ![]() $f^{\oplus }$. Therefore, by uniqueness of adjoints we conclude that precomposition with
$f^{\oplus }$. Therefore, by uniqueness of adjoints we conclude that precomposition with ![]() $[f]^{\ell }_{B}$ must coincide with
$[f]^{\ell }_{B}$ must coincide with ![]() $f^{\oplus }$. Therefore, the span
$f^{\oplus }$. Therefore, the span ![]() $[f]^{\ell }_{B}$ is computed as
$[f]^{\ell }_{B}$ is computed as
Furthermore,
which we saw above is computed by taking the pullback of ![]() $g$ along
$g$ along ![]() $f$, as required.
$f$, as required.
Proposition 2.3.20 A span ![]() $\sigma = (y \xleftarrow {g} x \xrightarrow {f} z)$ is invertible as a morphism in
$\sigma = (y \xleftarrow {g} x \xrightarrow {f} z)$ is invertible as a morphism in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ if and only if the components
$\operatorname {SPAN}_{F}(\mathcal {C})$ if and only if the components ![]() $f$ and
$f$ and ![]() $g$ are both invertible in
$g$ are both invertible in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Since we now know composition is given by taking pullbacks, this follows as in the proof of [Reference HaugsengHau18, Lemma 8.2].
Corollary 2.3.21 The functor ![]() $i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives an equivalence on underlying
$i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ gives an equivalence on underlying ![]() $\infty$-groupoids
$\infty$-groupoids
Proof. We know the functor ![]() $i$ is essentially surjective on objects, so it is enough to show that for any objects
$i$ is essentially surjective on objects, so it is enough to show that for any objects ![]() $x,y$ the map
$x,y$ the map
is an equivalence, where we are taking the components of the mapping spaces that correspond to equivalences. This is immediate from Proposition 2.3.20 and our description of the mapping spaces in ![]() $\operatorname {Span}_{F}(\mathcal {C})$.
$\operatorname {Span}_{F}(\mathcal {C})$.
Combining the results of this section, we have shown the following.
Theorem 2.3.22 Let ![]() $(\mathcal {C}, \mathcal {C}_{F})$ be a span triple. Then left
$(\mathcal {C}, \mathcal {C}_{F})$ be a span triple. Then left ![]() $F$-adjointable functors out of
$F$-adjointable functors out of ![]() $\mathcal {C}^{{\text {op}}}$ are corepresented by an
$\mathcal {C}^{{\text {op}}}$ are corepresented by an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ via a left
$\operatorname {SPAN}_{F}(\mathcal {C})$ via a left ![]() $F$-adjointable functor
$F$-adjointable functor ![]() $i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ with the following properties:
$i \colon \mathcal {C}^{{\text {op}}} \to \operatorname {SPAN}_{F}(\mathcal {C})$ with the following properties:
(i)
 $i$ gives an equivalence
on underlying
$i$ gives an equivalence
on underlying \[ \operatorname{SPAN}_{F}(\mathcal{C})^{\simeq} \simeq \mathcal{C}^{\simeq} \]
\[ \operatorname{SPAN}_{F}(\mathcal{C})^{\simeq} \simeq \mathcal{C}^{\simeq} \]
 $\infty$-groupoids;
$\infty$-groupoids;(ii) morphisms from
 $i(x)$ to
$i(x)$ to  $i(y)$ can be identified with spans
where
$i(y)$ can be identified with spans
where \[ y \xleftarrow{g} x \xrightarrow{f} z \]
\[ y \xleftarrow{g} x \xrightarrow{f} z \]
 $f$ is in
$f$ is in  $\mathcal {C}_{F}$;
$\mathcal {C}_{F}$;(iii) 2-morphisms correspond to morphisms of spans diagrams; and
(iv) composition of morphisms is given by taking pullbacks.
We end this section by deducing a description of the functor of ![]() $(\infty,2)$-categories corresponding to a left
$(\infty,2)$-categories corresponding to a left ![]() $F$-adjointable functor.
$F$-adjointable functor.
Proposition 2.3.23 For a left ![]() $F$-adjointable functor
$F$-adjointable functor ![]() $\phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$, the corresponding functor
$\phi \colon \mathcal {C}^{{\text {op}}} \to \mathcal {X}$, the corresponding functor ![]() $\Phi \colon \operatorname {SPAN}_{F}(\mathcal {C}) \to \mathcal {X}$ can be described as follows.
$\Phi \colon \operatorname {SPAN}_{F}(\mathcal {C}) \to \mathcal {X}$ can be described as follows.
(1) On objects,
 $\Phi (c) \simeq \phi (c)$ for
$\Phi (c) \simeq \phi (c)$ for  $c \in \mathcal {C}$.
$c \in \mathcal {C}$.(2) On morphisms,
 $\Phi$ takes a span
to the composite
$\Phi$ takes a span
to the composite \[ \sigma = (y \xleftarrow{g} x \xrightarrow{f} z) \]
\[ \sigma = (y \xleftarrow{g} x \xrightarrow{f} z) \]
 $f_{\oplus }g^{\circledast } \colon \phi (x) \to \phi (y)$, where
$f_{\oplus }g^{\circledast } \colon \phi (x) \to \phi (y)$, where  $f_{\oplus }$ is the left adjoint to
$f_{\oplus }$ is the left adjoint to  $f^{\circledast } := \phi (f)$.
$f^{\circledast } := \phi (f)$.(3) On 2-morphisms,
 $\Phi$ takes the 2-morphism
$\Phi$ takes the 2-morphism  $\beta \colon \sigma \to \sigma '$ given by the commutative diagram
to the composite
$\beta \colon \sigma \to \sigma '$ given by the commutative diagram
to the composite (19)where the first noninvertible arrow is an adjunction unit and the second noninvertible arrow is a counit.
(19)where the first noninvertible arrow is an adjunction unit and the second noninvertible arrow is a counit. \begin{equation} f_{\oplus}g^{\circledast} \simeq f_{\oplus}h^{\circledast}g'^{\circledast} \to f_{\oplus}h^{\circledast}f'^{\circledast}f'_{\oplus}g'^{\circledast} \simeq f_{\oplus}f^{\circledast}f'_{\oplus}g'^{\circledast} \to f'_{\oplus}g'^{\circledast}, \end{equation}
\begin{equation} f_{\oplus}g^{\circledast} \simeq f_{\oplus}h^{\circledast}g'^{\circledast} \to f_{\oplus}h^{\circledast}f'^{\circledast}f'_{\oplus}g'^{\circledast} \simeq f_{\oplus}f^{\circledast}f'_{\oplus}g'^{\circledast} \to f'_{\oplus}g'^{\circledast}, \end{equation}
Proof. We know that ![]() $\Phi \circ i \simeq \phi$ and that
$\Phi \circ i \simeq \phi$ and that ![]() $i$ is an equivalence on underlying
$i$ is an equivalence on underlying ![]() $\infty$-groupoids by Corollary 2.3.21, which gives part (1). To prove part (2), observe that the bispan
$\infty$-groupoids by Corollary 2.3.21, which gives part (1). To prove part (2), observe that the bispan ![]() $\sigma$ is the composite
$\sigma$ is the composite ![]() $[f]_{F} \circ [g]_{B}$ in
$[f]_{F} \circ [g]_{B}$ in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$. Here
$\operatorname {SPAN}_{F}(\mathcal {C})$. Here ![]() $[g]_{B}$ is
$[g]_{B}$ is ![]() $i(g)$, and so
$i(g)$, and so
Moreover, the span ![]() $[f]_{F}$ is left adjoint to
$[f]_{F}$ is left adjoint to ![]() $[f]_{B}$, hence its image
$[f]_{B}$, hence its image ![]() $\Phi ([f]_{F})$ is the left adjoint
$\Phi ([f]_{F})$ is the left adjoint ![]() $f_{\oplus }$ to
$f_{\oplus }$ to ![]() $f^{\circledast }$. In other words, we have
$f^{\circledast }$. In other words, we have ![]() $\Phi (\sigma ) \simeq \Phi ([f]_{F}) \circ \Phi ([g]_{B}) \simeq f_{\oplus }g^{\circledast }$. To prove part (3), first observe that the 2-morphism
$\Phi (\sigma ) \simeq \Phi ([f]_{F}) \circ \Phi ([g]_{B}) \simeq f_{\oplus }g^{\circledast }$. To prove part (3), first observe that the 2-morphism ![]() $\beta$ is the composite (‘whiskering’) of the morphism
$\beta$ is the composite (‘whiskering’) of the morphism ![]() $[g']_{B}$ with the 2-morphism
$[g']_{B}$ with the 2-morphism ![]() $\lambda$ given by
$\lambda$ given by

and this whiskering corresponds to the first equivalence in (19).
It thus suffices to show that ![]() $\Phi$ takes
$\Phi$ takes ![]() $\lambda$ to the composite
$\lambda$ to the composite
using the unit for ![]() $f'_{\oplus } \dashv f'^{\circledast }$ and the counit for
$f'_{\oplus } \dashv f'^{\circledast }$ and the counit for ![]() $f_{\oplus } \dashv f^{\circledast }$. To show this we will check that the morphism
$f_{\oplus } \dashv f^{\circledast }$. To show this we will check that the morphism ![]() $\lambda$ has the corresponding decomposition in
$\lambda$ has the corresponding decomposition in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$. Indeed, we can decompose
$\operatorname {SPAN}_{F}(\mathcal {C})$. Indeed, we can decompose ![]() $\lambda$ as the composite
$\lambda$ as the composite

where ![]() $\pi,\pi '$ are the projections from
$\pi,\pi '$ are the projections from ![]() $x' \times _{z} x$ to
$x' \times _{z} x$ to ![]() $x$ and
$x$ and ![]() $x'$, respectively, and
$x'$, respectively, and ![]() $\phi$ is the unique morphism such that
$\phi$ is the unique morphism such that ![]() $\pi \phi \simeq {\text {id}}_{x}$,
$\pi \phi \simeq {\text {id}}_{x}$, ![]() $\pi '\phi \simeq h$. Now unpacking the description of units and counits in
$\pi '\phi \simeq h$. Now unpacking the description of units and counits in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ implies that the top morphism in this decomposition is the composite of the unit for
$\operatorname {SPAN}_{F}(\mathcal {C})$ implies that the top morphism in this decomposition is the composite of the unit for ![]() $[f']_{F} \dashv [f']_{B}$ with the morphism
$[f']_{F} \dashv [f']_{B}$ with the morphism ![]() $x' \xleftarrow {h} x \xrightarrow {f} z$ and the bottom is the composite of
$x' \xleftarrow {h} x \xrightarrow {f} z$ and the bottom is the composite of ![]() $[f']_{F}$ with the counit for
$[f']_{F}$ with the counit for ![]() $[f]_{F} \dashv [f]_{B}$.
$[f]_{F} \dashv [f]_{B}$.
2.4 Distributive functors
We now start our discussion of distributivity. In this section we introduce the notion of a distributive functor, which we will prove in the next subsection is corepresented by ![]() $(\infty,2)$-categories of bispans. For the definition we first need to introduce the notion of a distributivity diagram, which dictates how the multiplicative and additive pushforwards for a distributive functor should interact.
$(\infty,2)$-categories of bispans. For the definition we first need to introduce the notion of a distributivity diagram, which dictates how the multiplicative and additive pushforwards for a distributive functor should interact.
Definition 2.4.1 Let ![]() $x \xrightarrow {l} y \xrightarrow {f} z$ be morphisms in an
$x \xrightarrow {l} y \xrightarrow {f} z$ be morphisms in an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$. A distributivity diagram for
$\mathcal {C}$. A distributivity diagram for ![]() $l$ and
$l$ and ![]() $f$ is a commutative diagram
$f$ is a commutative diagram

where the square is cartesian, with the property that for any morphism ![]() $\phi \colon u \to z$, the composite map
$\phi \colon u \to z$, the composite map
is an equivalence. The distributivity diagram for ![]() $l$ and
$l$ and ![]() $f$ is necessarily unique if it exists.
$f$ is necessarily unique if it exists.
Remark 2.4.2 Consider the ![]() $\infty$-category of diagrams of shape (20) (with the square cartesian). If all pullbacks along
$\infty$-category of diagrams of shape (20) (with the square cartesian). If all pullbacks along ![]() $f$ exist in
$f$ exist in ![]() $\mathcal {C}$, then this is equivalently an object of the fibre product of
$\mathcal {C}$, then this is equivalently an object of the fibre product of ![]() $\infty$-categories
$\infty$-categories
with the functors in the pullback being ![]() $f^{*} \colon \mathcal {C}_{/z} \to \mathcal {C}_{/y}$ and
$f^{*} \colon \mathcal {C}_{/z} \to \mathcal {C}_{/y}$ and ![]() $l_{!} \colon \mathcal {C}_{/x} \to \mathcal {C}_{/y}$. The universal property of the distributivity diagram can then be reformulated as that of being a terminal object in this
$l_{!} \colon \mathcal {C}_{/x} \to \mathcal {C}_{/y}$. The universal property of the distributivity diagram can then be reformulated as that of being a terminal object in this ![]() $\infty$-category.
$\infty$-category.
Definition 2.4.3 A bispan triple ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consists of an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consists of an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ together with two subcategories
$\mathcal {C}$ together with two subcategories ![]() $\mathcal {C}_{F}, \mathcal {C}_{L}$ such that the following assumptions hold:
$\mathcal {C}_{F}, \mathcal {C}_{L}$ such that the following assumptions hold:
(a)
 $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair;
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair;(b)
 $(\mathcal {C}, \mathcal {C}_{L})$ is a span pair;
$(\mathcal {C}, \mathcal {C}_{L})$ is a span pair;(c) for
 $l \colon x \to y$ in
$l \colon x \to y$ in  $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and  $f \colon y \to z$ in
$f \colon y \to z$ in  $\mathcal {C}_{F}$ there exists a distributivity diagram (20) where
$\mathcal {C}_{F}$ there exists a distributivity diagram (20) where  $g$ is in
$g$ is in  $\mathcal {C}_{L}$ (and, hence,
$\mathcal {C}_{L}$ (and, hence,  $\tilde {f}$ is in
$\tilde {f}$ is in  $\mathcal {C}_{F}$ by assumption (a) and
$\mathcal {C}_{F}$ by assumption (a) and  $\tilde {g}$ is in
$\tilde {g}$ is in  $\mathcal {C}_{L}$ by assumption (b)).
$\mathcal {C}_{L}$ by assumption (b)).
Notation 2.4.4 For ![]() $x \in \mathcal {C}$ we write
$x \in \mathcal {C}$ we write ![]() $\mathcal {C}_{/x}^{L}$ for the full subcategory of
$\mathcal {C}_{/x}^{L}$ for the full subcategory of ![]() $\mathcal {C}_{/x}$ spanned by morphisms
$\mathcal {C}_{/x}$ spanned by morphisms ![]() $y \to x$ in
$y \to x$ in ![]() $\mathcal {C}_{L}$.
$\mathcal {C}_{L}$.
Remark 2.4.5 For a fixed ![]() $f\colon y \to z$ in
$f\colon y \to z$ in ![]() $\mathcal {C}_{F}$, if the distributivity diagram (20) exists for all
$\mathcal {C}_{F}$, if the distributivity diagram (20) exists for all ![]() $l$ in
$l$ in ![]() $\mathcal {C}_{L}$, then the functor
$\mathcal {C}_{L}$, then the functor ![]() $f^{*} \colon \mathcal {C}^{L}_{/z} \to \mathcal {C}^{L}_{/y}$ given by pullback along
$f^{*} \colon \mathcal {C}^{L}_{/z} \to \mathcal {C}^{L}_{/y}$ given by pullback along ![]() $f$ has a right adjoint
$f$ has a right adjoint ![]() $f_{*}$. Indeed, from (21) we see that we have
$f_{*}$. Indeed, from (21) we see that we have
which determines the rest of the diagram. Note, however, that if the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}_{L}$ is not all of
$\mathcal {C}_{L}$ is not all of ![]() $\mathcal {C}$ then the property of (21) is slightly stronger than the existence of the right adjoint: for this to exist it suffices to consider maps from
$\mathcal {C}$ then the property of (21) is slightly stronger than the existence of the right adjoint: for this to exist it suffices to consider maps from ![]() $\phi$ in
$\phi$ in ![]() $\mathcal {C}^{L}_{/z}$, while (21) asks for an equivalence on maps from any
$\mathcal {C}^{L}_{/z}$, while (21) asks for an equivalence on maps from any ![]() $\phi$ in
$\phi$ in ![]() $\mathcal {C}_{/z}$. We can characterize the additional assumption on these right adjoints needed to have a bispan triple in terms of a base change property.
$\mathcal {C}_{/z}$. We can characterize the additional assumption on these right adjoints needed to have a bispan triple in terms of a base change property.
Lemma 2.4.6 Suppose we have a triple ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consisting of an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ consisting of an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ together with two subcategories
$\mathcal {C}$ together with two subcategories ![]() $\mathcal {C}_{F}, \mathcal {C}_{L}$ such that:
$\mathcal {C}_{F}, \mathcal {C}_{L}$ such that:
(a)
 $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair;
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair;(b)
 $(\mathcal {C}, \mathcal {C}_{L})$ is a span pair;
$(\mathcal {C}, \mathcal {C}_{L})$ is a span pair;(c) for any
 $f \colon x \to y$ in
$f \colon x \to y$ in  $\mathcal {C}_{F}$ the functor
$\mathcal {C}_{F}$ the functor  $f^{*} \colon \mathcal {C}^{L}_{/y} \to \mathcal {C}^{L}_{/x}$ given by pullback along
$f^{*} \colon \mathcal {C}^{L}_{/y} \to \mathcal {C}^{L}_{/x}$ given by pullback along  $f$ has a right adjoint
$f$ has a right adjoint  $f_{*}$.
$f_{*}$.
Then ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple if and only if for every cartesian square
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple if and only if for every cartesian square

with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$ the commutative square
$\mathcal {C}_{F}$ the commutative square

is right adjointable, i.e. the mate transformation
is invertible.
Proof. First suppose we have a bispan triple. Then for ![]() $l \in \mathcal {C}^{L}_{/x}$ and
$l \in \mathcal {C}^{L}_{/x}$ and ![]() $l' \in \mathcal {C}^{L}_{/y'}$ we have natural equivalences
$l' \in \mathcal {C}^{L}_{/y'}$ we have natural equivalences
 \begin{align*} {\text {Map}}_{/y'}(l', f'_{*}\xi^{*}l) & \simeq {\text {Map}}_{/x'}(f'^{*}l', \xi^{*}l) \simeq {\text {Map}}_{/x}(\xi_{!}f'^{*}l', l) \\ & \simeq {\text {Map}}_{/x}(f^{*}\eta_{!}l', l) \simeq {\text {Map}}_{/y}(\eta_{!}l', f_{*}l) \\ & \simeq {\text {Map}}_{/y}(l', \eta^{*}f_{*}l), \end{align*}
\begin{align*} {\text {Map}}_{/y'}(l', f'_{*}\xi^{*}l) & \simeq {\text {Map}}_{/x'}(f'^{*}l', \xi^{*}l) \simeq {\text {Map}}_{/x}(\xi_{!}f'^{*}l', l) \\ & \simeq {\text {Map}}_{/x}(f^{*}\eta_{!}l', l) \simeq {\text {Map}}_{/y}(\eta_{!}l', f_{*}l) \\ & \simeq {\text {Map}}_{/y}(l', \eta^{*}f_{*}l), \end{align*}
using the functors ![]() $\eta _{!}$ and
$\eta _{!}$ and ![]() $\xi _{!}$ given by composition with
$\xi _{!}$ given by composition with ![]() $\eta$ and
$\eta$ and ![]() $\xi$, respectively, which act as left adjoints to
$\xi$, respectively, which act as left adjoints to ![]() $\eta ^{*}$ and
$\eta ^{*}$ and ![]() $\xi ^{*}$ when pullbacks along
$\xi ^{*}$ when pullbacks along ![]() $\eta$ and
$\eta$ and ![]() $\xi$ exist, and the full strength of condition (21) for distributivity diagrams, which implies that we have the second-to-last equivalence even though
$\xi$ exist, and the full strength of condition (21) for distributivity diagrams, which implies that we have the second-to-last equivalence even though ![]() $\eta _{!}l'$ is not necessarily in
$\eta _{!}l'$ is not necessarily in ![]() $\mathcal {C}_{L}$.
$\mathcal {C}_{L}$.
Now suppose our triple satisfies the assumption on Beck–Chevalley transformations. To check that it is a bispan triple we must show that for ![]() $l \colon c \to x$ in
$l \colon c \to x$ in ![]() $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$ the pushforward
$\mathcal {C}_{F}$ the pushforward ![]() $f_{*}l$ has the universal property (21), i.e. that for every morphism
$f_{*}l$ has the universal property (21), i.e. that for every morphism ![]() $\eta \colon y' \to y$ we have a natural equivalence
$\eta \colon y' \to y$ we have a natural equivalence
Denoting the pullback square containing ![]() $\eta$ and
$\eta$ and ![]() $f$ as above, we have
$f$ as above, we have
 \begin{align*} {\text {Map}}_{/y}(\eta, f_{*}l) & \simeq {\text {Map}}_{/y}(\eta_{!}{\text {id}}_{y'}, f_{*}l) \simeq {\text {Map}}_{/y'}({\text {id}}_{y'}, \eta^{*}f_{*}l) \\ & \simeq {\text {Map}}_{/y'}({\text {id}}_{y'}, f'_{*}\xi^{*}l) \simeq {\text {Map}}_{/x'}(f'^{*}{\text {id}}_{y'}, \xi^{*}l) \\ & \simeq {\text {Map}}_{/x'}({\text {id}}_{x'}, \xi^{*}l) \simeq {\text {Map}}_{/x}(\xi_{!}{\text {id}}_{x'}, l) \\ & \simeq {\text {Map}}_{/x}(f^{*}\eta, l), \end{align*}
\begin{align*} {\text {Map}}_{/y}(\eta, f_{*}l) & \simeq {\text {Map}}_{/y}(\eta_{!}{\text {id}}_{y'}, f_{*}l) \simeq {\text {Map}}_{/y'}({\text {id}}_{y'}, \eta^{*}f_{*}l) \\ & \simeq {\text {Map}}_{/y'}({\text {id}}_{y'}, f'_{*}\xi^{*}l) \simeq {\text {Map}}_{/x'}(f'^{*}{\text {id}}_{y'}, \xi^{*}l) \\ & \simeq {\text {Map}}_{/x'}({\text {id}}_{x'}, \xi^{*}l) \simeq {\text {Map}}_{/x}(\xi_{!}{\text {id}}_{x'}, l) \\ & \simeq {\text {Map}}_{/x}(f^{*}\eta, l), \end{align*}
where the fourth equivalence holds because ![]() ${\text {id}}_{y'}$ is in
${\text {id}}_{y'}$ is in ![]() $\mathcal {C}_{L}$.
$\mathcal {C}_{L}$.
Remark 2.4.7 If ![]() $\mathcal {C}$ is locally cartesian closed, then all distributivity diagrams exist in
$\mathcal {C}$ is locally cartesian closed, then all distributivity diagrams exist in ![]() $\mathcal {C}$ for any choice of
$\mathcal {C}$ for any choice of ![]() $\mathcal {C}_{L}$; this is the case if
$\mathcal {C}_{L}$; this is the case if ![]() $\mathcal {C}$ is an
$\mathcal {C}$ is an ![]() $\infty$-topos, for example.
$\infty$-topos, for example.
Notation 2.4.8 We use the following notation for a functor ![]() $\Phi \colon\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$: for any morphism
$\Phi \colon\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$: for any morphism ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}$, we write
$\mathcal {C}$, we write
and if ![]() $f$ lies in
$f$ lies in ![]() $\mathcal {C}_{F}$ we also write
$\mathcal {C}_{F}$ we also write
For the next definitions we fix a bispan triple ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$, an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$, an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$, and a functor
$\mathcal {X}$, and a functor
Definition 2.4.9 Given ![]() $l \colon x \to y$ in
$l \colon x \to y$ in ![]() $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and ![]() $f \colon y \to z$ in
$f \colon y \to z$ in ![]() $\mathcal {C}_{F}$, we have by assumption a distributivity diagram as in (20) in
$\mathcal {C}_{F}$, we have by assumption a distributivity diagram as in (20) in ![]() $\mathcal {C}$. If
$\mathcal {C}$. If ![]() $\Phi |_{\mathcal {C}^{{\text {op}}}}$ is left
$\Phi |_{\mathcal {C}^{{\text {op}}}}$ is left ![]() $L$-adjointable we define the distributivity transformation for
$L$-adjointable we define the distributivity transformation for ![]() $l$ and
$l$ and ![]() $f$ as the composite
$f$ as the composite
where the first map uses the unit for the adjunction ![]() $l_\oplus \dashv l^\circledast$, the second equivalence uses the functoriality of
$l_\oplus \dashv l^\circledast$, the second equivalence uses the functoriality of ![]() $\Phi$ for compositions of spans, and the last map uses the counit of the adjunction
$\Phi$ for compositions of spans, and the last map uses the counit of the adjunction ![]() $g_\oplus \dashv g^\circledast$.
$g_\oplus \dashv g^\circledast$.
Definition 2.4.10 We say the functor ![]() $\Phi$ is
$\Phi$ is ![]() $L$-distributive if
$L$-distributive if ![]() $\Phi |_{\mathcal {C}^{{\text {op}}}}$ is left
$\Phi |_{\mathcal {C}^{{\text {op}}}}$ is left ![]() $L$-adjointable, and the distributivity transformation (22) is an equivalence for all
$L$-adjointable, and the distributivity transformation (22) is an equivalence for all ![]() $l$ in
$l$ in ![]() $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$. If the context is clear, we simply call
$\mathcal {C}_{F}$. If the context is clear, we simply call ![]() $\Phi$ distributive. We write
$\Phi$ distributive. We write
for the subspace spanned by the ![]() $L$-distributive functors.
$L$-distributive functors.
Remark 2.4.11 The distributivity transformation (22) is precisely the mate transformation for the following commutative square:

We can therefore reformulate the condition for the functor ![]() $\Phi$ to be
$\Phi$ to be ![]() $L$-distributive as: for every distributivity diagram (20), the square (
$L$-distributive as: for every distributivity diagram (20), the square (
) is left adjointable.
Variant 2.4.12 Let ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ be a bispan triple and
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ be a bispan triple and ![]() $\mathcal {X}$ an
$\mathcal {X}$ an ![]() $(\infty,2)$-category. We say that a functor
$(\infty,2)$-category. We say that a functor ![]() $\Phi \colon \operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}} \to \mathcal {X}$ is
$\Phi \colon \operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}} \to \mathcal {X}$ is ![]() $L$-codistributive if the opposite functor
$L$-codistributive if the opposite functor
is ![]() $L$-distributive. Similarly, we say that a functor
$L$-distributive. Similarly, we say that a functor ![]() $\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$ is right
$\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$ is right ![]() $L$-distributive if the functor
$L$-distributive if the functor
is ![]() $L$-distributive. Since left adjoints in
$L$-distributive. Since left adjoints in ![]() $\mathcal {X}^{2{\text {-op}}}$ correspond to right adjoints in
$\mathcal {X}^{2{\text {-op}}}$ correspond to right adjoints in ![]() $\mathcal {X}$, this amounts to: for every morphism
$\mathcal {X}$, this amounts to: for every morphism ![]() $l \in \mathcal {C}_{L}$ the morphism
$l \in \mathcal {C}_{L}$ the morphism ![]() $l^{\circledast }$ has a right adjoint
$l^{\circledast }$ has a right adjoint ![]() $l_{\circledast }$, and the restriction of
$l_{\circledast }$, and the restriction of ![]() $\Phi$ to
$\Phi$ to ![]() $\mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is right
$\mathcal {C}^{{\text {op}}} \to \mathcal {X}$ is right ![]() $L$-adjointable. Moreover, given a distributivity diagram as in (20) with
$L$-adjointable. Moreover, given a distributivity diagram as in (20) with ![]() $l$ in
$l$ in ![]() $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$, we have a right distributivity transformation
$\mathcal {C}_{F}$, we have a right distributivity transformation
which is required to be an equivalence.
Just as for adjointability, there is a natural notion of an ![]() $L$-distributive transformation.
$L$-distributive transformation.
Definition 2.4.13 By Proposition 2.1.5, an ![]() $L$-distributive functor
$L$-distributive functor ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}^{\Delta ^{1}}$ corresponds to a natural transformation
$\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}^{\Delta ^{1}}$ corresponds to a natural transformation
such that both ![]() $\eta _{0}$ and
$\eta _{0}$ and ![]() $\eta _{1}$ are
$\eta _{1}$ are ![]() $L$-distributive functors, and the mate square for the required left adjoints commutes. We call such a natural transformation an
$L$-distributive functors, and the mate square for the required left adjoints commutes. We call such a natural transformation an ![]() $L$-distributive transformation. We let
$L$-distributive transformation. We let ![]() ${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ denote the subcategory of
${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ denote the subcategory of ![]() ${\text {Fun}}(\operatorname {Span}_{F}(\mathcal {C}),\mathcal {X})$ consisting of
${\text {Fun}}(\operatorname {Span}_{F}(\mathcal {C}),\mathcal {X})$ consisting of ![]() $L$-distributive functors and
$L$-distributive functors and ![]() $L$-distributive transformations. From Proposition 2.1.5 we also know that a functor
$L$-distributive transformations. From Proposition 2.1.5 we also know that a functor ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}^{\mathsf {C}_{2}}$ is
$\operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}^{\mathsf {C}_{2}}$ is ![]() $L$-distributive if and only if its underlying functors and natural transformations to
$L$-distributive if and only if its underlying functors and natural transformations to ![]() $\mathcal {X}$ are
$\mathcal {X}$ are ![]() $L$-distributive, i.e. if and only if the adjoint morphism
$L$-distributive, i.e. if and only if the adjoint morphism
factors through ![]() ${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ on underlying
${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ on underlying ![]() $\infty$-categories. We therefore write
$\infty$-categories. We therefore write ![]() ${\text {FUN}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ for the locally full subcategory of
${\text {FUN}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ for the locally full subcategory of ![]() ${\text {FUN}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ whose underlying
${\text {FUN}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ whose underlying ![]() $\infty$-category is
$\infty$-category is ![]() ${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$.
${\text {Fun}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$.
Proposition 2.4.14 For any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {Y}$ there is a natural equivalence
$\mathcal {Y}$ there is a natural equivalence
Proof. We claim that the two sides are identified under the natural equivalence
Indeed, the subspace ![]() ${\text {Map}}_{{\text {Cat}}_{(\infty,2)}}(\mathcal {Y}, {\text {FUN}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X}))$ of the left-hand side consists of those functors
${\text {Map}}_{{\text {Cat}}_{(\infty,2)}}(\mathcal {Y}, {\text {FUN}}_{L{\text {-dist}}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X}))$ of the left-hand side consists of those functors ![]() $\Phi \colon \mathcal {Y} \to {\text {FUN}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ such that for every object
$\Phi \colon \mathcal {Y} \to {\text {FUN}}(\operatorname {Span}_{F}(\mathcal {C}), \mathcal {X})$ such that for every object ![]() $y \in \mathcal {Y}$ the image
$y \in \mathcal {Y}$ the image ![]() $\Phi (y)$ is an
$\Phi (y)$ is an ![]() $L$-distributive functor and for every morphism
$L$-distributive functor and for every morphism ![]() $f \colon y \to y'$ the image
$f \colon y \to y'$ the image ![]() $\Phi (f)$ is an
$\Phi (f)$ is an ![]() $L$-distributive natural transformation. Since the distributivity transformation is given pointwise by distributivity transformations in
$L$-distributive natural transformation. Since the distributivity transformation is given pointwise by distributivity transformations in ![]() $\mathcal {X}$, and equivalences in
$\mathcal {X}$, and equivalences in ![]() ${\text {FUN}}(\mathcal {Y}, \mathcal {X})$ are detected by evaluation at all objects of
${\text {FUN}}(\mathcal {Y}, \mathcal {X})$ are detected by evaluation at all objects of ![]() $\mathcal {Y}$, these conditions precisely correspond to
$\mathcal {Y}$, these conditions precisely correspond to ![]() $L$-distributivity for the adjoint functor
$L$-distributivity for the adjoint functor ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to {\text {FUN}}(\mathcal {Y}, \mathcal {X})$ by Proposition 2.1.5.
$\operatorname {Span}_{F}(\mathcal {C}) \to {\text {FUN}}(\mathcal {Y}, \mathcal {X})$ by Proposition 2.1.5.
2.5 The  $(\infty,2)$-category of bispans
$(\infty,2)$-category of bispans
Our goal in this subsection is to prove our main theorem.
Theorem 2.5.1 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple. Then there exists an
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple. Then there exists an ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ equipped with an
${\text {BISPAN}}_{F,L}(\mathcal {C})$ equipped with an ![]() $L$-distributive functor
$L$-distributive functor
such that:
(i) composition with
 $j$ gives an equivalence
for any
$j$ gives an equivalence
for any \[ {\text {FUN}}({\text {BISPAN}}_{F,L}(\mathcal{C}), \mathcal{X}) \xrightarrow{\sim} {\text {FUN}}_{L{\text {-dist}}}(\operatorname{Span}_{F}(\mathcal{C}), \mathcal{X}) \]
\[ {\text {FUN}}({\text {BISPAN}}_{F,L}(\mathcal{C}), \mathcal{X}) \xrightarrow{\sim} {\text {FUN}}_{L{\text {-dist}}}(\operatorname{Span}_{F}(\mathcal{C}), \mathcal{X}) \]
 $(\infty,2)$-category
$(\infty,2)$-category  $\mathcal {X}$;
$\mathcal {X}$;(ii) on underlying
 $\infty$-groupoids
$\infty$-groupoids  $j$ gives an equivalence
$j$ gives an equivalence
 \[ \mathcal{C}^{\simeq} \simeq \operatorname{Span}_{F}(\mathcal{C})^{\simeq} \xrightarrow{\sim} {\text {BISPAN}}_{F,L}(\mathcal{C})^{\simeq}; \]
\[ \mathcal{C}^{\simeq} \simeq \operatorname{Span}_{F}(\mathcal{C})^{\simeq} \xrightarrow{\sim} {\text {BISPAN}}_{F,L}(\mathcal{C})^{\simeq}; \]
(iii) morphisms in
 ${\text {BISPAN}}_{F,L}(\mathcal {C})$ are bispans
with
${\text {BISPAN}}_{F,L}(\mathcal {C})$ are bispans
with
 $f$ in
$f$ in  $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and  $l$ in
$l$ in  $\mathcal {C}_{L}$, with composition given by (5);
$\mathcal {C}_{L}$, with composition given by (5);(iv) 2-morphisms in
 ${\text {BISPAN}}_{F,L}(\mathcal {C})$ are given by diagrams of the form (6).
${\text {BISPAN}}_{F,L}(\mathcal {C})$ are given by diagrams of the form (6).
In order to prove this we will reinterpret the notion of distributivity as a special case of left adjointability, as follows.
Theorem 2.5.2 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair:
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair:
(1)
 $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple if and only if
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple if and only if  $(\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}},\mathcal {C}_{L})$ is a span pair;
$(\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}},\mathcal {C}_{L})$ is a span pair;(2) if case (1) holds, a functor
 $\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$ is
$\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$ is  $L$-distributive if and only if it is left
$L$-distributive if and only if it is left  $L$-adjointable.
$L$-adjointable.
Given this, the universal property we want is precisely that of the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {SPAN}_{L}(\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}})$; this amounts to interpreting a bispan as a ‘span in spans’:
$\operatorname {SPAN}_{L}(\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}})$; this amounts to interpreting a bispan as a ‘span in spans’:

The observation that the composition law for bispans can be interpreted as a pullback in spans is due to Street [Reference StreetStr20]. To prove this in our ![]() $\infty$-categorical setting we must first describe certain pullback squares in
$\infty$-categorical setting we must first describe certain pullback squares in ![]() $\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}}$.
$\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}}$.
Notation 2.5.3 Let us write ![]() $\operatorname {Sq}(\mathcal {C}) := {\text {Fun}}([1] \times [1], \mathcal {C})$ for the
$\operatorname {Sq}(\mathcal {C}) := {\text {Fun}}([1] \times [1], \mathcal {C})$ for the ![]() $\infty$-category of squares in an
$\infty$-category of squares in an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$, and given two morphisms
$\mathcal {C}$, and given two morphisms ![]() $f,g$ in
$f,g$ in ![]() $\mathcal {C}$ with common codomain we write
$\mathcal {C}$ with common codomain we write ![]() $\operatorname {Sq}_{f,g}(\mathcal {C})$ for the fibre of
$\operatorname {Sq}_{f,g}(\mathcal {C})$ for the fibre of ![]() $\operatorname {Sq}(\mathcal {C})$ at
$\operatorname {Sq}(\mathcal {C})$ at ![]() $(f,g) \in {\text {Fun}}(\Lambda ^{2}_{2}, \mathcal {C})$ (where we view
$(f,g) \in {\text {Fun}}(\Lambda ^{2}_{2}, \mathcal {C})$ (where we view ![]() $[1] \times [1]$ as
$[1] \times [1]$ as ![]() $(\Lambda ^{2}_{2})^{\triangleleft }$). Then a pullback of
$(\Lambda ^{2}_{2})^{\triangleleft }$). Then a pullback of ![]() $f$ and
$f$ and ![]() $g$ is precisely a terminal object in
$g$ is precisely a terminal object in ![]() $\operatorname {Sq}_{f,g}(\mathcal {C})$. Note also that evaluation at the initial object in
$\operatorname {Sq}_{f,g}(\mathcal {C})$. Note also that evaluation at the initial object in ![]() $[1] \times [1]$ gives a right fibration
$[1] \times [1]$ gives a right fibration ![]() $\operatorname {Sq}_{f,g}(\mathcal {C}) \to \mathcal {C}$.
$\operatorname {Sq}_{f,g}(\mathcal {C}) \to \mathcal {C}$.
Notation 2.5.4 We can identify ![]() $\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}}$ as the
$\operatorname {Span}_{F}(\mathcal {C})^{{\text {op}}}$ as the ![]() $\infty$-category of spans in
$\infty$-category of spans in ![]() $\mathcal {C}$ where the backwards map must lie in
$\mathcal {C}$ where the backwards map must lie in ![]() $\mathcal {C}_{F}$, with composition given by pullbacks in
$\mathcal {C}_{F}$, with composition given by pullbacks in ![]() $\mathcal {C}$ as usual. To emphasize this, we will use the notation
$\mathcal {C}$ as usual. To emphasize this, we will use the notation
For ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$, we then write
$\mathcal {C}_{F}$, we then write ![]() $[f]_{B}$ for the morphism
$[f]_{B}$ for the morphism ![]() $y \xleftarrow {f} x \xrightarrow {=} x$ in
$y \xleftarrow {f} x \xrightarrow {=} x$ in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, and for any
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, and for any ![]() $f$ in
$f$ in ![]() $\mathcal {C}$ we write
$\mathcal {C}$ we write ![]() $[f]_{F}$ for the span
$[f]_{F}$ for the span ![]() $x \xleftarrow {=} x \xrightarrow {f} y$.
$x \xleftarrow {=} x \xrightarrow {f} y$.
Remark 2.5.5 A square in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ can then be identified with a diagram of the shape
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ can then be identified with a diagram of the shape

where the two indicated squares are cartesian and the backwards maps all lie in ![]() $\mathcal {C}_{F}$. Composing this with a span (indicated by squiggly arrows) we get the diagram
$\mathcal {C}_{F}$. Composing this with a span (indicated by squiggly arrows) we get the diagram

which exhibits a cartesian morphism in ![]() $\operatorname {Sq}_{\phi,\psi }(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ where
$\operatorname {Sq}_{\phi,\psi }(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ where ![]() $\phi$ and
$\phi$ and ![]() $\psi$ are the bottom and right sides of the square.
$\psi$ are the bottom and right sides of the square.
Warning 2.5.6 To avoid cluttering the notation too much in the many diagrams that follow, throughout this section we will often abuse notation and denote as identities what should more correctly be arbitrary equivalences; the justification for this is that in each case we are really looking at a contractible space of diagrams that has the diagram with identities as one of its points.
Remark 2.5.7 As a special case of Remark 2.5.5, we can identify objects of ![]() $\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ with diagrams of the form
$\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ with diagrams of the form

where ![]() $\sigma$ is the bottom span. We can simplify this to
$\sigma$ is the bottom span. We can simplify this to

where the map ![]() $\phi$ is required to lie in
$\phi$ is required to lie in ![]() $\mathcal {C}_{F}$. Simplifying (24) similarly, we see that the cartesian morphism in
$\mathcal {C}_{F}$. Simplifying (24) similarly, we see that the cartesian morphism in ![]() $\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ over a span is given by a diagram of the form
$\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ over a span is given by a diagram of the form

where the squiggly arrows indicate the source object, the dashed arrows indicate the target object, and the double arrows indicate the span we compose with.
The following observation will be useful to describe both classes of pullbacks we are interested in.
Lemma 2.5.8 Suppose the diagram

is a terminal object in ![]() $\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, where
$\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, where ![]() $\sigma$ is the bottom span. Then
$\sigma$ is the bottom span. Then ![]() $\phi$ is an equivalence.
$\phi$ is an equivalence.
Proof. The diagram

is also an object of ![]() $\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, and so there exists a unique span
$\operatorname {Sq}_{\sigma,[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, and so there exists a unique span
with ![]() $\alpha$ in
$\alpha$ in ![]() $\mathcal {C}_{F}$, such that composing the terminal object with the span gives this object, i.e. we have a diagram
$\mathcal {C}_{F}$, such that composing the terminal object with the span gives this object, i.e. we have a diagram

But this means that if we compose the terminal object with the span ![]() $z \xleftarrow {\phi \alpha } u \xrightarrow {\beta } z$, then we get the terminal object back. Hence, by uniqueness this span must be equivalent to the identity span of
$z \xleftarrow {\phi \alpha } u \xrightarrow {\beta } z$, then we get the terminal object back. Hence, by uniqueness this span must be equivalent to the identity span of ![]() $z$. Thus, we may take
$z$. Thus, we may take ![]() $u = z$, and under this identification
$u = z$, and under this identification ![]() $\phi \alpha$ and
$\phi \alpha$ and ![]() $\beta$ are identified with
$\beta$ are identified with ![]() ${\text {id}}_{z}$. We may then identify the pullback
${\text {id}}_{z}$. We may then identify the pullback ![]() $\phi '$ with
$\phi '$ with ![]() $\phi$, so that we have
$\phi$, so that we have ![]() $\alpha \phi \simeq {\text {id}}_{y}$ as well as
$\alpha \phi \simeq {\text {id}}_{y}$ as well as ![]() $\phi \alpha \simeq {\text {id}}_{y}$. Thus,
$\phi \alpha \simeq {\text {id}}_{y}$. Thus, ![]() $\phi$ is indeed an equivalence.
$\phi$ is indeed an equivalence.
Remark 2.5.9 Specializing Remark 2.5.7 further, we can identify objects of
with diagrams of the form

which we can simplify to

where the top left arrow is required to lie in ![]() $\mathcal {C}_{F}$. Simplifying (26) similarly, we see that the cartesian morphism in
$\mathcal {C}_{F}$. Simplifying (26) similarly, we see that the cartesian morphism in ![]() $\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ over a span is given by a diagram of the form
$\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ over a span is given by a diagram of the form

where the squiggly arrows indicate the source object, the dashed arrows indicate the target object, and the double arrows indicate the span we compose with.
Proposition 2.5.10 Let ![]() $(\mathcal {C},\mathcal {C}_{F})$ be a span pair. Given morphisms
$(\mathcal {C},\mathcal {C}_{F})$ be a span pair. Given morphisms ![]() $f \colon a \to c$ and
$f \colon a \to c$ and ![]() $g \colon b \to c$ in
$g \colon b \to c$ in ![]() $\mathcal {C}$, the fibre product of
$\mathcal {C}$, the fibre product of ![]() $[f]_{F}$ and
$[f]_{F}$ and ![]() $[g]_{F}$ exists in
$[g]_{F}$ exists in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ if and only if the fibre product
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ if and only if the fibre product ![]() $d := a \times _{c}b$ of
$d := a \times _{c}b$ of ![]() $f$ and
$f$ and ![]() $g$ exists in
$g$ exists in ![]() $\mathcal {C}$, in which case it is given by the diagram
$\mathcal {C}$, in which case it is given by the diagram

Proof. By Lemma 2.5.8 we know that a terminal object of ![]() $\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, if it exists, must be of the form
$\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, if it exists, must be of the form

Now observe that composing (
29) with a span ![]() $z \xleftarrow {\alpha } y \xrightarrow {\beta } x$, we obtain the object
$z \xleftarrow {\alpha } y \xrightarrow {\beta } x$, we obtain the object

Thus, an object

of ![]() $\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ has a unique map to (
$\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ has a unique map to (
) if and only if there is a unique diagram

in ![]() $\mathcal {C}$. This is true for all objects of
$\mathcal {C}$. This is true for all objects of ![]() $\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ if and only if the square in (
$\operatorname {Sq}_{[f]_{F},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ if and only if the square in (
) is cartesian in ![]() $\mathcal {C}$, which is what we wanted to prove.
$\mathcal {C}$, which is what we wanted to prove.
Remark 2.5.11 Returning to Remark 2.5.7, an object of ![]() $\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ can be identified with a diagram
$\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ can be identified with a diagram

which we can simplify to

Composing this with a span gives, by simplifying (26), a diagram of the form

with the squiggly arrows indicating the source object, the dashed arrows the target object, and the double arrows the span we compose with.
Proposition 2.5.12 Let ![]() $(\mathcal {C},\mathcal {C}_{F})$ be a span pair. Given morphisms
$(\mathcal {C},\mathcal {C}_{F})$ be a span pair. Given morphisms ![]() $g \colon a \to b$ in
$g \colon a \to b$ in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $f \colon b \to c$ in
$f \colon b \to c$ in ![]() $\mathcal {C}_{F}$, the fibre product of
$\mathcal {C}_{F}$, the fibre product of ![]() $[f]_{B}$ and
$[f]_{B}$ and ![]() $[g]_{F}$ exists in
$[g]_{F}$ exists in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ if and only if there exists a distributivity diagram
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ if and only if there exists a distributivity diagram

in ![]() $\mathcal {C}$, in which case it is given by the diagram
$\mathcal {C}$, in which case it is given by the diagram

Proof. By Lemma 2.5.8, a terminal object of ![]() $\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, if it exists, must necessarily be of the form
$\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, if it exists, must necessarily be of the form

Composing this diagram with a span ![]() $y \xleftarrow {\beta } z \xrightarrow {\gamma } w$, we see from (28) that we get the outer part of the diagram
$y \xleftarrow {\beta } z \xrightarrow {\gamma } w$, we see from (28) that we get the outer part of the diagram

Thus, from Remark 2.4.2 we get that every object of ![]() $\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ admits a unique morphism to an object (
$\operatorname {Sq}_{[f]_{B},[g]_{F}}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ admits a unique morphism to an object (
) if and only if this is given by a distributivity diagram in ![]() $\mathcal {C}$, as required.
$\mathcal {C}$, as required.
Proof of Theorem 2.5.2 Every morphism in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ is a composite of morphisms of the form
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$ is a composite of morphisms of the form ![]() $[f]_{B}$ (with
$[f]_{B}$ (with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$) and
$\mathcal {C}_{F}$) and ![]() $[g]_{F}$. Thus,
$[g]_{F}$. Thus, ![]() $(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}), \mathcal {C}_{L})$ is a span pair if and only if for all
$(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}), \mathcal {C}_{L})$ is a span pair if and only if for all ![]() $l$ in
$l$ in ![]() $\mathcal {C}_{L}$ the pullbacks of
$\mathcal {C}_{L}$ the pullbacks of ![]() $[l]_{F}$ along
$[l]_{F}$ along ![]() $[g]_{F}$ and
$[g]_{F}$ and ![]() $[f]_{B}$ exist for all
$[f]_{B}$ exist for all ![]() $g$ in
$g$ in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$, and these pullbacks lie in
$\mathcal {C}_{F}$, and these pullbacks lie in ![]() $\mathcal {C}_{L}$. From Propositions 2.5.10 and 2.5.12 we see that these conditions are equivalent to
$\mathcal {C}_{L}$. From Propositions 2.5.10 and 2.5.12 we see that these conditions are equivalent to ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ being a bispan triple, which proves part (1). To prove part (2), observe that since adjointable squares compose, the functor
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ being a bispan triple, which proves part (1). To prove part (2), observe that since adjointable squares compose, the functor ![]() $\Phi$ is left
$\Phi$ is left ![]() $L$-adjointable if and only if we get left adjointable squares for both types of pullbacks along morphisms in
$L$-adjointable if and only if we get left adjointable squares for both types of pullbacks along morphisms in ![]() $\mathcal {C}_{L}$ separately. From Proposition 2.5.10 adjointability for the first type corresponds to
$\mathcal {C}_{L}$ separately. From Proposition 2.5.10 adjointability for the first type corresponds to ![]() $\Phi |_{\mathcal {C}^{{\text {op}}}}$ being left
$\Phi |_{\mathcal {C}^{{\text {op}}}}$ being left ![]() $L$-adjointable, and adjointability for the second type then corresponds to
$L$-adjointable, and adjointability for the second type then corresponds to ![]() $L$-distributivity by Remark 2.4.11.
$L$-distributivity by Remark 2.4.11.
Definition 2.5.13 In light of Theorem 2.5.2, if ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple it makes sense to define
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple it makes sense to define
Notation 2.5.14 In keeping with our conventions so far, we will denote the underlying ![]() $\infty$-category of
$\infty$-category of ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ by
${\text {BISPAN}}_{F,L}(\mathcal {C})$ by
In examples we will often have ![]() $\mathcal {C}_{L} \simeq \mathcal {C}$, in which case we abbreviate
$\mathcal {C}_{L} \simeq \mathcal {C}$, in which case we abbreviate ![]() ${\text {BISPAN}}_{F}(\mathcal {C}) := {\text {BISPAN}}_{F,L}(\mathcal {C})$. If we also have
${\text {BISPAN}}_{F}(\mathcal {C}) := {\text {BISPAN}}_{F,L}(\mathcal {C})$. If we also have ![]() $\mathcal {C}_{F} \simeq \mathcal {C}$, we write
$\mathcal {C}_{F} \simeq \mathcal {C}$, we write ![]() ${\text {BISPAN}}(\mathcal {C})$ for
${\text {BISPAN}}(\mathcal {C})$ for ![]() ${\text {BISPAN}}_{F}(\mathcal {C})$. We also adopt the same conventions for the
${\text {BISPAN}}_{F}(\mathcal {C})$. We also adopt the same conventions for the ![]() $\infty$-category of bispans
$\infty$-category of bispans ![]() ${\text {Bispan}}_{F,L}(\mathcal {C})$.
${\text {Bispan}}_{F,L}(\mathcal {C})$.
Applying Corollary 2.3.5, we obtain the following result.
Corollary 2.5.15 Let ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple. The
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple. The ![]() $\infty$-category
$\infty$-category ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ satisfies
${\text {BISPAN}}_{F,L}(\mathcal {C})$ satisfies
for any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$.
$\mathcal {X}$.
This proves part (i) of Theorem 2.5.1. We now prove the remainder.
Proof of Theorem 2.5.1 Part (ii) is immediate from Corollary 2.3.21. A morphism in ![]() $\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ is a ‘span of spans’
$\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$ is a ‘span of spans’

with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $l$ in
$l$ in ![]() $\mathcal {C}_{L}$, which we can think of as a bispan by contracting the identity. To compose these we take pullbacks in
$\mathcal {C}_{L}$, which we can think of as a bispan by contracting the identity. To compose these we take pullbacks in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, which we can unpack to give the expected composition law for bispans using Propositions 2.5.10 and 2.5.12. Unpacking the definition of a 2-morphism in
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, which we can unpack to give the expected composition law for bispans using Propositions 2.5.10 and 2.5.12. Unpacking the definition of a 2-morphism in ![]() $\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, we get a diagram
$\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C}))$, we get a diagram

where the upward-pointing map is necessarily an equivalence, as indicated. Contracting the invertible edges, we get a diagram of shape (6), as required.
The universal property also implies that our ![]() $(\infty,2)$-categories of bispans are functorial for morphisms of bispan triples, in the following sense.
$(\infty,2)$-categories of bispans are functorial for morphisms of bispan triples, in the following sense.
Definition 2.5.16 A morphism of bispan triples ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L}) \to (\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ is a functor
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L}) \to (\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ is a functor ![]() $\phi \colon \mathcal {C} \to \mathcal {C}'$ such that
$\phi \colon \mathcal {C} \to \mathcal {C}'$ such that ![]() $\phi (\mathcal {C}_{F}) \subseteq \mathcal {C}'_{F'}$,
$\phi (\mathcal {C}_{F}) \subseteq \mathcal {C}'_{F'}$, ![]() $\phi (\mathcal {C}_{L}) \subseteq \mathcal {C}'_{L'}$, and
$\phi (\mathcal {C}_{L}) \subseteq \mathcal {C}'_{L'}$, and ![]() $\phi$ preserves pullbacks along
$\phi$ preserves pullbacks along ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $\mathcal {C}_{L}$ as well as distributivity diagrams. We define
$\mathcal {C}_{L}$ as well as distributivity diagrams. We define ![]() ${\text {Trip}}$ to be the subcategory of
${\text {Trip}}$ to be the subcategory of ![]() ${\text {Fun}}(\Lambda ^{2}_{2}, {\text {Cat}}_\infty )$ containing the bispan triples and the morphisms thereof.
${\text {Fun}}(\Lambda ^{2}_{2}, {\text {Cat}}_\infty )$ containing the bispan triples and the morphisms thereof.
Proposition 2.5.17 There is a functor ![]() ${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$ that takes
${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$ that takes ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ to
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ to ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$.
${\text {BISPAN}}_{F,L}(\mathcal {C})$.
Proof. Composition with a morphism of bispan triples ![]() $\phi \colon (\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L}) \to (\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ restricts for any
$\phi \colon (\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L}) \to (\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ restricts for any ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\mathcal {X}$ to a morphism
$\mathcal {X}$ to a morphism
so we get a functor
By Theorem 2.5.1 the associated functor ![]() ${\text {Trip}}^{{\text {op}}} \to {\text {Fun}}({\text {Cat}}_{(\infty,2)}, \mathcal {S})$ factors through the full subcategory of corepresentable copresheaves, and so by the Yoneda lemma arises from a functor
${\text {Trip}}^{{\text {op}}} \to {\text {Fun}}({\text {Cat}}_{(\infty,2)}, \mathcal {S})$ factors through the full subcategory of corepresentable copresheaves, and so by the Yoneda lemma arises from a functor ![]() ${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$, as required.
${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$, as required.
Applying Proposition 2.3.23 to ![]() $\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, we obtain the following description of the functor of
$\operatorname {SPAN}_{L}(\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$, we obtain the following description of the functor of ![]() $(\infty,2)$-categories corresponding to a distributive functor.
$(\infty,2)$-categories corresponding to a distributive functor.
Corollary 2.5.18 For an ![]() $L$-distributive functor
$L$-distributive functor ![]() $\phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$, the corresponding functor
$\phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to \mathcal {X}$, the corresponding functor ![]() $\Phi \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to \mathcal {X}$ can be described as follows.
$\Phi \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to \mathcal {X}$ can be described as follows.
(1) On objects,
 $\Phi (c) \simeq \phi (c)$ for
$\Phi (c) \simeq \phi (c)$ for  $c \in \mathcal {C}$.
$c \in \mathcal {C}$.(2) On morphisms,
 $\Phi$ takes a bispan
to the composite
$\Phi$ takes a bispan
to the composite \[ B = (x \xleftarrow{s} e \xrightarrow{f} b \xrightarrow{l} y) \]
\[ B = (x \xleftarrow{s} e \xrightarrow{f} b \xrightarrow{l} y) \]
 $l_{\oplus }f_{\otimes }s^{\circledast } \colon \phi (x) \to \phi (y)$, where
$l_{\oplus }f_{\otimes }s^{\circledast } \colon \phi (x) \to \phi (y)$, where  $l_{\oplus }$ is the left adjoint to
$l_{\oplus }$ is the left adjoint to  $l^{\circledast }$.
$l^{\circledast }$.(3) On 2-morphisms,
 $\Phi$ takes the 2-morphism
$\Phi$ takes the 2-morphism  $\beta \colon B \to B'$ given by the commutative diagram
to the composite
$\beta \colon B \to B'$ given by the commutative diagram
to the composite where the first noninvertible arrow is a unit and the second noninvertible arrow is a counit.
where the first noninvertible arrow is a unit and the second noninvertible arrow is a counit. \[ l_{\oplus}f_{\otimes}s^{\circledast} \simeq l_{\oplus}f_{\otimes}g^{\circledast}s'^{\circledast} \simeq l_{\oplus}h^{\circledast}f'_{\otimes}s'^{\circledast} \to l_{\oplus}h^{\circledast}l'^{\circledast}l'_{\oplus}f'_{\otimes}s'^{\circledast} \simeq l_{\oplus}l^{\circledast}l'_{\oplus}f'_{\otimes}s'^{\circledast} \to l'_{\oplus}f'_{\otimes}s'^{\circledast}, \]
\[ l_{\oplus}f_{\otimes}s^{\circledast} \simeq l_{\oplus}f_{\otimes}g^{\circledast}s'^{\circledast} \simeq l_{\oplus}h^{\circledast}f'_{\otimes}s'^{\circledast} \to l_{\oplus}h^{\circledast}l'^{\circledast}l'_{\oplus}f'_{\otimes}s'^{\circledast} \simeq l_{\oplus}l^{\circledast}l'_{\oplus}f'_{\otimes}s'^{\circledast} \to l'_{\oplus}f'_{\otimes}s'^{\circledast}, \]
We end this section with some useful observations about distributivity diagrams that follow easily from Proposition 2.5.12.
Lemma 2.5.19 Let ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose given morphisms
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose given morphisms ![]() $l_{1} \colon x\to y$ and
$l_{1} \colon x\to y$ and ![]() $l_{2} \colon y \to z$ in
$l_{2} \colon y \to z$ in ![]() $L$ and
$L$ and ![]() $f \colon z \to w$ in
$f \colon z \to w$ in ![]() $F$. Then we can make the following diagram:
$F$. Then we can make the following diagram:

Here all three squares are cartesian and the two rightmost give distributivity diagrams (so ![]() $g_{2} = f_{*}l_{2}$,
$g_{2} = f_{*}l_{2}$, ![]() $g_{1} = f'_{*}l_{1}'$). Then the outer diagram is a distributivity diagram for
$g_{1} = f'_{*}l_{1}'$). Then the outer diagram is a distributivity diagram for ![]() $l_{2}l_{1}$ and
$l_{2}l_{1}$ and ![]() $f$.
$f$.
Proof. This follows immediately from the pasting lemma for pullback squares applied to ![]() $[l_{2}l_{1}]_{F} \simeq [l_{2}]_{F}\circ [l_{1}]_{F}$ and
$[l_{2}l_{1}]_{F} \simeq [l_{2}]_{F}\circ [l_{1}]_{F}$ and ![]() $[f]_{B}$ in
$[f]_{B}$ in ![]() $\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$.
$\operatorname {Span}_{F,{\text {all}}}(\mathcal {C})$.
Lemma 2.5.20 Let ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose given morphisms
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose given morphisms ![]() $l \colon x\to y$ in
$l \colon x\to y$ in ![]() $L$ and
$L$ and ![]() $f_{1} \colon y \to z, f_{2} \colon z \to w$ in
$f_{1} \colon y \to z, f_{2} \colon z \to w$ in ![]() $F$. Then we can make the following diagram:
$F$. Then we can make the following diagram:

Here all three squares are cartesian and two give distributivity diagrams (exhibiting ![]() $g_{1} = f_{1,*}l$ and
$g_{1} = f_{1,*}l$ and ![]() $g_{2} = f_{2,*}g_{1}$. Then the outer diagram is a distributivity diagram for
$g_{2} = f_{2,*}g_{1}$. Then the outer diagram is a distributivity diagram for ![]() $l$ and
$l$ and ![]() $f_{2}f_{1}$. (Note that the composite square is indeed cartesian since the two left squares are cartesian and the middle triangle just exhibits
$f_{2}f_{1}$. (Note that the composite square is indeed cartesian since the two left squares are cartesian and the middle triangle just exhibits ![]() $g_{2}'$ as a composite.)
$g_{2}'$ as a composite.)
Proof. This is the pasting lemma for pullback squares applied to ![]() $[f_{2}f_{1}]_{B} \simeq [f_{1}]_{B}\circ [f_{2}]_{B}$ and
$[f_{2}f_{1}]_{B} \simeq [f_{1}]_{B}\circ [f_{2}]_{B}$ and ![]() $[l]_{F}$.
$[l]_{F}$.
Lemma 2.5.21 Let ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose we have morphisms
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose we have morphisms ![]() $l \colon x \to y$ in
$l \colon x \to y$ in ![]() $\mathcal {C}_{L}$,
$\mathcal {C}_{L}$, ![]() $f \colon y \to z$ in
$f \colon y \to z$ in ![]() $\mathcal {C}_{F}$ and an arbitrary morphism
$\mathcal {C}_{F}$ and an arbitrary morphism ![]() $\zeta \colon z' \to z$. Then we can form the diagram
$\zeta \colon z' \to z$. Then we can form the diagram

where the front face is a distributivity diagram for ![]() $l$ and
$l$ and ![]() $f$, and the rest of the diagram is obtained by pulling this back along
$f$, and the rest of the diagram is obtained by pulling this back along ![]() $\zeta$. Then the back face in (35) is a distributivity diagram for
$\zeta$. Then the back face in (35) is a distributivity diagram for ![]() $l'$ and
$l'$ and ![]() $f'$.
$f'$.
Proof. This follows yet again from the pasting lemma for pullback squares, now applied to the pullback of ![]() $[l]_{F}$ along
$[l]_{F}$ along ![]() $[f]_{B}\circ [\zeta ]_{F} \simeq [\eta ]_{F} \circ [f']_{B}$.
$[f]_{B}\circ [\zeta ]_{F} \simeq [\eta ]_{F} \circ [f']_{B}$.
The following proposition can be interpreted as saying that distributivity transformations are compatible with base change.
Proposition 2.5.22 Let ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose we have the diagram (35). Then the distributivity transformations for
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ be a bispan triple, and suppose we have the diagram (35). Then the distributivity transformations for ![]() $(l,f)$ and
$(l,f)$ and ![]() $(l',f')$ are related by a commutative square of the form
$(l',f')$ are related by a commutative square of the form

Proof. We have the following commutative cube:

This means the following pair of diagrams are identified under the equivalences ![]() $f'_{\otimes }\eta ^{\circledast } \simeq \zeta ^{\circledast }f_{\otimes }$,
$f'_{\otimes }\eta ^{\circledast } \simeq \zeta ^{\circledast }f_{\otimes }$, ![]() $h'_{\otimes }\epsilon '^{\circledast }\xi ^{\circledast } \simeq \omega ^{\circledast }h_{\otimes }\epsilon ^{\circledast }$ given by the left and right faces of the cube:
$h'_{\otimes }\epsilon '^{\circledast }\xi ^{\circledast } \simeq \omega ^{\circledast }h_{\otimes }\epsilon ^{\circledast }$ given by the left and right faces of the cube:

We get a corresponding identification of the mates of the outer squares in these two diagrams, which, in turn, decompose (since mate transformations are compatible with vertical pasting of squares) into the mates of the two smaller squares; according to Remark 2.4.11 these are the base change transformation ![]() $g'_{\oplus }\omega ^{\circledast } \to \zeta ^{\circledast }g_{\oplus }$ and the distributivity transformation for
$g'_{\oplus }\omega ^{\circledast } \to \zeta ^{\circledast }g_{\oplus }$ and the distributivity transformation for ![]() $(l,f)$ on the left, and the distributivity transformation for
$(l,f)$ on the left, and the distributivity transformation for ![]() $(l',f')$ and the base change transformation
$(l',f')$ and the base change transformation ![]() $l'_{\oplus }\xi ^{\circledast } \to \eta ^{\circledast }l_{\oplus }$ on the right. This identification gives precisely a commutative diagram
$l'_{\oplus }\xi ^{\circledast } \to \eta ^{\circledast }l_{\oplus }$ on the right. This identification gives precisely a commutative diagram

which we can reorganize into the commutative diagram in the statement.
2.6 Symmetric monoidal structures
In this subsection we will prove that the functor ![]() $\operatorname {SPAN} \colon {\text {Pair}} \to {\text {Cat}}_{(\infty,2)}$ preserves products. Applying this in the special case of bispans, we will see that in some cases a symmetric monoidal structure on
$\operatorname {SPAN} \colon {\text {Pair}} \to {\text {Cat}}_{(\infty,2)}$ preserves products. Applying this in the special case of bispans, we will see that in some cases a symmetric monoidal structure on ![]() $\mathcal {C}$ induces a symmetric monoidal structure on
$\mathcal {C}$ induces a symmetric monoidal structure on ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$, and also show that
${\text {BISPAN}}_{F,L}(\mathcal {C})$, and also show that ![]() ${\text {BISPAN}}(-)$ is a functor of
${\text {BISPAN}}(-)$ is a functor of ![]() $(\infty,2)$-categories. The construction of symmetric monoidal structures on spans is also discussed in [Reference Gaitsgory and RozenblyumGR17, Part III, Chapter 9] (where it is used to encode Serre duality for Ind-coherent sheaves) and [Reference MacphersonMac22, § 3.2]. An explicit construction (not relying on the universal property) of symmetric monoidal structures on
$(\infty,2)$-categories. The construction of symmetric monoidal structures on spans is also discussed in [Reference Gaitsgory and RozenblyumGR17, Part III, Chapter 9] (where it is used to encode Serre duality for Ind-coherent sheaves) and [Reference MacphersonMac22, § 3.2]. An explicit construction (not relying on the universal property) of symmetric monoidal structures on ![]() $\infty$-categories of spans is also given in [Reference Barwick, Glasman and ShahBGS20].
$\infty$-categories of spans is also given in [Reference Barwick, Glasman and ShahBGS20].
Proposition 2.6.1 The ![]() $\infty$-categories
$\infty$-categories ![]() ${\text {Pair}}$ and
${\text {Pair}}$ and ![]() ${\text {Trip}}$ have finite products, given by
${\text {Trip}}$ have finite products, given by
Proof. It follows from the definition of ![]() ${\text {Pair}}$ that the morphism
${\text {Pair}}$ that the morphism
is a monomorphism (and similarly for ![]() ${\text {Trip}}$), so it suffices to show that for any span pair
${\text {Trip}}$), so it suffices to show that for any span pair ![]() $(\mathcal {D}, \mathcal {D}_{F})$ (or bispan triple
$(\mathcal {D}, \mathcal {D}_{F})$ (or bispan triple ![]() $(\mathcal {D}, \mathcal {D}_{F}, \mathcal {D}_{L})$) a functor
$(\mathcal {D}, \mathcal {D}_{F}, \mathcal {D}_{L})$) a functor ![]() $\mathcal {D} \to \mathcal {C} \times \mathcal {C}'$ is a morphism of span pairs (or bispan triples) if and only if the functors
$\mathcal {D} \to \mathcal {C} \times \mathcal {C}'$ is a morphism of span pairs (or bispan triples) if and only if the functors ![]() $\mathcal {D} \to \mathcal {C}$ and
$\mathcal {D} \to \mathcal {C}$ and ![]() $\mathcal {D} \to \mathcal {C}'$ are both morphisms of span pairs (or bispan triples). This is clear, since a pair of cartesian squares in
$\mathcal {D} \to \mathcal {C}'$ are both morphisms of span pairs (or bispan triples). This is clear, since a pair of cartesian squares in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {C}'$ gives a cartesian square in
$\mathcal {C}'$ gives a cartesian square in ![]() $\mathcal {C} \times \mathcal {C}'$ and vice versa, and similarly for distributivity diagrams.
$\mathcal {C} \times \mathcal {C}'$ and vice versa, and similarly for distributivity diagrams.
Proposition 2.6.2 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F})$ and
$(\mathcal {C},\mathcal {C}_{F})$ and ![]() $(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then a functor
$(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then a functor ![]() $\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ is left
$\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ is left ![]() $(F,F')$-adjointable if and only if it is left adjointable in each variable, that is:
$(F,F')$-adjointable if and only if it is left adjointable in each variable, that is:
• for every
 $c \in \mathcal {C}$, the functor
$c \in \mathcal {C}$, the functor  $\Phi (c,-)$ is left
$\Phi (c,-)$ is left  $F'$-adjointable;
$F'$-adjointable;• for every
 $c' \in \mathcal {C}'$, the functor
$c' \in \mathcal {C}'$, the functor  $\Phi (-,c')$ is left
$\Phi (-,c')$ is left  $F$-adjointable;
$F$-adjointable;• for every morphism
 $c_{1} \to c_{2}$ in
$c_{1} \to c_{2}$ in  $\mathcal {C}$, the transformation
$\mathcal {C}$, the transformation  $\Phi (c_{2},-) \to \Phi (c_{1},-)$ is left
$\Phi (c_{2},-) \to \Phi (c_{1},-)$ is left  $F'$-adjointable;
$F'$-adjointable;• for every morphism
 $c'_{1} \to c'_{2}$ in
$c'_{1} \to c'_{2}$ in  $\mathcal {C}'$, the transformation
$\mathcal {C}'$, the transformation  $\Phi (-, c'_{2}) \to \Phi (-, c'_{1})$ is left
$\Phi (-, c'_{2}) \to \Phi (-, c'_{1})$ is left  $F$-adjointable.
$F$-adjointable.
Proof. We first observe that ![]() $\Phi$ is left
$\Phi$ is left ![]() $(F,F')$-preadjointable if and only if
$(F,F')$-preadjointable if and only if ![]() $(f,{\text {id}}_{c'})^{\circledast }$ has a left adjoint for all
$(f,{\text {id}}_{c'})^{\circledast }$ has a left adjoint for all ![]() $f$ in
$f$ in ![]() $F$ and
$F$ and ![]() $c'$ in
$c'$ in ![]() $\mathcal {C}'$, and
$\mathcal {C}'$, and ![]() $({\text {id}}_{c}, f')^{\circledast }$ has a left adjoint for all
$({\text {id}}_{c}, f')^{\circledast }$ has a left adjoint for all ![]() $c$ in
$c$ in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $f'$ in
$f'$ in ![]() $F'$, since
$F'$, since ![]() $(f,f')^{\circledast } \simeq (f,{\text {id}})^{\circledast }({\text {id}},f')^{\circledast }$ and left adjoints compose. Thus,
$(f,f')^{\circledast } \simeq (f,{\text {id}})^{\circledast }({\text {id}},f')^{\circledast }$ and left adjoints compose. Thus, ![]() $\Phi$ is left
$\Phi$ is left ![]() $(F,F')$-preadjointable if and only if
$(F,F')$-preadjointable if and only if ![]() $\Phi (c,-)$ is left
$\Phi (c,-)$ is left ![]() $F'$-preadjointable for all
$F'$-preadjointable for all ![]() $c \in \mathcal {C}$ and
$c \in \mathcal {C}$ and ![]() $\Phi (-,c')$ is left
$\Phi (-,c')$ is left ![]() $F$-preadjointable for all
$F$-preadjointable for all ![]() $c'$ in
$c'$ in ![]() $\mathcal {C}'$.
$\mathcal {C}'$.
A pair of cartesian squares gives a cartesian square in ![]() $\mathcal {C} \times \mathcal {C}'$, so if
$\mathcal {C} \times \mathcal {C}'$, so if ![]() $\Phi$ is left
$\Phi$ is left ![]() $(F,F')$-preadjointable then it is left
$(F,F')$-preadjointable then it is left ![]() $(F,F')$-adjointable if and only if for cartesian squares
$(F,F')$-adjointable if and only if for cartesian squares

with ![]() $f$ in
$f$ in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $f'$ in
$f'$ in ![]() $\mathcal {C}'_{F'}$, the square
$\mathcal {C}'_{F'}$, the square

is left adjointable. Taking ![]() $f = g = {\text {id}}_{c}$ this implies that
$f = g = {\text {id}}_{c}$ this implies that ![]() $\Phi (c,-)$ is left
$\Phi (c,-)$ is left ![]() $F'$-adjointable, while taking
$F'$-adjointable, while taking ![]() $f' = {\text {id}}_{y'}$ and
$f' = {\text {id}}_{y'}$ and ![]() $f = {\text {id}}_{y}$ we see that the transformation
$f = {\text {id}}_{y}$ we see that the transformation ![]() $\Phi (g,-) \colon \Phi (y,-) \to \Phi (z,-)$ is left
$\Phi (g,-) \colon \Phi (y,-) \to \Phi (z,-)$ is left ![]() $F'$-adjointable. The same goes in the other variable, so if
$F'$-adjointable. The same goes in the other variable, so if ![]() $\Phi$ is left
$\Phi$ is left ![]() $(F,F')$-adjointable, then the four given conditions hold.
$(F,F')$-adjointable, then the four given conditions hold.
Conversely, if these conditions hold, then we want to show that the square (37) is left adjointable. We can decompose this square into the following commutative diagram:

Here all four squares are left adjointable:
• the top left square since
 $\Phi (-,y')$ is left
$\Phi (-,y')$ is left  $F$-adjointable;
$F$-adjointable;• the top right square since
 $\Phi (u,-)$ is a left
$\Phi (u,-)$ is a left  $F'$-adjointable transformation;
$F'$-adjointable transformation;• the bottom left square since
 $\Phi (-,g')$ is a left
$\Phi (-,g')$ is a left  $F$-adjointable transformation;
$F$-adjointable transformation;• the bottom right square since
 $\Phi (w,-)$ is left
$\Phi (w,-)$ is left  $F'$-adjointable.
$F'$-adjointable.
Since mate transformations are compatible with horizontal and vertical compositions of squares, left adjointable squares are closed under both horizontal and vertical compositions. Thus, the outer square (37) is left adjointable, which completes the proof.
Corollary 2.6.3 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F})$ and
$(\mathcal {C},\mathcal {C}_{F})$ and ![]() $(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then there is a natural equivalence
$(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then there is a natural equivalence
for ![]() $\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$.
$\mathcal {X} \in {\text {Cat}}_{(\infty,2)}$.
To prove this we also need the following lemma.
Lemma 2.6.4 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair. A morphism
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair. A morphism ![]() $\eta \colon \phi \to \psi$ in the
$\eta \colon \phi \to \psi$ in the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ has a left adjoint if and only if:
${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ has a left adjoint if and only if:
(1) the morphism
 $\eta _{c} \colon \phi (c) \to \psi (c)$ has a left adjoint in
$\eta _{c} \colon \phi (c) \to \psi (c)$ has a left adjoint in  $\mathcal {X}$ for every
$\mathcal {X}$ for every  $c \in \mathcal {C}$;
$c \in \mathcal {C}$;(2) the commutative square

is left adjointable for every morphism ![]() $c \to c'$ in
$c \to c'$ in ![]() $\mathcal {C}$. Moreover, a commutative square
$\mathcal {C}$. Moreover, a commutative square

in ![]() ${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ is left adjointable if and only if the commutative square in
${\text {FUN}}_{F{\text {-ladj}}}(\mathcal {C}^{{\text {op}}}, \mathcal {X})$ is left adjointable if and only if the commutative square in ![]() $\mathcal {X}$ obtained by evaluation at
$\mathcal {X}$ obtained by evaluation at ![]() $c$ is left adjointable in
$c$ is left adjointable in ![]() $\mathcal {X}$ for every
$\mathcal {X}$ for every ![]() $c \in \mathcal {C}$.
$c \in \mathcal {C}$.
Proof. By Corollary 2.3.5 we have an equivalence
Suppose ![]() $H \colon \Phi \to \Psi$ is the morphism corresponding to
$H \colon \Phi \to \Psi$ is the morphism corresponding to ![]() $\eta \colon \phi \to \psi$ under this equivalence. Then we know that
$\eta \colon \phi \to \psi$ under this equivalence. Then we know that ![]() $H$ has a left adjoint if and only if:
$H$ has a left adjoint if and only if:
•
 $H_{c} \colon \Phi (c) \to \Psi (c)$ has a left adjoint for every
$H_{c} \colon \Phi (c) \to \Psi (c)$ has a left adjoint for every  $c \in \mathcal {C}$;
$c \in \mathcal {C}$;• the square

is left adjointable for every morphism ![]() $c_{1} \to c_{2}$ in
$c_{1} \to c_{2}$ in ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$. In terms of
$\operatorname {SPAN}_{F}(\mathcal {C})$. In terms of ![]() $\eta$, these conditions say that
$\eta$, these conditions say that ![]() $\eta _{c}$ has a left adjoint for every
$\eta _{c}$ has a left adjoint for every ![]() $c \in \mathcal {C}$, and for every span
$c \in \mathcal {C}$, and for every span ![]() $c_{1} \xleftarrow {g} x \xrightarrow {f} c_{2}$ with
$c_{1} \xleftarrow {g} x \xrightarrow {f} c_{2}$ with ![]() $f$ in
$f$ in ![]() $F$, the outer square in the diagram
$F$, the outer square in the diagram

is left adjointable. Since left adjointable squares compose, and the two squares here are those associated to spans where one leg is the identity, it is equivalent to require these two squares to be left adjointable. For the top square this is the condition we want, while the bottom square is automatically left adjointable since its mate is obtained by passing to left adjoints everywhere in the commutative square

Since the mate of a square of natural transformations is given by taking mates objectwise, the characterization of left adjointable squares is immediate.
Proof of Corollary 2.6.3 Unpacking definitions, a functor ![]() $\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ corresponds to a functor
$\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ corresponds to a functor ![]() $\mathcal {C}^{{\text {op}}} \to {\text {Fun}}_{F'{\text {-ladj}}}(\mathcal {C}'^{{\text {op}}}, \mathcal {X})$ if and only if
$\mathcal {C}^{{\text {op}}} \to {\text {Fun}}_{F'{\text {-ladj}}}(\mathcal {C}'^{{\text {op}}}, \mathcal {X})$ if and only if ![]() $\Phi (c,-)$ is a left
$\Phi (c,-)$ is a left ![]() $F'$-adjointable functor for every
$F'$-adjointable functor for every ![]() $c \in \mathcal {C}$, and
$c \in \mathcal {C}$, and ![]() $\Phi (c_{2},-) \to \Phi (c_{1},-)$ is a left
$\Phi (c_{2},-) \to \Phi (c_{1},-)$ is a left ![]() $F'$-adjointable transformation for every morphism
$F'$-adjointable transformation for every morphism ![]() $c_{1} \to c_{2}$ in
$c_{1} \to c_{2}$ in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Moreover, it follows from Lemma 2.6.4 that such a functor
is left ![]() $F$-adjointable precisely when the following conditions hold:
$F$-adjointable precisely when the following conditions hold:
• for every morphism
 $f\colon c_{1} \to c_{2}$ in
$f\colon c_{1} \to c_{2}$ in  $F$ and every object
$F$ and every object  $c' \in \mathcal {C}'$, the morphism
$c' \in \mathcal {C}'$, the morphism  $(f,{\text {id}})^{\circledast } \colon \Phi (c_{2},c') \to \Phi (c_{1},c')$ has a left adjoint;
$(f,{\text {id}})^{\circledast } \colon \Phi (c_{2},c') \to \Phi (c_{1},c')$ has a left adjoint;• for every morphism
 $f\colon c_{1} \to c_{2}$ in
$f\colon c_{1} \to c_{2}$ in  $F$ and every morphism
$F$ and every morphism  $c'_{1} \to c'_{2}$ in
$c'_{1} \to c'_{2}$ in  $\mathcal {C}'$, the commutative square
is left adjointable;
$\mathcal {C}'$, the commutative square
is left adjointable;
• for every pullback square
in
 $\mathcal {C}$ with
$\mathcal {C}$ with  $f$ in
$f$ in  $F$, the commutative square
is left adjointable.
$F$, the commutative square
is left adjointable.
These conditions say precisely that ![]() $\Phi (-,c')$ is a left
$\Phi (-,c')$ is a left ![]() $F$-adjointable functor for every
$F$-adjointable functor for every ![]() $c' \in \mathcal {C}'$ and
$c' \in \mathcal {C}'$ and ![]() $\Phi (-,c'_{2}) \to \Phi (-,c'_{1})$ is a left
$\Phi (-,c'_{2}) \to \Phi (-,c'_{1})$ is a left ![]() $F$-adjointable transformation for every morphism
$F$-adjointable transformation for every morphism ![]() $c'_{1} \to c'_{2}$ in
$c'_{1} \to c'_{2}$ in ![]() $\mathcal {C}'$. We have thus shown that a functor
$\mathcal {C}'$. We have thus shown that a functor ![]() $\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ corresponds to a left
$\Phi \colon \mathcal {C}^{{\text {op}}} \times \mathcal {C}'^{{\text {op}}} \to \mathcal {X}$ corresponds to a left ![]() $F$-adjointable functor
$F$-adjointable functor ![]() $\mathcal {C}^{{\text {op}}} \to {\text {Fun}}_{F'{\text {-ladj}}}(\mathcal {C}'^{{\text {op}}}, \mathcal {X})$ if and only if it satisfies the four conditions that we saw characterized left
$\mathcal {C}^{{\text {op}}} \to {\text {Fun}}_{F'{\text {-ladj}}}(\mathcal {C}'^{{\text {op}}}, \mathcal {X})$ if and only if it satisfies the four conditions that we saw characterized left ![]() $(F,F')$-adjointable functors in Proposition 2.6.2.
$(F,F')$-adjointable functors in Proposition 2.6.2.
From Corollary 2.6.3 we can now deduce that spans preserve products.
Corollary 2.6.5 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F})$ and
$(\mathcal {C},\mathcal {C}_{F})$ and ![]() $(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then the natural morphism
$(\mathcal {C}', \mathcal {C}'_{F'})$ are span pairs. Then the natural morphism
is an equivalence.
Proof. For ![]() $\mathcal {X}$ an
$\mathcal {X}$ an ![]() $(\infty,2)$-category we have natural equivalences
$(\infty,2)$-category we have natural equivalences
 \begin{align*} {\text {Map}}(\operatorname{SPAN}_{(F,F')}(\mathcal{C} \times \mathcal{C}'), \mathcal{X}) & \simeq {\text {Map}}_{(F,F'){\text {-ladj}}}(\mathcal{C}^{{\text {op}}} \times \mathcal{C}'^{{\text {op}}}, \mathcal{X})\\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}_{F'{\text {-ladj}}}(\mathcal{C}'^{{\text {op}}}, \mathcal{X})) \\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}(\operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X})) \\ & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}), {\text {FUN}}(\operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X})) \\ & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}) \times \operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X}). \end{align*}
\begin{align*} {\text {Map}}(\operatorname{SPAN}_{(F,F')}(\mathcal{C} \times \mathcal{C}'), \mathcal{X}) & \simeq {\text {Map}}_{(F,F'){\text {-ladj}}}(\mathcal{C}^{{\text {op}}} \times \mathcal{C}'^{{\text {op}}}, \mathcal{X})\\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}_{F'{\text {-ladj}}}(\mathcal{C}'^{{\text {op}}}, \mathcal{X})) \\ & \simeq {\text {Map}}_{F{\text {-ladj}}}(\mathcal{C}^{{\text {op}}}, {\text {FUN}}(\operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X})) \\ & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}), {\text {FUN}}(\operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X})) \\ & \simeq {\text {Map}}(\operatorname{SPAN}_{F}(\mathcal{C}) \times \operatorname{SPAN}_{F'}(\mathcal{C}'), \mathcal{X}). \end{align*}
Corollary 2.6.6 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair and
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair and ![]() $\mathcal {C}$ has a (symmetric) monoidal structure such that the tensor product functor is a morphism of span pairs
$\mathcal {C}$ has a (symmetric) monoidal structure such that the tensor product functor is a morphism of span pairs
i.e. given morphisms ![]() $f\colon x \to y$ and
$f\colon x \to y$ and ![]() $f' \colon x' \to y'$ in
$f' \colon x' \to y'$ in ![]() $F$, the morphism
$F$, the morphism ![]() $f \otimes f' \colon x \otimes x' \to y \otimes y'$ is also in
$f \otimes f' \colon x \otimes x' \to y \otimes y'$ is also in ![]() $F$, and given a pair of pullback squares
$F$, and given a pair of pullback squares

with ![]() $f$ and
$f$ and ![]() $f'$ in
$f'$ in ![]() $\mathcal {C}_{F}$, the commutative square
$\mathcal {C}_{F}$, the commutative square

is cartesian. Then ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ inherits a (symmetric) monoidal structure from that on
$\operatorname {SPAN}_{F}(\mathcal {C})$ inherits a (symmetric) monoidal structure from that on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Since the functor ![]() $\operatorname {SPAN}$ preserves products, it takes (commutative) algebras in span pairs to (commutative) algebras in
$\operatorname {SPAN}$ preserves products, it takes (commutative) algebras in span pairs to (commutative) algebras in ![]() $(\infty,2)$-categories.
$(\infty,2)$-categories.
Example 2.6.7 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F})$ is a span pair where
$(\mathcal {C},\mathcal {C}_{F})$ is a span pair where ![]() $\mathcal {C}$ has finite products and morphisms in
$\mathcal {C}$ has finite products and morphisms in ![]() $\mathcal {C}_{F}$ are closed under products. Products of cartesian squares are always cartesian, so in this case Corollary 2.6.6 implies that the cartesian product induces a symmetric monoidal structure on
$\mathcal {C}_{F}$ are closed under products. Products of cartesian squares are always cartesian, so in this case Corollary 2.6.6 implies that the cartesian product induces a symmetric monoidal structure on ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$. This recovers the discussion in [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 2.1] and some cases of [Reference Barwick, Glasman and ShahBGS20, Theorem 2.15].
$\operatorname {SPAN}_{F}(\mathcal {C})$. This recovers the discussion in [Reference Gaitsgory and RozenblyumGR17, Chapter 9, 2.1] and some cases of [Reference Barwick, Glasman and ShahBGS20, Theorem 2.15].
Definition 2.6.8 We say an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ is extensive if
$\mathcal {C}$ is extensive if ![]() $\mathcal {C}$ has finite coproducts and these satisfy descent in the sense that the coproduct functor
$\mathcal {C}$ has finite coproducts and these satisfy descent in the sense that the coproduct functor
 \[ \amalg \colon \prod_{i=1}^{n} \mathcal{C}_{/x_{i}} \to \mathcal{C}_{/\coprod_{i=1}^{n}x_{i}} \]
\[ \amalg \colon \prod_{i=1}^{n} \mathcal{C}_{/x_{i}} \to \mathcal{C}_{/\coprod_{i=1}^{n}x_{i}} \]
is an equivalence. (Equivalently, pullbacks of the component inclusions in finite coproducts always exist, and coproducts are disjoint and stable under pullback.)
Example 2.6.9 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is a span pair where
$(\mathcal {C}, \mathcal {C}_{F})$ is a span pair where ![]() $\mathcal {C}$ has finite coproducts and morphisms in
$\mathcal {C}$ has finite coproducts and morphisms in ![]() $\mathcal {C}_{F}$ are closed under coproducts. If
$\mathcal {C}_{F}$ are closed under coproducts. If ![]() $\mathcal {C}$ is extensive, then coproducts of cartesian squares are again cartesian. Hence, in this case the coproduct induces a symmetric monoidal structure on
$\mathcal {C}$ is extensive, then coproducts of cartesian squares are again cartesian. Hence, in this case the coproduct induces a symmetric monoidal structure on ![]() $\operatorname {SPAN}_{F}(\mathcal {C})$ by Corollary 2.6.6. The descent condition is satisfied, for instance, if
$\operatorname {SPAN}_{F}(\mathcal {C})$ by Corollary 2.6.6. The descent condition is satisfied, for instance, if ![]() $\mathcal {C}$ is an
$\mathcal {C}$ is an ![]() $\infty$-topos, or in the category of sets. See also [Reference BarwickBar17, § 4], where
$\infty$-topos, or in the category of sets. See also [Reference BarwickBar17, § 4], where ![]() $\mathcal {C}$ is called ‘disjunctive’ if
$\mathcal {C}$ is called ‘disjunctive’ if ![]() $\mathcal {C}$ is extensive and has pullbacks; in this case the coproduct in
$\mathcal {C}$ is extensive and has pullbacks; in this case the coproduct in ![]() $\mathcal {C}$ gives both the product and coproduct in
$\mathcal {C}$ gives both the product and coproduct in ![]() $\operatorname {Span}(\mathcal {C})$ by [Reference BarwickBar17, Proposition 4.3].
$\operatorname {Span}(\mathcal {C})$ by [Reference BarwickBar17, Proposition 4.3].
Specializing the preceding discussion to bispans, we obtain the following result.
Corollary 2.6.10 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ and
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ and ![]() $(\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ are bispan triples. Then the natural morphism
$(\mathcal {C}', \mathcal {C}'_{F'}, \mathcal {C}'_{L'})$ are bispan triples. Then the natural morphism
is an equivalence.
Proof. From Corollary 2.6.5 we get a product of span pairs
and, hence, using Corollary 2.6.5 again we have
as required.
Corollary 2.6.11 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple and
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple and ![]() $\mathcal {C}$ has a (symmetric) monoidal structure such that the tensor product is a morphism of bispan triples
$\mathcal {C}$ has a (symmetric) monoidal structure such that the tensor product is a morphism of bispan triples
that is:
(1) both
 $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and  $\mathcal {C}_{L}$ are closed under
$\mathcal {C}_{L}$ are closed under  $\otimes$;
$\otimes$;(2) given a pair of pullback squares
with
 $f$ and
$f$ and  $f'$ either both in
$f'$ either both in  $F$ or both in
$F$ or both in  $L$, the commutative square
is cartesian;
$L$, the commutative square
is cartesian;
(3) given morphisms
 $f \colon x \to y$,
$f \colon x \to y$,  $f' \colon x' \to y'$ in
$f' \colon x' \to y'$ in  $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and  $g \colon y \to z$,
$g \colon y \to z$,  $g' \colon y' \to z'$, the diagram
obtained as the tensor product of the distributivity diagrams for
$g' \colon y' \to z'$, the diagram
obtained as the tensor product of the distributivity diagrams for
 $(f,g)$ and
$(f,g)$ and  $(f',g')$, is a distributivity diagram for
$(f',g')$, is a distributivity diagram for  $(f \otimes f', g \otimes g')$.Footnote 8
$(f \otimes f', g \otimes g')$.Footnote 8
Then ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ inherits a (symmetric) monoidal structure from that on
${\text {BISPAN}}_{F,L}(\mathcal {C})$ inherits a (symmetric) monoidal structure from that on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Example 2.6.12 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple such that
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple such that ![]() $\mathcal {C}$ is extensive and morphisms in
$\mathcal {C}$ is extensive and morphisms in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $\mathcal {C}_{L}$ are closed under coproducts. Then the coproduct satisfies the conditions of Corollary 2.6.11: The descent condition implies that coproducts of cartesian squares are cartesian, and the condition on distributivity diagrams amounts to asking for the natural map
$\mathcal {C}_{L}$ are closed under coproducts. Then the coproduct satisfies the conditions of Corollary 2.6.11: The descent condition implies that coproducts of cartesian squares are cartesian, and the condition on distributivity diagrams amounts to asking for the natural map
to be an equivalence; this is true because by descent we have
 \begin{align*} {\text {Map}}_{/z \amalg z'}(u \amalg u', g_{*}f \amalg g'_{*}f') & \simeq {\text {Map}}_{/z}(u, g_{*}f) \times {\text {Map}}_{/z'}(u', g'_{*}f') \\ & \simeq {\text {Map}}_{/y}(g^{*}u, f) \times {\text {Map}}_{/y'}(g'^{*}u',f') \\ & \simeq {\text {Map}}_{/y \amalg y'}(g^{*}u \amalg g'^{*}u', f \amalg f') \\ & \simeq {\text {Map}}_{/y \amalg y'}((g \amalg g')^{*}(u \amalg u'), f \amalg f') \\ & \simeq {\text {Map}}_{/y \amalg y'}(u \amalg u', (g \amalg g')_{*}(f \amalg f')). \end{align*}
\begin{align*} {\text {Map}}_{/z \amalg z'}(u \amalg u', g_{*}f \amalg g'_{*}f') & \simeq {\text {Map}}_{/z}(u, g_{*}f) \times {\text {Map}}_{/z'}(u', g'_{*}f') \\ & \simeq {\text {Map}}_{/y}(g^{*}u, f) \times {\text {Map}}_{/y'}(g'^{*}u',f') \\ & \simeq {\text {Map}}_{/y \amalg y'}(g^{*}u \amalg g'^{*}u', f \amalg f') \\ & \simeq {\text {Map}}_{/y \amalg y'}((g \amalg g')^{*}(u \amalg u'), f \amalg f') \\ & \simeq {\text {Map}}_{/y \amalg y'}(u \amalg u', (g \amalg g')_{*}(f \amalg f')). \end{align*}
for an object ![]() $u \amalg u'$ over
$u \amalg u'$ over ![]() $z \amalg z'$. The coproduct therefore induces a symmetric monoidal structure on
$z \amalg z'$. The coproduct therefore induces a symmetric monoidal structure on ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$.Footnote 9
${\text {BISPAN}}_{F,L}(\mathcal {C})$.Footnote 9
Remark 2.6.13 Suppose ![]() $\mathcal {C}$ is a locally cartesian closed and extensive
$\mathcal {C}$ is a locally cartesian closed and extensive ![]() $\infty$-category. Then the symmetric monoidal structure on
$\infty$-category. Then the symmetric monoidal structure on ![]() ${\text {Bispan}}(\mathcal {C})$ induced by the coproduct in
${\text {Bispan}}(\mathcal {C})$ induced by the coproduct in ![]() $\mathcal {C}$ is a cartesian product: we have
$\mathcal {C}$ is a cartesian product: we have
 \begin{align*} {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, x \amalg y) & \simeq \{c \leftarrow a \to b \to x \amalg y \} \\ & \simeq \{c \leftarrow a_{x} \amalg a_{y} \to b_{x} \amalg b_{y} \to x \amalg y \} \\ & \simeq \{c \leftarrow a_{x} \to b_{x} \to x\} \times \{c \leftarrow a_{y} \to b_{y} \to y \} \\ & \simeq {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, x) \times {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, y). \end{align*}
\begin{align*} {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, x \amalg y) & \simeq \{c \leftarrow a \to b \to x \amalg y \} \\ & \simeq \{c \leftarrow a_{x} \amalg a_{y} \to b_{x} \amalg b_{y} \to x \amalg y \} \\ & \simeq \{c \leftarrow a_{x} \to b_{x} \to x\} \times \{c \leftarrow a_{y} \to b_{y} \to y \} \\ & \simeq {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, x) \times {\text {Map}}_{{\text {Bispan}}(\mathcal{C})}(c, y). \end{align*}
Moreover, we have the same identification for ![]() $\infty$-categories of morphisms, so this is actually an
$\infty$-categories of morphisms, so this is actually an ![]() $(\infty,2)$-categorical product. However, this is not a coproduct in bispans: in particular,
$(\infty,2)$-categorical product. However, this is not a coproduct in bispans: in particular, ![]() $\emptyset$ is not an initial object, since we have
$\emptyset$ is not an initial object, since we have
which is not, in general, contractible.
Remark 2.6.14 For any ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ we can consider the minimal bispan triple
$\mathcal {C}$ we can consider the minimal bispan triple ![]() $\mathcal {C}^{\flat } := (\mathcal {C}, \mathcal {C}^{\simeq }, \mathcal {C}^{\simeq })$ where the morphisms in
$\mathcal {C}^{\flat } := (\mathcal {C}, \mathcal {C}^{\simeq }, \mathcal {C}^{\simeq })$ where the morphisms in ![]() $\mathcal {C}_{F}$ and
$\mathcal {C}_{F}$ and ![]() $\mathcal {C}_{L}$ are just the equivalences. Any functor gives a morphism of minimal bispan triples, so we have a functor
$\mathcal {C}_{L}$ are just the equivalences. Any functor gives a morphism of minimal bispan triples, so we have a functor
that is, moreover, fully faithful. The ![]() $\infty$-category
$\infty$-category ![]() ${\text {Trip}}$ is then a
${\text {Trip}}$ is then a ![]() ${\text {Cat}}_\infty$-module via cartesian products with
${\text {Cat}}_\infty$-module via cartesian products with ![]() $(-)^{\flat }$. We also have a natural equivalence
$(-)^{\flat }$. We also have a natural equivalence ![]() ${\text {BISPAN}}(\mathcal {C}^{\flat }) \simeq \mathcal {C}$ as all functors are distributive. This means the functor
${\text {BISPAN}}(\mathcal {C}^{\flat }) \simeq \mathcal {C}$ as all functors are distributive. This means the functor ![]() ${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$ is a morphism of
${\text {BISPAN}} \colon {\text {Trip}} \to {\text {Cat}}_{(\infty,2)}$ is a morphism of ![]() ${\text {Cat}}_\infty$-modules, which we can view as a functor of
${\text {Cat}}_\infty$-modules, which we can view as a functor of ![]() $(\infty,2)$-categories using the recent results of Heine [Reference HeineHei23]. Moreover, the natural transformation
$(\infty,2)$-categories using the recent results of Heine [Reference HeineHei23]. Moreover, the natural transformation ![]() $\operatorname {Span}_{F}(\mathcal {C}) \to {\text {BISPAN}}_{F,L}(\mathcal {C})$ is a transformation of
$\operatorname {Span}_{F}(\mathcal {C}) \to {\text {BISPAN}}_{F,L}(\mathcal {C})$ is a transformation of ![]() ${\text {Cat}}_\infty$-modules, which means the universal property of
${\text {Cat}}_\infty$-modules, which means the universal property of ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C})$ is actually
${\text {BISPAN}}_{F,L}(\mathcal {C})$ is actually ![]() ${\text {Cat}}_\infty$-natural.
${\text {Cat}}_\infty$-natural.
3. Examples of distributivity
3.1 Bispans in finite sets and symmetric monoidal  $\infty$-categories
$\infty$-categories
In this subsection we consider the relationship between symmetric monoidal ![]() $\infty$-categories and bispans in finite sets. We first recall that symmetric monoidal
$\infty$-categories and bispans in finite sets. We first recall that symmetric monoidal ![]() $\infty$-categories can be described in terms of functors from spans of finite sets, and then show that the resulting functor is distributive if and only if the tensor product commutes with finite coproducts in each variable. Our universal property then gives a (product-preserving) functor from bispans in finite sets, which we can interpret as a semiring structure with the coproduct as addition and the tensor product as multiplication.
$\infty$-categories can be described in terms of functors from spans of finite sets, and then show that the resulting functor is distributive if and only if the tensor product commutes with finite coproducts in each variable. Our universal property then gives a (product-preserving) functor from bispans in finite sets, which we can interpret as a semiring structure with the coproduct as addition and the tensor product as multiplication.
Notation 3.1.1 We write ![]() $\mathbb {F}$ for the category of finite sets and
$\mathbb {F}$ for the category of finite sets and ![]() $\mathbb {F}_{*}$ for the category of finite pointed sets and base-point-preserving maps; every object of
$\mathbb {F}_{*}$ for the category of finite pointed sets and base-point-preserving maps; every object of ![]() $\mathbb {F}_{*}$ is isomorphic to one of the form
$\mathbb {F}_{*}$ is isomorphic to one of the form ![]() $\langle n \rangle := (\{0,\ldots,n\},0)$. For
$\langle n \rangle := (\{0,\ldots,n\},0)$. For ![]() $I \in \mathbb {F}$ we write
$I \in \mathbb {F}$ we write ![]() $I_{+}$ for the pointed set
$I_{+}$ for the pointed set ![]() $(I \amalg \{*\}, *)$ obtained by adding a disjoint base point to
$(I \amalg \{*\}, *)$ obtained by adding a disjoint base point to ![]() $I$.
$I$.
Definition 3.1.2 If ![]() $\mathcal {C}$ is an
$\mathcal {C}$ is an ![]() $\infty$-category with finite products, a commutative monoid in
$\infty$-category with finite products, a commutative monoid in ![]() $\mathcal {C}$ is a functor
$\mathcal {C}$ is a functor ![]() $\Phi \colon \mathbb {F}_{*} \to \mathcal {C}$ such that for every
$\Phi \colon \mathbb {F}_{*} \to \mathcal {C}$ such that for every ![]() $n=0,1,\ldots$ the map
$n=0,1,\ldots$ the map
 \[ \Phi(\langle n \rangle) \xrightarrow{(\Phi(\rho_{i}))_{i=1,\ldots,n}} \prod_{i=1}^{n} \Phi(\langle 1 \rangle) \]
\[ \Phi(\langle n \rangle) \xrightarrow{(\Phi(\rho_{i}))_{i=1,\ldots,n}} \prod_{i=1}^{n} \Phi(\langle 1 \rangle) \]
is an equivalence, where ![]() $\rho _{i} \colon \langle n \rangle \to \langle 1 \rangle$ is defined by
$\rho _{i} \colon \langle n \rangle \to \langle 1 \rangle$ is defined by
 \[ \rho_{i}(j) = \begin{cases} 1 & \text{if $i = j$,}\\ 0 & \text{otherwise}. \end{cases} \]
\[ \rho_{i}(j) = \begin{cases} 1 & \text{if $i = j$,}\\ 0 & \text{otherwise}. \end{cases} \]
We write ![]() $\operatorname {CMon}(\mathcal {C})$ for the full subcategory of
$\operatorname {CMon}(\mathcal {C})$ for the full subcategory of ![]() ${\text {Fun}}(\mathbb {F}_{*}, \mathcal {C})$ spanned by the commutative monoids.
${\text {Fun}}(\mathbb {F}_{*}, \mathcal {C})$ spanned by the commutative monoids.
Notation 3.1.3 If ![]() $\mathcal {C}, \mathcal {D}$ are
$\mathcal {C}, \mathcal {D}$ are ![]() $\infty$-categories with finite products, we write
$\infty$-categories with finite products, we write ![]() ${\text {Fun}}^{\times }(\mathcal {C},\mathcal {D})$ for the full subcategory of
${\text {Fun}}^{\times }(\mathcal {C},\mathcal {D})$ for the full subcategory of ![]() ${\text {Fun}}(\mathcal {C},\mathcal {D})$ spanned by the functors that preserve finite products.
${\text {Fun}}(\mathcal {C},\mathcal {D})$ spanned by the functors that preserve finite products.
Remark 3.1.4 The category ![]() $\mathbb {F}_{*}$ can be identified with the subcategory of
$\mathbb {F}_{*}$ can be identified with the subcategory of ![]() $\operatorname {Span}(\mathbb {F})$ whose morphisms are the spans
$\operatorname {Span}(\mathbb {F})$ whose morphisms are the spans ![]() $I \xleftarrow {f} J \xrightarrow {g} K$ where
$I \xleftarrow {f} J \xrightarrow {g} K$ where ![]() $f$ is injective, with this corresponding to the morphism
$f$ is injective, with this corresponding to the morphism ![]() $I_{+} \to K_{+}$ given by
$I_{+} \to K_{+}$ given by
 \[ i \mapsto \begin{cases} g(j), & i = f(j),\\ *, & {\text {otherwise}}; \end{cases} \]
\[ i \mapsto \begin{cases} g(j), & i = f(j),\\ *, & {\text {otherwise}}; \end{cases} \]
we write ![]() $j \colon \mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F})$ for this subcategory inclusion.
$j \colon \mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F})$ for this subcategory inclusion.
The following description of commutative monoids in terms of spans seems to have been first proved by Cranch [Reference CranchCra10, Reference CranchCra11]; other proofs, as special cases of various generalizations, can be found in [Reference GlasmanGla17, Reference HarpazHar20, Reference Bachmann and HoyoisBH21].
Proposition 3.1.5 Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $\infty$-category with finite products. Restriction along the inclusion
$\infty$-category with finite products. Restriction along the inclusion ![]() $j \colon \mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F})$ gives an equivalence
$j \colon \mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F})$ gives an equivalence
with the inverse given by right Kan extension along the functor ![]() $j$.
$j$.
Proof. In the stated form, this is [Reference Bachmann and HoyoisBH21, Proposition C.1].
Remark 3.1.6 The functor ![]() $\Phi \colon \operatorname {Span}(\mathbb {F}) \to {\text {Cat}}_\infty$ corresponding to a symmetric monoidal
$\Phi \colon \operatorname {Span}(\mathbb {F}) \to {\text {Cat}}_\infty$ corresponding to a symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ admits the following description:
$\mathcal {C}$ admits the following description:
•
 $\Phi (I) \simeq \prod _{i \in I} \mathcal {C} \simeq {\text {Fun}}(I,\mathcal {C})$;
$\Phi (I) \simeq \prod _{i \in I} \mathcal {C} \simeq {\text {Fun}}(I,\mathcal {C})$;• for
 $f \colon I \to J$, the functor
$f \colon I \to J$, the functor  $f^{\circledast } \colon {\text {Fun}}(J,\mathcal {C}) \to {\text {Fun}}(I, \mathcal {C})$ is that given by composition with
$f^{\circledast } \colon {\text {Fun}}(J,\mathcal {C}) \to {\text {Fun}}(I, \mathcal {C})$ is that given by composition with  $f$;
$f$;• for
 $f \colon I \to J$, the functor
is given by tensoring the components corresponding to the preimages of each
$f \colon I \to J$, the functor
is given by tensoring the components corresponding to the preimages of each \[ f_{\otimes} \colon {\text {Fun}}(I, \mathcal{C}) \simeq \prod_{j \in J} \prod_{i \in I_{j}} \mathcal{C} \to \prod_{j \in J} \mathcal{C} \]
\[ f_{\otimes} \colon {\text {Fun}}(I, \mathcal{C}) \simeq \prod_{j \in J} \prod_{i \in I_{j}} \mathcal{C} \to \prod_{j \in J} \mathcal{C} \]
 $j \in J$.
$j \in J$.
In particular, for ![]() $q \colon I \to *$ the functor
$q \colon I \to *$ the functor ![]() $q_{\otimes } \colon {\text {Fun}}(I, \mathcal {C}) \to \mathcal {C}$ takes
$q_{\otimes } \colon {\text {Fun}}(I, \mathcal {C}) \to \mathcal {C}$ takes ![]() $\phi \colon I \to \mathcal {C}$ to
$\phi \colon I \to \mathcal {C}$ to ![]() $\bigotimes _{i \in I} \phi (i)$, while
$\bigotimes _{i \in I} \phi (i)$, while ![]() $q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(I, \mathcal {C})$ is the diagonal functor.
$q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(I, \mathcal {C})$ is the diagonal functor.
Proposition 3.1.7 Suppose ![]() $\Phi \colon \operatorname {Span}(\mathbb {F}) \to {\text {Cat}}_\infty$ is a product-preserving functor, corresponding to a symmetric monoidal structure on
$\Phi \colon \operatorname {Span}(\mathbb {F}) \to {\text {Cat}}_\infty$ is a product-preserving functor, corresponding to a symmetric monoidal structure on ![]() $\mathcal {C} = \Phi (*)$. Then
$\mathcal {C} = \Phi (*)$. Then ![]() $\Phi$ is distributive if and only if
$\Phi$ is distributive if and only if ![]() $\mathcal {C}$ has finite coproducts and the symmetric monoidal structure is compatible with these, i.e. the tensor product preserves finite coproducts in each variable.
$\mathcal {C}$ has finite coproducts and the symmetric monoidal structure is compatible with these, i.e. the tensor product preserves finite coproducts in each variable.
Proof. For ![]() $I \in \mathbb {F}$, the functor
$I \in \mathbb {F}$, the functor ![]() $q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(I, \mathcal {C})$ corresponding to the morphism
$q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(I, \mathcal {C})$ corresponding to the morphism ![]() $q \colon I \to *$ is the diagonal. This has a left adjoint if and only if
$q \colon I \to *$ is the diagonal. This has a left adjoint if and only if ![]() $\mathcal {C}$ admits all
$\mathcal {C}$ admits all ![]() $I$-indexed colimits, i.e.
$I$-indexed colimits, i.e. ![]() $\mathcal {C}$ has
$\mathcal {C}$ has ![]() $I$-indexed coproducts. Moreover, if
$I$-indexed coproducts. Moreover, if ![]() $\mathcal {C}$ has finite coproducts, then the functor
$\mathcal {C}$ has finite coproducts, then the functor ![]() $f^{\circledast } \colon {\text {Fun}}(J, \mathcal {C}) \to {\text {Fun}}(I,\mathcal {C})$ given by composition with
$f^{\circledast } \colon {\text {Fun}}(J, \mathcal {C}) \to {\text {Fun}}(I,\mathcal {C})$ given by composition with ![]() $f \colon I \to J$ has a left adjoint for any
$f \colon I \to J$ has a left adjoint for any ![]() $f$, since all pointwise left Kan extensions along
$f$, since all pointwise left Kan extensions along ![]() $f$ exist in
$f$ exist in ![]() $\mathcal {C}$. Given a cartesian square
$\mathcal {C}$. Given a cartesian square

in ![]() $\mathbb {F}$, the mate transformation
$\mathbb {F}$, the mate transformation
is then automatically an equivalence, since for ![]() $\phi \colon J' \to \mathcal {C}$ this is given at
$\phi \colon J' \to \mathcal {C}$ this is given at ![]() $i \in I$ by the natural map
$i \in I$ by the natural map
which is an equivalence since these fibres are canonically isomorphic. This proves that ![]() $\Phi$ is left adjointable if and only if
$\Phi$ is left adjointable if and only if ![]() $\mathcal {C}$ admits finite coproducts.
$\mathcal {C}$ admits finite coproducts.
Given morphisms ![]() $l \colon I \to J$ and
$l \colon I \to J$ and ![]() $f \colon J \to K$ in
$f \colon J \to K$ in ![]() $\mathbb {F}$, we have the distributivity square
$\mathbb {F}$, we have the distributivity square

where ![]() $K'_{k} \cong \prod _{j \in J_{k}} I_{j}$. The distributivity transformation
$K'_{k} \cong \prod _{j \in J_{k}} I_{j}$. The distributivity transformation ![]() $h_{\oplus }f'_{\otimes }\epsilon ^{\circledast } \to f_{\otimes }l_{\oplus }$ is given for
$h_{\oplus }f'_{\otimes }\epsilon ^{\circledast } \to f_{\otimes }l_{\oplus }$ is given for ![]() $\phi \colon I \to \mathcal {C}$ at
$\phi \colon I \to \mathcal {C}$ at ![]() $k \in K$ by the canonical map
$k \in K$ by the canonical map
 \[ \coprod_{(i_{j})_{j} \in \prod_{j \in J_{k}} I_{j}} \bigotimes_{j \in J_{k}} \phi(i_{j}) \to \bigotimes_{j \in J_{k}} \bigg( \coprod_{i \in I_{j}} \phi(i)\bigg). \]
\[ \coprod_{(i_{j})_{j} \in \prod_{j \in J_{k}} I_{j}} \bigotimes_{j \in J_{k}} \phi(i_{j}) \to \bigotimes_{j \in J_{k}} \bigg( \coprod_{i \in I_{j}} \phi(i)\bigg). \]
This is an equivalence if ![]() $\otimes$ preserves finite coproducts in each variable. Conversely, for
$\otimes$ preserves finite coproducts in each variable. Conversely, for ![]() $K \in \mathbb {F}$ we have, in particular, the distributivity diagram
$K \in \mathbb {F}$ we have, in particular, the distributivity diagram

where ![]() $q$ is the unique map
$q$ is the unique map ![]() $K \to *$ and
$K \to *$ and ![]() $\nabla$ are fold maps. The corresponding distributivity transformation is given for
$\nabla$ are fold maps. The corresponding distributivity transformation is given for ![]() $\alpha \colon K \amalg * \to \mathcal {C}$ by
$\alpha \colon K \amalg * \to \mathcal {C}$ by
 \[ \coprod_{k \in K} \big( \alpha(k) \otimes \alpha(*)\big) \to \bigg(\coprod_{k \in K} \alpha(k) \bigg) \otimes \alpha(*). \]
\[ \coprod_{k \in K} \big( \alpha(k) \otimes \alpha(*)\big) \to \bigg(\coprod_{k \in K} \alpha(k) \bigg) \otimes \alpha(*). \]
If ![]() $\Phi$ is distributive, then this is an equivalence for all
$\Phi$ is distributive, then this is an equivalence for all ![]() $K$ and
$K$ and ![]() $\alpha$, which is precisely the condition that
$\alpha$, which is precisely the condition that ![]() $\otimes$ preserves finite coproducts in each variable.
$\otimes$ preserves finite coproducts in each variable.
Corollary 3.1.8 Product-preserving functors ![]() ${\text {BISPAN}}(\mathbb {F}) \to {\text {CAT}}_{\infty }$ correspond to symmetric monoidal
${\text {BISPAN}}(\mathbb {F}) \to {\text {CAT}}_{\infty }$ correspond to symmetric monoidal ![]() $\infty$-categories that are compatible with finite coproducts.
$\infty$-categories that are compatible with finite coproducts.
Proof. By Theorem 2.5.1, functors ![]() ${\text {BISPAN}}(\mathbb {F}) \to {\text {CAT}}_{\infty }$ correspond to distributive functors
${\text {BISPAN}}(\mathbb {F}) \to {\text {CAT}}_{\infty }$ correspond to distributive functors ![]() $\operatorname {Span}(\mathbb {F}) \to {\text {CAT}}_{\infty }$. Moreover, from Remark 2.6.13 we know that the product in
$\operatorname {Span}(\mathbb {F}) \to {\text {CAT}}_{\infty }$. Moreover, from Remark 2.6.13 we know that the product in ![]() ${\text {BISPAN}}(\mathbb {F})$ is given by the coproduct in
${\text {BISPAN}}(\mathbb {F})$ is given by the coproduct in ![]() $\mathbb {F}$, just as in
$\mathbb {F}$, just as in ![]() $\operatorname {Span}(\mathbb {F})$, so product-preserving functors from
$\operatorname {Span}(\mathbb {F})$, so product-preserving functors from ![]() ${\text {BISPAN}}(\mathbb {F})$ correspond to product-preserving distributive functors under this equivalence. By Propositions 3.1.7 and 3.1.5, the latter are equivalent to symmetric monoidal
${\text {BISPAN}}(\mathbb {F})$ correspond to product-preserving distributive functors under this equivalence. By Propositions 3.1.7 and 3.1.5, the latter are equivalent to symmetric monoidal ![]() $\infty$-categories that are compatible with finite coproducts.
$\infty$-categories that are compatible with finite coproducts.
3.2 Bispans in spaces and symmetric monoidal  $\infty$-categories
$\infty$-categories
In this section we consider a variant of the results of the preceding one: symmetric monoidal ![]() $\infty$-categories can also be described in terms of spans of spaces, and we will prove that the resulting functor is distributive (with respect to all morphisms of spaces) if and only if the tensor product commutes with colimits indexed by
$\infty$-categories can also be described in terms of spans of spaces, and we will prove that the resulting functor is distributive (with respect to all morphisms of spaces) if and only if the tensor product commutes with colimits indexed by ![]() $\infty$-groupoids. This applies in many examples, since most naturally occurring tensor products are compatible with all colimits.
$\infty$-groupoids. This applies in many examples, since most naturally occurring tensor products are compatible with all colimits.
Notation 3.2.1 We write ![]() $\mathcal {S}_{\mathrm {fin}}$ for the subcategory of
$\mathcal {S}_{\mathrm {fin}}$ for the subcategory of ![]() $\mathcal {S}$ containing only the morphisms whose fibres are equivalent to finite sets. Then
$\mathcal {S}$ containing only the morphisms whose fibres are equivalent to finite sets. Then ![]() $(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$ is a span pair.
$(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$ is a span pair.
Remark 3.2.2 If ![]() $f \colon X \to I$ is a morphism in
$f \colon X \to I$ is a morphism in ![]() $\mathcal {S}_{\mathrm {fin}}$ and
$\mathcal {S}_{\mathrm {fin}}$ and ![]() $I$ is a finite set, then the straightening equivalence
$I$ is a finite set, then the straightening equivalence
implies that ![]() $X$ is an
$X$ is an ![]() $I$-indexed coproduct of finite sets, and so is itself a finite set. It follows that the functor
$I$-indexed coproduct of finite sets, and so is itself a finite set. It follows that the functor ![]() $\operatorname {Span}(\mathbb {F}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ induced by the morphism of span pairs
$\operatorname {Span}(\mathbb {F}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ induced by the morphism of span pairs ![]() $(\mathbb {F},\mathbb {F}) \to (\mathcal {S},\mathcal {S}_{\mathrm {fin}})$ is fully faithful.
$(\mathbb {F},\mathbb {F}) \to (\mathcal {S},\mathcal {S}_{\mathrm {fin}})$ is fully faithful.
Proposition 3.2.3 Let ![]() $\mathcal {C}$ be a complete
$\mathcal {C}$ be a complete ![]() $\infty$-category. Right Kan extension along the fully faithful functor
$\infty$-category. Right Kan extension along the fully faithful functor ![]() $\operatorname {Span}(\mathbb {F}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ identifies
$\operatorname {Span}(\mathbb {F}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ identifies ![]() ${\text {Fun}}^{\times }(\operatorname {Span}(\mathbb {F}), \mathcal {C})$ with the full subcategory
${\text {Fun}}^{\times }(\operatorname {Span}(\mathbb {F}), \mathcal {C})$ with the full subcategory ![]() ${\text {Fun}}^{{\text {RKE}}}(\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}), \mathcal {C})$ of
${\text {Fun}}^{{\text {RKE}}}(\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}), \mathcal {C})$ of ![]() ${\text {Fun}}(\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}), \mathcal {C})$ spanned by functors
${\text {Fun}}(\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}), \mathcal {C})$ spanned by functors ![]() $\Phi$ such that
$\Phi$ such that ![]() $\Phi |_{\mathcal {S}^{{\text {op}}}}$ is right Kan extended from
$\Phi |_{\mathcal {S}^{{\text {op}}}}$ is right Kan extended from ![]() $\{*\}$.
$\{*\}$.
Proof. This is a special case of [Reference Bachmann and HoyoisBH21, Proposition C.18].
Combining this with Proposition 3.1.5, we have the following.
Corollary 3.2.4 Let ![]() $\mathcal {C}$ be a complete
$\mathcal {C}$ be a complete ![]() $\infty$-category. There is an equivalence
$\infty$-category. There is an equivalence
given by right Kan extension along ![]() $\mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F}) \hookrightarrow \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$.
$\mathbb {F}_{*} \to \operatorname {Span}(\mathbb {F}) \hookrightarrow \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$.
Remark 3.2.5 In particular, symmetric monoidal ![]() $\infty$-categories can be identified with functors
$\infty$-categories can be identified with functors ![]() $\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ whose restrictions to
$\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ whose restrictions to ![]() $\mathcal {S}^{{\text {op}}}$ preserve limits. If
$\mathcal {S}^{{\text {op}}}$ preserve limits. If ![]() $\mathcal {C}$ is a symmetric monoidal
$\mathcal {C}$ is a symmetric monoidal ![]() $\infty$-category, the corresponding functor
$\infty$-category, the corresponding functor ![]() $\Phi \colon \operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ admits the following description (analogous to Remark 3.1.6):
$\Phi \colon \operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ admits the following description (analogous to Remark 3.1.6):
• for
 $X \in \mathcal {S}$,
$X \in \mathcal {S}$,  $\Phi (X) \simeq \lim _{x \in X} \Phi (\{x\}) \simeq {\text {Fun}}(X, \mathcal {C})$;
$\Phi (X) \simeq \lim _{x \in X} \Phi (\{x\}) \simeq {\text {Fun}}(X, \mathcal {C})$;• for
 $f \colon X \to Y$ in
$f \colon X \to Y$ in  $\mathcal {S}$, the functor
$\mathcal {S}$, the functor  $f^{\circledast } \colon {\text {Fun}}(Y, \mathcal {C}) \to {\text {Fun}}(X, \mathcal {C})$ is given by composition with
$f^{\circledast } \colon {\text {Fun}}(Y, \mathcal {C}) \to {\text {Fun}}(X, \mathcal {C})$ is given by composition with  $f$;
$f$;• for
 $g \colon E \to B$ in
$g \colon E \to B$ in  $\mathcal {S}_{\mathrm {fin}}$, the functor
$\mathcal {S}_{\mathrm {fin}}$, the functor  $g_{\otimes } \colon {\text {Fun}}(E, \mathcal {C}) \to {\text {Fun}}(B,\mathcal {C})$ is given by tensoring fibrewise along
$g_{\otimes } \colon {\text {Fun}}(E, \mathcal {C}) \to {\text {Fun}}(B,\mathcal {C})$ is given by tensoring fibrewise along  $g$, i.e. for
$g$, i.e. for  $\phi \colon E \to B$ we have
$\phi \colon E \to B$ we have
 \[ (g_{\otimes} \phi)(b) \simeq \bigotimes_{e \in E_{b}} \phi(e). \]
\[ (g_{\otimes} \phi)(b) \simeq \bigotimes_{e \in E_{b}} \phi(e). \]
In particular, for ![]() $q \colon X \to *$ the functor
$q \colon X \to *$ the functor ![]() $q^{\circledast }$ is the diagonal functor, while if
$q^{\circledast }$ is the diagonal functor, while if ![]() $X$ is a finite set, the functor
$X$ is a finite set, the functor ![]() $q_{\otimes }$ is the
$q_{\otimes }$ is the ![]() $X$-indexed tensor product.
$X$-indexed tensor product.
We will identify when such functors from ![]() $\operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ are distributive with respect to bispan triples of the following form.
$\operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$ are distributive with respect to bispan triples of the following form.
Lemma 3.2.6 Let ![]() $\mathcal {K}$ be a full subcategory of
$\mathcal {K}$ be a full subcategory of ![]() $\mathcal {S}$ with the following properties:
$\mathcal {S}$ with the following properties:
• if
 $p \colon E \to B$ is a morphism in
$p \colon E \to B$ is a morphism in  $\mathcal {S}$ such that
$\mathcal {S}$ such that  $B \in \mathcal {K}$ and
$B \in \mathcal {K}$ and  $E_{b} \in \mathcal {K}$ for all
$E_{b} \in \mathcal {K}$ for all  $b \in B$, then
$b \in B$, then  $E \in \mathcal {K}$;
$E \in \mathcal {K}$;•
 $\mathcal {K}$ is closed under finite products.
$\mathcal {K}$ is closed under finite products.
This implies that morphisms in ![]() $\mathcal {S}$ whose fibres lie in
$\mathcal {S}$ whose fibres lie in ![]() $\mathcal {K}$ are closed under composition, giving a subcategory
$\mathcal {K}$ are closed under composition, giving a subcategory ![]() $\mathcal {S}_{\mathcal {K}}$ of
$\mathcal {S}_{\mathcal {K}}$ of ![]() $\mathcal {S}$. Then
$\mathcal {S}$. Then ![]() $(\mathcal {S}, \mathcal {S}_{\mathrm {fin}}, \mathcal {S}_{\mathcal {K}})$ is a bispan triple.
$(\mathcal {S}, \mathcal {S}_{\mathrm {fin}}, \mathcal {S}_{\mathcal {K}})$ is a bispan triple.
Proof. Suppose ![]() $f \colon X \to Y$ and
$f \colon X \to Y$ and ![]() $g \colon Y \to Z$ are morphisms whose fibres lie in
$g \colon Y \to Z$ are morphisms whose fibres lie in ![]() $\mathcal {K}$. We have a morphism
$\mathcal {K}$. We have a morphism ![]() $X_{z} \to Y_{z}$ between the fibres of
$X_{z} \to Y_{z}$ between the fibres of ![]() $gf$ and
$gf$ and ![]() $g$ at
$g$ at ![]() $z \in Z$, whose fibre at
$z \in Z$, whose fibre at ![]() $y \in Y_{z}$ is equivalent to
$y \in Y_{z}$ is equivalent to ![]() $X_{y}$. Since
$X_{y}$. Since ![]() $Y_{z}$ and
$Y_{z}$ and ![]() $X_{y}$ lie in
$X_{y}$ lie in ![]() $\mathcal {K}$ for all
$\mathcal {K}$ for all ![]() $z \in Z, y \in Y$, it follows that
$z \in Z, y \in Y$, it follows that ![]() $X_{z}$ also lies in
$X_{z}$ also lies in ![]() $\mathcal {K}$. Thus, we do indeed have a subcategory
$\mathcal {K}$. Thus, we do indeed have a subcategory ![]() $\mathcal {S}_{\mathcal {K}}$ of morphisms whose fibres lie in
$\mathcal {S}_{\mathcal {K}}$ of morphisms whose fibres lie in ![]() $\mathcal {K}$. Such morphisms are obviously preserved under base change, and so
$\mathcal {K}$. Such morphisms are obviously preserved under base change, and so ![]() $(\mathcal {S},\mathcal {S}_{\mathcal {K}})$ is a span pair.
$(\mathcal {S},\mathcal {S}_{\mathcal {K}})$ is a span pair.
All distributivity diagrams exist in ![]() $\mathcal {S}$ since this is a locally cartesian closed
$\mathcal {S}$ since this is a locally cartesian closed ![]() $\infty$-category; see Remark 2.4.7. To show that
$\infty$-category; see Remark 2.4.7. To show that ![]() $(\mathcal {S}, \mathcal {S}_{\mathrm {fin}}, \mathcal {S}_{\mathcal {K}})$ is a bispan triple it therefore only remains to check that if
$(\mathcal {S}, \mathcal {S}_{\mathrm {fin}}, \mathcal {S}_{\mathcal {K}})$ is a bispan triple it therefore only remains to check that if ![]() $l \colon X \to Y$ is a morphism in
$l \colon X \to Y$ is a morphism in ![]() $\mathcal {S}_{\mathcal {K}}$ and
$\mathcal {S}_{\mathcal {K}}$ and ![]() $f \colon Y \to Z$ is a morphism in
$f \colon Y \to Z$ is a morphism in ![]() $\mathcal {S}_{\mathrm {fin}}$, then
$\mathcal {S}_{\mathrm {fin}}$, then ![]() $f_{*}l$ is also a morphism in
$f_{*}l$ is also a morphism in ![]() $\mathcal {S}_{\mathcal {K}}$. But we have
$\mathcal {S}_{\mathcal {K}}$. But we have
which is a finite product of objects of ![]() $\mathcal {K}$, and so again lies in
$\mathcal {K}$, and so again lies in ![]() $\mathcal {K}$ by assumption.
$\mathcal {K}$ by assumption.
Examples 3.2.7 We can take ![]() $\mathcal {K}$ in Lemma 3.2.6 to consist of:
$\mathcal {K}$ in Lemma 3.2.6 to consist of:
• finite sets;
• all spaces;
•
 $\pi$-finite spaces,Footnote 10 as follows by examining the long exact sequence in homotopy groups associated to a fibre sequence;
$\pi$-finite spaces,Footnote 10 as follows by examining the long exact sequence in homotopy groups associated to a fibre sequence;•
 $\kappa$-compact spacesFootnote 11 for any regular cardinal
$\kappa$-compact spacesFootnote 11 for any regular cardinal  $\kappa$, since
$\kappa$, since  $\kappa$-filtered colimits in
$\kappa$-filtered colimits in  $\mathcal {S}$ commute with
$\mathcal {S}$ commute with  $\kappa$-small limits, and the
$\kappa$-small limits, and the  $\kappa$-compact spaces are precisely the (retracts of)
$\kappa$-compact spaces are precisely the (retracts of)  $\kappa$-small
$\kappa$-small  $\infty$-groupoids.
$\infty$-groupoids.
Proposition 3.2.8 Suppose ![]() $\Phi \colon \operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ corresponds to a symmetric monoidal structure on
$\Phi \colon \operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ corresponds to a symmetric monoidal structure on ![]() $\mathcal {C} = \Phi (*)$, and let
$\mathcal {C} = \Phi (*)$, and let ![]() $\mathcal {K}$ be as in Lemma 3.2.6. Then
$\mathcal {K}$ be as in Lemma 3.2.6. Then ![]() $\Phi$ is
$\Phi$ is ![]() $\mathcal {K}$-distributive if and only if
$\mathcal {K}$-distributive if and only if ![]() $\mathcal {C}$ has
$\mathcal {C}$ has ![]() $\mathcal {K}$-indexed colimits (meaning
$\mathcal {K}$-indexed colimits (meaning ![]() $K$-indexed colimits for all
$K$-indexed colimits for all ![]() $K \in \mathcal {K}$), and the tensor product on
$K \in \mathcal {K}$), and the tensor product on ![]() $\mathcal {C}$ is compatible with such colimits (i.e. preserves them in each variable).
$\mathcal {C}$ is compatible with such colimits (i.e. preserves them in each variable).
Proof. For ![]() $K \in \mathcal {K}$, the functor
$K \in \mathcal {K}$, the functor ![]() $q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(K, \mathcal {C})$ corresponding to the morphism
$q^{\circledast } \colon \mathcal {C} \to {\text {Fun}}(K, \mathcal {C})$ corresponding to the morphism ![]() $q \colon K \to *$ is the diagonal. This has a left adjoint if and only if
$q \colon K \to *$ is the diagonal. This has a left adjoint if and only if ![]() $\mathcal {C}$ admits all
$\mathcal {C}$ admits all ![]() $K$-indexed colimits. Moreover, if
$K$-indexed colimits. Moreover, if ![]() $\mathcal {C}$ has
$\mathcal {C}$ has ![]() $\mathcal {K}$-indexed colimits, then the functor
$\mathcal {K}$-indexed colimits, then the functor ![]() $f^{\circledast } \colon {\text {Fun}}(Y, \mathcal {C}) \to {\text {Fun}}(X,\mathcal {C})$ given by composition with
$f^{\circledast } \colon {\text {Fun}}(Y, \mathcal {C}) \to {\text {Fun}}(X,\mathcal {C})$ given by composition with ![]() $f \colon X \to Y$ has a left adjoint for any
$f \colon X \to Y$ has a left adjoint for any ![]() $f$ in
$f$ in ![]() $\mathcal {S}_{\mathcal {K}}$, since all pointwise left Kan extensions along
$\mathcal {S}_{\mathcal {K}}$, since all pointwise left Kan extensions along ![]() $f$ then exist in
$f$ then exist in ![]() $\mathcal {C}$. Given a cartesian square
$\mathcal {C}$. Given a cartesian square

in ![]() $\mathcal {S}$ with
$\mathcal {S}$ with ![]() $g$ in
$g$ in ![]() $\mathcal {S}_{\mathcal {K}}$, the mate transformation
$\mathcal {S}_{\mathcal {K}}$, the mate transformation
is then automatically an equivalence, since for ![]() $\phi \colon Y' \to \mathcal {C}$ this is given at
$\phi \colon Y' \to \mathcal {C}$ this is given at ![]() $x \in X$ by the natural map
$x \in X$ by the natural map
which is an equivalence since these fibres are canonically equivalent. This proves that ![]() $\Phi$ is left adjointable if and only if
$\Phi$ is left adjointable if and only if ![]() $\mathcal {C}$ admits
$\mathcal {C}$ admits ![]() $\mathcal {K}$-indexed colimits.
$\mathcal {K}$-indexed colimits.
Given morphisms ![]() $l \colon X \to Y$ in
$l \colon X \to Y$ in ![]() $\mathcal {S}_{\mathcal {K}}$ and
$\mathcal {S}_{\mathcal {K}}$ and ![]() $f \colon Y \to Z$ in
$f \colon Y \to Z$ in ![]() $\mathcal {S}_{\mathrm {fin}}$, we have the distributivity diagram
$\mathcal {S}_{\mathrm {fin}}$, we have the distributivity diagram

where ![]() $Z'_{z} \simeq \prod _{y \in Y_{z}} X_{y}$. The distributivity transformation
$Z'_{z} \simeq \prod _{y \in Y_{z}} X_{y}$. The distributivity transformation ![]() $h_{\oplus }f'_{\otimes }\epsilon ^{\circledast } \to f_{\otimes }l_{\oplus }$ is given for
$h_{\oplus }f'_{\otimes }\epsilon ^{\circledast } \to f_{\otimes }l_{\oplus }$ is given for ![]() $\phi \colon X \to \mathcal {C}$ at
$\phi \colon X \to \mathcal {C}$ at ![]() $z \in Z$ by the canonical map
$z \in Z$ by the canonical map
This is an equivalence if ![]() $\otimes$ preserves
$\otimes$ preserves ![]() $\mathcal {K}$-indexed colimits in each variable. Conversely, for
$\mathcal {K}$-indexed colimits in each variable. Conversely, for ![]() $K \in \mathcal {K}$ we have, in particular, the distributivity diagram
$K \in \mathcal {K}$ we have, in particular, the distributivity diagram

where ![]() $q$ is the unique map
$q$ is the unique map ![]() $K \to *$ and
$K \to *$ and ![]() $\nabla$ are fold maps. The corresponding distributivity transformation is given for
$\nabla$ are fold maps. The corresponding distributivity transformation is given for ![]() $\phi \colon K \amalg * \to \mathcal {C}$ by
$\phi \colon K \amalg * \to \mathcal {C}$ by
If ![]() $\Phi$ is distributive, then this is an equivalence for all
$\Phi$ is distributive, then this is an equivalence for all ![]() $K \in \mathcal {K}$ and
$K \in \mathcal {K}$ and ![]() $\phi$, which is precisely the condition that
$\phi$, which is precisely the condition that ![]() $\otimes$ preserves
$\otimes$ preserves ![]() $\mathcal {K}$-indexed colimits in each variable.
$\mathcal {K}$-indexed colimits in each variable.
Corollary 3.2.9 Let ![]() $\mathcal {K}$ be as in Lemma 3.2.6. Then functors
$\mathcal {K}$ be as in Lemma 3.2.6. Then functors ![]() $\Phi \colon {\text {BISPAN}}_{\mathrm {fin},\mathcal {K}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ such that the restriction to
$\Phi \colon {\text {BISPAN}}_{\mathrm {fin},\mathcal {K}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ such that the restriction to ![]() $\mathcal {S}^{{\text {op}}}$ preserves limits correspond to symmetric monoidal
$\mathcal {S}^{{\text {op}}}$ preserves limits correspond to symmetric monoidal ![]() $\infty$-categories that are compatible with
$\infty$-categories that are compatible with ![]() $\mathcal {K}$-indexed colimits.
$\mathcal {K}$-indexed colimits.
Proof. By Theorem 2.5.1, functors ![]() ${\text {BISPAN}}_{\mathrm {fin},\mathcal {K}} \to {\text {CAT}}_{\infty }$ correspond to
${\text {BISPAN}}_{\mathrm {fin},\mathcal {K}} \to {\text {CAT}}_{\infty }$ correspond to ![]() $\mathcal {K}$-distributive functors
$\mathcal {K}$-distributive functors ![]() $\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$. On the other hand, we know from Corollary 3.2.4 that such functors whose restriction to
$\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$. On the other hand, we know from Corollary 3.2.4 that such functors whose restriction to ![]() $\mathcal {S}^{{\text {op}}}$ is right Kan extended from
$\mathcal {S}^{{\text {op}}}$ is right Kan extended from ![]() $\{*\}$ correspond to symmetric monoidal
$\{*\}$ correspond to symmetric monoidal ![]() $\infty$-categories, and in this case the functor is
$\infty$-categories, and in this case the functor is ![]() $\mathcal {K}$-distributive if and only if the tensor product is compatible with
$\mathcal {K}$-distributive if and only if the tensor product is compatible with ![]() $\mathcal {K}$-indexed colimits by Proposition 3.2.8.
$\mathcal {K}$-indexed colimits by Proposition 3.2.8.
3.3 Bispans in spaces and analytic monads
Our goal in this section is to relate bispans in the ![]() $\infty$-category of spaces to the polynomial and analytic functors studied in [Reference Gepner, Haugseng and KockGHK22], where it is shown that analytic monads are equivalent to
$\infty$-category of spaces to the polynomial and analytic functors studied in [Reference Gepner, Haugseng and KockGHK22], where it is shown that analytic monads are equivalent to ![]() $\infty$-operads. Using the results of the previous section we will see that there is a canonical action of every analytic monad on any symmetric monoidal
$\infty$-operads. Using the results of the previous section we will see that there is a canonical action of every analytic monad on any symmetric monoidal ![]() $\infty$-category compatible with
$\infty$-category compatible with ![]() $\infty$-groupoid-indexed colimits.
$\infty$-groupoid-indexed colimits.
We first give a general construction of a functor from bispans to ![]() $\infty$-categories using slice
$\infty$-categories using slice ![]() $\infty$-categories.
$\infty$-categories.
Proposition 3.3.1 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple. Then there is a functor of
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple. Then there is a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories ![]() ${\text {Sl}} \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$ such that:
${\text {Sl}} \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$ such that:
•
 ${\text {Sl}}(c) \simeq \mathcal {C}_{/c}^{L}$, the full subcategory of
${\text {Sl}}(c) \simeq \mathcal {C}_{/c}^{L}$, the full subcategory of  $\mathcal {C}_{/c}$ spanned by the morphisms to
$\mathcal {C}_{/c}$ spanned by the morphisms to  $c$ that lie in
$c$ that lie in  $\mathcal {C}_{L}$;
$\mathcal {C}_{L}$;• for
 $f \colon c \to c'$ in
$f \colon c \to c'$ in  $\mathcal {C}$, the functor
$\mathcal {C}$, the functor  $f^{\circledast }$ is the functor
$f^{\circledast }$ is the functor  $f^{*} \colon \mathcal {C}_{/c'}^{L} \to \mathcal {C}_{/c}^{L}$ given by pullback along
$f^{*} \colon \mathcal {C}_{/c'}^{L} \to \mathcal {C}_{/c}^{L}$ given by pullback along  $f$;
$f$;• for
 $f \colon c \to c'$ in
$f \colon c \to c'$ in  $\mathcal {C}_{L}$, the functor
$\mathcal {C}_{L}$, the functor  $f_{\oplus }$ is the functor
$f_{\oplus }$ is the functor  $f_{!} \colon \mathcal {C}_{/c}^{L} \to \mathcal {C}_{/c'}^{L}$ given by composition with
$f_{!} \colon \mathcal {C}_{/c}^{L} \to \mathcal {C}_{/c'}^{L}$ given by composition with  $f$;
$f$;• for
 $f \colon c \to c'$ in
$f \colon c \to c'$ in  $\mathcal {C}_{F}$, the functor
$\mathcal {C}_{F}$, the functor  $f_{\otimes }$ is the functor
$f_{\otimes }$ is the functor  $f_{*}\colon \mathcal {C}_{/c}^{L} \to \mathcal {C}_{/c'}^{L}$ given by the partial right adjoint to
$f_{*}\colon \mathcal {C}_{/c}^{L} \to \mathcal {C}_{/c'}^{L}$ given by the partial right adjoint to  $f^{*} \colon \mathcal {C}_{/c'} \to \mathcal {C}_{/c}$.
$f^{*} \colon \mathcal {C}_{/c'} \to \mathcal {C}_{/c}$.
Proof. Let ![]() $\mathcal {X}$ be the full subcategory of
$\mathcal {X}$ be the full subcategory of ![]() $\mathcal {C}^{\Delta ^{1}}$ spanned by the morphisms in
$\mathcal {C}^{\Delta ^{1}}$ spanned by the morphisms in ![]() $\mathcal {C}_{L}$. Then the restriction of
$\mathcal {C}_{L}$. Then the restriction of ![]() ${\text {ev}}_{1} \colon \mathcal {C}^{\Delta ^{1}} \to \mathcal {C}$ to a functor
${\text {ev}}_{1} \colon \mathcal {C}^{\Delta ^{1}} \to \mathcal {C}$ to a functor ![]() $\mathcal {X} \to \mathcal {C}$ is a cartesian fibration, with cocartesian morphisms over morphisms in
$\mathcal {X} \to \mathcal {C}$ is a cartesian fibration, with cocartesian morphisms over morphisms in ![]() $\mathcal {C}_{L} \subseteq \mathcal {C}$. This corresponds to a functor
$\mathcal {C}_{L} \subseteq \mathcal {C}$. This corresponds to a functor ![]() $\lambda \colon \mathcal {C}^{{\text {op}}} \to {\text {Cat}}_\infty$, which takes
$\lambda \colon \mathcal {C}^{{\text {op}}} \to {\text {Cat}}_\infty$, which takes ![]() $c \in \mathcal {C}$ to the
$c \in \mathcal {C}$ to the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}^{L}_{/c}$ and
$\mathcal {C}^{L}_{/c}$ and ![]() $f \colon x \to y$ to the functor
$f \colon x \to y$ to the functor ![]() $f^{*} \colon \mathcal {C}^{L}_{/y} \to \mathcal {C}^{L}_{/x}$ given by pullback along
$f^{*} \colon \mathcal {C}^{L}_{/y} \to \mathcal {C}^{L}_{/x}$ given by pullback along ![]() $f$. The functor
$f$. The functor ![]() $\lambda$ is right
$\lambda$ is right ![]() $F$-adjointable: since
$F$-adjointable: since ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple, the functor
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ is a bispan triple, the functor ![]() $f^{*}$ for
$f^{*}$ for ![]() $f \colon x \to y$ in
$f \colon x \to y$ in ![]() $\mathcal {C}_{F}$ has a right adjoint
$\mathcal {C}_{F}$ has a right adjoint ![]() $f_{*} \colon \mathcal {C}^{L}_{/x}\to \mathcal {C}^{L}_{/y}$ by Remark 2.4.5, and given a cartesian square
$f_{*} \colon \mathcal {C}^{L}_{/x}\to \mathcal {C}^{L}_{/y}$ by Remark 2.4.5, and given a cartesian square

with ![]() $f$ and
$f$ and ![]() $f'$ in
$f'$ in ![]() $\mathcal {C}_{F}$, the mate transformation
$\mathcal {C}_{F}$, the mate transformation
is an equivalence by Lemma 2.4.6. The functor ![]() $\lambda$ therefore extends canonically to a functor
$\lambda$ therefore extends canonically to a functor
by Theorem 2.2.7. We claim the underlying functor of ![]() $\infty$-categories
$\infty$-categories ![]() $\lambda '\colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ is
$\lambda '\colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ is ![]() $L$-distributive. Certainly if
$L$-distributive. Certainly if ![]() $l \colon x \to y$ is a morphism in
$l \colon x \to y$ is a morphism in ![]() $\mathcal {C}_{L}$, then the pullback functor
$\mathcal {C}_{L}$, then the pullback functor ![]() $l^{*} \colon \mathcal {C}^{L}_{/y}\to \mathcal {C}^{L}_{/x}$ has a left adjoint
$l^{*} \colon \mathcal {C}^{L}_{/y}\to \mathcal {C}^{L}_{/x}$ has a left adjoint ![]() $l_{!}$ given by composition with
$l_{!}$ given by composition with ![]() $l$; to see that the restriction of
$l$; to see that the restriction of ![]() $\lambda '$ to
$\lambda '$ to ![]() $\mathcal {C}^{{\text {op}}}$ is left
$\mathcal {C}^{{\text {op}}}$ is left ![]() $L$-adjointable it remains to observe that for any cartesian square
$L$-adjointable it remains to observe that for any cartesian square

with ![]() $l$ and
$l$ and ![]() $l'$ in
$l'$ in ![]() $\mathcal {C}_{L}$, the natural transformation
$\mathcal {C}_{L}$, the natural transformation ![]() $l'_{!}\xi ^{*} \to \eta ^{*}l_{!}$ is an equivalence, since for
$l'_{!}\xi ^{*} \to \eta ^{*}l_{!}$ is an equivalence, since for ![]() $g \colon z \to x$ in
$g \colon z \to x$ in ![]() $\mathcal {C}^{L}_{/x}$ in the diagram
$\mathcal {C}^{L}_{/x}$ in the diagram

the left square is cartesian if and only if the composite square is cartesian. To see that ![]() $\lambda '$ is also
$\lambda '$ is also ![]() $L$-distributive, consider
$L$-distributive, consider ![]() $l \colon x \to y$ in
$l \colon x \to y$ in ![]() $\mathcal {C}_{L}$ and
$\mathcal {C}_{L}$ and ![]() $f \colon y \to z$ in
$f \colon y \to z$ in ![]() $\mathcal {C}_{F}$ and form a distributivity diagram (20). The distributivity transformation
$\mathcal {C}_{F}$ and form a distributivity diagram (20). The distributivity transformation
evaluated at ![]() $l' \colon c \to x$ is a canonical map
$l' \colon c \to x$ is a canonical map
this is an equivalence by Lemma 2.5.19. It follows by Theorem 2.5.1 that ![]() $\lambda '$ extends uniquely to a functor
$\lambda '$ extends uniquely to a functor ![]() ${\text {Sl}} \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$, which, by construction, has the required properties.
${\text {Sl}} \colon {\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$, which, by construction, has the required properties.
Applying this to the bispan triple ![]() $(\mathcal {S},\mathcal {S},\mathcal {S})$ we get, in particular, the following result.
$(\mathcal {S},\mathcal {S},\mathcal {S})$ we get, in particular, the following result.
Corollary 3.3.2 There is a functor ![]() ${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ taking
${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ taking ![]() $X \in \mathcal {S}$ to
$X \in \mathcal {S}$ to ![]() $\mathcal {S}_{/X}$ and a bispan
$\mathcal {S}_{/X}$ and a bispan
to the functor ![]() $t_{!}p_{*}s^{*} \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$, where
$t_{!}p_{*}s^{*} \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$, where ![]() $s^{*}$ is given by pullback along
$s^{*}$ is given by pullback along ![]() $s$,
$s$, ![]() $p_{*}$ is the right adjoint to
$p_{*}$ is the right adjoint to ![]() $p^{*}$, and
$p^{*}$, and ![]() $t_{!}$ is given by composition with
$t_{!}$ is given by composition with ![]() $t$.
$t$.
Definition 3.3.3 A polynomial functor ![]() $F \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$ is an accessible functor that preserves weakly contractible limits. By [Reference Gepner, Haugseng and KockGHK22, Theorem 2.2.3] the polynomial functors are equivalently those functors obtained as composites
$F \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$ is an accessible functor that preserves weakly contractible limits. By [Reference Gepner, Haugseng and KockGHK22, Theorem 2.2.3] the polynomial functors are equivalently those functors obtained as composites ![]() $t_{!}p_{*}s^{*}$ for some bispan of spaces
$t_{!}p_{*}s^{*}$ for some bispan of spaces
Let ![]() $\operatorname {PolyFun}(\mathcal {S})$ be the sub-
$\operatorname {PolyFun}(\mathcal {S})$ be the sub-![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() ${\text {CAT}}_{\infty }$ whose objects are the slices
${\text {CAT}}_{\infty }$ whose objects are the slices ![]() $\mathcal {S}_{/X}$ for
$\mathcal {S}_{/X}$ for ![]() $X \in \mathcal {S}$, whose 1-morphisms are the polynomial functors, and whose 2-morphisms are the cartesian natural transformations.
$X \in \mathcal {S}$, whose 1-morphisms are the polynomial functors, and whose 2-morphisms are the cartesian natural transformations.
Remark 3.3.4 The ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {PolyFun}(\mathcal {S})$ is the underlying
$\operatorname {PolyFun}(\mathcal {S})$ is the underlying ![]() $(\infty,2)$-category of the double
$(\infty,2)$-category of the double ![]() $\infty$-category of polynomial functors considered in [Reference Gepner, Haugseng and KockGHK22].
$\infty$-category of polynomial functors considered in [Reference Gepner, Haugseng and KockGHK22].
Corollary 3.3.5 The functor ![]() ${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ restricts to an equivalence
${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ restricts to an equivalence
Proof. We apply the description from Corollary 2.5.18 to understand ![]() ${\text {Sl}}$: on objects,
${\text {Sl}}$: on objects, ![]() ${\text {Sl}}$ takes
${\text {Sl}}$ takes ![]() $X \in \mathcal {S}$ to the
$X \in \mathcal {S}$ to the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {S}_{/X}$, and on morphisms it takes the bispan
$\mathcal {S}_{/X}$, and on morphisms it takes the bispan
to the functor ![]() $t_{!}p_{*}s^{*}$. The functors of this form are precisely the polynomial functors, by [Reference Gepner, Haugseng and KockGHK22, Theorem 2.2.3]. The description of
$t_{!}p_{*}s^{*}$. The functors of this form are precisely the polynomial functors, by [Reference Gepner, Haugseng and KockGHK22, Theorem 2.2.3]. The description of ![]() ${\text {Sl}}$ on 2-morphisms from Corollary 2.5.18(3) implies that they are sent to composites of equivalences and (co)unit transformations that are cartesian by [Reference Gepner, Haugseng and KockGHK22, Lemma 2.1.5]. Hence,
${\text {Sl}}$ on 2-morphisms from Corollary 2.5.18(3) implies that they are sent to composites of equivalences and (co)unit transformations that are cartesian by [Reference Gepner, Haugseng and KockGHK22, Lemma 2.1.5]. Hence, ![]() ${\text {Sl}}$ factors through
${\text {Sl}}$ factors through ![]() $\operatorname {PolyFun}(\mathcal {S})$, and is essentially surjective on objects and morphisms. To show that
$\operatorname {PolyFun}(\mathcal {S})$, and is essentially surjective on objects and morphisms. To show that ![]() ${\text {Sl}}$ factors through an equivalence it then suffices to show it gives an equivalence
${\text {Sl}}$ factors through an equivalence it then suffices to show it gives an equivalence
on mapping ![]() $\infty$-categories for all
$\infty$-categories for all ![]() $X,Y$ in
$X,Y$ in ![]() $\mathcal {S}$. Using Corollary 2.3.18 we can identify this with the functor shown to be an equivalence in [Reference Gepner, Haugseng and KockGHK22, Proposition 2.4.13].
$\mathcal {S}$. Using Corollary 2.3.18 we can identify this with the functor shown to be an equivalence in [Reference Gepner, Haugseng and KockGHK22, Proposition 2.4.13].
Remark 3.3.6 We expect that there is an analogue of Corollary 3.3.5 for bispans in any ![]() $\infty$-topos
$\infty$-topos ![]() $\mathcal {X}$, but this requires working with internal
$\mathcal {X}$, but this requires working with internal ![]() $\infty$-categories in
$\infty$-categories in ![]() $\mathcal {X}$ (or, equivalently, sheaves of
$\mathcal {X}$ (or, equivalently, sheaves of ![]() $\infty$-categories on
$\infty$-categories on ![]() $\mathcal {X}$): a key step in the identification of polynomial functors with bispans is the description of colimit-preserving functors between slices of
$\mathcal {X}$): a key step in the identification of polynomial functors with bispans is the description of colimit-preserving functors between slices of ![]() $\mathcal {S}$ as spans, i.e. the equivalence
$\mathcal {S}$ as spans, i.e. the equivalence
This certainly fails for any other ![]() $\infty$-topos
$\infty$-topos ![]() $\mathcal {X}$, but an analogous statement should hold if we view
$\mathcal {X}$, but an analogous statement should hold if we view ![]() $\mathcal {X}$ instead as an
$\mathcal {X}$ instead as an ![]() $\infty$-category internal to itself.
$\infty$-category internal to itself.
Definition 3.3.7 An analytic functor ![]() $F \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$ is a functor that preserves sifted colimits and weakly contractible limits. By [Reference Gepner, Haugseng and KockGHK22, Proposition 3.1.9] the analytic functors are equivalently those functors obtained as composites
$F \colon \mathcal {S}_{/X} \to \mathcal {S}_{/Y}$ is a functor that preserves sifted colimits and weakly contractible limits. By [Reference Gepner, Haugseng and KockGHK22, Proposition 3.1.9] the analytic functors are equivalently those functors obtained as composites ![]() $t_{!}p_{*}s^{*}$ for some bispan of spaces
$t_{!}p_{*}s^{*}$ for some bispan of spaces
where ![]() $p$ has finite discrete fibres.
$p$ has finite discrete fibres.
As a consequence, we obtain the following.
Corollary 3.3.8 The functor ![]() ${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ factors through an equivalence
${\text {Sl}} \colon {\text {BISPAN}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ factors through an equivalence
where ![]() $\operatorname {AnFun}(\mathcal {S})$ is the locally full sub-
$\operatorname {AnFun}(\mathcal {S})$ is the locally full sub-![]() $(\infty,2)$-category of
$(\infty,2)$-category of ![]() $\operatorname {PolyFun}(\mathcal {S})$ containing all objects, with the analytic functors as morphisms, as well as all 2-morphisms between these.
$\operatorname {PolyFun}(\mathcal {S})$ containing all objects, with the analytic functors as morphisms, as well as all 2-morphisms between these.
Definition 3.3.9 An analytic monad is a monad in the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() $\operatorname {AnFun}(\mathcal {S})$, i.e. an associative algebra in the monoidal
$\operatorname {AnFun}(\mathcal {S})$, i.e. an associative algebra in the monoidal ![]() $\infty$-category
$\infty$-category ![]() ${\text {MAP}}_{\operatorname {AnFun}(\mathcal {S})}(X,X)$ of endomorphisms of some object
${\text {MAP}}_{\operatorname {AnFun}(\mathcal {S})}(X,X)$ of endomorphisms of some object ![]() $X$, or a functor
$X$, or a functor ![]() $\mathfrak {mnd} \to \operatorname {AnFun}(\mathcal {S})$, where
$\mathfrak {mnd} \to \operatorname {AnFun}(\mathcal {S})$, where ![]() $\mathfrak {mnd}$ is the universal 2-category containing a monad. In other words, it is a monad on the
$\mathfrak {mnd}$ is the universal 2-category containing a monad. In other words, it is a monad on the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {S}_{/X}$ whose underlying endofunctor is analytic and whose unit and multiplication transformations are cartesian. From the equivalence (39) we see that analytic monads are equivalently monads in the
$\mathcal {S}_{/X}$ whose underlying endofunctor is analytic and whose unit and multiplication transformations are cartesian. From the equivalence (39) we see that analytic monads are equivalently monads in the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S})$.
${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S})$.
Corollary 3.3.10 Suppose ![]() $T$ is an analytic monad on
$T$ is an analytic monad on ![]() $\mathcal {S}_{/X}$ and
$\mathcal {S}_{/X}$ and ![]() $\mathcal {V}$ is a symmetric monoidal
$\mathcal {V}$ is a symmetric monoidal ![]() $\infty$-category compatible with
$\infty$-category compatible with ![]() $\infty$-groupoid-indexed colimits. Then
$\infty$-groupoid-indexed colimits. Then ![]() $T$ induces a canonical monad
$T$ induces a canonical monad ![]() $T_{\mathcal {V}}$ on
$T_{\mathcal {V}}$ on ![]() ${\text {Fun}}(X, \mathcal {V})$.
${\text {Fun}}(X, \mathcal {V})$.
Proof. We can identify ![]() $T$ with a monad on
$T$ with a monad on ![]() $X \in {\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S})$. By Corollary 3.2.9
$X \in {\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S})$. By Corollary 3.2.9 ![]() $\mathcal {V}$ induces a functor
$\mathcal {V}$ induces a functor ![]() ${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ that takes
${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S}) \to {\text {CAT}}_{\infty }$ that takes ![]() $Y \in \mathcal {S}$ to
$Y \in \mathcal {S}$ to ![]() ${\text {Fun}}(Y, \mathcal {V})$. Any functor of
${\text {Fun}}(Y, \mathcal {V})$. Any functor of ![]() $(\infty,2)$-categories preserves monads, since they can be described as simply functors of
$(\infty,2)$-categories preserves monads, since they can be described as simply functors of ![]() $(\infty,2)$-categories from
$(\infty,2)$-categories from ![]() $\mathfrak {mnd}$. Hence under the functor induced by
$\mathfrak {mnd}$. Hence under the functor induced by ![]() $\mathcal {V}$ the monad
$\mathcal {V}$ the monad ![]() $T$ maps to a monad in
$T$ maps to a monad in ![]() ${\text {CAT}}_{\infty }$ which indeed acts on
${\text {CAT}}_{\infty }$ which indeed acts on ![]() ${\text {Fun}}(X, \mathcal {V})$.
${\text {Fun}}(X, \mathcal {V})$.
Remark 3.3.11 Suppose the underlying bispan of the monad ![]() $T$ is
$T$ is
Then the underlying endofunctor of the monad ![]() $T_{\mathcal {V}}$ is given by
$T_{\mathcal {V}}$ is given by
This has the same form as the formula for the free algebra monad of an ![]() $\infty$-operad, and the main result of [Reference Gepner, Haugseng and KockGHK22] is that analytic monads are equivalent to
$\infty$-operad, and the main result of [Reference Gepner, Haugseng and KockGHK22] is that analytic monads are equivalent to ![]() $\infty$-operads in the form of dendroidal Segal spaces. We therefore expect that if
$\infty$-operads in the form of dendroidal Segal spaces. We therefore expect that if ![]() $\mathcal {O}$ is the
$\mathcal {O}$ is the ![]() $\infty$-operad corresponding to
$\infty$-operad corresponding to ![]() $T$, then the monad
$T$, then the monad ![]() $T_{\mathcal {V}}$ is the free
$T_{\mathcal {V}}$ is the free ![]() $\mathcal {O}$-algebra monad for
$\mathcal {O}$-algebra monad for ![]() $\mathcal {O}$-algebras in
$\mathcal {O}$-algebras in ![]() $\mathcal {V}$.
$\mathcal {V}$.
3.4 Equivariant bispans and  $G$-symmetric monoidal
$G$-symmetric monoidal  $\infty$-categories
$\infty$-categories
In this section we look at the ![]() $G$-equivariant version of our results from § 3.1 on symmetric monoidal
$G$-equivariant version of our results from § 3.1 on symmetric monoidal ![]() $\infty$-categories compatible with finite coproducts, where
$\infty$-categories compatible with finite coproducts, where ![]() $G$ is a finite group: we replace the category of finite sets by the category
$G$ is a finite group: we replace the category of finite sets by the category ![]() $\mathbb {F}_{G}$ of finite
$\mathbb {F}_{G}$ of finite ![]() $G$-sets, and consider when a
$G$-sets, and consider when a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category, defined as a product-preserving functor
$\infty$-category, defined as a product-preserving functor ![]() $\operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$, is distributive, and so extends to a functor
$\operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$, is distributive, and so extends to a functor ![]() ${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$.
${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$.
Definition 3.4.1 Let ![]() $G$ be a finite group, and
$G$ be a finite group, and ![]() $BG$ the corresponding 1-object groupoid. We write
$BG$ the corresponding 1-object groupoid. We write ![]() $\mathbb {F}_{G}$ for the category
$\mathbb {F}_{G}$ for the category ![]() ${\text {Fun}}(BG, \mathbb {F})$ of finite
${\text {Fun}}(BG, \mathbb {F})$ of finite ![]() $G$-sets, and
$G$-sets, and ![]() $\mathcal {O}_{G}$ for the full subcategory of orbits, i.e. finite
$\mathcal {O}_{G}$ for the full subcategory of orbits, i.e. finite ![]() $G$-sets of the form
$G$-sets of the form ![]() $G/H$ where
$G/H$ where ![]() $H$ is a subgroup of
$H$ is a subgroup of ![]() $G$. Then
$G$. Then ![]() $\mathbb {F}_{G}$ is obtained from
$\mathbb {F}_{G}$ is obtained from ![]() $\mathcal {O}_{G}$ by freely adding finite coproducts, so that for any
$\mathcal {O}_{G}$ by freely adding finite coproducts, so that for any ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ with finite products, restriction along the inclusion
$\mathcal {C}$ with finite products, restriction along the inclusion ![]() $\mathcal {O}_{G} \hookrightarrow \mathbb {F}_{G}$ gives an equivalence
$\mathcal {O}_{G} \hookrightarrow \mathbb {F}_{G}$ gives an equivalence
If ![]() $\mathcal {C}$ is the
$\mathcal {C}$ is the ![]() $\infty$-category of spaces, this says that the
$\infty$-category of spaces, this says that the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {S}_{G} := \mathcal {P}(\mathcal {O}_{G})$ of
$\mathcal {S}_{G} := \mathcal {P}(\mathcal {O}_{G})$ of ![]() $G$-spaces Footnote 12 is equivalent to
$G$-spaces Footnote 12 is equivalent to ![]() ${\text {Fun}}^{\times }(\mathbb {F}_{G}^{{\text {op}}}, \mathcal {S})$. By analogy with the case of
${\text {Fun}}^{\times }(\mathbb {F}_{G}^{{\text {op}}}, \mathcal {S})$. By analogy with the case of ![]() $G$-spaces, we can think of a functor
$G$-spaces, we can think of a functor ![]() $\mathcal {F} \colon \mathcal {O}_{G}^{{\text {op}}} \to \mathcal {C}$ as an ‘object of
$\mathcal {F} \colon \mathcal {O}_{G}^{{\text {op}}} \to \mathcal {C}$ as an ‘object of ![]() $\mathcal {C}$ with
$\mathcal {C}$ with ![]() $G$-action’, with
$G$-action’, with ![]() $\mathcal {F}^{H}:= \mathcal {F}(G/H)$ the object of ‘
$\mathcal {F}^{H}:= \mathcal {F}(G/H)$ the object of ‘![]() $H$-fixed points’ of
$H$-fixed points’ of ![]() $\mathcal {F}$. We will, in particular, apply this notation for functors
$\mathcal {F}$. We will, in particular, apply this notation for functors ![]() $\mathcal {O}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$, which we will call
$\mathcal {O}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$, which we will call ![]() $G$-
$G$- ![]() $\infty$-categories.
$\infty$-categories.
Remark 3.4.2 The category ![]() $\mathbb {F}_{G}$ is extensive, and so by [Reference BarwickBar17, Proposition 4.3] the coproduct in
$\mathbb {F}_{G}$ is extensive, and so by [Reference BarwickBar17, Proposition 4.3] the coproduct in ![]() $\mathbb {F}_{G}$ gives both the product and coproduct in
$\mathbb {F}_{G}$ gives both the product and coproduct in ![]() $\operatorname {Span}(\mathbb {F}_{G})$.
$\operatorname {Span}(\mathbb {F}_{G})$.
Definition 3.4.3 Let ![]() $\mathcal {C}$ be an
$\mathcal {C}$ be an ![]() $\infty$-category with finite products. A
$\infty$-category with finite products. A ![]() $G$-commutative monoid in
$G$-commutative monoid in ![]() $\mathcal {C}$ is a product-preserving functor
$\mathcal {C}$ is a product-preserving functor ![]() $\operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {C}$. We write
$\operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {C}$. We write
for the ![]() $\infty$-category of
$\infty$-category of ![]() $G$-commutative monoids in
$G$-commutative monoids in ![]() $\mathcal {C}$. A
$\mathcal {C}$. A ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category is a
$\infty$-category is a ![]() $G$-commutative monoid in
$G$-commutative monoid in ![]() ${\text {Cat}}_\infty$.
${\text {Cat}}_\infty$.
Remark 3.4.4 When ![]() $G$ is the trivial group this is equivalent to the usual definition of commutative monoids (in terms of functors from
$G$ is the trivial group this is equivalent to the usual definition of commutative monoids (in terms of functors from ![]() $\mathbb {F}_{*}$ satisfying a Segal condition) by Proposition 3.1.5. More generally, see [Reference NardinNar16, Theorem 6.5] for an alternative description of
$\mathbb {F}_{*}$ satisfying a Segal condition) by Proposition 3.1.5. More generally, see [Reference NardinNar16, Theorem 6.5] for an alternative description of ![]() $G$-commutative monoids in terms of ‘finite pointed
$G$-commutative monoids in terms of ‘finite pointed ![]() $G$-sets’ (where this must be read in a non-trivial parametrized sense).
$G$-sets’ (where this must be read in a non-trivial parametrized sense).
Remark 3.4.5 A functor ![]() $\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {C}$ preserves products if and only if the restriction to
$\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to \mathcal {C}$ preserves products if and only if the restriction to ![]() $\mathbb {F}_{G}^{{\text {op}}} \to \mathcal {C}$ preserves products, and so is determined by its restriction to
$\mathbb {F}_{G}^{{\text {op}}} \to \mathcal {C}$ preserves products, and so is determined by its restriction to ![]() $\mathcal {O}_{G}^{{\text {op}}} \to \mathcal {C}$. The additional structure given by the forwards maps in
$\mathcal {O}_{G}^{{\text {op}}} \to \mathcal {C}$. The additional structure given by the forwards maps in ![]() $\operatorname {Span}(\mathbb {F}_{G})$ can be decomposed into:
$\operatorname {Span}(\mathbb {F}_{G})$ can be decomposed into:
• multiplication maps
 $\mathcal {F}^{H} \times \mathcal {F}^{H} \to \mathcal {F}^{H}$ for each subgroup
$\mathcal {F}^{H} \times \mathcal {F}^{H} \to \mathcal {F}^{H}$ for each subgroup  $H$ of
$H$ of  $G$, coming from the fold map
$G$, coming from the fold map  $G/H \amalg G/H \to G/H$;
$G/H \amalg G/H \to G/H$;• multiplicative transfer maps
 $\mathcal {F}^{H} \to \mathcal {F}^{K}$ for each inclusion
$\mathcal {F}^{H} \to \mathcal {F}^{K}$ for each inclusion  $H \subseteq K$ of subgroups, coming from the quotient map
$H \subseteq K$ of subgroups, coming from the quotient map  $G/H \to G/K$;
$G/H \to G/K$;
together with various homotopy-coherent compatibilities that, in particular, make each ![]() $\mathcal {F}^{H}$ a commutative monoid.
$\mathcal {F}^{H}$ a commutative monoid.
Remark 3.4.6 Grouplike ![]() $G$-commutative monoids in
$G$-commutative monoids in ![]() $\mathcal {S}$ can be identified with connective genuine
$\mathcal {S}$ can be identified with connective genuine ![]() $G$-spectra, by [Reference NardinNar16, Corollary A.4.1]. Applying
$G$-spectra, by [Reference NardinNar16, Corollary A.4.1]. Applying ![]() $\pi _{0}$, such a grouplike
$\pi _{0}$, such a grouplike ![]() $G$-commutative monoid induces a
$G$-commutative monoid induces a ![]() $G$-commutative monoid in
$G$-commutative monoid in ![]() ${\text {Set}}$, which factors through a product-preserving functor
${\text {Set}}$, which factors through a product-preserving functor
because it is grouplike. This is precisely a Mackey functor, which is well-known as the structure appearing as ![]() $\pi _{0}$ of a genuine
$\pi _{0}$ of a genuine ![]() $G$-spectrum.
$G$-spectrum.
For a functor ![]() $\operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ we can simplify the condition that it is left adjointable as follows.
$\operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ we can simplify the condition that it is left adjointable as follows.
Proposition 3.4.7 Suppose ![]() $\mathcal {F} \colon \mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ is a product-preserving functor. Then
$\mathcal {F} \colon \mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ is a product-preserving functor. Then ![]() $\mathcal {F}$ is left adjointable if and only if:
$\mathcal {F}$ is left adjointable if and only if:
(1) for every subgroup
 $H \subseteq G$, the
$H \subseteq G$, the  $\infty$-category
$\infty$-category  $\mathcal {F}^{H}$ has finite coproducts;
$\mathcal {F}^{H}$ has finite coproducts;(2) for every inclusion of subgroups
 $H \subseteq K$ the functor
$H \subseteq K$ the functor  $(q_{H}^{K})^{\circledast } \colon \mathcal {F}^{K} \to \mathcal {F}^{H}$, corresponding to the quotient map
$(q_{H}^{K})^{\circledast } \colon \mathcal {F}^{K} \to \mathcal {F}^{H}$, corresponding to the quotient map  $q_{H}^{K} \colon G/H \to G/K$, has a left adjoint
$q_{H}^{K} \colon G/H \to G/K$, has a left adjoint  $(q_{H}^{K})_{\oplus }$;
$(q_{H}^{K})_{\oplus }$;(3) for every inclusion of subgroups
 $H \subseteq K$ the functor
$H \subseteq K$ the functor  $(q_{H}^{K})^{\circledast }$ preserves finite coproducts;
$(q_{H}^{K})^{\circledast }$ preserves finite coproducts;(4) for subgroups
 $H,K \subseteq L$, let
$H,K \subseteq L$, let  $X$ be defined by the pullback
then the square
$X$ be defined by the pullback
then the square is left adjointable, i.e. the mate transformation
is left adjointable, i.e. the mate transformation is an equivalence.
is an equivalence. \[ f_{K,\oplus}f_{H}^{\circledast} \to (q^{L}_{K})^{\circledast}(q^{L}_{H})_{\oplus} \]
\[ f_{K,\oplus}f_{H}^{\circledast} \to (q^{L}_{K})^{\circledast}(q^{L}_{H})_{\oplus} \]
Remark 3.4.8 The pullback ![]() $X$ in condition (4) can be decomposed into a sum of orbits indexed by double cosets:
$X$ in condition (4) can be decomposed into a sum of orbits indexed by double cosets:
where ![]() $K_{g}$ denotes the conjugate
$K_{g}$ denotes the conjugate ![]() $g K g^{-1}$. The left adjointability in condition (4) then amounts to the following double coset formula:
$g K g^{-1}$. The left adjointability in condition (4) then amounts to the following double coset formula:
where ![]() $c_{g}$ is the isomorphism
$c_{g}$ is the isomorphism ![]() $G/K \cong G/K_{g}$.
$G/K \cong G/K_{g}$.
Proof of Proposition 3.4.7 Since ![]() $\mathbb {F}_{G}$ is extensive, a morphism
$\mathbb {F}_{G}$ is extensive, a morphism ![]() $\phi \colon X \to Y$ in
$\phi \colon X \to Y$ in ![]() $\mathbb {F}_{G}$ where
$\mathbb {F}_{G}$ where ![]() $Y \cong \coprod _{i} G/H_{i}$ decomposes as a coproduct
$Y \cong \coprod _{i} G/H_{i}$ decomposes as a coproduct ![]() $\coprod _{i} \phi _{i}$ for
$\coprod _{i} \phi _{i}$ for ![]() $\phi _{i} \colon X_{i} \to G/H_{i}$. Since
$\phi _{i} \colon X_{i} \to G/H_{i}$. Since ![]() $\mathcal {F}$ is product-preserving, to show that
$\mathcal {F}$ is product-preserving, to show that ![]() $\phi ^{\circledast }$ has a left adjoint it suffices to consider the case where
$\phi ^{\circledast }$ has a left adjoint it suffices to consider the case where ![]() $Y$ is an orbit
$Y$ is an orbit ![]() $G/H$. Moreover, for
$G/H$. Moreover, for ![]() $\phi \colon X \to G/H$ where
$\phi \colon X \to G/H$ where ![]() $X \cong \coprod _{j} G/K_{j}$ we can decompose
$X \cong \coprod _{j} G/K_{j}$ we can decompose ![]() $\phi$ as
$\phi$ as
 \[ \coprod_{j} G/K_{j} \xrightarrow{\coprod_{j} \phi|_{G/K_{j}}} \coprod_{j} G/H \xrightarrow{\nabla} G/H, \]
\[ \coprod_{j} G/K_{j} \xrightarrow{\coprod_{j} \phi|_{G/K_{j}}} \coprod_{j} G/H \xrightarrow{\nabla} G/H, \]
where ![]() $\nabla$ denotes the fold map. Since adjunctions compose, to prove that left adjoints exist it is enough to consider fold maps and morphisms between orbits. In the first case, the functor
$\nabla$ denotes the fold map. Since adjunctions compose, to prove that left adjoints exist it is enough to consider fold maps and morphisms between orbits. In the first case, the functor ![]() $\nabla ^{\circledast }$ induced by the fold map
$\nabla ^{\circledast }$ induced by the fold map ![]() $\nabla \colon \coprod _{j \in J} G/H \to G/H$ can be identified with the diagonal functor
$\nabla \colon \coprod _{j \in J} G/H \to G/H$ can be identified with the diagonal functor ![]() $\mathcal {F}^{H} \to {\text {Fun}}(J, \mathcal {F}^{H})$ and so has a left adjoint for all finite sets
$\mathcal {F}^{H} \to {\text {Fun}}(J, \mathcal {F}^{H})$ and so has a left adjoint for all finite sets ![]() $J$ if and only if
$J$ if and only if ![]() $\mathcal {F}^{H}$ admits finite coproducts, i.e. if and only if assumption (1) holds. In the second case, a morphism
$\mathcal {F}^{H}$ admits finite coproducts, i.e. if and only if assumption (1) holds. In the second case, a morphism ![]() $\phi \colon G/K \to G/H$ can be decomposed as
$\phi \colon G/K \to G/H$ can be decomposed as ![]() $G/K \xrightarrow {\sim } G/gKg^{-1} \xrightarrow {q_{gKg^{-1}}^{H}} G/H$ and so
$G/K \xrightarrow {\sim } G/gKg^{-1} \xrightarrow {q_{gKg^{-1}}^{H}} G/H$ and so ![]() $\phi ^{\circledast }$ has a left adjoint for all such maps
$\phi ^{\circledast }$ has a left adjoint for all such maps ![]() $\phi$ if and only if assumption (2) holds.
$\phi$ if and only if assumption (2) holds.
Now we consider the adjointability condition. Again using that ![]() $\mathbb {F}_{G}$ is extensive, a pullback square
$\mathbb {F}_{G}$ is extensive, a pullback square

where ![]() $W \cong \coprod _{i} G/H_{i}$ decomposes as a coproduct of pullback squares
$W \cong \coprod _{i} G/H_{i}$ decomposes as a coproduct of pullback squares

Since ![]() $\mathcal {F}$ preserves products and taking mate squares commutes with products, we see that
$\mathcal {F}$ preserves products and taking mate squares commutes with products, we see that ![]() $\mathcal {F}$ is left adjointable if and only if it is left adjointable for pullback squares
$\mathcal {F}$ is left adjointable if and only if it is left adjointable for pullback squares

over an orbit. If ![]() $Y \cong \coprod _{i} G/K_{i}$ and
$Y \cong \coprod _{i} G/K_{i}$ and ![]() $Z \cong \coprod _{j} G/L_{j}$, then we can decompose our pullback square into the diagram
$Z \cong \coprod _{j} G/L_{j}$, then we can decompose our pullback square into the diagram

where the top left square decomposes as a coproduct of pullback squares

of the form considered in condition (4) and the other squares are defined using fold maps. Since mate squares are compatible with both vertical and horizontal composition of squares, the functor ![]() $\mathcal {F}$ will be left adjointable if the images of the four squares in such decompositions are left adjointable. Using again the assumption that
$\mathcal {F}$ will be left adjointable if the images of the four squares in such decompositions are left adjointable. Using again the assumption that ![]() $\mathcal {F}$ preserves finite products, we see that this holds if and only if condition (4) holds and we have left adjointability for squares of the form
$\mathcal {F}$ preserves finite products, we see that this holds if and only if condition (4) holds and we have left adjointability for squares of the form

The latter means the canonical map ![]() $\nabla _{K,\oplus }(\prod _{i} \phi ^{\circledast }) \to \phi ^{\circledast }\nabla _{H,\oplus }$ is an equivalence, i.e. the functor
$\nabla _{K,\oplus }(\prod _{i} \phi ^{\circledast }) \to \phi ^{\circledast }\nabla _{H,\oplus }$ is an equivalence, i.e. the functor ![]() $\phi ^{\circledast }$ preserves
$\phi ^{\circledast }$ preserves ![]() $I$-indexed coproducts where
$I$-indexed coproducts where ![]() $\phi$ is a map between orbits in
$\phi$ is a map between orbits in ![]() $\mathbb {F}_{G}$. Since such maps are composites of isomorphisms and maps coming from subgroup inclusions, this is equivalent to condition (3).
$\mathbb {F}_{G}$. Since such maps are composites of isomorphisms and maps coming from subgroup inclusions, this is equivalent to condition (3).
Definition 3.4.9 We say a ![]() $G$-
$G$-![]() $\infty$-category
$\infty$-category ![]() $\mathcal {F}$ has additive transfers if it satisfies the conditions of Proposition 3.4.7 when viewed as a product-preserving functor
$\mathcal {F}$ has additive transfers if it satisfies the conditions of Proposition 3.4.7 when viewed as a product-preserving functor ![]() $\mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$.
$\mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$.
Remark 3.4.10 In the terminology of [Reference ShahSha23, Reference NardinNar16] a ![]() $G$-
$G$-![]() $\infty$-category has finite
$\infty$-category has finite ![]() $G$-coproducts if and only if it has additive transfers in our sense, cf. [Reference NardinNar16, Proposition 2.11].
$G$-coproducts if and only if it has additive transfers in our sense, cf. [Reference NardinNar16, Proposition 2.11].
Proposition 3.4.11 Suppose ![]() $\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ is a
$\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ is a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category whose underlying
$\infty$-category whose underlying ![]() $G$-
$G$-![]() $\infty$-category has additive transfers. Then
$\infty$-category has additive transfers. Then ![]() $\mathcal {F}$ is distributive if and only if for all morphisms
$\mathcal {F}$ is distributive if and only if for all morphisms ![]() $\phi \colon X \to Y, \psi \colon Y \to G/H$ in
$\phi \colon X \to Y, \psi \colon Y \to G/H$ in ![]() $\mathbb {F}_{G}$, the distributivity transformation
$\mathbb {F}_{G}$, the distributivity transformation
from the distributivity square

is an equivalence.
Remark 3.4.12 Decomposing ![]() $Z = \psi _{*}X$ in such a distributivity diagram as a coproduct of orbits is often a non-trivial problem in finite group theory, so we do not expect that this distributivity condition can be simplified further in general.
$Z = \psi _{*}X$ in such a distributivity diagram as a coproduct of orbits is often a non-trivial problem in finite group theory, so we do not expect that this distributivity condition can be simplified further in general.
Proof of Proposition 3.4.11 Since ![]() $\mathbb {F}_{G}$ is extensive, we know from Example 2.6.12 that finite coproducts of distributivity diagrams are again distributivity diagrams. Since
$\mathbb {F}_{G}$ is extensive, we know from Example 2.6.12 that finite coproducts of distributivity diagrams are again distributivity diagrams. Since ![]() $\mathcal {F}$ preserves products, distributivity transformations associated to such coproducts decompose as products, hence the distributivity condition reduces to the case where the target of the second map is an orbit.
$\mathcal {F}$ preserves products, distributivity transformations associated to such coproducts decompose as products, hence the distributivity condition reduces to the case where the target of the second map is an orbit.
Definition 3.4.13 We say a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ is compatible with additive transfers if it satisfies the condition of Proposition 3.4.11.
$\mathcal {F} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ is compatible with additive transfers if it satisfies the condition of Proposition 3.4.11.
Corollary 3.4.14 Product-preserving functors ![]() ${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ correspond to
${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ correspond to ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories that are compatible with additive transfers.
$\infty$-categories that are compatible with additive transfers.
Proof. By Theorem 2.5.1, functors ![]() ${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$ correspond to distributive functors
${\text {BISPAN}}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$ correspond to distributive functors ![]() $\operatorname {Span}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$. Moreover, from Remark 2.6.13 we know that the product in
$\operatorname {Span}(\mathbb {F}_{G}) \to {\text {CAT}}_{\infty }$. Moreover, from Remark 2.6.13 we know that the product in ![]() ${\text {BISPAN}}(\mathbb {F}_{G})$ is given by the coproduct in
${\text {BISPAN}}(\mathbb {F}_{G})$ is given by the coproduct in ![]() $\mathbb {F}_{G}$, just as in
$\mathbb {F}_{G}$, just as in ![]() $\operatorname {Span}(\mathbb {F}_{G})$, so product-preserving functors from
$\operatorname {Span}(\mathbb {F}_{G})$, so product-preserving functors from ![]() ${\text {BISPAN}}(\mathbb {F}_{G})$ correspond to product-preserving distributive functors under this equivalence. By Propositions 3.4.7 and 3.4.11, the latter are equivalent to
${\text {BISPAN}}(\mathbb {F}_{G})$ correspond to product-preserving distributive functors under this equivalence. By Propositions 3.4.7 and 3.4.11, the latter are equivalent to ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories that are compatible with additive transfers.
$\infty$-categories that are compatible with additive transfers.
We now consider some examples of ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories compatible with additive transfers.
$\infty$-categories compatible with additive transfers.
Example 3.4.15 (Finite  $G$-sets)
$G$-sets)
As a special case of Proposition 3.3.1 we get a functor
taking ![]() $X \in \mathbb {F}_{G}$ to the slice
$X \in \mathbb {F}_{G}$ to the slice ![]() $(\mathbb {F}_{G})_{/X}$. Here we can identify
$(\mathbb {F}_{G})_{/X}$. Here we can identify ![]() $(\mathbb {F}_{G})_{/(G/H)}$ with
$(\mathbb {F}_{G})_{/(G/H)}$ with ![]() $\mathbb {F}_{H}$, so the underlying
$\mathbb {F}_{H}$, so the underlying ![]() $G$-category is given by
$G$-category is given by ![]() $(G/H) \mapsto \mathbb {F}_{H}$. Since
$(G/H) \mapsto \mathbb {F}_{H}$. Since ![]() $\mathbb {F}_{G}$ is extensive, this is a product-preserving functor; the underlying
$\mathbb {F}_{G}$ is extensive, this is a product-preserving functor; the underlying ![]() $G$-symmetric monoidal category encodes the cartesian products of finite
$G$-symmetric monoidal category encodes the cartesian products of finite ![]() $G$-sets and their compatibility with the left and right adjoints to the restriction functor
$G$-sets and their compatibility with the left and right adjoints to the restriction functor ![]() $\mathbb {F}_{G} \to \mathbb {F}_{H}$ for
$\mathbb {F}_{G} \to \mathbb {F}_{H}$ for ![]() $H$ a subgroup of
$H$ a subgroup of ![]() $G$.
$G$.
Example 3.4.16 ( $G$-spaces)
$G$-spaces)
As a variant of the previous example, we can consider the ![]() $G$-
$G$-![]() $\infty$-category of
$\infty$-category of ![]() $G$-spaces. Since
$G$-spaces. Since ![]() $\mathcal {S}_{G}$ is locally cartesian closed (being a (presheaf)
$\mathcal {S}_{G}$ is locally cartesian closed (being a (presheaf) ![]() $\infty$-topos), we can apply Proposition 3.3.1 to it and then restrict to bispans in
$\infty$-topos), we can apply Proposition 3.3.1 to it and then restrict to bispans in ![]() $\mathbb {F}_{G}$ to get a functor
$\mathbb {F}_{G}$ to get a functor
that takes ![]() $X \in \mathbb {F}_{G}$ to
$X \in \mathbb {F}_{G}$ to ![]() $(\mathcal {S}_{G})_{/X}$; here we can identify
$(\mathcal {S}_{G})_{/X}$; here we can identify ![]() $(\mathcal {S}_{G})_{/(G/H)}$ with
$(\mathcal {S}_{G})_{/(G/H)}$ with ![]() $\mathcal {S}_{H}$. Since
$\mathcal {S}_{H}$. Since ![]() $\mathcal {S}_{G}$ is extensive, this is a product-preserving functor. The underlying
$\mathcal {S}_{G}$ is extensive, this is a product-preserving functor. The underlying ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category (compatible with additive transfers) encodes the cartesian products of
$\infty$-category (compatible with additive transfers) encodes the cartesian products of ![]() $H$-spaces for all subgroups
$H$-spaces for all subgroups ![]() $H$ of
$H$ of ![]() $G$ and their compatibility with the left and right adjoints to the restriction functor
$G$ and their compatibility with the left and right adjoints to the restriction functor ![]() $\mathcal {S}_{G} \to \mathcal {S}_{H}$.
$\mathcal {S}_{G} \to \mathcal {S}_{H}$.
Example 3.4.17 ( $G$-actions in a symmetric monoidal
$G$-actions in a symmetric monoidal  $\infty$-category)
$\infty$-category)
Let ![]() $\mathcal {C}$ be a symmetric monoidal
$\mathcal {C}$ be a symmetric monoidal ![]() $\infty$-category. By Proposition 3.2.3 this determines a functor
$\infty$-category. By Proposition 3.2.3 this determines a functor ![]() $\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ taking
$\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}) \to {\text {Cat}}_\infty$ taking ![]() $X \in \mathcal {S}$ to
$X \in \mathcal {S}$ to ![]() ${\text {Fun}}(X, \mathcal {C})$. For a finite group
${\text {Fun}}(X, \mathcal {C})$. For a finite group ![]() $G$ we have a functor
$G$ we have a functor ![]() $\mathcal {G} \colon \mathbb {F}_{G} \to \mathcal {S}$ by restricting the colimit functor
$\mathcal {G} \colon \mathbb {F}_{G} \to \mathcal {S}$ by restricting the colimit functor ![]() ${\text {Fun}}(BG, \mathcal {S}) \to \mathcal {S}$; this takes a finite
${\text {Fun}}(BG, \mathcal {S}) \to \mathcal {S}$; this takes a finite ![]() $G$-set
$G$-set ![]() $X$ to the groupoid
$X$ to the groupoid ![]() $X/\!/G = X_{hG}$. The functor
$X/\!/G = X_{hG}$. The functor ![]() $\mathcal {G}$ preserves pullbacks since the colimit functor factors as the straightening equivalence
$\mathcal {G}$ preserves pullbacks since the colimit functor factors as the straightening equivalence ![]() ${\text {Fun}}(BG, \mathcal {S}) \xrightarrow {\sim } \mathcal {S}_{/BG}$ followed by the forgetful functor to
${\text {Fun}}(BG, \mathcal {S}) \xrightarrow {\sim } \mathcal {S}_{/BG}$ followed by the forgetful functor to ![]() $\mathcal {S}$, which preserves all weakly contractible limits. Moreover,
$\mathcal {S}$, which preserves all weakly contractible limits. Moreover, ![]() $\mathcal {G}$ takes values in
$\mathcal {G}$ takes values in ![]() $\mathcal {S}_{\mathrm {fin}}$, and so yields a functor
$\mathcal {S}_{\mathrm {fin}}$, and so yields a functor ![]() $\operatorname {Span}(\mathcal {G})\colon \operatorname {Span}(\mathbb {F}_{G}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$. This functor preserves products, since
$\operatorname {Span}(\mathcal {G})\colon \operatorname {Span}(\mathbb {F}_{G}) \to \operatorname {Span}_{\mathrm {fin}}(\mathcal {S})$. This functor preserves products, since ![]() $\mathcal {G}$ preserves coproducts. It follows that we can restrict along
$\mathcal {G}$ preserves coproducts. It follows that we can restrict along ![]() $\operatorname {Span}(\mathcal {G})$ and obtain for any symmetric monoidal
$\operatorname {Span}(\mathcal {G})$ and obtain for any symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ a
$\mathcal {C}$ a ![]() $G$-symmetric monoidal structure on
$G$-symmetric monoidal structure on ![]() ${\text {Fun}}(BG, \mathcal {C})$. Moreover, if the tensor product in
${\text {Fun}}(BG, \mathcal {C})$. Moreover, if the tensor product in ![]() $\mathcal {C}$ is compatible with finite coproducts, this
$\mathcal {C}$ is compatible with finite coproducts, this ![]() $G$-symmetric monoidal structure will be compatible with additive transfers.
$G$-symmetric monoidal structure will be compatible with additive transfers.
Example 3.4.18 ( $G$-representations)
$G$-representations)
As a special case of the previous example, we can take ![]() $\mathcal {C}$ to be the category
$\mathcal {C}$ to be the category ![]() ${\text {Vect}}_{k}$ of
${\text {Vect}}_{k}$ of ![]() $k$-vector spaces with the tensor product as symmetric monoidal structure. We then obtain a functor
$k$-vector spaces with the tensor product as symmetric monoidal structure. We then obtain a functor
such that ![]() $\rho _{k}(G/H)$ is the category
$\rho _{k}(G/H)$ is the category ![]() ${\text {Rep}}_{H}(k) := {\text {Fun}}(BH, {\text {Vect}}_{k})$ of
${\text {Rep}}_{H}(k) := {\text {Fun}}(BH, {\text {Vect}}_{k})$ of ![]() $H$-representations and for subgroups
$H$-representations and for subgroups ![]() $H \subseteq K \subseteq G$:
$H \subseteq K \subseteq G$:
•
 $(q_{H}^{K})^{\circledast }$ is the restriction functor
$(q_{H}^{K})^{\circledast }$ is the restriction functor  ${\text {Res}}_{H}^{K} \colon {\text {Rep}}_{K}(k) \to {\text {Rep}}_{H}(k)$;
${\text {Res}}_{H}^{K} \colon {\text {Rep}}_{K}(k) \to {\text {Rep}}_{H}(k)$;•
 $(q_{H}^{K})_{\oplus }$ is the induced representation functor
$(q_{H}^{K})_{\oplus }$ is the induced representation functor  ${\text {Ind}}_{H}^{K} \colon {\text {Rep}}_{H}(k) \to {\text {Rep}}_{K}(k)$, left adjoint to
${\text {Ind}}_{H}^{K} \colon {\text {Rep}}_{H}(k) \to {\text {Rep}}_{K}(k)$, left adjoint to  ${\text {Res}}_{H}^{K}$, and given on objects by taking an
${\text {Res}}_{H}^{K}$, and given on objects by taking an  $H$-representation
$H$-representation  $V$ to
$V$ to  $\bigoplus _{K/H} V$ with induced action of
$\bigoplus _{K/H} V$ with induced action of  $K$;
$K$;•
 $(q_{H}^{K})_{\otimes }$ is the tensor-induction functor
$(q_{H}^{K})_{\otimes }$ is the tensor-induction functor  ${\text {Rep}}_{H}(k) \to {\text {Rep}}_{H}(k)$, given on objects by taking an
${\text {Rep}}_{H}(k) \to {\text {Rep}}_{H}(k)$, given on objects by taking an  $H$-representation
$H$-representation  $V$ to
$V$ to  $\bigotimes _{K/H} V$ with induced action of
$\bigotimes _{K/H} V$ with induced action of  $K$.
$K$.
As a more sophisticated version of this construction, we can instead consider the ![]() $\infty$-category
$\infty$-category ![]() $\mathrm {Perf}_{R}$ of perfect (i.e. dualizable) modules over an
$\mathrm {Perf}_{R}$ of perfect (i.e. dualizable) modules over an ![]() $\mathbb {E}_{\infty }$-ring spectrum
$\mathbb {E}_{\infty }$-ring spectrum ![]() $R$. Plugging this into the previous example we see that the
$R$. Plugging this into the previous example we see that the ![]() $\infty$-categories
$\infty$-categories ![]() ${\text {Rep}}^{\infty }_{H}(R):={\text {Fun}}(BH, \mathrm {Perf}_{R})$ fit together into a functor
${\text {Rep}}^{\infty }_{H}(R):={\text {Fun}}(BH, \mathrm {Perf}_{R})$ fit together into a functor
such that ![]() $\rho _R^{\infty }(G)(G/H) = {\text {Rep}}^{\infty }_{H}(R)$. This example will be important when we discuss Tambara functors arising from the algebraic
$\rho _R^{\infty }(G)(G/H) = {\text {Rep}}^{\infty }_{H}(R)$. This example will be important when we discuss Tambara functors arising from the algebraic ![]() $K$-theory of group actions in the next section.
$K$-theory of group actions in the next section.
Our final example of a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category compatible with additive transfers is the
$\infty$-category compatible with additive transfers is the ![]() $\infty$-category of genuine
$\infty$-category of genuine ![]() $G$-spectra. This is less formal than our previous examples, but the input we need is already in the literature.
$G$-spectra. This is less formal than our previous examples, but the input we need is already in the literature.
Proposition 3.4.19 The ![]() $\infty$-category
$\infty$-category ![]() ${\text {Sp}}^{G}$ of genuine
${\text {Sp}}^{G}$ of genuine ![]() $G$-spectra is a
$G$-spectra is a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category compatible with additive transfers.
$\infty$-category compatible with additive transfers.
Proof. Taking fixed point spectra for subgroups of ![]() $G$ gives a functor
$G$ gives a functor ![]() $\mathcal {O}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ that takes
$\mathcal {O}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ that takes ![]() $G/H$ to the
$G/H$ to the ![]() $\infty$-category
$\infty$-category ![]() ${\text {Sp}}^{H}$ of genuine
${\text {Sp}}^{H}$ of genuine ![]() $H$-spectra; this is the
$H$-spectra; this is the ![]() $G$-
$G$-![]() $\infty$-category of
$\infty$-category of ![]() $G$-spectra. The corresponding product-preserving functor
$G$-spectra. The corresponding product-preserving functor ![]() $\mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ extends to a functor
$\mathbb {F}_{G}^{{\text {op}}} \to {\text {Cat}}_\infty$ extends to a functor ![]() $\sigma _{G} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ such that for
$\sigma _{G} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ such that for ![]() $H \subseteq K \subseteq G$ the functor
$H \subseteq K \subseteq G$ the functor ![]() $(q_{H}^{K})_{\otimes } \colon {\text {Sp}}^{H} \to {\text {Sp}}^{K}$ is the multiplicative norm of [Reference Hill, Hopkins and RavenelHHR16]; this follows from the results of [Reference Bachmann and HoyoisBH21, § 9] by restricting the functor from spans of profinite groupoids defined there. For
$(q_{H}^{K})_{\otimes } \colon {\text {Sp}}^{H} \to {\text {Sp}}^{K}$ is the multiplicative norm of [Reference Hill, Hopkins and RavenelHHR16]; this follows from the results of [Reference Bachmann and HoyoisBH21, § 9] by restricting the functor from spans of profinite groupoids defined there. For ![]() $\phi \colon X \to Y$ in
$\phi \colon X \to Y$ in ![]() $\mathbb {F}_{G}$, the functor
$\mathbb {F}_{G}$, the functor ![]() $\phi ^{\circledast } \colon \sigma _{G}(Y) \to \sigma _{G}(X)$ has a left adjoint by [Reference Bachmann and HoyoisBH21, Lemma 9.7(2)]; for
$\phi ^{\circledast } \colon \sigma _{G}(Y) \to \sigma _{G}(X)$ has a left adjoint by [Reference Bachmann and HoyoisBH21, Lemma 9.7(2)]; for ![]() $H \subseteq K \subseteq G$ the left adjoint
$H \subseteq K \subseteq G$ the left adjoint ![]() $(q_{H}^{K})_{\oplus }$ is the classical (additive) transfer or induction functor. To see that the functor
$(q_{H}^{K})_{\oplus }$ is the classical (additive) transfer or induction functor. To see that the functor ![]() $\sigma _{G}$ is left adjointable we check the three remaining conditions in Proposition 3.4.7: conditions (1) and (3) hold since the
$\sigma _{G}$ is left adjointable we check the three remaining conditions in Proposition 3.4.7: conditions (1) and (3) hold since the ![]() $\infty$-categories of
$\infty$-categories of ![]() $G$-spectra are stable (hence, any right adjoint functor between them automatically preserves finite colimits). To check condition (4) we use that any
$G$-spectra are stable (hence, any right adjoint functor between them automatically preserves finite colimits). To check condition (4) we use that any ![]() $H$-spectrum is a sifted colimit of desuspensions of suspension spectra
$H$-spectrum is a sifted colimit of desuspensions of suspension spectra ![]() $\Sigma ^{\infty }_{+}X$ with
$\Sigma ^{\infty }_{+}X$ with ![]() $X$ a finite
$X$ a finite ![]() $H$-set, and the functors involved preserve (sifted) colimits and desuspensions. Hence, it suffices to check that the canonical map
$H$-set, and the functors involved preserve (sifted) colimits and desuspensions. Hence, it suffices to check that the canonical map
is an equivalence for ![]() $X \in \mathbb {F}_{H}$. But here all the functors are given on suspension spectra of finite
$X \in \mathbb {F}_{H}$. But here all the functors are given on suspension spectra of finite ![]() $H$-sets by the suspension spectra on the corresponding functors for finite
$H$-sets by the suspension spectra on the corresponding functors for finite ![]() $H$-sets, so this follows from Example 3.4.15. The same argument works for distributivity, since we also have
$H$-sets, so this follows from Example 3.4.15. The same argument works for distributivity, since we also have ![]() $f_{\otimes }\Sigma ^{\infty }_{+}X \simeq \Sigma ^{\infty }_{+}f_{*}X$.
$f_{\otimes }\Sigma ^{\infty }_{+}X \simeq \Sigma ^{\infty }_{+}f_{*}X$.
Remark 3.4.20 The adjointability condition here reduces by Remark 3.4.8 to a double coset formula for additive transfers. This is a basic fact in equivariant stable homotopy theory that has surely long been well-known to the experts, but the only explicit references we could find are [Reference Hill, Hopkins and RavenelHHR16, Proposition A.30] (applied to the direct sum in orthogonal spectra) and [Reference PatchkoriaPat16, Corollary 5.2]. The distributivity condition also appears (in terms of orthogonal spectra) as [Reference Hill, Hopkins and RavenelHHR16, Proposition A.37].
Variant 3.4.21 Following Blumberg and Hill [Reference Blumberg and HillBH18] we can consider subcategories ![]() $\mathbb {F}_{G,\mathcal {I}}$ where
$\mathbb {F}_{G,\mathcal {I}}$ where ![]() $\mathcal {I}$ is an indexing system as in [Reference Blumberg and HillBH18, Definition 1.2]; by [Reference Blumberg and HillBH18, Theorem 1.4] these are precisely the subcategories of
$\mathcal {I}$ is an indexing system as in [Reference Blumberg and HillBH18, Definition 1.2]; by [Reference Blumberg and HillBH18, Theorem 1.4] these are precisely the subcategories of ![]() $\mathbb {F}_{G}$ such that
$\mathbb {F}_{G}$ such that ![]() $(\mathbb {F}_{G},\mathbb {F}_{G,\mathcal {I}})$ is a span pair. Since
$(\mathbb {F}_{G},\mathbb {F}_{G,\mathcal {I}})$ is a span pair. Since ![]() $\mathbb {F}_{G}$ is locally cartesian closed, we then have a bispan triple
$\mathbb {F}_{G}$ is locally cartesian closed, we then have a bispan triple ![]() $(\mathbb {F}_{G}, \mathbb {F}_{G,\mathcal {I}}, \mathbb {F}_{G})$. Product-preserving functors out of
$(\mathbb {F}_{G}, \mathbb {F}_{G,\mathcal {I}}, \mathbb {F}_{G})$. Product-preserving functors out of ![]() $\operatorname {Span}_{\mathcal {I}}(\mathbb {F}_{G})$ are
$\operatorname {Span}_{\mathcal {I}}(\mathbb {F}_{G})$ are ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories where only some subclass of multiplicative norms exist, and we can characterize distributivity for such functors by the analogue of Proposition 3.4.11 with the map
$\infty$-categories where only some subclass of multiplicative norms exist, and we can characterize distributivity for such functors by the analogue of Proposition 3.4.11 with the map ![]() $\psi$ restricted to lie in
$\psi$ restricted to lie in ![]() $\mathbb {F}_{G,\mathcal {I}}$.
$\mathbb {F}_{G,\mathcal {I}}$.
Variant 3.4.22 We can also consider a ![]() $G$-equivariant analogue of § 3.2: using [Reference Bachmann and HoyoisBH21, Proposition C.18] a
$G$-equivariant analogue of § 3.2: using [Reference Bachmann and HoyoisBH21, Proposition C.18] a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category determines by right Kan extension a functor
$\infty$-category determines by right Kan extension a functor ![]() $\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}_{G}) \to {\text {Cat}}_\infty$, where
$\operatorname {Span}_{\mathrm {fin}}(\mathcal {S}_{G}) \to {\text {Cat}}_\infty$, where ![]() $\mathcal {S}_{G,\mathrm {fin}}$ denotes the subcategory of
$\mathcal {S}_{G,\mathrm {fin}}$ denotes the subcategory of ![]() $\mathcal {S}_{G}$ containing the maps
$\mathcal {S}_{G}$ containing the maps ![]() $\phi \colon X \to Y$ such that for every map
$\phi \colon X \to Y$ such that for every map ![]() $G/H \to Y$, the pullback
$G/H \to Y$, the pullback ![]() $X \times _{Y} G/H$ is a finite
$X \times _{Y} G/H$ is a finite ![]() $G$-set. Here
$G$-set. Here ![]() $(\mathcal {S}_{G}, \mathcal {S}_{G,\mathrm {fin}}, \mathcal {S}_{G})$ is a bispan triple, and we might say that the
$(\mathcal {S}_{G}, \mathcal {S}_{G,\mathrm {fin}}, \mathcal {S}_{G})$ is a bispan triple, and we might say that the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category is ‘compatible with
$\infty$-category is ‘compatible with ![]() $G$-space-indexed
$G$-space-indexed ![]() $G$-colimits’ if this is distributive. We expect that this should hold for the
$G$-colimits’ if this is distributive. We expect that this should hold for the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category of genuine
$\infty$-category of genuine ![]() $G$-spectra and, by analogy with [Reference Gepner, Haugseng and KockGHK22], that monads in the
$G$-spectra and, by analogy with [Reference Gepner, Haugseng and KockGHK22], that monads in the ![]() $(\infty,2)$-category
$(\infty,2)$-category ![]() ${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S}_{G})$ should be related to a notion of
${\text {BISPAN}}_{\mathrm {fin}}(\mathcal {S}_{G})$ should be related to a notion of ![]() $G$-
$G$- ![]() $\infty$-operads (see [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16]).
$\infty$-operads (see [Reference Barwick, Dotto, Glasman, Nardin and ShahBDG+16]).
Variant 3.4.23 In [Reference Bachmann and HoyoisBH21, Chapter 9], Bachmann and Hoyois define ![]() $\infty$-categories of equivariant spectra for profinite groupoids, and we can also consider distributivity in this setting. We can take the
$\infty$-categories of equivariant spectra for profinite groupoids, and we can also consider distributivity in this setting. We can take the ![]() $(2,1)$-category of finite groupoids
$(2,1)$-category of finite groupoids ![]() $\mathrm {FinGpd} \subset \mathcal {S}$ to be the full subcategory of spaces spanned by
$\mathrm {FinGpd} \subset \mathcal {S}$ to be the full subcategory of spaces spanned by ![]() $1$-truncated spaces with finite
$1$-truncated spaces with finite ![]() $\pi _0, \pi _1$. We then form the
$\pi _0, \pi _1$. We then form the ![]() $(2,1)$-category of profinite groupoids by taking pro-objects:
$(2,1)$-category of profinite groupoids by taking pro-objects: ![]() $\mathrm {ProfGpd}:=\mathrm {Pro}(\mathrm {FinGpd})$. Let
$\mathrm {ProfGpd}:=\mathrm {Pro}(\mathrm {FinGpd})$. Let ![]() $\mathrm {ProfGpd}_{{\text {fp}}}$ be the subcategory containing only the finitely presented maps as in [Reference Bachmann and HoyoisBH21, § 9.1]. It then follows from [Reference Bachmann and HoyoisBH21, Lemmas 9.3 and 9.5] and Lemma 2.4.6 that we have a bispan triple
$\mathrm {ProfGpd}_{{\text {fp}}}$ be the subcategory containing only the finitely presented maps as in [Reference Bachmann and HoyoisBH21, § 9.1]. It then follows from [Reference Bachmann and HoyoisBH21, Lemmas 9.3 and 9.5] and Lemma 2.4.6 that we have a bispan triple
In [Reference Bachmann and HoyoisBH21, Chapter 9] equivariant spectra are defined as a functor
we expect that this is distributive, giving a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
3.5 Motivic bispans and normed  $\infty$-categories
$\infty$-categories
In this section we will relate the normed ![]() $\infty$-categories of Bachmann–Hoyois to functors from certain bispans in schemes (and, more generally, algebraic spaces) to
$\infty$-categories of Bachmann–Hoyois to functors from certain bispans in schemes (and, more generally, algebraic spaces) to ![]() ${\text {CAT}}_{\infty }$. As an example of this, we will see that the results of [Reference Bachmann and HoyoisBH21] imply that
${\text {CAT}}_{\infty }$. As an example of this, we will see that the results of [Reference Bachmann and HoyoisBH21] imply that ![]() $\infty$-categories of motivic spectra give such a functor. We begin by describing some bispan triples on schemes.
$\infty$-categories of motivic spectra give such a functor. We begin by describing some bispan triples on schemes.
Warning 3.5.1 Throughout this section, schemes and algebraic spaces are always assumed to be quasi-compact and quasi-separated (qcqs).Footnote 13
Notation 3.5.2 If ![]() $S$ is a (qcqs) scheme, we write
$S$ is a (qcqs) scheme, we write ![]() $\mathrm {Sch}_{S}$ for the category of (qcqs) schemes over
$\mathrm {Sch}_{S}$ for the category of (qcqs) schemes over ![]() $S$. (This has pullbacks since qcqs morphisms are closed under base change, see [Sta, Tags 01KU and 01K5].)
$S$. (This has pullbacks since qcqs morphisms are closed under base change, see [Sta, Tags 01KU and 01K5].)
Proposition 3.5.3 The following are bispan triples:
(i)
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}}, \mathrm {Sch}_{S}^{{\text {qp}}})$ for any scheme
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}}, \mathrm {Sch}_{S}^{{\text {qp}}})$ for any scheme  $S$, where
$S$, where  $\mathrm {Sch}_{S}^{{\text {flf}}}$ consists of finite locally free (meaning finite, flat, and of finite presentation) morphisms of
$\mathrm {Sch}_{S}^{{\text {flf}}}$ consists of finite locally free (meaning finite, flat, and of finite presentation) morphisms of  $S$-schemes and
$S$-schemes and  $\mathrm {Sch}_{S}^{{\text {qp}}}$ of quasiprojective morphisms of
$\mathrm {Sch}_{S}^{{\text {qp}}}$ of quasiprojective morphisms of  $S$-schemes;
$S$-schemes;(ii)
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{{\text {qp}}})$ for any scheme
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{{\text {qp}}})$ for any scheme  $S$, where
$S$, where  $\mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ consists of finite étale morphisms of
$\mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ consists of finite étale morphisms of  $S$-schemes;
$S$-schemes;(iii)
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}}, \mathrm {Sch}_{S}^{\mathrm {smqp}})$ for any scheme
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}}, \mathrm {Sch}_{S}^{\mathrm {smqp}})$ for any scheme  $S$, where
$S$, where  $\mathrm {Sch}_{S}^{\mathrm {smqp}}$ consists of smooth and quasiprojective morphisms of
$\mathrm {Sch}_{S}^{\mathrm {smqp}}$ consists of smooth and quasiprojective morphisms of  $S$-schemes;
$S$-schemes;(iv)
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{\mathrm {smqp}})$ for any scheme
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{\mathrm {smqp}})$ for any scheme  $S$;
$S$;(v)
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{\mathrm {proj}})$ for any scheme
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {Sch}_{S}^{\mathrm {proj}})$ for any scheme  $S$, where
$S$, where  $\mathrm {Sch}_{S}^{\mathrm {proj}}$ consists of projective morphisms of
$\mathrm {Sch}_{S}^{\mathrm {proj}}$ consists of projective morphisms of  $S$-schemes.
$S$-schemes.
Proof. The classes of morphisms of schemes that are finite locally free, quasiprojective, smooth, finite, and étale are all closed under base change by [Sta, Tags 02KD,0B3G,01VB,01WL,02GO], respectively. Hence, the subcategories ![]() $\mathrm {Sch}_{S}^{{\text {flf}}}$,
$\mathrm {Sch}_{S}^{{\text {flf}}}$, ![]() $\mathrm {Sch}_{S}^{{\text {qp}}}$,
$\mathrm {Sch}_{S}^{{\text {qp}}}$, ![]() $\mathrm {Sch}_{S}^{\mathrm {smqp}}$, and
$\mathrm {Sch}_{S}^{\mathrm {smqp}}$, and ![]() $\mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ of
$\mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ of ![]() $\mathrm {Sch}_{S}$ all give span pairs.
$\mathrm {Sch}_{S}$ all give span pairs.
Now the main point is the existence of Weil restrictions for schemes: if ![]() $f \colon S' \to S$ is a morphism of schemes and
$f \colon S' \to S$ is a morphism of schemes and ![]() $X$ is an
$X$ is an ![]() $S'$-scheme, the Weil restriction
$S'$-scheme, the Weil restriction ![]() $R_{f}X$, if it exists, is an
$R_{f}X$, if it exists, is an ![]() $S$-scheme that represents the functor
$S$-scheme that represents the functor
note that this is exactly the requirement (21) for a distributivity diagram for ![]() $X \to S'$ and
$X \to S'$ and ![]() $f$.
$f$.
By [Reference Bosch, Lütkebohmert and RaynaudBLR17, Theorem 7.6.4], the Weil restriction ![]() $R_{f}X$ exists if
$R_{f}X$ exists if ![]() $f$ is a finite locally free morphism and
$f$ is a finite locally free morphism and ![]() $X$ is quasiprojective. Moreover,
$X$ is quasiprojective. Moreover, ![]() $R_{f}X$ is quasiprojective over
$R_{f}X$ is quasiprojective over ![]() $S$ by [Reference Bachmann and HoyoisBH21, Lemma 2.13]. This gives the bispan triple (i), from which bispan triple (ii) is trivially obtained by restricting from finite locally free morphisms to the subclass of finite étale ones. For bispan triples (iii) and (iv) the only additional input needed is that
$S$ by [Reference Bachmann and HoyoisBH21, Lemma 2.13]. This gives the bispan triple (i), from which bispan triple (ii) is trivially obtained by restricting from finite locally free morphisms to the subclass of finite étale ones. For bispan triples (iii) and (iv) the only additional input needed is that ![]() $R_{f}$ takes smooth morphisms to smooth morphisms, which holds by [Reference Bosch, Lütkebohmert and RaynaudBLR17, Proposition 7.6.5(h)], while for bispan triple (v) we use that
$R_{f}$ takes smooth morphisms to smooth morphisms, which holds by [Reference Bosch, Lütkebohmert and RaynaudBLR17, Proposition 7.6.5(h)], while for bispan triple (v) we use that ![]() $R_{f}$ preserves proper morphisms if
$R_{f}$ preserves proper morphisms if ![]() $f$ is finite étale by [Reference Bosch, Lütkebohmert and RaynaudBLR17, Proposition 7.6.5(f)] and that a morphism is projective if and only if it is proper and quasiprojective by [Sta, Tag 0BCL].
$f$ is finite étale by [Reference Bosch, Lütkebohmert and RaynaudBLR17, Proposition 7.6.5(f)] and that a morphism is projective if and only if it is proper and quasiprojective by [Sta, Tag 0BCL].
We now review the construction of a distributive functor for the bispan triple (iv) from motivic spectra, due to Bachmann and Hoyois.
Notation 3.5.4 We write ![]() $\mathrm {SH}(S)$ for the
$\mathrm {SH}(S)$ for the ![]() $\infty$-category of motivic spectra over a base scheme
$\infty$-category of motivic spectra over a base scheme ![]() $S$ and
$S$ and ![]() $\mathrm {H}(S)$ for that of motivic spaces over
$\mathrm {H}(S)$ for that of motivic spaces over ![]() $S$. For any morphism of schemes
$S$. For any morphism of schemes ![]() $f \colon S \to S'$ we have a pullback functor
$f \colon S \to S'$ we have a pullback functor ![]() $f^{*} \colon \mathrm {SH}(S') \to \mathrm {SH}(S)$, and similarly in the unstable case. This gives functors
$f^{*} \colon \mathrm {SH}(S') \to \mathrm {SH}(S)$, and similarly in the unstable case. This gives functors ![]() $\mathrm {SH},\mathrm {H} \colon \mathrm {Sch}^{{\text {op}}} \to {\text {Cat}}_\infty$.
$\mathrm {SH},\mathrm {H} \colon \mathrm {Sch}^{{\text {op}}} \to {\text {Cat}}_\infty$.
In [Reference Bachmann and HoyoisBH21], Bachmann and Hoyois promoted the contravariant functor ![]() $X \mapsto \mathrm {SH}(X)$ to include a multiplicative pushforward for finite étale morphisms, encoded as a functor out of a span category
$X \mapsto \mathrm {SH}(X)$ to include a multiplicative pushforward for finite étale morphisms, encoded as a functor out of a span category
Given a finite étale morphism ![]() $g\colon X \rightarrow Y$, the functor
$g\colon X \rightarrow Y$, the functor
is first constructed unstably as a functor on the level of the pointed unstable motivic homotopy ![]() $\infty$-category,
$\infty$-category,
This functor is, in turn, induced by the functor of Weil restriction [Reference Bosch, Lütkebohmert and RaynaudBLR17, § 7.6], ![]() $R_g\colon \mathrm {SmQP}_X \rightarrow \mathrm {SmQP}_Y$, where
$R_g\colon \mathrm {SmQP}_X \rightarrow \mathrm {SmQP}_Y$, where ![]() $\mathrm {SmQP}_X$ denotes the full subcategory of
$\mathrm {SmQP}_X$ denotes the full subcategory of ![]() $\mathrm {Sch}_{X}$ spanned by smooth and quasiprojective
$\mathrm {Sch}_{X}$ spanned by smooth and quasiprojective ![]() $X$-schemes, using the fact that the inclusion
$X$-schemes, using the fact that the inclusion ![]() $\mathrm {SmQP}_X \subset \mathrm {Sm}_X$ into the full subcategory of smooth
$\mathrm {SmQP}_X \subset \mathrm {Sm}_X$ into the full subcategory of smooth ![]() $X$-schemes induces equivalent motivic unstable categories (since every smooth
$X$-schemes induces equivalent motivic unstable categories (since every smooth ![]() $X$-scheme is Zariski-locally also quasiprojective). We refer to [Reference Bachmann and HoyoisBH21, § 1.6] for a summary of the construction and [Reference Bachmann and HoyoisBH21, § 6.1] for a detailed construction of (40).
$X$-scheme is Zariski-locally also quasiprojective). We refer to [Reference Bachmann and HoyoisBH21, § 1.6] for a summary of the construction and [Reference Bachmann and HoyoisBH21, § 6.1] for a detailed construction of (40).
Given a smooth morphism ![]() $f\colon X \rightarrow Y$ of schemes, the pullback functor
$f\colon X \rightarrow Y$ of schemes, the pullback functor ![]() $f^*$ admits a left adjoint
$f^*$ admits a left adjoint
This left adjoint should be thought of as an additive pushforward along ![]() $f$; indeed, if
$f$; indeed, if ![]() $I$ is a finite set and
$I$ is a finite set and ![]() $\nabla _I \colon \coprod _I X \rightarrow X$ is the fold map, then, under the identification
$\nabla _I \colon \coprod _I X \rightarrow X$ is the fold map, then, under the identification ![]() $\mathrm {SH}(\coprod _I X) \simeq \mathrm {SH}(X)^{\times I}$, the functor
$\mathrm {SH}(\coprod _I X) \simeq \mathrm {SH}(X)^{\times I}$, the functor ![]() $(\nabla _I)_{\sharp }$ is given by
$(\nabla _I)_{\sharp }$ is given by
The functor ![]() $f_{\sharp }$ is first constructed unstably as a functor
$f_{\sharp }$ is first constructed unstably as a functor
which, in turn, is induced by the functor ![]() $\mathrm {Sm}_X \rightarrow \mathrm {Sm}_Y$ given by composition with
$\mathrm {Sm}_X \rightarrow \mathrm {Sm}_Y$ given by composition with ![]() $f$ (i.e. the functor that sends a smooth
$f$ (i.e. the functor that sends a smooth ![]() $X$-scheme
$X$-scheme ![]() $T$ to itself regarded as a
$T$ to itself regarded as a ![]() $Y$-scheme); see [Reference HoyoisHoy17, § 4.1, Lemma 6.2] for a construction in the language of this paper in the more general context of equivariant motivic homotopy theory.
$Y$-scheme); see [Reference HoyoisHoy17, § 4.1, Lemma 6.2] for a construction in the language of this paper in the more general context of equivariant motivic homotopy theory.
The importance of this additional left adjoint functoriality in formulating smooth base change was first pointed out by Voevodsky [Reference VoevodskyVoe99] and worked out by Ayoub in [Reference AyoubAyo07]; see [Reference HoyoisHoy17, § 6.1, Proposition 4.2] for an ![]() $\infty$-categorical formulation (in the more general equivariant context). In our language, smooth base change for motivic spectra says that the functor
$\infty$-categorical formulation (in the more general equivariant context). In our language, smooth base change for motivic spectra says that the functor ![]() $\mathrm {SH} \colon \mathrm {Sch}^{{\text {op}}} \to {\text {Cat}}_\infty$ is left adjointable with respect to smooth maps. Moreover, combining this with [Reference Bachmann and HoyoisBH21, Proposition 5.10(1)] we get that the functor (40) is
$\mathrm {SH} \colon \mathrm {Sch}^{{\text {op}}} \to {\text {Cat}}_\infty$ is left adjointable with respect to smooth maps. Moreover, combining this with [Reference Bachmann and HoyoisBH21, Proposition 5.10(1)] we get that the functor (40) is ![]() $\mathrm {smqp}$-distributive. Applying Theorem 2.5.1, these results imply the following.
$\mathrm {smqp}$-distributive. Applying Theorem 2.5.1, these results imply the following.
Theorem 3.5.5 Motivic spectra give a ![]() $\mathrm {smqp}$-distributive functor
$\mathrm {smqp}$-distributive functor
and so a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
As indicated already in [Reference Bachmann and HoyoisBH21, Remark 2.14], the restriction to those smooth morphisms that are quasiprojective here is an artifact of the restriction of ![]() $\mathrm {SH}$ to schemes instead of algebraic spaces. We will therefore extend this result by working with algebraic spaces.
$\mathrm {SH}$ to schemes instead of algebraic spaces. We will therefore extend this result by working with algebraic spaces.
Notation 3.5.6 For a (qcqs) scheme ![]() $S$, we write
$S$, we write ![]() $\mathrm {AlgSpc}_S$ for the category of (qcqs) algebraic spaces over
$\mathrm {AlgSpc}_S$ for the category of (qcqs) algebraic spaces over ![]() $S$.Footnote 14 This category has pullbacks since qcqs morphisms of algebraic spaces are closed under base change by [Sta, Tags 03KL,03HF]; note also that for an
$S$.Footnote 14 This category has pullbacks since qcqs morphisms of algebraic spaces are closed under base change by [Sta, Tags 03KL,03HF]; note also that for an ![]() $S$-scheme
$S$-scheme ![]() $S'$ we have an equivalence
$S'$ we have an equivalence
by [Sta, Tag 04SG].
Here we again have several bispan triples.
Proposition 3.5.7 The following are bispan triples:
(i)
 $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}}, \mathrm {AlgSpc}_{S})$ for any scheme
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}}, \mathrm {AlgSpc}_{S})$ for any scheme  $S$, where
$S$, where  $\mathrm {AlgSpc}_{S}^{{\text {flf}}}$ consists of finite locally free morphisms of algebraic spaces over
$\mathrm {AlgSpc}_{S}^{{\text {flf}}}$ consists of finite locally free morphisms of algebraic spaces over  $S$;
$S$;(ii)
 $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}_{S})$ for any scheme
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}_{S})$ for any scheme  $S$, where
$S$, where  $\mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ consists of finite étale morphisms of algebraic spaces over
$\mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$ consists of finite étale morphisms of algebraic spaces over  $S$;
$S$;(iii)
 $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}}, \mathrm {AlgSpc}^{\mathrm {sm}}_{S})$ for any scheme
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}}, \mathrm {AlgSpc}^{\mathrm {sm}}_{S})$ for any scheme  $S$, where
$S$, where  $\mathrm {AlgSpc}_{S}^{\mathrm {sm}}$ consists of smooth morphisms of algebraic spaces over
$\mathrm {AlgSpc}_{S}^{\mathrm {sm}}$ consists of smooth morphisms of algebraic spaces over  $S$;
$S$;(iv)
 $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}^{\mathrm {sm}}_{S})$ for any scheme
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}^{\mathrm {sm}}_{S})$ for any scheme  $S$;
$S$;(v)
 $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}^{\mathrm {prop}}_{S})$ for any scheme
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}, \mathrm {AlgSpc}^{\mathrm {prop}}_{S})$ for any scheme  $S$, where
$S$, where  $\mathrm {AlgSpc}^{\mathrm {prop}}_{S}$ consists of proper morphisms of algebraic spaces over
$\mathrm {AlgSpc}^{\mathrm {prop}}_{S}$ consists of proper morphisms of algebraic spaces over  $S$.
$S$.
Proof. Morphisms of algebraic spaces that are finite locally free, finite, étale, and smooth are closed under base change by [Sta, Tags 03ZY, 03ZS, 0466, 03ZE], respectively. Thus, the subcategories ![]() $\mathrm {AlgSpc}_{S}^{{\text {flf}}}$,
$\mathrm {AlgSpc}_{S}^{{\text {flf}}}$, ![]() $\mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$,
$\mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}}$, ![]() $\mathrm {AlgSpc}_{S}^{\mathrm {sm}}$ of
$\mathrm {AlgSpc}_{S}^{\mathrm {sm}}$ of ![]() $\mathrm {AlgSpc}_{S}$ all give span pairs.
$\mathrm {AlgSpc}_{S}$ all give span pairs.
Suppose ![]() $f \colon Y \to Z$ is a finite locally free morphism of algebraic spaces. Then the functor
$f \colon Y \to Z$ is a finite locally free morphism of algebraic spaces. Then the functor
admits a right adjoint ![]() $R_{f}$, given by Weil restriction of algebraic spaces, by a result of Rydh [Reference RydhRyd11, Theorem 3.7]; note that
$R_{f}$, given by Weil restriction of algebraic spaces, by a result of Rydh [Reference RydhRyd11, Theorem 3.7]; note that ![]() $R_{f}$ preserves the qcqs property we require by [Reference RydhRyd11, Proposition 3.8(xiii,xix)]. This gives the bispan triples (i) and (ii) (since finite étale morphisms are in particular finite locally free).
$R_{f}$ preserves the qcqs property we require by [Reference RydhRyd11, Proposition 3.8(xiii,xix)]. This gives the bispan triples (i) and (ii) (since finite étale morphisms are in particular finite locally free).
To obtain bispan triples (iii) and (iv) it suffices to note that ![]() $R_f$ converts smooth morphisms to smooth morphisms. If
$R_f$ converts smooth morphisms to smooth morphisms. If ![]() $f \colon X \to Y$ is a finite locally free morphism of schemes this follows from [Reference RydhRyd11, Proposition 3.5(i,iv)] and [Sta, Tag 0DP0]. The extension to the general case is easy: first note that for
$f \colon X \to Y$ is a finite locally free morphism of schemes this follows from [Reference RydhRyd11, Proposition 3.5(i,iv)] and [Sta, Tag 0DP0]. The extension to the general case is easy: first note that for ![]() $W$ over
$W$ over ![]() $X$ we have that
$X$ we have that ![]() $R_{f}W \to Y$ is smooth if and only if its pullback along any morphism
$R_{f}W \to Y$ is smooth if and only if its pullback along any morphism ![]() $g \colon T \to Y$ with
$g \colon T \to Y$ with ![]() $T$ a scheme is smooth, by [Sta, Tag 03ZF]. In the pullback square
$T$ a scheme is smooth, by [Sta, Tag 03ZF]. In the pullback square

the algebraic space ![]() $U$ is a scheme since
$U$ is a scheme since ![]() $f$ is finite and so, by definition, representable. We also have the base change equivalence
$f$ is finite and so, by definition, representable. We also have the base change equivalence ![]() $g^{*}R_{f}W \cong R_{f'}g'^{*}W$, and if
$g^{*}R_{f}W \cong R_{f'}g'^{*}W$, and if ![]() $W$ is smooth over
$W$ is smooth over ![]() $X$, then
$X$, then ![]() $R_{f'}g'^{*}W$ is smooth over
$R_{f'}g'^{*}W$ is smooth over ![]() $T$ since the base change
$T$ since the base change ![]() $g'^{*}W$ is smooth over
$g'^{*}W$ is smooth over ![]() $U$ and
$U$ and ![]() $f'$ is a finite locally free morphism of schemes. Finally, bispan triple (v) holds since by the same argument starting with [Reference RydhRyd11, Remark 3.9]
$f'$ is a finite locally free morphism of schemes. Finally, bispan triple (v) holds since by the same argument starting with [Reference RydhRyd11, Remark 3.9] ![]() $R_{f}$ preserves proper morphisms if
$R_{f}$ preserves proper morphisms if ![]() $f$ is finite étale.
$f$ is finite étale.
In order to work with motivic spectra over algebraic spaces effectively we record the following lemma which amounts to saying that any Nisnevich sheaf on algebraic spaces is right Kan extended from schemes.
Lemma 3.5.8 Let ![]() $\mathcal {C}$ be a complete
$\mathcal {C}$ be a complete ![]() $\infty$-category and
$\infty$-category and ![]() $S$ a scheme, and let
$S$ a scheme, and let
be the inclusion. Then the restriction functor ![]() $\iota ^*\colon \mathrm {PShv}( \mathrm {AlgSpc}_S, \mathcal {C}) \rightarrow \mathrm {PShv}( \mathrm {Sch}_S, \mathcal {C})$ induces an equivalence of
$\iota ^*\colon \mathrm {PShv}( \mathrm {AlgSpc}_S, \mathcal {C}) \rightarrow \mathrm {PShv}( \mathrm {Sch}_S, \mathcal {C})$ induces an equivalence of ![]() $\infty$-categories:
$\infty$-categories:
with the inverse given by right Kan extension.
Proof. Let
denote the right adjoint to ![]() $\iota ^*$ which is computed by right Kan extension. We first claim that
$\iota ^*$ which is computed by right Kan extension. We first claim that ![]() $\iota _*$ preserves Nisnevich sheaves, i.e. there exists a filler in the following diagram.
$\iota _*$ preserves Nisnevich sheaves, i.e. there exists a filler in the following diagram.

According to [Reference Gepner and HellerGH23, Lemma 2.23], it suffices to verify that the functor ![]() $\iota$ is topologically cocontinuousFootnote 15 for the Nisnevich topology on
$\iota$ is topologically cocontinuousFootnote 15 for the Nisnevich topology on ![]() $\mathrm {Sch}_S$ and on
$\mathrm {Sch}_S$ and on ![]() $\mathrm {AlgSpc}_S$, as this implies that
$\mathrm {AlgSpc}_S$, as this implies that ![]() $\iota ^*$ preserves
$\iota ^*$ preserves ![]() $\mathrm {Nis}$-local equivalences and, thus,
$\mathrm {Nis}$-local equivalences and, thus, ![]() $\iota _*$ preserves sheaves.
$\iota _*$ preserves sheaves.
Unwinding definitions, this means we need to prove the following claim.
(*) For any
 $X \in \mathrm {Sch}_S$ and any Nisnevich sieve
$X \in \mathrm {Sch}_S$ and any Nisnevich sieve  $R' \hookrightarrow \iota (X)$ of algebraic spaces, the sieve on
$R' \hookrightarrow \iota (X)$ of algebraic spaces, the sieve on  $\mathrm {Sch}_S$ generated by morphisms of schemes
$\mathrm {Sch}_S$ generated by morphisms of schemes  $X' \rightarrow X$ such that
$X' \rightarrow X$ such that  $\iota (X') \rightarrow \iota (X)$ factors through
$\iota (X') \rightarrow \iota (X)$ factors through  $R'$ is a Nisnevich sieve of
$R'$ is a Nisnevich sieve of  $X$.
$X$.
This condition is verified by [Reference KnutsonKnu71, Chapter II, Theorem 6.4]; indeed for ![]() $x \in X$ and
$x \in X$ and ![]() $f\colon Y \rightarrow X$ an étale morphism such that we have a lift
$f\colon Y \rightarrow X$ an étale morphism such that we have a lift

this result tells us that we can find a completely decomposed étale morphism ![]() $U \rightarrow Y$ with
$U \rightarrow Y$ with ![]() $U$ an affine scheme such that
$U$ an affine scheme such that ![]() $\operatorname {Spec} \kappa (x) \rightarrow Y$ factors through
$\operatorname {Spec} \kappa (x) \rightarrow Y$ factors through ![]() $U$. Since the composite
$U$. Since the composite ![]() $U \rightarrow X$ is an étale morphism, the desired claim is verified.
$U \rightarrow X$ is an étale morphism, the desired claim is verified.
Now we claim that ![]() $\iota ^*$ also preserves sheaves. Indeed, if
$\iota ^*$ also preserves sheaves. Indeed, if ![]() $\{ U_{\alpha } \rightarrow X \}$ is a family which generates a Nisnevich covering family of schemes, then it is still a Nisnevich covering family of algebraic spaces. Therefore
$\{ U_{\alpha } \rightarrow X \}$ is a family which generates a Nisnevich covering family of schemes, then it is still a Nisnevich covering family of algebraic spaces. Therefore ![]() $\iota$ is also a morphism of sites,Footnote 16 and, thus,
$\iota$ is also a morphism of sites,Footnote 16 and, thus, ![]() $\iota ^*$ preserves sheaves, i.e. there exists a filler in the following diagram:
$\iota ^*$ preserves sheaves, i.e. there exists a filler in the following diagram:

Therefore, we have an adjunction on the level of Nisnevich sheaves
where ![]() $\iota _{*}$ is fully faithful since it is given by right Kan extension along the fully faithful functor
$\iota _{*}$ is fully faithful since it is given by right Kan extension along the fully faithful functor ![]() $\iota$. Equivalently, the counit transformation
$\iota$. Equivalently, the counit transformation ![]() $\iota ^{*}\iota _{*} \to {\text {id}}$ is an equivalence.
$\iota ^{*}\iota _{*} \to {\text {id}}$ is an equivalence.
It then suffices to prove that the unit transformation ![]() ${\text {id}} \to \iota _{*}\iota ^{*}$ is also an equivalence. According to [Reference LurieLur18, Theorem 3.4.2.1], any qcqs algebraic space admits a scalloped decomposition in the sense of [Reference LurieLur18, Definition 2.5.3.1]. In this context, this means that any
${\text {id}} \to \iota _{*}\iota ^{*}$ is also an equivalence. According to [Reference LurieLur18, Theorem 3.4.2.1], any qcqs algebraic space admits a scalloped decomposition in the sense of [Reference LurieLur18, Definition 2.5.3.1]. In this context, this means that any ![]() $X \in \mathrm {AlgSpc}_S$ admits a sequence of open immersions
$X \in \mathrm {AlgSpc}_S$ admits a sequence of open immersions
such that for any ![]() $1 \leq i \leq n$ we have a bicartesian diagram in algebraic spaces
$1 \leq i \leq n$ we have a bicartesian diagram in algebraic spaces

where each ![]() $p_i$ is étale. A result of Morel and Voevodsky [Reference Morel and VoevodskyMV99] (in the form [Reference LurieLur18, Theorem 3.7.5.1]) states that any Nisnevich sheaf converts the above square to a cartesian square. Now although
$p_i$ is étale. A result of Morel and Voevodsky [Reference Morel and VoevodskyMV99] (in the form [Reference LurieLur18, Theorem 3.7.5.1]) states that any Nisnevich sheaf converts the above square to a cartesian square. Now although ![]() $W_i$ is not necessarily a scheme, it is an open sub-algebraic space of an affine scheme and, hence, is separated. Therefore, by induction and the fact that
$W_i$ is not necessarily a scheme, it is an open sub-algebraic space of an affine scheme and, hence, is separated. Therefore, by induction and the fact that ![]() $\iota ^*$ is computed on the level of presheaves, the map
$\iota ^*$ is computed on the level of presheaves, the map ![]() $F \rightarrow \iota _*\iota ^*F$ is an equivalence for any Nisnevich sheaf
$F \rightarrow \iota _*\iota ^*F$ is an equivalence for any Nisnevich sheaf ![]() $F$ as soon as we know that it is an equivalence when evaluated on a separated algebraic space.
$F$ as soon as we know that it is an equivalence when evaluated on a separated algebraic space.
Now, if ![]() $X$ is a separated algebraic space then, in the scalloped decomposition of
$X$ is a separated algebraic space then, in the scalloped decomposition of ![]() $X$, we see that
$X$, we see that ![]() $W_i$ is, in fact, affine, as argued in the proof of [Reference KhanKha19, Proposition 2.2.13]. Therefore, by induction again, we need only check that
$W_i$ is, in fact, affine, as argued in the proof of [Reference KhanKha19, Proposition 2.2.13]. Therefore, by induction again, we need only check that ![]() $F \rightarrow \iota _*\iota ^*F$ is an equivalence on affine schemes which is tautologically true.
$F \rightarrow \iota _*\iota ^*F$ is an equivalence on affine schemes which is tautologically true.
We can now prove the following.
Theorem 3.5.9 The functor (40) extends canonically to a ![]() $\mathrm {sm}$-distributive functor
$\mathrm {sm}$-distributive functor
and, hence, to a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
Proof. First, by Lemma 3.5.8, the right Kan extension of the Nisnevich sheaf
to algebraic spaces defines a Nisnevich sheaf
Therefore, we can apply [Reference Bachmann and HoyoisBH21, Proposition C.18] to obtain an extension
of (40).
Now in order to use Theorem 2.5.1, we need to verify that this extension satisfies the distributivity property with respect to smooth morphisms. Since the functors involved in the adjointability and distributivity transformations are stable under base change, we are reduced to the case of schemes we discussed previously.
Remark 3.5.10 In the more general setting of spectral algebraic spaces, Khan has constructed the unstable motivic homotopy ![]() $\infty$-category (defined in [Reference KhanKha19, Definition 2.4.1]). By Nisnevich descent, this agrees with the right Kan extended version appearing in the proof of Theorem 3.5.9, using the uniqueness part of Lemma 3.5.8.
$\infty$-category (defined in [Reference KhanKha19, Definition 2.4.1]). By Nisnevich descent, this agrees with the right Kan extended version appearing in the proof of Theorem 3.5.9, using the uniqueness part of Lemma 3.5.8.
3.6 Bispans in spectral Deligne–Mumford stacks and  $\mathrm {Perf}$
$\mathrm {Perf}$
In this subsection we promote the functor ![]() $\mathrm {Perf}\colon \mathrm {SpDM} \rightarrow {\text {Cat}}_\infty$ to a functor out of an
$\mathrm {Perf}\colon \mathrm {SpDM} \rightarrow {\text {Cat}}_\infty$ to a functor out of an ![]() $(\infty,2)$-category of bispans. This extends a result of Barwick [Reference BarwickBar17, Example D], which gives a functor
$(\infty,2)$-category of bispans. This extends a result of Barwick [Reference BarwickBar17, Example D], which gives a functor
encoding the usual pullback ![]() $f^{*}$ and pushforward
$f^{*}$ and pushforward ![]() $f_{*}$ for a morphism in
$f_{*}$ for a morphism in ![]() $\mathrm {SpDM}$, with
$\mathrm {SpDM}$, with ![]() $\mathcal {FP}$ a class of morphisms for which
$\mathcal {FP}$ a class of morphisms for which ![]() $f_{*}$ restricts to perfect objects and satisfies base change. Our version adds a multiplicative pushforward
$f_{*}$ restricts to perfect objects and satisfies base change. Our version adds a multiplicative pushforward ![]() $f_{\otimes }$ where
$f_{\otimes }$ where ![]() $f$ is finite étale (at the cost of restricting the class
$f$ is finite étale (at the cost of restricting the class ![]() $\mathcal {FP}$ in order to guarantee the existence of Weil restrictions). We note that the multiplicative pushforward in this situation is right Kan extended from the symmetric monoidal structure in
$\mathcal {FP}$ in order to guarantee the existence of Weil restrictions). We note that the multiplicative pushforward in this situation is right Kan extended from the symmetric monoidal structure in ![]() $\mathrm {Perf}$ and is, thus, not as complicated as in the motivic and equivariant cases we considered previously. However, we include this section with a view towards applications in algebraic
$\mathrm {Perf}$ and is, thus, not as complicated as in the motivic and equivariant cases we considered previously. However, we include this section with a view towards applications in algebraic ![]() $K$-theory in the following section.
$K$-theory in the following section.
We will freely use the language of spectral Deligne–Mumford stacks introduced in [Reference LurieLur18]. We denote by ![]() $\mathrm {SpDM}_S$ the
$\mathrm {SpDM}_S$ the ![]() $\infty$-category of spectral Deligne–Mumford stacks over a base
$\infty$-category of spectral Deligne–Mumford stacks over a base ![]() $S$. We also adopt the following terminology from [Reference BarwickBar17, Example D].
$S$. We also adopt the following terminology from [Reference BarwickBar17, Example D].
Definition 3.6.1 Recall that for ![]() $X \in \mathrm {SpDM}$ an object
$X \in \mathrm {SpDM}$ an object ![]() $\mathcal {E} \in \mathrm {QCoh}(X)$ is called perfect if for every map
$\mathcal {E} \in \mathrm {QCoh}(X)$ is called perfect if for every map ![]() $x\colon \operatorname {Spec} A \rightarrow X$, where
$x\colon \operatorname {Spec} A \rightarrow X$, where ![]() $A$ is an
$A$ is an ![]() $E_{\infty }$-ring spectrum, the
$E_{\infty }$-ring spectrum, the ![]() $A$-module
$A$-module ![]() $x^*\mathcal {E}$ is perfect (i.e. dualizable or equivalently compact in the symmetric monoidal
$x^*\mathcal {E}$ is perfect (i.e. dualizable or equivalently compact in the symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() ${\text {Mod}}_{A}$). Now suppose that
${\text {Mod}}_{A}$). Now suppose that ![]() $f\colon X \rightarrow Y$ is a morphism in
$f\colon X \rightarrow Y$ is a morphism in ![]() $\mathrm {SpDM}$. We say that
$\mathrm {SpDM}$. We say that ![]() $f$ is perfect if the pushforward functor
$f$ is perfect if the pushforward functor
takes perfect objects to perfect objects.
The following theorem of Lurie furnishes a large class of perfect morphisms.
Theorem 3.6.2 [Reference LurieLur18, Theorem 6.1.3.2]
Let ![]() $f\colon X \rightarrow Y$ be a morphism in
$f\colon X \rightarrow Y$ be a morphism in ![]() $\mathrm {SpDM}$. If
$\mathrm {SpDM}$. If ![]() $f$ is proper, locally almost of finite presentation, and of finite Tor-amplitude, then
$f$ is proper, locally almost of finite presentation, and of finite Tor-amplitude, then ![]() $f$ is perfect.
$f$ is perfect.
Notation 3.6.3 Following [Reference BarwickBar17, Notation D.17], we label the class of morphisms in Theorem 3.6.2 by ![]() $\mathcal {FP}$.
$\mathcal {FP}$.
We will also make use the existence of the spectral version of Weil restriction; see the discussion of [Reference LurieLur18, § 19.1] and note that the definitions are completely analogous to the classical situation. There Lurie proves the following existence theorem.
Theorem 3.6.4 [Reference LurieLur18, Theorem 19.1.0.1]
Suppose that ![]() $f\colon X \rightarrow Y$ is a morphism in
$f\colon X \rightarrow Y$ is a morphism in ![]() $\mathrm {SpDM}$ that is proper, flat, and locally almost of finite presentation. Let
$\mathrm {SpDM}$ that is proper, flat, and locally almost of finite presentation. Let ![]() $p\colon Z \rightarrow X$ be a relative spectral algebraic space that is quasi-separated and locally almost of finite presentation. Then the Weil restriction
$p\colon Z \rightarrow X$ be a relative spectral algebraic space that is quasi-separated and locally almost of finite presentation. Then the Weil restriction ![]() $R_f(p) \in \mathrm {SpDM}_{Y}$ exists.
$R_f(p) \in \mathrm {SpDM}_{Y}$ exists.
Notation 3.6.5 In light of this, let us write:
•
 $\mathcal {W}$ for the class of morphisms in
$\mathcal {W}$ for the class of morphisms in  $\mathrm {SpDM}$ that are proper, flat, and locally almost of finite presentation;
$\mathrm {SpDM}$ that are proper, flat, and locally almost of finite presentation;•
 $\mathcal {Q}$ for the class of morphisms in
$\mathcal {Q}$ for the class of morphisms in  $\mathrm {SpDM}$ that are relative spectral algebraic spaces, quasi-separated, and locally almost of finite presentation;
$\mathrm {SpDM}$ that are relative spectral algebraic spaces, quasi-separated, and locally almost of finite presentation;•
 $\mathcal {FP}' \subset \mathcal {FP}$ for the class of morphisms in
$\mathcal {FP}' \subset \mathcal {FP}$ for the class of morphisms in  $\mathcal {FP}$ which are furthermore relative spectral algebraic spaces;
$\mathcal {FP}$ which are furthermore relative spectral algebraic spaces;•
 ${\text {f} {\unicode{x00E8}} \text{t}}$ for the class of finite étale morphisms in
${\text {f} {\unicode{x00E8}} \text{t}}$ for the class of finite étale morphisms in  $\mathrm {SpDM}$.
$\mathrm {SpDM}$.
Then Weil restrictions of morphisms in ![]() $\mathcal {Q}$ along ones in
$\mathcal {Q}$ along ones in ![]() $\mathcal {W}$ exist in
$\mathcal {W}$ exist in ![]() $\mathrm {SpDM}$. Here
$\mathrm {SpDM}$. Here ![]() $\mathcal {FP}' \subseteq \mathcal {Q}$ since proper morphisms are always quasi-separated, and
$\mathcal {FP}' \subseteq \mathcal {Q}$ since proper morphisms are always quasi-separated, and ![]() ${\text {f} {\unicode{x00E8}} \text{t}} \subseteq \mathcal {W}$.
${\text {f} {\unicode{x00E8}} \text{t}} \subseteq \mathcal {W}$.
Lemma 3.6.6 Suppose that ![]() $f\colon X \rightarrow Y$ is a morphism in
$f\colon X \rightarrow Y$ is a morphism in ![]() $\mathrm {SpDM}$ of class
$\mathrm {SpDM}$ of class ![]() $\mathcal {W}$ and
$\mathcal {W}$ and ![]() $p\colon Z \rightarrow X$ is one of class
$p\colon Z \rightarrow X$ is one of class ![]() $\mathcal {Q}$. Then
$\mathcal {Q}$. Then ![]() $R_{f}(p)$ is again of class
$R_{f}(p)$ is again of class ![]() $\mathcal {Q}$. Assuming
$\mathcal {Q}$. Assuming ![]() $f$ is moreover finite étale, we also have:
$f$ is moreover finite étale, we also have:
(a) if
 $p$ is quasi-compact, then
$p$ is quasi-compact, then  $R_f(p) \rightarrow Y$ is quasi-compact;
$R_f(p) \rightarrow Y$ is quasi-compact;(b) if
 $p$ is proper, then
$p$ is proper, then  $R_f(p) \rightarrow Y$ is proper;
$R_f(p) \rightarrow Y$ is proper;(c) if
 $p$ is of finite Tor-amplitude, then
$p$ is of finite Tor-amplitude, then  $R_f(p) \to Y$ is of finite Tor-amplitude.
$R_f(p) \to Y$ is of finite Tor-amplitude.
Proof. The statement that ![]() $R_{f}(p)$ is of class
$R_{f}(p)$ is of class ![]() $\mathcal {Q}$ is part of [Reference LurieLur18, Theorem 19.1.0.1].
$\mathcal {Q}$ is part of [Reference LurieLur18, Theorem 19.1.0.1].
Now let us verify properties (a)–(c). To verify properties (a) and (c), note that quasi-compactness and having finite Tor-amplitude can be detected étale locally on the target (for the former, this is [Reference LurieLur18, Remark 2.3.2.5] and the equivalences of [Reference LurieLur18, Proposition 2.3.2.1] and for the latter this is [Reference LurieLur18, Proposition 6.1.2.2]). Therefore, we may work étale locally on ![]() $Y$. Since
$Y$. Since ![]() $f$ was assumed to be finite étale, it is étale locally a fold map
$f$ was assumed to be finite étale, it is étale locally a fold map ![]() $f\colon X \simeq \coprod _{i=1}^{n} Y \rightarrow Y$. In this case, we can write
$f\colon X \simeq \coprod _{i=1}^{n} Y \rightarrow Y$. In this case, we can write ![]() $p \colon Z \rightarrow X$ as a coproduct
$p \colon Z \rightarrow X$ as a coproduct ![]() $\coprod _i f_i\colon \coprod _i Z_i \rightarrow \coprod _i Y$. Therefore, the Weil restriction takes the form
$\coprod _i f_i\colon \coprod _i Z_i \rightarrow \coprod _i Y$. Therefore, the Weil restriction takes the form ![]() $R_f(p) \simeq Z_1 \times _{Y} Z_2 \times _{Y} \cdots \times _Y Z_{n} \rightarrow Y$. To conclude property (a), we note that quasi-compactness is stable under base change [Reference LurieLur18, Proposition 2.3.3.1], while for property (c), we note that Tor-amplitudes add up under base change [Reference LurieLur18, Lemma 6.1.1.6].
$R_f(p) \simeq Z_1 \times _{Y} Z_2 \times _{Y} \cdots \times _Y Z_{n} \rightarrow Y$. To conclude property (a), we note that quasi-compactness is stable under base change [Reference LurieLur18, Proposition 2.3.3.1], while for property (c), we note that Tor-amplitudes add up under base change [Reference LurieLur18, Lemma 6.1.1.6].
To prove property (b), we use the valuative criterion for properness in the form [Reference LurieLur18, Corollary 5.3.1.2]. To apply this, we need to know that ![]() $R_{f}(p)$ is quasi-compact, quasi-separated, and locally of finite type. These properties follow from what we have already proved, since a morphism locally almost of finite presentation is also locally of finite type by [Reference LurieLur18, Remark 4.1.1.5]. The properness criterion of [Reference LurieLur18, Corollary 5.3.1.2] now follows from the functor-of-points description of the Weil restriction.
$R_{f}(p)$ is quasi-compact, quasi-separated, and locally of finite type. These properties follow from what we have already proved, since a morphism locally almost of finite presentation is also locally of finite type by [Reference LurieLur18, Remark 4.1.1.5]. The properness criterion of [Reference LurieLur18, Corollary 5.3.1.2] now follows from the functor-of-points description of the Weil restriction.
Proposition 3.6.7 Let ![]() $S$ be a spectral Deligne–Mumford stack. Then
$S$ be a spectral Deligne–Mumford stack. Then
is a bispan triple.
Proof. After Lemma 3.6.6 it suffices to note that morphisms in ![]() ${\text {f} {\unicode{x00E8}} \text{t}}$ and
${\text {f} {\unicode{x00E8}} \text{t}}$ and ![]() $\mathcal {FP}'$ are stable under base change. This follows from [Reference LurieLur18, Propositions 5.1.3.1, 4.2.1.6, 6.1.2.2, 1.4.1.11(2), and 3.3.1.8].
$\mathcal {FP}'$ are stable under base change. This follows from [Reference LurieLur18, Propositions 5.1.3.1, 4.2.1.6, 6.1.2.2, 1.4.1.11(2), and 3.3.1.8].
Theorem 3.6.8 Let ![]() $S$ be a spectral Deligne–Mumford stack. The functor
$S$ be a spectral Deligne–Mumford stack. The functor
canonically extends to a functor
Moreover, this is right ![]() $\mathcal {FP}'$-distributive (in the sense of Variant 2.4.12), and so canonically extends further to a functor of
$\mathcal {FP}'$-distributive (in the sense of Variant 2.4.12), and so canonically extends further to a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
Proof. We first apply [Reference Bachmann and HoyoisBH21, Proposition C.9] to extend ![]() $\mathrm {Perf}$ to a functor
$\mathrm {Perf}$ to a functor
where ![]() $\mathrm {SpDM}^{{\text {fold}}}_{S}$ consists of the finite fold maps, i.e. the maps
$\mathrm {SpDM}^{{\text {fold}}}_{S}$ consists of the finite fold maps, i.e. the maps ![]() $\coprod _{I}X \to \coprod _{J}X$ with
$\coprod _{I}X \to \coprod _{J}X$ with ![]() $I \to J$ a map of finite sets. Here the pushforward
$I \to J$ a map of finite sets. Here the pushforward
 \[ \nabla_{\otimes}\colon \mathrm{Perf}\bigg(\!\coprod_I X\!\bigg) \cong \mathrm{Perf}(X)^{\times I} \rightarrow \mathrm{Perf}(X) \]
\[ \nabla_{\otimes}\colon \mathrm{Perf}\bigg(\!\coprod_I X\!\bigg) \cong \mathrm{Perf}(X)^{\times I} \rightarrow \mathrm{Perf}(X) \]
is just the tensor product, and the base change simply encodes the fact that the pullback functors are symmetric monoidal.
Next, we use [Reference Bachmann and HoyoisBH21, Corollary C.13] for ![]() $\mathcal {C} = \mathrm {SpDM}$,
$\mathcal {C} = \mathrm {SpDM}$, ![]() $t$ the étale topology and
$t$ the étale topology and ![]() $m$ the class of finite étale maps to obtain a functor
$m$ the class of finite étale maps to obtain a functor
The content of this result is that since ![]() $\mathrm {Perf}$ is an étale sheaf and finite étale morphisms are étale-locally contained in the class of fold maps, we can extend the symmetric monoidal structure to norms along finite étale morphisms.
$\mathrm {Perf}$ is an étale sheaf and finite étale morphisms are étale-locally contained in the class of fold maps, we can extend the symmetric monoidal structure to norms along finite étale morphisms.
In order to show that this functor is right ![]() $\mathcal {FP}'$-distributive, we first check that its restriction
$\mathcal {FP}'$-distributive, we first check that its restriction ![]() $\mathrm {Perf} \colon \mathrm {SpDM}_{S} \to {\text {Cat}}_\infty$ is right
$\mathrm {Perf} \colon \mathrm {SpDM}_{S} \to {\text {Cat}}_\infty$ is right ![]() $\mathcal {FP}'$-adjointable. For any morphism
$\mathcal {FP}'$-adjointable. For any morphism ![]() $f \colon X \to Y$ in
$f \colon X \to Y$ in ![]() $\mathrm {SpDM}_{S}$ the functor
$\mathrm {SpDM}_{S}$ the functor ![]() $f^{*} \colon \mathrm {QCoh}(Y) \to \mathrm {QCoh}(Y)$ has a right adjoint
$f^{*} \colon \mathrm {QCoh}(Y) \to \mathrm {QCoh}(Y)$ has a right adjoint ![]() $f_{*}$. Given a pullback square
$f_{*}$. Given a pullback square

the commutative square

is right adjointable by [Reference LurieLur18, Corollary 3.4.2.2] provided ![]() $f$ is quasi-compact and quasi-separated. This is true by definition [Reference LurieLur18, Definition 5.1.2.1] for any proper morphism and so for any morphism in
$f$ is quasi-compact and quasi-separated. This is true by definition [Reference LurieLur18, Definition 5.1.2.1] for any proper morphism and so for any morphism in ![]() $\mathcal {FP}'$. Moreover, if
$\mathcal {FP}'$. Moreover, if ![]() $f$ is of finite Tor amplitude, then
$f$ is of finite Tor amplitude, then ![]() $f_{*}$ preserves perfect complexes by Theorem 3.6.2, so in this case the adjunction restricts to an adjunction
$f_{*}$ preserves perfect complexes by Theorem 3.6.2, so in this case the adjunction restricts to an adjunction
on the full subcategories of perfect objects, which still satisfies the right adjointability condition if ![]() $f$ is also quasi-compact and quasi-separated. This holds, in particular, if
$f$ is also quasi-compact and quasi-separated. This holds, in particular, if ![]() $f$ is in
$f$ is in ![]() $\mathcal {FP}'$, so that
$\mathcal {FP}'$, so that ![]() $\mathrm {Perf}$ is indeed right
$\mathrm {Perf}$ is indeed right ![]() $\mathcal {FP}'$-adjointable.
$\mathcal {FP}'$-adjointable.
It remains to check the (right) distributivity condition for ![]() $p \colon X\to Y$ in
$p \colon X\to Y$ in ![]() $\mathcal {FP}'$ and
$\mathcal {FP}'$ and ![]() $f \colon Y \to Z$ finite étale: given a distributivity diagram
$f \colon Y \to Z$ finite étale: given a distributivity diagram

the (right) distributivity transformation
must be invertible. Since ![]() $\mathrm {Perf}$ is an étale sheaf and distributivity transformations satisfy base change by Proposition 2.5.22, we may check this étale-locally on
$\mathrm {Perf}$ is an étale sheaf and distributivity transformations satisfy base change by Proposition 2.5.22, we may check this étale-locally on ![]() $Z$. Since finite étale morphisms are étale-locally given by finite fold maps, this means we may assume that
$Z$. Since finite étale morphisms are étale-locally given by finite fold maps, this means we may assume that ![]() $f$ is a fold map
$f$ is a fold map
 \[ \nabla \colon Y \simeq \coprod_{i=1}^{n} Z \to Z. \]
\[ \nabla \colon Y \simeq \coprod_{i=1}^{n} Z \to Z. \]
Since ![]() $\mathrm {SpDM}$ is extensive, we get a decomposition of
$\mathrm {SpDM}$ is extensive, we get a decomposition of ![]() $p$ as
$p$ as
 \[ \coprod_{i=1}^{n}p_{i} \colon \coprod_{i=1}^{n} X_{i} \to \coprod_{i=1}^{n} Z, \]
\[ \coprod_{i=1}^{n}p_{i} \colon \coprod_{i=1}^{n} X_{i} \to \coprod_{i=1}^{n} Z, \]
and an equivalence
since the universal property of ![]() $R_{\nabla }(p)$ is equivalent to that of this iterated fibre product:
$R_{\nabla }(p)$ is equivalent to that of this iterated fibre product:
 \begin{align*}
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}(W,R_{\nabla}(p))
& \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}(\nabla^{*}W,
X) \\ & \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}\bigg(\!\coprod_{i}
W, \coprod_{i} X_{i}\bigg) \\ & \simeq \prod_{i}
{\text {Map}}_{\mathrm{SpDM}_{S/Z}}(W,
X_{i}) \\ & \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/Z}}(W,
X_{1} \times_{Z} \cdots \times_{Z} X_{n}).
\end{align*}
\begin{align*}
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}(W,R_{\nabla}(p))
& \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}(\nabla^{*}W,
X) \\ & \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/\coprod_{i}Z}}\bigg(\!\coprod_{i}
W, \coprod_{i} X_{i}\bigg) \\ & \simeq \prod_{i}
{\text {Map}}_{\mathrm{SpDM}_{S/Z}}(W,
X_{i}) \\ & \simeq
{\text {Map}}_{\mathrm{SpDM}_{S/Z}}(W,
X_{1} \times_{Z} \cdots \times_{Z} X_{n}).
\end{align*}
If ![]() $\pi _{i}$ denotes the projection
$\pi _{i}$ denotes the projection ![]() $X_{1} \times _{Z} \cdots \times _{Z} X_{n} \to X_{i}$, then
$X_{1} \times _{Z} \cdots \times _{Z} X_{n} \to X_{i}$, then ![]() $\epsilon \simeq \coprod _{i} \pi _{i}$. Now given
$\epsilon \simeq \coprod _{i} \pi _{i}$. Now given ![]() $\mathcal {F} \in \mathrm {Perf}(X)$ corresponding to
$\mathcal {F} \in \mathrm {Perf}(X)$ corresponding to ![]() $\mathcal {F}_{i} \in \mathrm {Perf}(X_{i})$ under the equivalence
$\mathcal {F}_{i} \in \mathrm {Perf}(X_{i})$ under the equivalence ![]() $\mathrm {Perf}(X) \simeq \prod _{i} \mathrm {Perf}(X_{i})$, we can write
$\mathrm {Perf}(X) \simeq \prod _{i} \mathrm {Perf}(X_{i})$, we can write
with the distributivity map ![]() $\nabla _{\otimes }p_{*}\mathcal {F} \to g_{*}\tilde {\nabla }_{\otimes }\epsilon ^{*}\mathcal {F}$ given by the composite
$\nabla _{\otimes }p_{*}\mathcal {F} \to g_{*}\tilde {\nabla }_{\otimes }\epsilon ^{*}\mathcal {F}$ given by the composite
 \begin{align*} p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes p_{n,*}\mathcal{F}_{n} & \to g_{*}g^{*}(p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes p_{n,*}\mathcal{F}_{n}) \\ & \simeq g_{*}(g^{*}p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes g^{*}p_{n,*}\mathcal{F}_{n}) \\ & \simeq g_{*}(\pi_{1}^{*}p_{1}^{*}p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes \pi_{n}^{*}p_{n}^{*}p_{n,*}\mathcal{F}_{n})\\ & \to g_{*}(\pi_{1}^{*}\mathcal{F}_{1} \otimes \cdots \otimes \pi_{n}^{*}\mathcal{F}_{n}). \end{align*}
\begin{align*} p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes p_{n,*}\mathcal{F}_{n} & \to g_{*}g^{*}(p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes p_{n,*}\mathcal{F}_{n}) \\ & \simeq g_{*}(g^{*}p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes g^{*}p_{n,*}\mathcal{F}_{n}) \\ & \simeq g_{*}(\pi_{1}^{*}p_{1}^{*}p_{1,*}\mathcal{F}_{1} \otimes \cdots \otimes \pi_{n}^{*}p_{n}^{*}p_{n,*}\mathcal{F}_{n})\\ & \to g_{*}(\pi_{1}^{*}\mathcal{F}_{1} \otimes \cdots \otimes \pi_{n}^{*}\mathcal{F}_{n}). \end{align*}
That this is an equivalence now follows from base change and the projection formula (which applies for maps in ![]() $\mathcal {FP}'$ by [Reference LurieLur18, Remark 3.4.2.6]). To keep the notation bearable we spell this out only in the case
$\mathcal {FP}'$ by [Reference LurieLur18, Remark 3.4.2.6]). To keep the notation bearable we spell this out only in the case ![]() $n = 2$, where it follows from Remark 2.4.11 that the distributivity condition is equivalent to the following commutative square being right adjointable (where
$n = 2$, where it follows from Remark 2.4.11 that the distributivity condition is equivalent to the following commutative square being right adjointable (where ![]() $V:= X_{1} \times _{Z} X_{2}$):
$V:= X_{1} \times _{Z} X_{2}$):

We can decompose this diagram as follows:

Since horizontal and vertical pastings of right adjointable squares are again right adjointable, it suffices to check that the three smaller squares in this diagram are all right adjointable. This is true since the mate of the left square is the projection formula transformation for ![]() $p_{1}$,
$p_{1}$,
while the mate of the bottom right square is the projection formula transformation for ![]() $\pi _{1}$, and finally the mate of the top right square is
$\pi _{1}$, and finally the mate of the top right square is ![]() ${\text {id}}_{\mathrm {Perf}(X_{1})}$ times the base change transformation
${\text {id}}_{\mathrm {Perf}(X_{1})}$ times the base change transformation
corresponding to the pullback square

We have shown that the functor
is right ![]() $\mathcal {FP}'$-adjointable, and it therefore extends canonically to a functor of
$\mathcal {FP}'$-adjointable, and it therefore extends canonically to a functor of ![]() $(\infty,2)$-categories
$(\infty,2)$-categories
by Theorem 2.5.1.
4. Norms in algebraic  $K$-theory
$K$-theory
4.1 Algebraic  $K$-theory and polynomial functors
$K$-theory and polynomial functors
Our goal in this final section is to combine our results so far with recent work of Barwick, Glasman, Mathew, and Nikolaus [Reference Barwick, Glasman, Mathew and NikolausBGMN21] in order to construct additional structure on algebraic ![]() $K$-theory spectra. In this subsection we will review the polynomial functoriality of
$K$-theory spectra. In this subsection we will review the polynomial functoriality of ![]() $K$-theory constructed in [Reference Barwick, Glasman, Mathew and NikolausBGMN21].
$K$-theory constructed in [Reference Barwick, Glasman, Mathew and NikolausBGMN21].
Assume that ![]() $\mathcal {C}, \mathcal {D}$ are small
$\mathcal {C}, \mathcal {D}$ are small ![]() $\infty$-categories; a functor
$\infty$-categories; a functor
is then to be a polynomial functor if it is ![]() $n$-excisive in the sense of Goodwillie calculus [Reference GoodwillieGoo91] for some
$n$-excisive in the sense of Goodwillie calculus [Reference GoodwillieGoo91] for some ![]() $n$. For our purposes it is more convenient to follow the inductive definition in [Reference Barwick, Glasman, Mathew and NikolausBGMN21, Definitions 2.4 and 2.11], which is based on work of Eilenberg and Maclane [Reference Eilenberg and Mac LaneEML54]:
$n$. For our purposes it is more convenient to follow the inductive definition in [Reference Barwick, Glasman, Mathew and NikolausBGMN21, Definitions 2.4 and 2.11], which is based on work of Eilenberg and Maclane [Reference Eilenberg and Mac LaneEML54]:
Definition 4.1.1 Let ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $\mathcal {B}$ be additive
$\mathcal {B}$ be additive ![]() $\infty$-categories and assume that
$\infty$-categories and assume that ![]() $\mathcal {B}$ is idempotent-complete. Then we inductively define what it means for a functor
$\mathcal {B}$ is idempotent-complete. Then we inductively define what it means for a functor ![]() $F \colon \mathcal {A} \rightarrow \mathcal {B}$ to be polynomial of degree
$F \colon \mathcal {A} \rightarrow \mathcal {B}$ to be polynomial of degree ![]() $\leq n$:
$\leq n$:
• if
 $n = -1$, then
$n = -1$, then  $f$ must be the zero functor;
$f$ must be the zero functor;• if
 $n = 0$, then
$n = 0$, then  $f$ must be constant;
$f$ must be constant;• if
 $n > 0$, then for each fixed
$n > 0$, then for each fixed  $x \in \mathcal {A}$, the functor
must be polynomial of degree
$x \in \mathcal {A}$, the functor
must be polynomial of degree \[ D_x(f): \mathcal{A} \rightarrow \mathcal{B}, \quad y \mapsto \mathrm{Fib}(F(x \oplus y) \rightarrow F(y)), \]
\[ D_x(f): \mathcal{A} \rightarrow \mathcal{B}, \quad y \mapsto \mathrm{Fib}(F(x \oplus y) \rightarrow F(y)), \]
 $\leq n-1$ (this fibre exists since
$\leq n-1$ (this fibre exists since  $\mathcal {B}$ is assumed to be idempotent-complete: it is the complementary summand to
$\mathcal {B}$ is assumed to be idempotent-complete: it is the complementary summand to  $F(y)$ in
$F(y)$ in  $F(x \oplus y)$).
$F(x \oplus y)$).
Remark 4.1.2 Via the comparison result of [Reference Barwick, Glasman, Mathew and NikolausBGMN21, Proposition 2.15], this definition of polynomial functors agrees with the one via Goodwillie calculus for all idempotent-complete stable ![]() $\infty$-categories.
$\infty$-categories.
Warning 4.1.3 The notion of polynomial functor from Definition 4.1.1, which makes sense in additive contexts, is completely unrelated to the concept with the same name that we considered in Definition 3.3.3, which only exists for slices of the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {S}$.
$\mathcal {S}$.
Remark 4.1.4 Any exact functor between stable ![]() $\infty$-categories is polynomial of degree
$\infty$-categories is polynomial of degree ![]() $\leq 1$. Note that this applies in particular to any functor that has a left or right adjoint.
$\leq 1$. Note that this applies in particular to any functor that has a left or right adjoint.
Proposition 4.1.5 Suppose ![]() $F,G \colon \mathcal {C} \to \mathcal {D}$ are polynomial of degree
$F,G \colon \mathcal {C} \to \mathcal {D}$ are polynomial of degree ![]() $\leq n$. Then
$\leq n$. Then ![]() $F \oplus G \colon \mathcal {C} \to \mathcal {D}$ is also polynomial of degree
$F \oplus G \colon \mathcal {C} \to \mathcal {D}$ is also polynomial of degree ![]() $\leq n$.
$\leq n$.
Proof. This is a special case of [Reference Bachmann and HoyoisBH21, Lemma 5.24(3)].
Definition 4.1.6 We have the (non-full) subcategory
whose objects are the small, idempotent-complete stable ![]() $\infty$-categories and whose morphisms are the polynomial functors between them.
$\infty$-categories and whose morphisms are the polynomial functors between them.
Recall that (connective) algebraic ![]() $K$-theory can be defined as a functor from stable
$K$-theory can be defined as a functor from stable ![]() $\infty$-categories to spectra. Passing to the underlying infinite loop spaces, we get a functor
$\infty$-categories to spectra. Passing to the underlying infinite loop spaces, we get a functor
where ![]() ${\text {Cat}}_\infty ^{\mathrm {stab}}$ denotes the
${\text {Cat}}_\infty ^{\mathrm {stab}}$ denotes the ![]() $\infty$-category of stable
$\infty$-category of stable ![]() $\infty$-categories and exact functors. This is equipped with a transformation
$\infty$-categories and exact functors. This is equipped with a transformation ![]() $(-)^{\simeq } \rightarrow \Omega ^{\infty }K$ that exhibits
$(-)^{\simeq } \rightarrow \Omega ^{\infty }K$ that exhibits ![]() $\Omega ^{\infty }K$ as the universal additivization of
$\Omega ^{\infty }K$ as the universal additivization of ![]() $(-)^{\simeq }$ in the sense of [Reference BarwickBar16, Reference Blumberg, Gepner and TabuadaBGT13]. The main result of [Reference Barwick, Glasman, Mathew and NikolausBGMN21] shows that if we restrict to the full subcategory
$(-)^{\simeq }$ in the sense of [Reference BarwickBar16, Reference Blumberg, Gepner and TabuadaBGT13]. The main result of [Reference Barwick, Glasman, Mathew and NikolausBGMN21] shows that if we restrict to the full subcategory ![]() ${\text {Cat}}_\infty ^{\mathrm {stab},{\text {idem}}}$ of idempotent-complete stable
${\text {Cat}}_\infty ^{\mathrm {stab},{\text {idem}}}$ of idempotent-complete stable ![]() $\infty$-categories, then we can extend this to be functorial in all polynomial functors (rather than only the exact ones).
$\infty$-categories, then we can extend this to be functorial in all polynomial functors (rather than only the exact ones).
Theorem 4.1.7 (Barwick, Glasman, Mathew, and Nikolaus)
The space-valued ![]() $K$-theory functor extends to a functor
$K$-theory functor extends to a functor ![]() $\Omega ^{\infty }K^{\mathrm {poly}} \colon {\text {Cat}}_\infty ^{\mathrm {poly}} \rightarrow \mathcal {S}$ rendering the following diagram commutative:
$\Omega ^{\infty }K^{\mathrm {poly}} \colon {\text {Cat}}_\infty ^{\mathrm {poly}} \rightarrow \mathcal {S}$ rendering the following diagram commutative:

(We will usually just refer to this extension as ![]() $\Omega ^{\infty }K$.)
$\Omega ^{\infty }K$.)
We want to apply this to construct additional norms in ![]() $K$-theory, in the following way.
$K$-theory, in the following way.
Corollary 4.1.8 Suppose ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple, and that
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is a bispan triple, and that ![]() $\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ is a functor such that:
$\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ is a functor such that:
(1)
 $\Phi (X)$ is an idempotent-complete stable
$\Phi (X)$ is an idempotent-complete stable  $\infty$-category for every
$\infty$-category for every  $X \in \mathcal {C}$;
$X \in \mathcal {C}$;(2)
 $f^{\circledast } \colon \Phi (Y) \to \Phi (X)$ is a polynomial functor for every
$f^{\circledast } \colon \Phi (Y) \to \Phi (X)$ is a polynomial functor for every  $f \colon X \to Y$ in
$f \colon X \to Y$ in  $\mathcal {C}$;
$\mathcal {C}$;(3)
 $f_{\otimes } \colon \Phi (X) \to \Phi (Y)$ is a polynomial functor for every
$f_{\otimes } \colon \Phi (X) \to \Phi (Y)$ is a polynomial functor for every  $f \colon X \to Y$ in
$f \colon X \to Y$ in  $\mathcal {C}_{F}$;
$\mathcal {C}_{F}$;(4)
 $\Phi$ is
$\Phi$ is  $L$-distributive.
$L$-distributive.
Then ![]() $\Phi$ induces a functor
$\Phi$ induces a functor
which takes ![]() $X \in \mathcal {C}$ to
$X \in \mathcal {C}$ to ![]() $\Omega ^{\infty }K(\Phi (X))$.
$\Omega ^{\infty }K(\Phi (X))$.
Proof. Since ![]() $\Phi$ is
$\Phi$ is ![]() $L$-distributive, it extends to a functor
$L$-distributive, it extends to a functor ![]() ${\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$ by Theorem 2.5.1. The induced functor
${\text {BISPAN}}_{F,L}(\mathcal {C}) \to {\text {CAT}}_{\infty }$ by Theorem 2.5.1. The induced functor ![]() ${\text {Bispan}}_{F,L}(\mathcal {C}) \to {\text {Cat}}_\infty$ on underlying
${\text {Bispan}}_{F,L}(\mathcal {C}) \to {\text {Cat}}_\infty$ on underlying ![]() $\infty$-categories then factors through the subcategory
$\infty$-categories then factors through the subcategory ![]() ${\text {Cat}}_\infty ^{\mathrm {poly}}$: on objects and for the maps of the form
${\text {Cat}}_\infty ^{\mathrm {poly}}$: on objects and for the maps of the form ![]() $f^{\circledast }$ and
$f^{\circledast }$ and ![]() $f_{\otimes }$ this is true by assumption, and for
$f_{\otimes }$ this is true by assumption, and for ![]() $f_{\oplus }$ because this is a left adjoint and so polynomial by Remark 4.1.4. We can then combine the resulting functor with that of Theorem 4.1.7 to complete the proof.
$f_{\oplus }$ because this is a left adjoint and so polynomial by Remark 4.1.4. We can then combine the resulting functor with that of Theorem 4.1.7 to complete the proof.
Remark 4.1.9 If ![]() $\mathcal {C}_{L} = \mathcal {C}$, then condition (2) is automatic, since
$\mathcal {C}_{L} = \mathcal {C}$, then condition (2) is automatic, since ![]() $f^{\circledast }$ is a right adjoint for all
$f^{\circledast }$ is a right adjoint for all ![]() $f$.
$f$.
4.2 Polynomial functors from distributivity
In order to apply Corollary 4.1.8 in practice, we need to know that the functors ![]() $p_{\otimes }$ are polynomial for
$p_{\otimes }$ are polynomial for ![]() $p$ in
$p$ in ![]() $\mathcal {C}_{F}$. Our goal in this section is to derive a convenient criterion for this using distributivity, by generalizing an argument due to Bachmann and Hoyois [Reference Bachmann and HoyoisBH21, § 5.5]. We start by introducing some conditions and extra structure on bispan triples.
$\mathcal {C}_{F}$. Our goal in this section is to derive a convenient criterion for this using distributivity, by generalizing an argument due to Bachmann and Hoyois [Reference Bachmann and HoyoisBH21, § 5.5]. We start by introducing some conditions and extra structure on bispan triples.
Definition 4.2.1 A span pair ![]() $(\mathcal {C}, \mathcal {C}_F)$ is said to be an extensive span pair if:
$(\mathcal {C}, \mathcal {C}_F)$ is said to be an extensive span pair if:
(1) the
 $\infty$-category
$\infty$-category  $\mathcal {C}$ is extensive;
$\mathcal {C}$ is extensive;(2)
 $\mathcal {C}_F$ is closed under coproducts;
$\mathcal {C}_F$ is closed under coproducts;(3) for any
 $x \in \mathcal {C}$ the unique morphism
$x \in \mathcal {C}$ the unique morphism  $\emptyset \rightarrow x$ is in
$\emptyset \rightarrow x$ is in  $\mathcal {C}_{F}$;
$\mathcal {C}_{F}$;(4) for any
 $x\in \mathcal {C}$ the fold map
$x\in \mathcal {C}$ the fold map  $\nabla \colon x \coprod x \rightarrow x$ is in
$\nabla \colon x \coprod x \rightarrow x$ is in  $\mathcal {C}_F$.
$\mathcal {C}_F$.
Remark 4.2.2 If ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is an extensive span pair, then the symmetric monoidal structure on
$(\mathcal {C}, \mathcal {C}_{F})$ is an extensive span pair, then the symmetric monoidal structure on ![]() $\operatorname {Span}_{F}(\mathcal {C})$ induced by the coproduct in
$\operatorname {Span}_{F}(\mathcal {C})$ induced by the coproduct in ![]() $\mathcal {C}$ via Example 2.6.9 is both cartesian and cocartesian. In other words, in this case the coproduct in
$\mathcal {C}$ via Example 2.6.9 is both cartesian and cocartesian. In other words, in this case the coproduct in ![]() $\mathcal {C}$ gives both the product and coproduct in
$\mathcal {C}$ gives both the product and coproduct in ![]() $\operatorname {Span}_{F}(\mathcal {C})$.
$\operatorname {Span}_{F}(\mathcal {C})$.
Definition 4.2.3 Suppose ![]() $(\mathcal {C}, \mathcal {C}_F)$ is an extensive span pair. Then a degree structure on
$(\mathcal {C}, \mathcal {C}_F)$ is an extensive span pair. Then a degree structure on ![]() $(\mathcal {C}, \mathcal {C}_F)$ consists of a collection of morphisms
$(\mathcal {C}, \mathcal {C}_F)$ consists of a collection of morphisms ![]() $F_{n} \subseteq {\text {Map}}([1], \mathcal {C}_{F})$ for each
$F_{n} \subseteq {\text {Map}}([1], \mathcal {C}_{F})$ for each ![]() $n \in \mathbb {N}$, called morphisms of degree
$n \in \mathbb {N}$, called morphisms of degree ![]() $n$, such that:
$n$, such that:
(1) for each morphism
 $f\colon x \rightarrow y$ in
$f\colon x \rightarrow y$ in  $\mathcal {C}_F$, there exists a natural number
$\mathcal {C}_F$, there exists a natural number  $N < \infty$ and an essentially unique (finite) coproduct decomposition (called the degree decomposition)
such that for each
$N < \infty$ and an essentially unique (finite) coproduct decomposition (called the degree decomposition)
such that for each \[ y \simeq \coprod^N_{n=0} y_n^{(f)}, \]
\[ y \simeq \coprod^N_{n=0} y_n^{(f)}, \]
 $0 \leq n \leq N$, the morphism
is of degree
$0 \leq n \leq N$, the morphism
is of degree \[ f_n:=f \times_y y_n^{(f)}\colon x^{(f)}_n = x \times_y y_n^{(f)} \to y_n^{(f)} \]
\[ f_n:=f \times_y y_n^{(f)}\colon x^{(f)}_n = x \times_y y_n^{(f)} \to y_n^{(f)} \]
 $n$;
$n$;(2) the collection
 $F_{0}$ consists of the morphisms
$F_{0}$ consists of the morphisms  $\emptyset \rightarrow X$;
$\emptyset \rightarrow X$;(3) morphisms in
 $F_n$ are stable under base change: if
$F_n$ are stable under base change: if  $f\colon x \rightarrow y$ is degree
$f\colon x \rightarrow y$ is degree  $n$, then for any
$n$, then for any  $w \rightarrow y$, the morphism
$w \rightarrow y$, the morphism  $w \times _y x \rightarrow w$ is also of degree
$w \times _y x \rightarrow w$ is also of degree  $n$;
$n$;(4) given morphisms
 $f\colon x \rightarrow y, g\colon z \rightarrow y$ in
$f\colon x \rightarrow y, g\colon z \rightarrow y$ in  $\mathcal {C}_F$ which are of degrees
$\mathcal {C}_F$ which are of degrees  $n$ and
$n$ and  $m$, respectively, then the morphism
in
$m$, respectively, then the morphism
in \[ x \coprod z \xrightarrow{f \coprod g} y \coprod y \xrightarrow{\nabla} y \]
\[ x \coprod z \xrightarrow{f \coprod g} y \coprod y \xrightarrow{\nabla} y \]
 $\mathcal {C}_F$ is of degree
$\mathcal {C}_F$ is of degree  $m + n$;
$m + n$;(5) if
 $n \not = m$, then
$n \not = m$, then
 \[ F_n \cap F_m = \{ \emptyset \rightarrow \emptyset \}. \]
\[ F_n \cap F_m = \{ \emptyset \rightarrow \emptyset \}. \]
Furthermore, given a degree structure, we say a morphism ![]() $f \colon x \to y$ is of degree
$f \colon x \to y$ is of degree ![]() $\leq n$ if in the degree decomposition we have
$\leq n$ if in the degree decomposition we have ![]() $y_{i}^{(f)} \simeq \emptyset$ for
$y_{i}^{(f)} \simeq \emptyset$ for ![]() $i > n$. We also say that a morphism is of degree
$i > n$. We also say that a morphism is of degree ![]() $-1$ if it is the essentially unique morphism
$-1$ if it is the essentially unique morphism ![]() $\emptyset \rightarrow \emptyset$. Lastly, we say that a morphism
$\emptyset \rightarrow \emptyset$. Lastly, we say that a morphism ![]() $f \colon x \to y$ is surjective if
$f \colon x \to y$ is surjective if ![]() $y_0^{(f)} = \emptyset$.
$y_0^{(f)} = \emptyset$.
Remark 4.2.4 Suppose that ![]() $(\mathcal {C}, \mathcal {C}_F)$ is equipped with a degree structure. We note that not all morphisms have a well-defined degree although each morphism does have a degree decomposition. In addition, the reader is encouraged to think of
$(\mathcal {C}, \mathcal {C}_F)$ is equipped with a degree structure. We note that not all morphisms have a well-defined degree although each morphism does have a degree decomposition. In addition, the reader is encouraged to think of ![]() $x^{(f)}_0$ as the ‘locus’ in
$x^{(f)}_0$ as the ‘locus’ in ![]() $x$ where
$x$ where ![]() $f$ has empty fibres, i.e. fails to be surjective.
$f$ has empty fibres, i.e. fails to be surjective.
Lemma 4.2.5 Given a degree structure on ![]() $(\mathcal {C}, \mathcal {C}_F)$, then:
$(\mathcal {C}, \mathcal {C}_F)$, then:
(1) surjective morphisms are stable under pullbacks;
(2) if
 $f\colon \emptyset \to y$ is a surjective morphism, then
$f\colon \emptyset \to y$ is a surjective morphism, then  $y \simeq \emptyset$.
$y \simeq \emptyset$.
Proof. To prove part (1), assume that ![]() $f\colon x \rightarrow y$ is a morphism with a degree decomposition
$f\colon x \rightarrow y$ is a morphism with a degree decomposition ![]() $y \simeq \coprod ^N_{n=0} y_n^{(f)}$. If
$y \simeq \coprod ^N_{n=0} y_n^{(f)}$. If ![]() $g\colon z \to y$ is another morphism, then from Definition 4.2.3(3) and the uniqueness of the degree decomposition, we have that the degree decomposition of the base change
$g\colon z \to y$ is another morphism, then from Definition 4.2.3(3) and the uniqueness of the degree decomposition, we have that the degree decomposition of the base change
is given by ![]() $z \simeq \coprod ^N_{n=0} (z \times _{y} y_n^{(f)})$. The degree
$z \simeq \coprod ^N_{n=0} (z \times _{y} y_n^{(f)})$. The degree ![]() $0$ part of
$0$ part of ![]() $f'$ is, thus,
$f'$ is, thus,
as required.
Next we prove part (2). Let ![]() $y \simeq \coprod ^N_{n=0} y_n^{(f)}$ be the degree decomposition of
$y \simeq \coprod ^N_{n=0} y_n^{(f)}$ be the degree decomposition of ![]() $f$. Then the map
$f$. Then the map ![]() $\emptyset \simeq \emptyset \times _{y} y_{n}^{(f)} \to y_{n}^{(f)}$ has degree
$\emptyset \simeq \emptyset \times _{y} y_{n}^{(f)} \to y_{n}^{(f)}$ has degree ![]() $n$, but by Definition 4.2.3(2) it also has degree
$n$, but by Definition 4.2.3(2) it also has degree ![]() $0$; hence, by Definition 4.2.3(5) we must have
$0$; hence, by Definition 4.2.3(5) we must have ![]() $y_{n}^{(f)} \simeq \emptyset$ for
$y_{n}^{(f)} \simeq \emptyset$ for ![]() $n > 0$. Since, by assumption, we also have
$n > 0$. Since, by assumption, we also have ![]() $y_{0}^{(f)} \simeq \emptyset$, we must have
$y_{0}^{(f)} \simeq \emptyset$, we must have ![]() $y \simeq \emptyset$.
$y \simeq \emptyset$.
Example 4.2.6 Here are the main examples of degree structures on the span pairs that have appeared throughout this paper.
(1) Consider the extensive span pair
 $(\mathbb {F}, \mathbb {F})$. There is a degree structure where a morphism of finite sets
$(\mathbb {F}, \mathbb {F})$. There is a degree structure where a morphism of finite sets  $f\colon X \rightarrow Y$ is of degree
$f\colon X \rightarrow Y$ is of degree  $n$ when the fibres all have cardinality exactly
$n$ when the fibres all have cardinality exactly  $n$.
$n$.(2) Consider the extensive span pair
 $(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$. There is a degree structure where a morphism
$(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$. There is a degree structure where a morphism  $f\colon X \rightarrow Y$ in
$f\colon X \rightarrow Y$ in  $\mathcal {S}_{\mathrm {fin}}$ is of degree
$\mathcal {S}_{\mathrm {fin}}$ is of degree  $n$ if all its fibres have cardinality exactly
$n$ if all its fibres have cardinality exactly  $n$.
$n$.(3) Consider the extensive span pair
 $(\mathbb {F}_{G}, \mathbb {F}_{G})$. Then we say that morphism of finite
$(\mathbb {F}_{G}, \mathbb {F}_{G})$. Then we say that morphism of finite  $G$-sets
$G$-sets  $f\colon X \rightarrow Y$ is of degree
$f\colon X \rightarrow Y$ is of degree  $n$ when (the underlying sets of) the fibres all have cardinality exactly
$n$ when (the underlying sets of) the fibres all have cardinality exactly  $n$.
$n$.(4) Consider the extensive algebro-geometric span pairs
 $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}})$,
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{{\text {flf}}})$,  $(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}})$,
$(\mathrm {Sch}_{S}, \mathrm {Sch}_{S}^{\text {f} {\unicode{x00E8}} \text{t}})$,  $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}})$,
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{{\text {flf}}})$,  $(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}})$, and
$(\mathrm {AlgSpc}_{S}, \mathrm {AlgSpc}_{S}^{\text {f} {\unicode{x00E8}} \text{t}})$, and  $(\mathrm {SpDM}_S, \mathrm {SpDM}^{\text {f} {\unicode{x00E8}} \text{t}}_S)$. In each of these, the degree of a morphism
$(\mathrm {SpDM}_S, \mathrm {SpDM}^{\text {f} {\unicode{x00E8}} \text{t}}_S)$. In each of these, the degree of a morphism  $f\colon X \rightarrow Y$ can be defined to be
$f\colon X \rightarrow Y$ can be defined to be  $n$ if the sheaf of finite, locally free
$n$ if the sheaf of finite, locally free  $\mathcal {O}_Y$-modules given by
$\mathcal {O}_Y$-modules given by  $f_*(\mathcal {O}_X)$ is of constant rank
$f_*(\mathcal {O}_X)$ is of constant rank  $n$.
$n$.
Remark 4.2.7 In all the examples from Example 4.2.6, the degree 1 morphisms are precisely the equivalences. This is not assumed for a general degree structure since we do not need it for our main results.
Construction 4.2.8 We will need to compute how the degree decomposition interacts with coproducts of morphisms. Thus, let ![]() $f\colon x \rightarrow y, g\colon z \rightarrow y$ be two morphisms. Each morphism then induces a coproduct decomposition (where the index runs through a finite set)
$f\colon x \rightarrow y, g\colon z \rightarrow y$ be two morphisms. Each morphism then induces a coproduct decomposition (where the index runs through a finite set)
We set
From this, we can form the following diagram where each square is cartesian:

Lemma 4.2.9 Let ![]() $(\mathcal {C}, \mathcal {C}_F)$ be an extensive pair with a degree structure. Let
$(\mathcal {C}, \mathcal {C}_F)$ be an extensive pair with a degree structure. Let ![]() $f\colon x \rightarrow y, g\colon z \rightarrow y$ be two morphisms in
$f\colon x \rightarrow y, g\colon z \rightarrow y$ be two morphisms in ![]() $\mathcal {C}_F$. Then in the degree decomposition of the map
$\mathcal {C}_F$. Then in the degree decomposition of the map ![]() $\nabla _y \circ (f \amalg g) \colon x \amalg z \rightarrow y$, the degree-
$\nabla _y \circ (f \amalg g) \colon x \amalg z \rightarrow y$, the degree-![]() $k$ component is
$k$ component is
where ![]() $z_{mn} \rightarrow y_{mn}$ is of degree
$z_{mn} \rightarrow y_{mn}$ is of degree ![]() $m$ and
$m$ and ![]() $x_{mn} \rightarrow y_{mn}$ is of degree
$x_{mn} \rightarrow y_{mn}$ is of degree ![]() $n$.
$n$.
Proof. Since coproduct decompositions are stable under pullbacks we have that for each ![]() $n \in \mathbb {N}$,
$n \in \mathbb {N}$,
By Definition 4.2.3(3) the pullback ![]() $x_{mn} \to y_{mn}$ of
$x_{mn} \to y_{mn}$ of ![]() $f$ is therefore also of degree
$f$ is therefore also of degree ![]() $n$. Similarly, the pullback of
$n$. Similarly, the pullback of ![]() $g$ to
$g$ to ![]() $z_{mn} \to y_{mn}$ is of degree
$z_{mn} \to y_{mn}$ is of degree ![]() $m$, and so by Definition 4.2.3(4) the composite
$m$, and so by Definition 4.2.3(4) the composite
is of degree ![]() $m+n$. Now note that we have
$m+n$. Now note that we have
Here ![]() $\nabla _{y} \circ (f \amalg g)$ restricts over
$\nabla _{y} \circ (f \amalg g)$ restricts over ![]() $y_{mn}$ to the map
$y_{mn}$ to the map ![]() $x_{mn} \amalg z_{mn} \to y_{mn}$ of degree
$x_{mn} \amalg z_{mn} \to y_{mn}$ of degree ![]() $m+n$, so this is a decomposition into components of fixed degree; by uniqueness this is therefore the degree composition.
$m+n$, so this is a decomposition into components of fixed degree; by uniqueness this is therefore the degree composition.
The purpose of a degree structure as in Definition 4.2.3 is to allow us to prove that certain functors are polynomial by induction on degrees using distributivity, by abstracting the arguments in [Reference Bachmann and HoyoisBH21, § 5.5].
Definition 4.2.10 We say a bispan triple ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple if both
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple if both ![]() $(\mathcal {C},\mathcal {C}_{F})$ and
$(\mathcal {C},\mathcal {C}_{F})$ and ![]() $(\mathcal {C},\mathcal {C}_{L})$ are extensive span pairs.
$(\mathcal {C},\mathcal {C}_{L})$ are extensive span pairs.
Remark 4.2.11 If ![]() $(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple, then the symmetric monoidal structure on
$(\mathcal {C}, \mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple, then the symmetric monoidal structure on ![]() ${\text {Bispan}}_{F,L}(\mathcal {C})$ induced by the coproduct in
${\text {Bispan}}_{F,L}(\mathcal {C})$ induced by the coproduct in ![]() $\mathcal {C}$ as in Example 2.6.12 is cartesian, i.e. the coproduct in
$\mathcal {C}$ as in Example 2.6.12 is cartesian, i.e. the coproduct in ![]() $\mathcal {C}$ gives a product in
$\mathcal {C}$ gives a product in ![]() ${\text {Bispan}}_{F,L}(\mathcal {C})$.
${\text {Bispan}}_{F,L}(\mathcal {C})$.
Definition 4.2.12 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple where
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple where ![]() $\mathcal {C}$ is idempotent-complete. For
$\mathcal {C}$ is idempotent-complete. For ![]() $p \colon y \to z$ in
$p \colon y \to z$ in ![]() $\mathcal {C}_{F}$, we say that
$\mathcal {C}_{F}$, we say that ![]() $p_{*}$ preserves summand inclusions if given any maps
$p_{*}$ preserves summand inclusions if given any maps ![]() $x,x' \to y$ the morphism
$x,x' \to y$ the morphism ![]() $p_{*}x \to p_{*}(x \amalg x')$ is a summand inclusion in the sense that there exists a morphism
$p_{*}x \to p_{*}(x \amalg x')$ is a summand inclusion in the sense that there exists a morphism ![]() $c \to p_{*}(x \amalg x')$ such that
$c \to p_{*}(x \amalg x')$ such that
is an equivalence.
Lemma 4.2.13 Suppose ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple where
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ is an extensive bispan triple where ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is equipped with a degree structure and
$(\mathcal {C}, \mathcal {C}_{F})$ is equipped with a degree structure and ![]() $\mathcal {C}$ is idempotent-complete. If
$\mathcal {C}$ is idempotent-complete. If ![]() $p_{*}$ preserves summand inclusions for some surjective morphism
$p_{*}$ preserves summand inclusions for some surjective morphism ![]() $p \colon y \to z$ in
$p \colon y \to z$ in ![]() $\mathcal {C}_{F}$, then for maps
$\mathcal {C}_{F}$, then for maps ![]() $x,x' \to y$ we can write
$x,x' \to y$ we can write
for some ![]() $c_{x,x'}$.
$c_{x,x'}$.
Proof. By assumption, we have decompositions
Since ![]() $\mathcal {C}$ is extensive, we can refine the first decomposition over the second, so that
$\mathcal {C}$ is extensive, we can refine the first decomposition over the second, so that
where
We claim that here ![]() $(p_{*}x)' \simeq \emptyset$. Once we have shown this, we are done since we then have
$(p_{*}x)' \simeq \emptyset$. Once we have shown this, we are done since we then have ![]() $p_{*}x \simeq (p_{*}x)_{d}$ and
$p_{*}x \simeq (p_{*}x)_{d}$ and ![]() $p_{*}x' \simeq c'$, so that
$p_{*}x' \simeq c'$, so that
By definition, ![]() $(p_{*}x)'$ fits in a pullback square
$(p_{*}x)'$ fits in a pullback square

Since the functor ![]() $p_{*}$ preserves pullbacks (being a right adjoint), we can identify the fibre product
$p_{*}$ preserves pullbacks (being a right adjoint), we can identify the fibre product ![]() $(p_{*}x)'$ with
$(p_{*}x)'$ with ![]() $p_{*}(x \times _{x \amalg x'} x') \simeq p_{*}(\emptyset )$. To identify
$p_{*}(x \times _{x \amalg x'} x') \simeq p_{*}(\emptyset )$. To identify ![]() $p_{*}(\emptyset )$, we first note that we have a counit map
$p_{*}(\emptyset )$, we first note that we have a counit map ![]() $p^{*}p_{*}(\emptyset ) \to \emptyset$, from which we conclude that
$p^{*}p_{*}(\emptyset ) \to \emptyset$, from which we conclude that ![]() $p^{*}p_{*}(\emptyset ) \simeq \emptyset$. On the other hand, by definition of
$p^{*}p_{*}(\emptyset ) \simeq \emptyset$. On the other hand, by definition of ![]() $p^{*}$ we have the cartesian square
$p^{*}$ we have the cartesian square

Since ![]() $p$ is by assumption surjective, so is the top horizontal map by Lemma 4.2.5(1), which implies
$p$ is by assumption surjective, so is the top horizontal map by Lemma 4.2.5(1), which implies ![]() $p_{*}(\emptyset ) \simeq \emptyset$ by Lemma 4.2.5(2).
$p_{*}(\emptyset ) \simeq \emptyset$ by Lemma 4.2.5(2).
Construction 4.2.14 Let ![]() $(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ be an extensive bispan triple, where
$(\mathcal {C},\mathcal {C}_{F},\mathcal {C}_{L})$ be an extensive bispan triple, where ![]() $(\mathcal {C}, \mathcal {C}_{F})$ is equipped with a degree structure and the
$(\mathcal {C}, \mathcal {C}_{F})$ is equipped with a degree structure and the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ is idempotent-complete. Fix a morphism
$\mathcal {C}$ is idempotent-complete. Fix a morphism ![]() $p\colon x \rightarrow y$ in
$p\colon x \rightarrow y$ in ![]() $\mathcal {C}_F$ such that
$\mathcal {C}_F$ such that ![]() $p_{*}$ preserves summand inclusions, and which is surjective in the sense of Definition 4.2.3. We then consider the following distributivity diagram for
$p_{*}$ preserves summand inclusions, and which is surjective in the sense of Definition 4.2.3. We then consider the following distributivity diagram for ![]() $x \amalg x \xrightarrow {\nabla _x} x \xrightarrow {p} y$ in the sense of Definition 2.4.1:
$x \amalg x \xrightarrow {\nabla _x} x \xrightarrow {p} y$ in the sense of Definition 2.4.1:

Note that, according to Remark 2.4.5, ![]() $w \rightarrow y$ is equivalent to
$w \rightarrow y$ is equivalent to ![]() $p_*(x \amalg x \rightarrow x)$. From Lemma 4.2.13 we then get a coproduct decomposition of
$p_*(x \amalg x \rightarrow x)$. From Lemma 4.2.13 we then get a coproduct decomposition of ![]() $w$ (over
$w$ (over ![]() $y$) as
$y$) as
Since coproduct decompositions are preserved under pullbacks, we get ![]() $p^*w \simeq x \amalg (c \times _y x) \amalg x$. Since coproducts are disjoint, we can further decompose the restriction of
$p^*w \simeq x \amalg (c \times _y x) \amalg x$. Since coproducts are disjoint, we can further decompose the restriction of ![]() $\epsilon$ to
$\epsilon$ to ![]() $c \times _y x \rightarrow x \amalg x$ as a coproduct of two morphisms:
$c \times _y x \rightarrow x \amalg x$ as a coproduct of two morphisms:
Restricting ![]() $\widetilde {p}$ to
$\widetilde {p}$ to ![]() $c_L$ and
$c_L$ and ![]() $c_R$ gives us two maps
$c_R$ gives us two maps
We also have the restriction of ![]() $g$ to
$g$ to ![]() $c$:
$c$:
All in all (
42) is equivalent to

We are particularly concerned with the following diagram, which we can extract from (43), where the middle square is cartesian:

The next lemma states that the maps ![]() $\widetilde {p}_L, \widetilde {p}_R$ defined above must be surjective. This will be used to prove polynomiality of
$\widetilde {p}_L, \widetilde {p}_R$ defined above must be surjective. This will be used to prove polynomiality of ![]() $p_{\otimes }$ via an inductive argument.
$p_{\otimes }$ via an inductive argument.
Lemma 4.2.15 Keeping the notation of Construction 4.2.14, we have ![]() $c_0^{(\widetilde {p}_i)} \simeq \emptyset$ for
$c_0^{(\widetilde {p}_i)} \simeq \emptyset$ for ![]() $i = L,R$.
$i = L,R$.
Proof. We prove the case ![]() $i = L$. To show that
$i = L$. To show that ![]() $\widetilde {p}_{L}$ has no component of degree
$\widetilde {p}_{L}$ has no component of degree ![]() $0$, let us decompose
$0$, let us decompose ![]() $c$ as
$c$ as
Then ![]() $p^{*}c_{0}^{(\widetilde {p}_{L})} \to p^{*}c \simeq c_{L} \amalg c_{R}$ factors through
$p^{*}c_{0}^{(\widetilde {p}_{L})} \to p^{*}c \simeq c_{L} \amalg c_{R}$ factors through ![]() $c_{R}$ (since, by definition, its component over
$c_{R}$ (since, by definition, its component over ![]() $c_{L}$ is
$c_{L}$ is ![]() $\emptyset$) and, hence, the composite
$\emptyset$) and, hence, the composite ![]() $p^{*}c_{0}^{(\widetilde {p}_{L})} \to x \amalg x$ factors through the right copy of
$p^{*}c_{0}^{(\widetilde {p}_{L})} \to x \amalg x$ factors through the right copy of ![]() $x$. But then the adjoint map
$x$. But then the adjoint map ![]() $c_{0}^{(\widetilde {p}_{L})} \to p_{*}(x \amalg x) \simeq y \amalg c \amalg y$ factors through the right copy of
$c_{0}^{(\widetilde {p}_{L})} \to p_{*}(x \amalg x) \simeq y \amalg c \amalg y$ factors through the right copy of ![]() $y$, which means
$y$, which means ![]() $c_{0}^{(\widetilde {p}_{L})} \simeq \emptyset$ since it also factors through
$c_{0}^{(\widetilde {p}_{L})} \simeq \emptyset$ since it also factors through ![]() $c$.
$c$.
For the remainder of this section, we fix an extensive bispan triple ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ such that:
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ such that:
•
 $\mathcal {C}$ is idempotent-complete;
$\mathcal {C}$ is idempotent-complete;•
 $(\mathcal {C}, \mathcal {C}_{F})$ has a degree structure;
$(\mathcal {C}, \mathcal {C}_{F})$ has a degree structure;•
 $p_{*}$ preserves summand inclusions for every surjective morphism
$p_{*}$ preserves summand inclusions for every surjective morphism  $p$ in
$p$ in  $\mathcal {C}_{F}$;
$\mathcal {C}_{F}$;
and an ![]() $L$-distributive functor
$L$-distributive functor ![]() $\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ such that
$\Phi \colon \operatorname {Span}_{F}(\mathcal {C}) \to {\text {Cat}}_\infty$ such that
(1)
 $\Phi$ preserves finite products and
$\Phi$ preserves finite products and(2) for each
 $x \in \mathcal {C}$, the
$x \in \mathcal {C}$, the  $\infty$-category
$\infty$-category  $\Phi (x)$ is additive.
$\Phi (x)$ is additive.
Remark 4.2.16 The assumption that ![]() $p_{*}$ preserves summand inclusions when
$p_{*}$ preserves summand inclusions when ![]() $p$ is surjective holds in all the examples from Example 4.2.6.
$p$ is surjective holds in all the examples from Example 4.2.6.
• In
 $(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$, if
$(\mathcal {S}, \mathcal {S}_{\mathrm {fin}})$, if  $p \colon Y \to Z$ is surjective with finite discrete fibres, then for
$p \colon Y \to Z$ is surjective with finite discrete fibres, then for  $X,X' \to Y$ we have
Since
$X,X' \to Y$ we have
Since \[ p_{*}(X_{0} \amalg X_{1})_{z} \simeq \prod_{y \in Y_{z}} (X_{0,z} \amalg X_{1,z}). \]
\[ p_{*}(X_{0} \amalg X_{1})_{z} \simeq \prod_{y \in Y_{z}} (X_{0,z} \amalg X_{1,z}). \]
 $p$ is surjective (so
$p$ is surjective (so  $Y_{z}\neq \emptyset$) and products in
$Y_{z}\neq \emptyset$) and products in  $\mathcal {S}$ preserve coproducts in each variable, we can write this as
$\mathcal {S}$ preserve coproducts in each variable, we can write this as  $\coprod _{\phi \colon Y_{z} \to \{0,1\}} \prod _{y \in Y_{z}} X_{\phi (y),z}$, where
$\coprod _{\phi \colon Y_{z} \to \{0,1\}} \prod _{y \in Y_{z}} X_{\phi (y),z}$, where  $\prod _{y \in Y_{z}} X_{0,z}$ splits off as a summand, naturally in
$\prod _{y \in Y_{z}} X_{0,z}$ splits off as a summand, naturally in  $z$.
$z$.• This argument also works in
 $\mathbb {F}$ and
$\mathbb {F}$ and  $\mathbb {F}_{G}$: to apply it in the latter case we can think of
$\mathbb {F}_{G}$: to apply it in the latter case we can think of  $\mathbb {F}_{G/Z}$ as
$\mathbb {F}_{G/Z}$ as  ${\text {Fun}}(\mathcal {Z}, \mathbb {F})$ where
${\text {Fun}}(\mathcal {Z}, \mathbb {F})$ where  $\mathcal {Z} \to BG$ is the unstraightening of
$\mathcal {Z} \to BG$ is the unstraightening of  $Z \colon BG \to \mathbb {F}$, and then interpret
$Z \colon BG \to \mathbb {F}$, and then interpret  $p_{*}$ as a right Kan extension along a map of groupoids with finite discrete fibres, which is then given fibrewise by a finite product.
$p_{*}$ as a right Kan extension along a map of groupoids with finite discrete fibres, which is then given fibrewise by a finite product.• In the algebro-geometric examples, we note that a summand inclusion corresponds to a clopen morphism of schemes (or, more generally, algebraic spaces; see Lemma 4.2.17), and the required condition then follows from the fact that Weil restriction along finite flat morphisms preserves both closed and open immersions [Reference RydhRyd11, Proposition 3.5(vi)–(vii)] and, thus, preserves summand inclusions.
Lemma 4.2.17 Let ![]() $j\colon X \rightarrow Y$ be a morphism of algebraic spaces. Then
$j\colon X \rightarrow Y$ be a morphism of algebraic spaces. Then ![]() $j$ is a summand inclusion if and only if
$j$ is a summand inclusion if and only if ![]() $j$ is a clopen immersion.
$j$ is a clopen immersion.
Proof. We freely use the fact that the result holds if we replace ‘algebraic spaces’ with ‘schemes’ which, in turn, follows from the fact that direct sum decomposition of schemes is computed on the level of underlying topological spaces. The ‘only if’ direction follows from [Sta, Tag 02WN]. Suppose that ![]() $j$ is an clopen immersion. Choose a presentation of
$j$ is an clopen immersion. Choose a presentation of ![]() $Y$ as a quotient
$Y$ as a quotient ![]() $U/R$ where
$U/R$ where ![]() $q:U \rightarrow Y$ is surjective étale morphism and
$q:U \rightarrow Y$ is surjective étale morphism and ![]() $s, t\colon R \rightarrow U$ is an equivalence relation. The pullback of
$s, t\colon R \rightarrow U$ is an equivalence relation. The pullback of ![]() $j$ along
$j$ along ![]() $q\colon U \rightarrow Y$ then defines a clopen immersion of schemes
$q\colon U \rightarrow Y$ then defines a clopen immersion of schemes ![]() $j'\colon U' :=q^{-1}(X) \hookrightarrow U$; similarly we get a clopen immersion of schemes
$j'\colon U' :=q^{-1}(X) \hookrightarrow U$; similarly we get a clopen immersion of schemes ![]() $R':=s^{-1}(U') \simeq t^{-1}(U') \hookrightarrow R$. Now, using the corresponding result for schemes, we set the complement of
$R':=s^{-1}(U') \simeq t^{-1}(U') \hookrightarrow R$. Now, using the corresponding result for schemes, we set the complement of ![]() $U'$ in
$U'$ in ![]() $U$ to be
$U$ to be ![]() $U''$, which comes equipped with a clopen immersion
$U''$, which comes equipped with a clopen immersion ![]() $U'' \hookrightarrow U$. Furthermore, note that the complement of
$U'' \hookrightarrow U$. Furthermore, note that the complement of ![]() $R'$ in
$R'$ in ![]() $R$ also defines an equivalence relation
$R$ also defines an equivalence relation ![]() $R''$ on
$R''$ on ![]() $X$ (this can be checked on test schemes, whence the result follows from the corresponding result on the level of sets) such that the two maps
$X$ (this can be checked on test schemes, whence the result follows from the corresponding result on the level of sets) such that the two maps ![]() $R'' \hookrightarrow R \xrightarrow {s,t} X$ factor through
$R'' \hookrightarrow R \xrightarrow {s,t} X$ factor through ![]() $U''$ as
$U''$ as ![]() $s'',t'':R'' \rightarrow U''$. We then take the quotient
$s'',t'':R'' \rightarrow U''$. We then take the quotient ![]() $X':= U''/R''$, which exists as an algebraic space. Since coequalizers and coproducts commute, we have a decomposition
$X':= U''/R''$, which exists as an algebraic space. Since coequalizers and coproducts commute, we have a decomposition ![]() $Y \simeq X \coprod X'$.
$Y \simeq X \coprod X'$.
The following computation follows [Reference Bachmann and HoyoisBH21, Corollary 5.15] closely.
Lemma 4.2.18 For any ![]() $p \colon x \rightarrow y$ in
$p \colon x \rightarrow y$ in ![]() $\mathcal {C}_F$, we have for any
$\mathcal {C}_F$, we have for any ![]() $E, F \in \Phi (x)$ an equivalence
$E, F \in \Phi (x)$ an equivalence
in terms of (43).
Proof. The distributivity transformation (Definition 2.4.9) for (42) gives an equivalence
The claim then follows from this equivalence, the transitivity of all the functors involved, and the identification of ![]() $\nabla _{\oplus }$ with the direct sum functor, which follows from the assumption that
$\nabla _{\oplus }$ with the direct sum functor, which follows from the assumption that ![]() $F$ is product-preserving.
$F$ is product-preserving.
Remark 4.2.19 For any morphism ![]() $\phi \colon y \to x$ in
$\phi \colon y \to x$ in ![]() $\mathcal {C}_{L}$, it is easy to see that the diagram
$\mathcal {C}_{L}$, it is easy to see that the diagram

is a distributivity diagram since for ![]() $\alpha \colon z \to x$ we have an equivalence
$\alpha \colon z \to x$ we have an equivalence

It follows that for our ![]() $L$-distributive functor
$L$-distributive functor ![]() $\Phi$ we have an equivalence
$\Phi$ we have an equivalence
of functors ![]() $\Phi (y)\times \Phi (x) \to \Phi (x)$. If we take
$\Phi (y)\times \Phi (x) \to \Phi (x)$. If we take ![]() $\phi = \nabla _{x}$, then
$\phi = \nabla _{x}$, then ![]() $\nabla _{x}^{\circledast }$ is the diagonal
$\nabla _{x}^{\circledast }$ is the diagonal ![]() $\Phi (x) \to \Phi (x) \times \Phi (x)$ (since
$\Phi (x) \to \Phi (x) \times \Phi (x)$ (since ![]() $\Phi$ by assumption preserves products) and, hence, its left adjoint
$\Phi$ by assumption preserves products) and, hence, its left adjoint ![]() $\nabla _{x,\oplus }$ is the coproduct on
$\nabla _{x,\oplus }$ is the coproduct on ![]() $\Phi (x)$. From this the previous equivalence specializes for
$\Phi (x)$. From this the previous equivalence specializes for ![]() $E,E',F \in \Phi (x)$ to a natural equivalence
$E,E',F \in \Phi (x)$ to a natural equivalence
so that the functor ![]() $\nabla _{x,\otimes }$ preserves coproducts in each variable.
$\nabla _{x,\otimes }$ preserves coproducts in each variable.
Proposition 4.2.20 Suppose ![]() $p \colon x \rightarrow y$ is a morphism of degree
$p \colon x \rightarrow y$ is a morphism of degree ![]() $\leq n$ in
$\leq n$ in ![]() $\mathcal {C}_F$ (for
$\mathcal {C}_F$ (for ![]() $n \geq -1$). Then the functor
$n \geq -1$). Then the functor ![]() $p_{\otimes } \colon \Phi (x) \to \Phi (y)$ is polynomial of degree
$p_{\otimes } \colon \Phi (x) \to \Phi (y)$ is polynomial of degree ![]() $\leq n$.
$\leq n$.
Proof. By convention, a degree-![]() $(-1)$ morphism is given by
$(-1)$ morphism is given by ![]() $\emptyset \rightarrow \emptyset$ and, thus, defines the zero functor, a polynomial functor of degree
$\emptyset \rightarrow \emptyset$ and, thus, defines the zero functor, a polynomial functor of degree ![]() $-1$. We now proceed by induction. Since any morphism
$-1$. We now proceed by induction. Since any morphism ![]() $\emptyset \rightarrow y$ of degree 0 induces a constant functor
$\emptyset \rightarrow y$ of degree 0 induces a constant functor ![]() $\Phi (\emptyset ) \simeq \ast \rightarrow \Phi (y)$, a degree-0 morphism gives a polynomial functor of degree
$\Phi (\emptyset ) \simeq \ast \rightarrow \Phi (y)$, a degree-0 morphism gives a polynomial functor of degree ![]() $\leq 0$. Now let us assume that the result has been proved for any morphism of degree
$\leq 0$. Now let us assume that the result has been proved for any morphism of degree ![]() $\leq n-1$ for
$\leq n-1$ for ![]() $n \geq 1$. Consider the diagram (43). Since degree-
$n \geq 1$. Consider the diagram (43). Since degree-![]() $n$ morphisms are stable under pullback, the morphism
$n$ morphisms are stable under pullback, the morphism ![]() $\widetilde {p}_L \amalg \widetilde {p}_R \colon c_L \amalg c_R \rightarrow c$ is also of degree
$\widetilde {p}_L \amalg \widetilde {p}_R \colon c_L \amalg c_R \rightarrow c$ is also of degree ![]() $n$. Since
$n$. Since ![]() $\Phi$ preserves coproduct decompositions in
$\Phi$ preserves coproduct decompositions in ![]() $\mathcal {C}$ (which are the products in bispans) by assumption, coproducts of polynomials of degree
$\mathcal {C}$ (which are the products in bispans) by assumption, coproducts of polynomials of degree ![]() $\leq n$ are likewise polynomial of degree
$\leq n$ are likewise polynomial of degree ![]() $\leq n$ by Proposition 4.1.5. Since we already proved the case of degree
$\leq n$ by Proposition 4.1.5. Since we already proved the case of degree ![]() $0$, we may assume that
$0$, we may assume that ![]() $y^{(p)}_0 \simeq \emptyset$ and, hence, apply Construction 4.2.14.
$y^{(p)}_0 \simeq \emptyset$ and, hence, apply Construction 4.2.14.
Now, ![]() $c_L \amalg c_R \rightarrow c$ is the composite
$c_L \amalg c_R \rightarrow c$ is the composite
We claim that here ![]() $\widetilde {p}_L$ and
$\widetilde {p}_L$ and ![]() $\widetilde {p}_R$ are both of degree
$\widetilde {p}_R$ are both of degree ![]() $\leq n-1$: indeed, since both maps have no component of degree
$\leq n-1$: indeed, since both maps have no component of degree ![]() $0$ it follows from the description of the degree decomposition of (45) in Construction 4.2.8 and the additivity condition (4) in (4.2.3) that a component of degree
$0$ it follows from the description of the degree decomposition of (45) in Construction 4.2.8 and the additivity condition (4) in (4.2.3) that a component of degree ![]() $\geq n$ in either map would produce a component of degree
$\geq n$ in either map would produce a component of degree ![]() $> n$ in (45), which is impossible.
$> n$ in (45), which is impossible.
Hence, by the inductive hypothesis ![]() $(\widetilde {p}_L)_{\otimes }$ and
$(\widetilde {p}_L)_{\otimes }$ and ![]() $(\widetilde {p}_R)_{\otimes }$ are polynomial functors of degree
$(\widetilde {p}_R)_{\otimes }$ are polynomial functors of degree ![]() $\leq n-1$. To conclude, we fix
$\leq n-1$. To conclude, we fix ![]() $E$ and note that Lemma 4.2.18 yields an equivalence:
$E$ and note that Lemma 4.2.18 yields an equivalence:
Here ![]() $\nabla _{c,\otimes }(X,-)$ preserves finite coproducts by Remark 4.2.19, as does
$\nabla _{c,\otimes }(X,-)$ preserves finite coproducts by Remark 4.2.19, as does ![]() $k_{\oplus }$ since it is a left adjoint, so the composite
$k_{\oplus }$ since it is a left adjoint, so the composite ![]() $k_{\oplus }\nabla _{c,\otimes }\big (\widetilde {p}_{L,\otimes }\epsilon _L^{\circledast }(E),\widetilde {p}_{R,\otimes }\epsilon _R^{\circledast }(-)\big )$ is polynomial of degree
$k_{\oplus }\nabla _{c,\otimes }\big (\widetilde {p}_{L,\otimes }\epsilon _L^{\circledast }(E),\widetilde {p}_{R,\otimes }\epsilon _R^{\circledast }(-)\big )$ is polynomial of degree ![]() $\leq n-1$ by [Reference Bachmann and HoyoisBH21, Lemma 5.24(4)]. Using Proposition 4.1.5 again we get that
$\leq n-1$ by [Reference Bachmann and HoyoisBH21, Lemma 5.24(4)]. Using Proposition 4.1.5 again we get that ![]() $D_E(p_{\otimes })(-)$ is polynomial of degree
$D_E(p_{\otimes })(-)$ is polynomial of degree ![]() $\leq n-1$ and, hence,
$\leq n-1$ and, hence, ![]() $p_{\otimes }$ is polynomial of degree
$p_{\otimes }$ is polynomial of degree ![]() $\leq n$.
$\leq n$.
Since any morphism in ![]() $\mathcal {C}_{F}$ has a degree decomposition consisting of finitely many terms and so is of degree
$\mathcal {C}_{F}$ has a degree decomposition consisting of finitely many terms and so is of degree ![]() $\leq n$ for some
$\leq n$ for some ![]() $n$, we have shown the following.
$n$, we have shown the following.
Corollary 4.2.21 Let ![]() $p \colon x \rightarrow y$ be a morphism in
$p \colon x \rightarrow y$ be a morphism in ![]() $\mathcal {C}_F$. Then
$\mathcal {C}_F$. Then ![]() $p_{\otimes }$ is a polynomial functor.
$p_{\otimes }$ is a polynomial functor.
Example 4.2.22 Corollary 4.2.21 applies, for instance, for any finite group ![]() $G$ to the bispan triple
$G$ to the bispan triple ![]() $(\mathbb {F}_{G},\mathbb {F}_{G},\mathbb {F}_{G})$ of finite
$(\mathbb {F}_{G},\mathbb {F}_{G},\mathbb {F}_{G})$ of finite ![]() $G$-sets and the
$G$-sets and the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category of
$\infty$-category of ![]() $G$-spectra as discussed in Proposition 3.4.19. In this case we can conclude, in particular, that for any subgroup inclusion
$G$-spectra as discussed in Proposition 3.4.19. In this case we can conclude, in particular, that for any subgroup inclusion ![]() $H \subseteq G$, the Hill–Hopkins–Ravenel norm
$H \subseteq G$, the Hill–Hopkins–Ravenel norm ![]() ${\text {Sp}}^{H} \to {\text {Sp}}^{G}$ is a polynomial functor. This example has already been studied in more detail by Konovalov [Reference KonovalovKon20], though the proof of polynomiality is similar to ours.
${\text {Sp}}^{H} \to {\text {Sp}}^{G}$ is a polynomial functor. This example has already been studied in more detail by Konovalov [Reference KonovalovKon20], though the proof of polynomiality is similar to ours.
4.3 From bispans to Tambara functors
Summarizing the results of the previous two subsections, we have shown the following.
Corollary 4.3.1 Let ![]() $(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ be an extensive bispan triple such that
$(\mathcal {C}, \mathcal {C}_{F}, \mathcal {C}_{L})$ be an extensive bispan triple such that ![]() $\mathcal {C}$ is idempotent-complete and
$\mathcal {C}$ is idempotent-complete and ![]() $(\mathcal {C}, \mathcal {C}_{F})$ has a degree structure. Assume, moreover, that
$(\mathcal {C}, \mathcal {C}_{F})$ has a degree structure. Assume, moreover, that ![]() $p_{*}$ preserves summand inclusions for every surjective morphism
$p_{*}$ preserves summand inclusions for every surjective morphism ![]() $p$ in
$p$ in ![]() $\mathcal {C}_{F}$, and suppose that
$\mathcal {C}_{F}$, and suppose that ![]() $\Phi \colon \operatorname {Span}_{F} \to {\text {Cat}}_\infty$ is an
$\Phi \colon \operatorname {Span}_{F} \to {\text {Cat}}_\infty$ is an ![]() $L$-distributive functor such that:
$L$-distributive functor such that:
•
 $\Phi$ preserves finite products;
$\Phi$ preserves finite products;• for each
 $x \in \mathcal {C}$, the
$x \in \mathcal {C}$, the  $\infty$-category
$\infty$-category  $\Phi (x)$ is stable and idempotent-complete;
$\Phi (x)$ is stable and idempotent-complete;• for each morphism
 $f \colon x \to y$ in
$f \colon x \to y$ in  $\mathcal {C}$, the functor
$\mathcal {C}$, the functor  $f^{\circledast } \colon \Phi (x) \to \Phi (y)$ is polynomial.Footnote 17
$f^{\circledast } \colon \Phi (x) \to \Phi (y)$ is polynomial.Footnote 17
Then ![]() $\Phi$ extends to a functor
$\Phi$ extends to a functor ![]() $\widetilde {\Phi } \colon {\text {Bispan}}_{F,L}(\mathcal {C}) \to {\text {Cat}}_\infty ^{\mathrm {poly}}$ and, hence, induces a product-preserving functor
$\widetilde {\Phi } \colon {\text {Bispan}}_{F,L}(\mathcal {C}) \to {\text {Cat}}_\infty ^{\mathrm {poly}}$ and, hence, induces a product-preserving functor ![]() ${\text {Bispan}}_{F,L}(\mathcal {C}) \to \mathcal {S}$ given on an object
${\text {Bispan}}_{F,L}(\mathcal {C}) \to \mathcal {S}$ given on an object ![]() $x \in \mathcal {C}$ by
$x \in \mathcal {C}$ by ![]() $\Omega ^{\infty }K(\Phi (x))$.
$\Omega ^{\infty }K(\Phi (x))$.
Our goal in this final subsection is to give some applications of this result towards obtaining new structure on algebraic ![]() $K$-theory.
$K$-theory.
We first consider the equivariant situation, as previously discussed in § 3.4. For a finite group ![]() $G$ the category
$G$ the category ![]() $\mathbb {F}_{G}$ of finite
$\mathbb {F}_{G}$ of finite ![]() $G$-sets is extensive and idempotent-complete, and by Example 4.2.6(3) it also has a degree structure. We therefore get the following.
$G$-sets is extensive and idempotent-complete, and by Example 4.2.6(3) it also has a degree structure. We therefore get the following.
Corollary 4.3.2 Let ![]() $\mathcal {C} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ be a
$\mathcal {C} \colon \operatorname {Span}(\mathbb {F}_{G}) \to {\text {Cat}}_\infty$ be a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category that is compatible with additive transfers. If the
$\infty$-category that is compatible with additive transfers. If the ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}^{H}$ is stable and idempotent-complete for every
$\mathcal {C}^{H}$ is stable and idempotent-complete for every ![]() $H \subseteq G$, then
$H \subseteq G$, then ![]() $\mathcal {C}$ extends to a functor
$\mathcal {C}$ extends to a functor
and, hence, induces a product-preserving functor
Remark 4.3.3 A Tambara functor [Reference TambaraTam93] is a functor ![]() $T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Ab}}$, or equivalently a functor
$T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Ab}}$, or equivalently a functor ![]() $T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Set}}$ such that the induced commutative monoid structure on
$T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to {\text {Set}}$ such that the induced commutative monoid structure on ![]() $T(G/H)$ is a group for every
$T(G/H)$ is a group for every ![]() $H \subseteq G$. The output of Corollary 4.3.2 is an
$H \subseteq G$. The output of Corollary 4.3.2 is an ![]() $\infty$-categorical analogue of this: it is a functor
$\infty$-categorical analogue of this: it is a functor ![]() $T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$ such that the commutative monoid structure on
$T \colon {\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$ such that the commutative monoid structure on ![]() $T(G/H)$ is grouplike for every
$T(G/H)$ is grouplike for every ![]() $H \subseteq G$. We will refer to this as a homotopical Tambara functor. Note that it is expected that connective genuine
$H \subseteq G$. We will refer to this as a homotopical Tambara functor. Note that it is expected that connective genuine ![]() $G$-
$G$-![]() $E_{\infty }$-ring spectra are equivalent to these homotopical Tambara functors.
$E_{\infty }$-ring spectra are equivalent to these homotopical Tambara functors.
Example 4.3.4 By Proposition 3.4.19 the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category of
$\infty$-category of ![]() $G$-spectra (given by
$G$-spectra (given by ![]() $G/H \mapsto {\text {Sp}}^{H}$) satisfies the hypotheses of Corollary 4.3.2. Hence, the
$G/H \mapsto {\text {Sp}}^{H}$) satisfies the hypotheses of Corollary 4.3.2. Hence, the ![]() $G$-equivariant
$G$-equivariant ![]() $K$-theory of the sphere spectrum is a homotopical Tambara functor: the functor
$K$-theory of the sphere spectrum is a homotopical Tambara functor: the functor
extends canonically to a product-preserving functor ![]() ${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}.$
${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}.$
To generalize this, we introduce some terminology.
Definition 4.3.5 Let ![]() $G$ be a finite group. For us a genuine
$G$ be a finite group. For us a genuine ![]() $G$-
$G$- ![]() $\mathbb {E}_{\infty }$-ring spectrum
$\mathbb {E}_{\infty }$-ring spectrum ![]() $E$ will be a section of the cocartesian fibration
$E$ will be a section of the cocartesian fibration ![]() $\int {\text {Sp}}_G \rightarrow \operatorname {Span}(\mathbb {F}_G)$ sending a backward arrow to a cocartesian edge.
$\int {\text {Sp}}_G \rightarrow \operatorname {Span}(\mathbb {F}_G)$ sending a backward arrow to a cocartesian edge.
Remark 4.3.6 This definition mimics the definition of a normed motivic spectrum in the context of motivic homotopy theory [Reference Bachmann and HoyoisBH21]; see especially [Reference Bachmann and HoyoisBH21, Definition 9.14]. As explained there, it is also equivalent to the classical definition of a genuine ![]() $G$-
$G$-![]() $\mathbb {E}_{\infty }$-ring spectrum by comparison of associated monads.
$\mathbb {E}_{\infty }$-ring spectrum by comparison of associated monads.
By a similar argument as in [Reference Bachmann and HoyoisBH21, Proposition 7.6(4)], the formation of modules assemble into a functor
which satisfies the hypotheses of Corollary 4.3.2. We then have the following theorem.
Theorem 4.3.7 The algebraic ![]() $K$-theory of a genuine
$K$-theory of a genuine ![]() $G$-
$G$-![]() $\mathbb {E}_{\infty }$-ring spectrum
$\mathbb {E}_{\infty }$-ring spectrum ![]() $E$ is a homotopical Tambara functor: the functor
$E$ is a homotopical Tambara functor: the functor
extends canonically to a product-preserving functor ![]() ${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}.$
${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}.$
Remark 4.3.8 As already mentioned, a homotopical Tambara functor is expected to be the same thing as a connective ![]() $G$-
$G$-![]() $\mathbb {E}_{\infty }$-ring spectrum. Assuming this, Theorem 4.3.7 says that algebraic
$\mathbb {E}_{\infty }$-ring spectrum. Assuming this, Theorem 4.3.7 says that algebraic ![]() $K$-theory preserves
$K$-theory preserves ![]() $G$-
$G$-![]() $\mathbb {E}_{\infty }$-ring structures. As far as we are aware, this is a completely new structure on algebraic
$\mathbb {E}_{\infty }$-ring structures. As far as we are aware, this is a completely new structure on algebraic ![]() $K$-theory. Indeed, the recent paper [Reference Guillou, May, Merling and OsornoGMMO23] seems to be the first to construct even an associative ring structure valued in
$K$-theory. Indeed, the recent paper [Reference Guillou, May, Merling and OsornoGMMO23] seems to be the first to construct even an associative ring structure valued in ![]() $G$-spectra, though the results of [Reference Barwick, Glasman and ShahBGS20] should also suffice to construct
$G$-spectra, though the results of [Reference Barwick, Glasman and ShahBGS20] should also suffice to construct ![]() $K(E)$ as an ordinary
$K(E)$ as an ordinary ![]() $E_{\infty }$-algebra in
$E_{\infty }$-algebra in ![]() $G$-spectra.
$G$-spectra.
Another interesting class of examples arises from the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories obtained from group actions as in Example 3.4.17.
$\infty$-categories obtained from group actions as in Example 3.4.17.
Corollary 4.3.9 Let ![]() $\mathcal {C}$ be an idempotent-complete small stable
$\mathcal {C}$ be an idempotent-complete small stable ![]() $\infty$-category, equipped with a symmetric monoidal structure that is compatible with finite coproducts. Then the functor
$\infty$-category, equipped with a symmetric monoidal structure that is compatible with finite coproducts. Then the functor
extends canonically to a homotopical Tambara functor ![]() ${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}$.
${\text {Bispan}}(\mathbb {F}_G) \rightarrow \mathcal {S}$.
Remark 4.3.10 In [Reference Barwick, Glasman and ShahBGS20], the authors proved that the ![]() $K$-theory of a ‘naïve’
$K$-theory of a ‘naïve’ ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category admits the structure of a Green functor. The previous corollary treats the case of a
$\infty$-category admits the structure of a Green functor. The previous corollary treats the case of a ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category where the action is trivial and produces a Tambara functor. We expect that a more general statement holds: the
$\infty$-category where the action is trivial and produces a Tambara functor. We expect that a more general statement holds: the ![]() $K$-theory of certain ‘naïve’
$K$-theory of certain ‘naïve’ ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-categories should also form Tambara functors. We leave this to the interested reader.
$\infty$-categories should also form Tambara functors. We leave this to the interested reader.
Example 4.3.11 As in Example 3.4.18, let ![]() $R$ be an
$R$ be an ![]() $\mathbb {E}_{\infty }$-ring spectrum and consider the
$\mathbb {E}_{\infty }$-ring spectrum and consider the ![]() $G$-symmetric monoidal
$G$-symmetric monoidal ![]() $\infty$-category from that example, given by
$\infty$-category from that example, given by ![]() $G/H \mapsto {\text {Fun}}(BG, \mathrm {Perf}(R))$. We obtain a homotopical Tambara functor
$G/H \mapsto {\text {Fun}}(BG, \mathrm {Perf}(R))$. We obtain a homotopical Tambara functor ![]() ${\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$ given by
${\text {Bispan}}(\mathbb {F}_{G}) \to \mathcal {S}$ given by
Lastly, we note that plugging in our algebro-geometric examples of bispans also gives additional structure on ![]() $K$-theory. Applying Corollary 4.3.1 to the extension of
$K$-theory. Applying Corollary 4.3.1 to the extension of ![]() $\mathrm {Perf}$ to bispans as in Theorem 3.6.8 gives us the following result about the
$\mathrm {Perf}$ to bispans as in Theorem 3.6.8 gives us the following result about the ![]() $K$-theory of spectral Deligne–Mumford stacks.
$K$-theory of spectral Deligne–Mumford stacks.
Theorem 4.3.12 The ![]() $K$-theory presheaf
$K$-theory presheaf
canonically extends to a product-preserving functor ![]() ${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},{\mathcal {FP}'}(\mathrm {SpDM}_{S}) \rightarrow \mathcal {S}$.
${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},{\mathcal {FP}'}(\mathrm {SpDM}_{S}) \rightarrow \mathcal {S}$.
In other words, the ![]() $K$-theory of spectral Deligne–Mumford stacks has multiplicative norms along finite étale maps. On the other hand, applying Theorem 3.5.9 gives us a result about the
$K$-theory of spectral Deligne–Mumford stacks has multiplicative norms along finite étale maps. On the other hand, applying Theorem 3.5.9 gives us a result about the ![]() $K$-theory of
$K$-theory of ![]() $\mathrm {SH}$, which is in some sense a stable analogue of the secondary
$\mathrm {SH}$, which is in some sense a stable analogue of the secondary ![]() $K$-theory explored in the thesis of Röndigs [Reference RöndigsRön16].
$K$-theory explored in the thesis of Röndigs [Reference RöndigsRön16].
Theorem 4.3.13 The ![]() $K$-theory presheaf
$K$-theory presheaf
canonically extends to a product-preserving functor ![]() ${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},{\mathrm {sm}}(\mathrm {AlgSpc}_{S}) \rightarrow \mathcal {S}$.
${\text {Bispan}}_{\text {f} {\unicode{x00E8}} \text{t}},{\mathrm {sm}}(\mathrm {AlgSpc}_{S}) \rightarrow \mathcal {S}$.
Remark 4.3.14 The multiplicative pushforwards along finite étale morphisms on ![]() $\mathrm {SH}$ induce a kind of ‘Adams operations’ on
$\mathrm {SH}$ induce a kind of ‘Adams operations’ on ![]() $K(\mathrm {SH})$. It would be interesting to explore some computational consequences of this structure.
$K(\mathrm {SH})$. It would be interesting to explore some computational consequences of this structure.
Acknowledgements
We would like to thank Clark Barwick for his influence in thinking about things in terms of spans, Andrew Macpherson and Irakli Patchkoria for helpful discussions, Marc Hoyois for some corrections on an earlier draft and help with formulating the correct version of Construction 4.2.14, and the Gorilla Brewery of Busan for providing the setting for the initial inspiration for this paper. We also thank the anonymous referee for suggesting a much simpler approach to our main result, by reducing it to the universal property for spans.
Much of this paper was written while the second author was employed by the IBS Center for Geometry and Physics in a position funded by the grant IBS-R003-D1 of the Institute for Basic Science, Republic of Korea. This project has also received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 101001474) and from the Research Council of Norway (project no. 313472, ‘Equations in motivic homotopy’).
Conflicts of Interest
None.