Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T22:43:57.837Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical criteria for divisors on 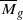to be ample

Part of: Curves Birational geometry

Published online by Cambridge University Press:  04 September 2009

Angela Gibney
Angela Gibney*
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, USA (email: agibney@math.uga.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The moduli space 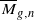of n-pointed stable curves of genus g is stratified by the topological type of the curves being parameterized: the closure of the locus of curves with k nodes has codimension k. The one-dimensional components of this stratification are smooth rational curves called F-curves. These are believed to determine all ample divisors. F-conjecture 

A divisor on 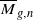 is ample if and only if it positively intersects theF-curves.

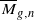In this paper, proving the F-conjecture on is reduced to showing that certain divisors on 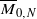for N⩽g+n are equivalent to the sum of the canonical divisor plus an effective divisor supported on the boundary. Numerical criteria and an algorithm are given to check whether a divisor is ample. By using a computer program called the Nef Wizard, written by Daniel Krashen, one can verify the conjecture for low genus. This is done on 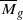for g⩽24, more than doubling the number of cases for which the conjecture is known to hold and showing that it is true for the first genera such that 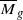is known to be of general type.

MSC classification

Secondary: 14H10: Families, moduli (algebraic) 14E30: Minimal model program (Mori theory, extremal rays)
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 5 , September 2009 , pp. 1227 - 1248
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Arbarello, E. and Cornalba, M., Calculating cohomology groups of moduli spaces of curves via algebraic geometry, Publ. Math. Inst. Hautes Études Sci. 88 (1998), 97–127.Google Scholar
[2]Avis, D. and Fukuda, K., lrslib version 4.1 (2001), http://cgm.cs.mcgill.ca/∼avis/C/lrs.html; lrslib is an ANSI C implementation of the reverse search algorithm for vertex enumeration/convex hull problems.Google Scholar
[3]Farkas, G., The geometry of the moduli space of curves of genus 23, Math. Ann. 318 (2000), 43–65.Google Scholar
[4]Farkas, G., Syzygies of curves and the effective cone of , Duke Math. J. 135 (2006), 53–98.CrossRefGoogle Scholar
[5]Farkas, G. and Gibney, A., The mori cones of moduli spaces of pointed curves of small genus, Trans. Amer. Math. Soc. 355 (2003), 1183–1199.CrossRefGoogle Scholar
[6]Gibney, A., Fibrations of , PhD thesis, University of Texas at Austin (2000).Google Scholar
[7]Gibney, A., Keel, S. and Morrison, I., Towards the ample cone of , J. Amer. Math. Soc. (2) 15 (2001), 273–294.Google Scholar
[8]Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).Google Scholar
[9]Keel, S. and McKernan, J., Contractible extremal rays of , Preprint (1996), arXiv:math.AG/9607009.Google Scholar
[10]Kollár, J., Rational curves on algebraic varieties (Springer, Berlin, 1991).Google Scholar
[11]Rulla, W., The birational geometry of  and , PhD thesis, University of Texas at Austin (2001), http://www.math.uga.edu/∼rulla/.Google Scholar