Article contents
Level-raising for Saito–Kurokawa forms
Published online by Cambridge University Press: 01 July 2009
Abstract
This paper provides congruences between unstable and stable automorphic forms for the symplectic similitude group GSp(4). More precisely, we raise the level of certain CAP representations Π arising from classical modular forms. We first transfer Π to π on a suitable inner form G; this is achieved by θ-lifting. For π, we prove a precise level-raising result that is inspired by the work of Bellaiche and Clozel and which relies on computations of Schmidt. We thus obtain a 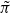 congruent to π, with a local component that is irreducibly induced from an unramified twist of the Steinberg representation of the Klingen parabolic. To transfer
congruent to π, with a local component that is irreducibly induced from an unramified twist of the Steinberg representation of the Klingen parabolic. To transfer 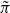 back to GSp(4), we use Arthur’s stable trace formula. Since
back to GSp(4), we use Arthur’s stable trace formula. Since 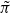 has a local component of the above type, all endoscopic error terms vanish. Indeed, by results due to Weissauer, we only need to show that such a component does not participate in the θ-correspondence with any GO(4); this is an exercise in using Kudla’s filtration of the Jacquet modules of the Weil representation. We therefore obtain a cuspidal automorphic representation
has a local component of the above type, all endoscopic error terms vanish. Indeed, by results due to Weissauer, we only need to show that such a component does not participate in the θ-correspondence with any GO(4); this is an exercise in using Kudla’s filtration of the Jacquet modules of the Weil representation. We therefore obtain a cuspidal automorphic representation 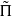 of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for
of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for 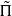 to have vectors fixed by the non-special maximal compact subgroups at all primes dividing N. Since G is necessarily ramified at some prime r, we have to show a non-special analogue of the fundamental lemma at r. Finally, we give an application of our main result to the Bloch–Kato conjecture, assuming a conjecture of Skinner and Urban on the rank of the monodromy operators at the primes dividing N.
to have vectors fixed by the non-special maximal compact subgroups at all primes dividing N. Since G is necessarily ramified at some prime r, we have to show a non-special analogue of the fundamental lemma at r. Finally, we give an application of our main result to the Bloch–Kato conjecture, assuming a conjecture of Skinner and Urban on the rank of the monodromy operators at the primes dividing N.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2009
References
- 3
- Cited by




