Introduction
For simplicity, let us work over a field
![]() $k$
. (Later,
$k$
. (Later,
![]() $k$
will be replaced by a noetherian ring
$k$
will be replaced by a noetherian ring
![]() $R$
.)
$R$
.)
Let
![]() $\mathfrak{M}$
be an abelian
$\mathfrak{M}$
be an abelian
![]() $k$
-linear algebraic stack. Roughly, this means that
$k$
-linear algebraic stack. Roughly, this means that
![]() $\mathfrak{M}$
is at the same time a
$\mathfrak{M}$
is at the same time a
![]() $k$
-linear abelian category with finite-dimensional hom-spaces, and an algebraic stack, locally of finite type over
$k$
-linear abelian category with finite-dimensional hom-spaces, and an algebraic stack, locally of finite type over
![]() $k$
. (The precise definition of linear algebraic stack is Definition 1.9. In the body of the paper we work with exact, instead of abelian, categories; see the beginning of § 3.)
$k$
. (The precise definition of linear algebraic stack is Definition 1.9. In the body of the paper we work with exact, instead of abelian, categories; see the beginning of § 3.)
Examples we are interested in include:
(i)
 $\mathfrak{M}=\mathfrak{Coh}_{Y}$
, the moduli stack of coherent
$\mathfrak{M}=\mathfrak{Coh}_{Y}$
, the moduli stack of coherent
 $\mathscr{O}_{Y}$
-modules, for a projective
$\mathscr{O}_{Y}$
-modules, for a projective
 $k$
-variety
$k$
-variety
 $Y$
;
$Y$
;(ii)
 $\mathfrak{M}=\mathfrak{Rep}_{Q}$
, the moduli stack of representations of a quiver
$\mathfrak{M}=\mathfrak{Rep}_{Q}$
, the moduli stack of representations of a quiver
 $Q$
on finite-dimensional
$Q$
on finite-dimensional
 $k$
-vector spaces;
$k$
-vector spaces;(iii) (the case
 $Y=Q=\operatorname{Spec}k$
)
$Y=Q=\operatorname{Spec}k$
)
 $\mathfrak{M}=\mathfrak{Vect}$
, the stack of finite-dimensional
$\mathfrak{M}=\mathfrak{Vect}$
, the stack of finite-dimensional
 $k$
-vector spaces. In this case,
$k$
-vector spaces. In this case,
 $\mathfrak{Vect}(S)$
, for a
$\mathfrak{Vect}(S)$
, for a
 $k$
-scheme
$k$
-scheme
 $S$
, is the exact
$S$
, is the exact
 $\mathscr{O}(S)$
-linear category of vector bundles over
$\mathscr{O}(S)$
-linear category of vector bundles over
 $S$
, and
$S$
, and
 $\mathfrak{Vect}(k)$
is the abelian
$\mathfrak{Vect}(k)$
is the abelian
 $k$
-linear category of finite-dimensional
$k$
-linear category of finite-dimensional
 $k$
-vector spaces. As an algebraic stack,
$k$
-vector spaces. As an algebraic stack,
 $\mathfrak{Vect}$
is
$\mathfrak{Vect}$
is  $$\begin{eqnarray}\mathfrak{Vect}=\operatorname{Spec}k\amalg B\operatorname{GL}_{1}\amalg B\operatorname{GL}_{2}\amalg \ldots .\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{Vect}=\operatorname{Spec}k\amalg B\operatorname{GL}_{1}\amalg B\operatorname{GL}_{2}\amalg \ldots .\end{eqnarray}$$
Algebroids
There is a canonical sheaf of algebras
![]() $\mathfrak{A}\rightarrow \mathfrak{M}$
over
$\mathfrak{A}\rightarrow \mathfrak{M}$
over
![]() $\mathfrak{M}$
. The set of sections of
$\mathfrak{M}$
. The set of sections of
![]() $\mathfrak{A}$
over the
$\mathfrak{A}$
over the
![]() $S$
-valued point
$S$
-valued point
![]() $x$
of
$x$
of
![]() $\mathfrak{M}$
is the
$\mathfrak{M}$
is the
![]() $\mathscr{O}(S)$
-algebra
$\mathscr{O}(S)$
-algebra
![]() $\mathfrak{A}_{x}=\operatorname{End}(x)$
. For
$\mathfrak{A}_{x}=\operatorname{End}(x)$
. For
![]() $\mathfrak{M}=\mathfrak{Vect}$
, the point
$\mathfrak{M}=\mathfrak{Vect}$
, the point
![]() $x$
is a vector bundle over
$x$
is a vector bundle over
![]() $S$
, and
$S$
, and
![]() $\operatorname{End}(x)$
is the
$\operatorname{End}(x)$
is the
![]() $\mathscr{O}(S)$
-module of endomorphisms of
$\mathscr{O}(S)$
-module of endomorphisms of
![]() $x$
.
$x$
.
There is also a canonical isomorphism of group sheaves
![]() $\mathfrak{A}^{\times }\rightarrow I_{\mathfrak{M}}$
over
$\mathfrak{A}^{\times }\rightarrow I_{\mathfrak{M}}$
over
![]() $\mathfrak{M}$
, where
$\mathfrak{M}$
, where
![]() $I_{\mathfrak{M}}$
is the inertia stack of
$I_{\mathfrak{M}}$
is the inertia stack of
![]() $\mathfrak{M}$
. (Recall that the sections of
$\mathfrak{M}$
. (Recall that the sections of
![]() $I_{\mathfrak{M}}$
over the
$I_{\mathfrak{M}}$
over the
![]() $S$
-valued point
$S$
-valued point
![]() $x$
of
$x$
of
![]() $\mathfrak{M}$
are the automorphisms of
$\mathfrak{M}$
are the automorphisms of
![]() $x$
, in other words, the units in the algebra of endomorphisms.)
$x$
, in other words, the units in the algebra of endomorphisms.)
We call a triple
![]() $(X,A_{X},\unicode[STIX]{x1D704})$
an algebroid (see Definition 1.38 and Remark 1.44) if
$(X,A_{X},\unicode[STIX]{x1D704})$
an algebroid (see Definition 1.38 and Remark 1.44) if
![]() $X$
is an algebraic stack,
$X$
is an algebraic stack,
![]() $A_{X}\rightarrow X$
is a representable sheaf of finite
$A_{X}\rightarrow X$
is a representable sheaf of finite
![]() $\mathscr{O}$
-algebras over
$\mathscr{O}$
-algebras over
![]() $X$
(or finite type algebras, as we call them; see Definition 1.18), and
$X$
(or finite type algebras, as we call them; see Definition 1.18), and
![]() $\unicode[STIX]{x1D704}:A_{X}^{\times }\rightarrow I_{X}$
is an open immersion of relative group schemes over
$\unicode[STIX]{x1D704}:A_{X}^{\times }\rightarrow I_{X}$
is an open immersion of relative group schemes over
![]() $X$
, making the canonical diagram
$X$
, making the canonical diagram

commute.
So,
![]() $\mathfrak{M}$
with its canonical sheaf of algebras
$\mathfrak{M}$
with its canonical sheaf of algebras
![]() $\mathfrak{A}$
is an example of an algebroid. In this case,
$\mathfrak{A}$
is an example of an algebroid. In this case,
![]() $\unicode[STIX]{x1D704}$
is an isomorphism, yielding what we call a strict algebroid.
$\unicode[STIX]{x1D704}$
is an isomorphism, yielding what we call a strict algebroid.
Algebroids are generalizations of linear algebraic stacks (they are linear over their coarse moduli spaces, if they are strict). They are slightly more flexible. For example, schemes can be considered as algebroids in a canonical way. If the algebraic stack
![]() $X$
is the base of an algebroid, then the connected component
$X$
is the base of an algebroid, then the connected component
![]() $I_{X}^{\circ }$
of its inertia stack
$I_{X}^{\circ }$
of its inertia stack
![]() $I_{X}$
is the group of units in an algebra. This is the main significance of algebroids for us.
$I_{X}$
is the group of units in an algebra. This is the main significance of algebroids for us.
Just like algebraic stacks, algebroids form a 2-category, in which 2-fibred products exist. Whenever
![]() $(X,A_{X})$
is an algebroid, and
$(X,A_{X})$
is an algebroid, and
![]() $Y\rightarrow X$
is an inert morphism of algebraic stacks, i.e.,
$Y\rightarrow X$
is an inert morphism of algebraic stacks, i.e.,
![]() $I_{Y}^{\circ }=I_{X}^{\circ }|_{Y}$
(see Definition 1.47), the stack
$I_{Y}^{\circ }=I_{X}^{\circ }|_{Y}$
(see Definition 1.47), the stack
![]() $Y$
is endowed with a natural structure of an algebroid via
$Y$
is endowed with a natural structure of an algebroid via
![]() $A_{X}|_{Y}$
. Examples of inert morphisms include monomorphisms and projections
$A_{X}|_{Y}$
. Examples of inert morphisms include monomorphisms and projections
![]() $Z\times X\rightarrow X$
, for schemes
$Z\times X\rightarrow X$
, for schemes
![]() $Z$
. A locally closed immersion of algebroids
$Z$
. A locally closed immersion of algebroids
![]() $(Y,A_{Y})\rightarrow (X,A_{X})$
is a morphism where
$(Y,A_{Y})\rightarrow (X,A_{X})$
is a morphism where
![]() $Y\rightarrow X$
is a locally closed immersion of algebraic stacks, such that
$Y\rightarrow X$
is a locally closed immersion of algebraic stacks, such that
![]() $A_{Y}=A_{X}|_{Y}$
. Every scheme
$A_{Y}=A_{X}|_{Y}$
. Every scheme
![]() $Z$
is an algebroid via the definition
$Z$
is an algebroid via the definition
![]() $A_{Z}=0_{Z}$
.
$A_{Z}=0_{Z}$
.
A key observation is that if
![]() $(X,A)$
is an algebroid, then
$(X,A)$
is an algebroid, then
![]() $(I_{X},I_{A})$
is another algebroid. In fact,
$(I_{X},I_{A})$
is another algebroid. In fact,
![]() $I_{A}$
, the inertia stack of the stack
$I_{A}$
, the inertia stack of the stack
![]() $A$
(the total ‘space’ of the sheaf of algebras
$A$
(the total ‘space’ of the sheaf of algebras
![]() $A$
), is equal to the subalgebra of
$A$
), is equal to the subalgebra of
![]() $A|_{I_{X}}$
fixed under its tautological automorphism. We call
$A|_{I_{X}}$
fixed under its tautological automorphism. We call
![]() $(I_{X},I_{A})$
the inertia algebroid of
$(I_{X},I_{A})$
the inertia algebroid of
![]() $(X,A)$
. It comes with a canonical morphism to
$(X,A)$
. It comes with a canonical morphism to
![]() $(X,A)$
. There is also a semi-simple connected version of the algebroid inertia, denoted by
$(X,A)$
. There is also a semi-simple connected version of the algebroid inertia, denoted by
![]() $I^{\circ ,\text{ss}}$
.
$I^{\circ ,\text{ss}}$
.
The motivic Hall algebra
We define stack functions to be representable morphisms of algebroids
![]() $(X,A_{X})\rightarrow (\mathfrak{M},\mathfrak{A})$
, where
$(X,A_{X})\rightarrow (\mathfrak{M},\mathfrak{A})$
, where
![]() $X$
is of finite type. The Hall algebra
$X$
is of finite type. The Hall algebra
![]() $K(\mathfrak{M})$
of
$K(\mathfrak{M})$
of
![]() $\mathfrak{M}$
is the
$\mathfrak{M}$
is the
![]() $\mathbb{Q}$
-vector space on the isomorphism classes of stack functions modulo the scissor relations relative
$\mathbb{Q}$
-vector space on the isomorphism classes of stack functions modulo the scissor relations relative
![]() $\mathfrak{M}$
:
$\mathfrak{M}$
:
and the inert bundle relations relative
![]() $\mathfrak{M}$
:
$\mathfrak{M}$
:
Here,
![]() $[X\rightarrow \mathfrak{M}]$
denotes the Hall algebra element defined by a stack function with base
$[X\rightarrow \mathfrak{M}]$
denotes the Hall algebra element defined by a stack function with base
![]() $X$
. Also,
$X$
. Also,
![]() $Z\rightarrow X$
is a closed immersion of algebroids, with open complement
$Z\rightarrow X$
is a closed immersion of algebroids, with open complement
![]() $X\setminus Z$
, and
$X\setminus Z$
, and
![]() $Y\rightarrow X$
is an inert fibre bundle (Definition 1.53) with special structure group and fibre
$Y\rightarrow X$
is an inert fibre bundle (Definition 1.53) with special structure group and fibre
![]() $F$
, all endowed with their canonical algebroid structure. (Examples of inert fibre bundles are étale locally trivial ones.)
$F$
, all endowed with their canonical algebroid structure. (Examples of inert fibre bundles are étale locally trivial ones.)
We have the following structures on the Hall algebra.
(i) Module structure. Let
 $K(\text{Var})$
denote the Grothendieck ring of varieties over
$K(\text{Var})$
denote the Grothendieck ring of varieties over
 $k$
. We denote the motivic weight of the affine line by
$k$
. We denote the motivic weight of the affine line by
 $q=[\mathbb{A}^{1}]\in K(\text{Var})$
. By
$q=[\mathbb{A}^{1}]\in K(\text{Var})$
. By
 $[Z]\cdot [X\rightarrow \mathfrak{M}]=[Z\times X\rightarrow \mathfrak{M}]$
we define a
$[Z]\cdot [X\rightarrow \mathfrak{M}]=[Z\times X\rightarrow \mathfrak{M}]$
we define a
 $K(\text{Var})$
-module structure on
$K(\text{Var})$
-module structure on
 $K(\mathfrak{M})$
.
$K(\mathfrak{M})$
.(ii) Multiplication. By
 $[X\rightarrow \mathfrak{M}]\cdot [Y\rightarrow \mathfrak{M}]=[X\times Y\rightarrow \mathfrak{M}\times \mathfrak{M}\stackrel{\oplus }{\longrightarrow }\mathfrak{M}]$
we define a commutative multiplication on
$[X\rightarrow \mathfrak{M}]\cdot [Y\rightarrow \mathfrak{M}]=[X\times Y\rightarrow \mathfrak{M}\times \mathfrak{M}\stackrel{\oplus }{\longrightarrow }\mathfrak{M}]$
we define a commutative multiplication on
 $K(\mathfrak{M})$
, and
$K(\mathfrak{M})$
, and
 $K(\mathfrak{M})$
is a
$K(\mathfrak{M})$
is a
 $K(\text{Var})$
-algebra with this multiplication.
$K(\text{Var})$
-algebra with this multiplication.(iii) Hall product. Using the stack of short exact sequences in
 $\mathfrak{M}$
, we can define a Hall algebra product
$\mathfrak{M}$
, we can define a Hall algebra product
 $[X\rightarrow \mathfrak{M}]\ast [Y\rightarrow \mathfrak{M}]$
on
$[X\rightarrow \mathfrak{M}]\ast [Y\rightarrow \mathfrak{M}]$
on
 $K(\mathfrak{M})$
. For details, see § 3. The module
$K(\mathfrak{M})$
. For details, see § 3. The module
 $K(\mathfrak{M})$
is a
$K(\mathfrak{M})$
is a
 $K(\text{Var})$
-algebra also with respect to the Hall product.
$K(\text{Var})$
-algebra also with respect to the Hall product.(iv) Unit. The unit with respect to both products is represented by
 $1=[\operatorname{Spec}k\stackrel{0}{\longrightarrow }\mathfrak{M}]$
.
$1=[\operatorname{Spec}k\stackrel{0}{\longrightarrow }\mathfrak{M}]$
.(v) Inertia endomorphism. The algebroid inertia defines an operator
 $I:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
via
$I:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
via
 $I[X\rightarrow \mathfrak{M}]=[I_{X}\rightarrow X\rightarrow \mathfrak{M}]$
. This inertia operator is linear over
$I[X\rightarrow \mathfrak{M}]=[I_{X}\rightarrow X\rightarrow \mathfrak{M}]$
. This inertia operator is linear over
 $K(\text{Var})$
and multiplicative,
$K(\text{Var})$
and multiplicative,
 $I(x\cdot y)=I(x)\cdot I(y)$
, with respect to the commutative multiplication. The same facts hold for the connected semi-simple inertia operator
$I(x\cdot y)=I(x)\cdot I(y)$
, with respect to the commutative multiplication. The same facts hold for the connected semi-simple inertia operator
 $I^{\circ ,\text{ss}}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
.
$I^{\circ ,\text{ss}}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
.
There is also a ‘non-representable’ version of the Hall algebra, where we drop the representability requirement for stack functions and simply define a stack function to be a morphism of algebroids
![]() $X\rightarrow \mathfrak{M}$
, with
$X\rightarrow \mathfrak{M}$
, with
![]() $X$
of finite type. The representable Hall algebra is a subalgebra (with respect to both products) of the non-representable one. Our results on the diagonalizability of the various operators
$X$
of finite type. The representable Hall algebra is a subalgebra (with respect to both products) of the non-representable one. Our results on the diagonalizability of the various operators
![]() $I$
,
$I$
,
![]() $I^{\circ ,\text{ss}}$
,
$I^{\circ ,\text{ss}}$
,
![]() $E_{n}$
hold true also in the non-representable Hall algebra, but the algebraic results on the structure of the Hall algebra need representability. For simplicity, we restrict ourselves therefore to the representable case from the beginning.
$E_{n}$
hold true also in the non-representable Hall algebra, but the algebraic results on the structure of the Hall algebra need representability. For simplicity, we restrict ourselves therefore to the representable case from the beginning.
Usually, when defining the Hall algebra of
![]() $\mathfrak{M}$
, one requires the bundle relations also for non-inert morphisms. The connected inertia operator does not respect such relations, and we therefore do not include them.
$\mathfrak{M}$
, one requires the bundle relations also for non-inert morphisms. The connected inertia operator does not respect such relations, and we therefore do not include them.
Example
A stack function
![]() $X\rightarrow \mathfrak{Vect}$
is the same thing as an algebroid
$X\rightarrow \mathfrak{Vect}$
is the same thing as an algebroid
![]() $(X,A)$
together with a faithful representation, i.e., a vector bundle
$(X,A)$
together with a faithful representation, i.e., a vector bundle
![]() $V$
over
$V$
over
![]() $X$
together with a monomorphism of algebras
$X$
together with a monomorphism of algebras
![]() $A\rightarrow \operatorname{End}(V)$
, making the canonical diagram
$A\rightarrow \operatorname{End}(V)$
, making the canonical diagram
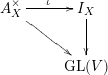
commute.
Examples of stack functions with values in
![]() $\mathfrak{Vect}$
include subalgebras
$\mathfrak{Vect}$
include subalgebras
![]() $A\subset M_{n\times n}$
. (The induced morphism of algebroids is
$A\subset M_{n\times n}$
. (The induced morphism of algebroids is
![]() $(BA^{\times },A^{\times }\backslash A)\rightarrow (B\operatorname{GL}_{n},\operatorname{GL}_{n}\backslash M_{n\times n})$
.) The elements of
$(BA^{\times },A^{\times }\backslash A)\rightarrow (B\operatorname{GL}_{n},\operatorname{GL}_{n}\backslash M_{n\times n})$
.) The elements of
![]() $K(\mathfrak{Vect})$
defined by
$K(\mathfrak{Vect})$
defined by
![]() $A\subset M_{n\times n}$
and
$A\subset M_{n\times n}$
and
![]() $B\subset M_{n\times n}$
are equal if and only if
$B\subset M_{n\times n}$
are equal if and only if
![]() $A$
and
$A$
and
![]() $B$
are conjugate in
$B$
are conjugate in
![]() $M_{n\times n}$
.
$M_{n\times n}$
.
The subalgebra
![]() $U$
of
$U$
of
![]() $K(\mathfrak{Vect})$
with respect to the Hall product, generated by the
$K(\mathfrak{Vect})$
with respect to the Hall product, generated by the
![]() $[n]=[B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]$
, is free on these elements
$[n]=[B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]$
, is free on these elements
![]() $[n]$
, for
$[n]$
, for
![]() $n>0$
, as a unitary
$n>0$
, as a unitary
![]() $\mathbb{Q}$
-algebra. In the literature,
$\mathbb{Q}$
-algebra. In the literature,
![]() $U$
is known as the Hopf algebra of non-commutative symmetric functions; see [Reference CartierCar07, Example 4.1(F)].
$U$
is known as the Hopf algebra of non-commutative symmetric functions; see [Reference CartierCar07, Example 4.1(F)].
(If we add the (non-inert) vector bundle relations relative to
![]() $\mathfrak{Vect}$
, see, e.g., [Reference BridgelandBri12], we get
$\mathfrak{Vect}$
, see, e.g., [Reference BridgelandBri12], we get
Here
![]() $n=\sum \unicode[STIX]{x1D706}_{i}$
, and
$n=\sum \unicode[STIX]{x1D706}_{i}$
, and
![]() $\binom{n}{\unicode[STIX]{x1D706}_{1}\ldots \unicode[STIX]{x1D706}_{n}}_{q}$
denotes the
$\binom{n}{\unicode[STIX]{x1D706}_{1}\ldots \unicode[STIX]{x1D706}_{n}}_{q}$
denotes the
![]() $q$
-deformed multinomial coefficient, which gives the motivic weight of the flag variety of type
$q$
-deformed multinomial coefficient, which gives the motivic weight of the flag variety of type
![]() $\unicode[STIX]{x1D706}$
. We have also denoted the parabolic subgroup of
$\unicode[STIX]{x1D706}$
. We have also denoted the parabolic subgroup of
![]() $\operatorname{GL}_{n}$
of type
$\operatorname{GL}_{n}$
of type
![]() $\unicode[STIX]{x1D706}$
by
$\unicode[STIX]{x1D706}$
by
![]() $P(\unicode[STIX]{x1D706})$
. Hence, the
$P(\unicode[STIX]{x1D706})$
. Hence, the
![]() $\mathbb{Q}$
-algebra obtained by dividing
$\mathbb{Q}$
-algebra obtained by dividing
![]() $U$
by the vector bundle relations is the commutative polynomial algebra over
$U$
by the vector bundle relations is the commutative polynomial algebra over
![]() $\mathbb{Q}$
, on the symbols
$\mathbb{Q}$
, on the symbols
![]() $[1],[2],[3],\ldots$
. This is the Hopf algebra of symmetric functions.)
$[1],[2],[3],\ldots$
. This is the Hopf algebra of symmetric functions.)
The spectrum of semi-simple inertia
The main point of this work is to study the spectral theory of the semi-simple inertia operator
![]() $I^{\circ ,\text{ss}}$
on
$I^{\circ ,\text{ss}}$
on
![]() $K(\mathfrak{M})$
.
$K(\mathfrak{M})$
.
Before announcing our results, let us do a few sample calculations. They contain some of the central ideas of this paper. Only strict algebroids will occur, so we write
![]() $I^{\text{ss}}$
instead of
$I^{\text{ss}}$
instead of
![]() $I^{\circ ,\text{ss}}$
.
$I^{\circ ,\text{ss}}$
.
We consider
![]() $\mathfrak{M}=\mathfrak{Vect}$
. The linear stack of line bundles defines the stack function
$\mathfrak{M}=\mathfrak{Vect}$
. The linear stack of line bundles defines the stack function
![]() $[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
. We have
$[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
. We have
 $$\begin{eqnarray}\displaystyle I^{\text{ss}}[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}] & = & \displaystyle [\operatorname{GL}_{1}^{\text{ss}}\times \,B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\nonumber\\ \displaystyle & = & \displaystyle [\operatorname{GL}_{1}\times \,B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\nonumber\\ \displaystyle & = & \displaystyle (q-1)[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\text{ss}}[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}] & = & \displaystyle [\operatorname{GL}_{1}^{\text{ss}}\times \,B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\nonumber\\ \displaystyle & = & \displaystyle [\operatorname{GL}_{1}\times \,B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]\nonumber\\ \displaystyle & = & \displaystyle (q-1)[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}].\nonumber\end{eqnarray}$$
This proves that
![]() $[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]$
is an eigenvector of
$[B\operatorname{GL}_{1}\rightarrow \mathfrak{Vect}]$
is an eigenvector of
![]() $I^{\text{ss}}$
, with corresponding eigenvalue
$I^{\text{ss}}$
, with corresponding eigenvalue
![]() $(q-1)\in K(\text{Var})$
.
$(q-1)\in K(\text{Var})$
.
Because
![]() $I^{\text{ss}}$
is an algebra morphism with respect to the commutative product, it immediately follows that every
$I^{\text{ss}}$
is an algebra morphism with respect to the commutative product, it immediately follows that every
![]() $(q-1)^{r}$
for
$(q-1)^{r}$
for
![]() $r\geqslant 0$
is an eigenvalue of
$r\geqslant 0$
is an eigenvalue of
![]() $I^{\text{ss}}$
, with corresponding eigenvector
$I^{\text{ss}}$
, with corresponding eigenvector
![]() $[B\operatorname{GL}_{1}^{r}\rightarrow B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
.
$[B\operatorname{GL}_{1}^{r}\rightarrow B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
.
These are not the only eigenvalues of
![]() $I^{\text{ss}}$
. In fact, let us consider the stack function of all rank 2 vector bundles
$I^{\text{ss}}$
. In fact, let us consider the stack function of all rank 2 vector bundles
![]() $[B\operatorname{GL}_{2}\rightarrow \mathfrak{Vect}]$
. Recall that the inertia stack of
$[B\operatorname{GL}_{2}\rightarrow \mathfrak{Vect}]$
. Recall that the inertia stack of
![]() $B\operatorname{GL}_{2}$
is the quotient stack
$B\operatorname{GL}_{2}$
is the quotient stack
![]() $\operatorname{GL}_{2}/_{\text{ad}}\operatorname{GL}_{2}$
, where
$\operatorname{GL}_{2}/_{\text{ad}}\operatorname{GL}_{2}$
, where
![]() $\operatorname{GL}_{2}$
acts on itself by the adjoint action. The semi-simple part of
$\operatorname{GL}_{2}$
acts on itself by the adjoint action. The semi-simple part of
![]() $\operatorname{GL}_{2}$
decomposes as
$\operatorname{GL}_{2}$
decomposes as
![]() $\operatorname{GL}_{2}^{\text{eq}}\sqcup \operatorname{GL}_{2}^{\text{neq}}$
, according to whether the two eigenvalues of an element of
$\operatorname{GL}_{2}^{\text{eq}}\sqcup \operatorname{GL}_{2}^{\text{neq}}$
, according to whether the two eigenvalues of an element of
![]() $\operatorname{GL}_{2}$
are equal or not equal. By the scissor relations, we have
$\operatorname{GL}_{2}$
are equal or not equal. By the scissor relations, we have
 $$\begin{eqnarray}\displaystyle I^{\text{ss}}[B\operatorname{GL}_{2}] & = & \displaystyle [\operatorname{GL}_{2}^{\text{eq}}/_{\text{ad}}\operatorname{GL}_{2}]+[\operatorname{GL}_{2}^{\text{neq}}/_{\text{ad}}\operatorname{GL}_{2}]\nonumber\\ \displaystyle & = & \displaystyle [\unicode[STIX]{x1D6E5}\times B\operatorname{GL}_{2}]+[T^{\ast }/_{\text{ad}}N]\nonumber\\ \displaystyle & = & \displaystyle (q-1)[B\operatorname{GL}_{2}]+x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\text{ss}}[B\operatorname{GL}_{2}] & = & \displaystyle [\operatorname{GL}_{2}^{\text{eq}}/_{\text{ad}}\operatorname{GL}_{2}]+[\operatorname{GL}_{2}^{\text{neq}}/_{\text{ad}}\operatorname{GL}_{2}]\nonumber\\ \displaystyle & = & \displaystyle [\unicode[STIX]{x1D6E5}\times B\operatorname{GL}_{2}]+[T^{\ast }/_{\text{ad}}N]\nonumber\\ \displaystyle & = & \displaystyle (q-1)[B\operatorname{GL}_{2}]+x.\nonumber\end{eqnarray}$$
Here,
![]() $\unicode[STIX]{x1D6E5}$
is the one-parameter subgroup of scalar matrices, and
$\unicode[STIX]{x1D6E5}$
is the one-parameter subgroup of scalar matrices, and
![]() $T$
is the maximal torus of diagonal matrices in
$T$
is the maximal torus of diagonal matrices in
![]() $\operatorname{GL}_{2}$
. Further notation:
$\operatorname{GL}_{2}$
. Further notation:
![]() $T^{\ast }=T\setminus \unicode[STIX]{x1D6E5}$
,
$T^{\ast }=T\setminus \unicode[STIX]{x1D6E5}$
,
![]() $N$
is the normalizer of
$N$
is the normalizer of
![]() $T$
in
$T$
in
![]() $\operatorname{GL}_{2}$
, and
$\operatorname{GL}_{2}$
, and
![]() $x=[T^{\ast }/_{\text{ad}}N]$
.
$x=[T^{\ast }/_{\text{ad}}N]$
.
Next, we calculate
![]() $I^{\text{ss}}x$
. In fact, we have
$I^{\text{ss}}x$
. In fact, we have
![]() $I_{T^{\ast }/N}^{\text{ss}}=I_{T^{\ast }/N}=(T^{\ast }\times T)/N$
, by the ‘stabilizer formula’ for the inertia stack of a quotient stack
$I_{T^{\ast }/N}^{\text{ss}}=I_{T^{\ast }/N}=(T^{\ast }\times T)/N$
, by the ‘stabilizer formula’ for the inertia stack of a quotient stack
We note that
![]() $N=T\rtimes \mathbb{Z}_{2}$
acts on
$N=T\rtimes \mathbb{Z}_{2}$
acts on
![]() $T^{\ast }\times T$
diagonally, via its quotient
$T^{\ast }\times T$
diagonally, via its quotient
![]() $\mathbb{Z}_{2}$
, by swapping the entries of
$\mathbb{Z}_{2}$
, by swapping the entries of
![]() $T$
. We embed
$T$
. We embed
![]() $T$
into
$T$
into
![]() $\mathbb{A}^{2}$
equivariantly with respect to
$\mathbb{A}^{2}$
equivariantly with respect to
![]() $\mathbb{Z}_{2}$
and then decompose
$\mathbb{Z}_{2}$
and then decompose
![]() $\mathbb{A}^{2}$
as
$\mathbb{A}^{2}$
as
![]() $T\sqcup (\operatorname{GL}_{1}\times 0)\sqcup (0\times \operatorname{GL}_{1})\sqcup (0,0)$
. This gives
$T\sqcup (\operatorname{GL}_{1}\times 0)\sqcup (0\times \operatorname{GL}_{1})\sqcup (0,0)$
. This gives
We have a pullback diagram of algebroids.

It shows that the vector bundle
![]() $(T^{\ast }\times \mathbb{A}^{2})/N\rightarrow T^{\ast }/N$
is a pullback of the vector bundle
$(T^{\ast }\times \mathbb{A}^{2})/N\rightarrow T^{\ast }/N$
is a pullback of the vector bundle
![]() $(T^{\ast }\times \mathbb{A}^{2})/\mathbb{Z}_{2}\rightarrow T^{\ast }/\mathbb{Z}_{2}$
. The latter is a vector bundle over a scheme, and is therefore Zariski-locally trivial by Hilbert’s Theorem 90. The same is then true for any pullback bundle. Hence, we conclude that
$(T^{\ast }\times \mathbb{A}^{2})/\mathbb{Z}_{2}\rightarrow T^{\ast }/\mathbb{Z}_{2}$
. The latter is a vector bundle over a scheme, and is therefore Zariski-locally trivial by Hilbert’s Theorem 90. The same is then true for any pullback bundle. Hence, we conclude that
using the scissor relations, or the inert bundle relations. So, from (1), we conclude that
which we solve for
![]() $I^{\text{ss}}x$
to get
$I^{\text{ss}}x$
to get
We already know that
![]() $I^{\text{ss}}[BT]=(q-1)^{2}[BT]$
, and so we conclude that
$I^{\text{ss}}[BT]=(q-1)^{2}[BT]$
, and so we conclude that
![]() $[B\operatorname{GL}_{2}]$
,
$[B\operatorname{GL}_{2}]$
,
![]() $x$
, and
$x$
, and
![]() $[BT]$
generate an
$[BT]$
generate an
![]() $I^{\text{ss}}$
-invariant subspace of
$I^{\text{ss}}$
-invariant subspace of
![]() $K(\mathfrak{Vect})$
, and the matrix of
$K(\mathfrak{Vect})$
, and the matrix of
![]() $I^{\text{ss}}$
on this subspace is
$I^{\text{ss}}$
on this subspace is
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}q-1 & 0 & 0\\ 1 & q^{2}-1 & 0\\ 0 & -(q-1)^{2}(q-2) & (q-1)^{2}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}q-1 & 0 & 0\\ 1 & q^{2}-1 & 0\\ 0 & -(q-1)^{2}(q-2) & (q-1)^{2}\end{array}\right).\end{eqnarray}$$
This matrix is lower triangular, with distinct scalars on the diagonal, and is therefore diagonalizable over the field
![]() $\mathbb{Q}(q)$
. So, on this subspace,
$\mathbb{Q}(q)$
. So, on this subspace,
![]() $I^{\text{ss}}$
is diagonalizable, with eigenvalues
$I^{\text{ss}}$
is diagonalizable, with eigenvalues
![]() $(q-1)$
,
$(q-1)$
,
![]() $(q^{2}-1)$
, and
$(q^{2}-1)$
, and
![]() $(q-1)^{2}$
. If we decompose
$(q-1)^{2}$
. If we decompose
![]() $[B\operatorname{GL}_{2}]$
as a sum of eigenvectors, we get the eigenvectors
$[B\operatorname{GL}_{2}]$
as a sum of eigenvectors, we get the eigenvectors
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}lcl@{}}[B\operatorname{GL}_{2}]-{\displaystyle \frac{1}{q(q-1)}}x-{\displaystyle \frac{1}{q}}[BT]\quad & \text{with eigenvalue}\ & (q-1),\\ {\displaystyle \frac{1}{q(q-1)}}x-{\displaystyle \frac{q-2}{2q}}[BT]\quad & \text{with eigenvalue}\ & (q^{2}-1),\\ {\textstyle \frac{1}{2}}[BT]\quad & \text{with eigenvalue}\ & (q-1)^{2}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}lcl@{}}[B\operatorname{GL}_{2}]-{\displaystyle \frac{1}{q(q-1)}}x-{\displaystyle \frac{1}{q}}[BT]\quad & \text{with eigenvalue}\ & (q-1),\\ {\displaystyle \frac{1}{q(q-1)}}x-{\displaystyle \frac{q-2}{2q}}[BT]\quad & \text{with eigenvalue}\ & (q^{2}-1),\\ {\textstyle \frac{1}{2}}[BT]\quad & \text{with eigenvalue}\ & (q-1)^{2}.\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
A very important observation is that when we add together the eigencomponents whose eigenvalues have the same order of vanishing at
![]() $q=1$
, we get coefficients in
$q=1$
, we get coefficients in
![]() $\mathbb{Q}$
, instead of
$\mathbb{Q}$
, instead of
![]() $\mathbb{Q}(q)$
. In the above example, we add together the components of
$\mathbb{Q}(q)$
. In the above example, we add together the components of
![]() $[B\operatorname{GL}_{2}]$
with eigenvalues
$[B\operatorname{GL}_{2}]$
with eigenvalues
![]() $(q-1)$
and
$(q-1)$
and
![]() $(q^{2}-1)$
to obtain
$(q^{2}-1)$
to obtain
![]() $[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
.
$[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
.
Another important observation is that diagonalizing
![]() $I^{\text{ss}}$
does not, despite appearances, require us to invert
$I^{\text{ss}}$
does not, despite appearances, require us to invert
![]() $(q-1)$
. In fact, the algebroid
$(q-1)$
. In fact, the algebroid
![]() $x$
appearing in the above argument is divisible by
$x$
appearing in the above argument is divisible by
![]() $(q-1)$
, although the quotient is not a strict algebroid any longer. To see this, consider the action of
$(q-1)$
, although the quotient is not a strict algebroid any longer. To see this, consider the action of
![]() $\mathbb{G}_{m}$
on
$\mathbb{G}_{m}$
on
![]() $T^{\ast }$
by left multiplication. It commutes with the adjoint action by
$T^{\ast }$
by left multiplication. It commutes with the adjoint action by
![]() $N$
. Let us denote the quotient
$N$
. Let us denote the quotient
![]() $\mathbb{G}_{m}\backslash T^{\ast }$
by
$\mathbb{G}_{m}\backslash T^{\ast }$
by
![]() $\widetilde{T}^{\ast }$
. We can endow the stack
$\widetilde{T}^{\ast }$
. We can endow the stack
![]() $\widetilde{T}^{\ast }/N$
with the structure of an algebroid, making the quotient map
$\widetilde{T}^{\ast }/N$
with the structure of an algebroid, making the quotient map
![]() $T^{\ast }/N\rightarrow \widetilde{T}^{\ast }/N$
into an inert morphism of algebroids with fibre
$T^{\ast }/N\rightarrow \widetilde{T}^{\ast }/N$
into an inert morphism of algebroids with fibre
![]() $\mathbb{G}_{m}$
. (For the details, see Proposition 1.61.) The inert bundle relations then imply that
$\mathbb{G}_{m}$
. (For the details, see Proposition 1.61.) The inert bundle relations then imply that
![]() $x=[T^{\ast }/N]$
is indeed divisible by
$x=[T^{\ast }/N]$
is indeed divisible by
![]() $(q-1)$
.
$(q-1)$
.
The matrices in
![]() $\widetilde{T}^{\ast }$
of trace zero have the full group
$\widetilde{T}^{\ast }$
of trace zero have the full group
![]() $N$
as stabilizer. Decomposing
$N$
as stabilizer. Decomposing
![]() $\widetilde{T}^{\ast }$
into matrices of trace zero, and matrices of non-zero trace, we see that
$\widetilde{T}^{\ast }$
into matrices of trace zero, and matrices of non-zero trace, we see that
Hence,
![]() $\widetilde{T}^{\ast }/N$
is not a strict algebroid, as
$\widetilde{T}^{\ast }/N$
is not a strict algebroid, as
![]() $N$
is not connected, and is not the group of units in any algebra. This is, in fact, the reason for considering non-strict algebroids at all. (For more on this, see Example 2.18.)
$N$
is not connected, and is not the group of units in any algebra. This is, in fact, the reason for considering non-strict algebroids at all. (For more on this, see Example 2.18.)
(In the above calculations, we have suppressed the algebra part
![]() $A$
of the various algebroids
$A$
of the various algebroids
![]() $(X,A)$
. We leave it to the reader to supply the natural algebra for each algebroid mentioned.)
$(X,A)$
. We leave it to the reader to supply the natural algebra for each algebroid mentioned.)
Results
We now summarize the main results of this paper.
Theorem 1 (Diagonalizability of
 $I^{\circ ,\text{ss}}$
).
$I^{\circ ,\text{ss}}$
).
The operator
![]() $I^{\circ ,\text{ss}}$
on
$I^{\circ ,\text{ss}}$
on
is diagonalizable, the eigenvalues are indexed by partitions
![]() $\unicode[STIX]{x1D706}$
, and the eigenvalue corresponding to the partition
$\unicode[STIX]{x1D706}$
, and the eigenvalue corresponding to the partition
![]() $\unicode[STIX]{x1D706}$
is the cyclotomic polynomial
$\unicode[STIX]{x1D706}$
is the cyclotomic polynomial
In other words, we have a direct sum decomposition
into subspaces invariant under
![]() $I^{\circ ,\text{ss}}$
, and
$I^{\circ ,\text{ss}}$
, and
![]() $I^{\circ ,\text{ss}}|_{K^{\unicode[STIX]{x1D706}}(\mathfrak{M})}$
is multiplication by
$I^{\circ ,\text{ss}}|_{K^{\unicode[STIX]{x1D706}}(\mathfrak{M})}$
is multiplication by
![]() $\mathscr{Q}(\unicode[STIX]{x1D706})$
.
$\mathscr{Q}(\unicode[STIX]{x1D706})$
.
The same theorem holds for the operator
![]() $I^{\text{ss}}$
in the context of strict algebroids. We also prove a stronger version avoiding denominators divisible by
$I^{\text{ss}}$
in the context of strict algebroids. We also prove a stronger version avoiding denominators divisible by
![]() $(q-1)$
, but this version only works for algebroids.
$(q-1)$
, but this version only works for algebroids.
The proof of this theorem is a generalization of the above sample calculation for the stack of rank 2 vector bundles. One goal of § 1 is to set up the necessary notation.
Theorem 2 (Graded structure of
 $K(\mathfrak{M})$
).
$K(\mathfrak{M})$
).
There is a direct sum decomposition
such that
Moreover, the commutative product is graded with respect to (2).
Again, the same theorem holds in the context of strict algebroids.
The fact about the gradedness of the commutative product is expected from the fact that the semi-simple inertia respects the commutative product (it follows from this fact over
![]() $\mathbb{Q}(q)$
, but is true over
$\mathbb{Q}(q)$
, but is true over
![]() $\mathbb{Q}$
).
$\mathbb{Q}$
).
Geometrically, the descending filtration
![]() $K^{{\geqslant}r}(\mathfrak{M})$
induced by the grading (2) can be described as follows:
$K^{{\geqslant}r}(\mathfrak{M})$
induced by the grading (2) can be described as follows:
![]() $K^{{\geqslant}r}(\mathfrak{M})$
is the
$K^{{\geqslant}r}(\mathfrak{M})$
is the
![]() $\mathbb{Q}$
-span of all stack functions
$\mathbb{Q}$
-span of all stack functions
![]() $[X\rightarrow \mathfrak{M}]$
, for which the algebra of global sections
$[X\rightarrow \mathfrak{M}]$
, for which the algebra of global sections
![]() $\unicode[STIX]{x1D6E4}(X,A_{X})$
admits at least
$\unicode[STIX]{x1D6E4}(X,A_{X})$
admits at least
![]() $r$
orthogonal non-zero central idempotents, where
$r$
orthogonal non-zero central idempotents, where
![]() $A_{X}$
is the algebra of the algebroid
$A_{X}$
is the algebra of the algebroid
![]() $(X,A_{X})$
.
$(X,A_{X})$
.
The direct summands
![]() $K^{r}(\mathfrak{M})$
are the common eigenspaces of the family of commuting operators
$K^{r}(\mathfrak{M})$
are the common eigenspaces of the family of commuting operators
![]() $(E_{n})_{n\geqslant 0}$
, where
$(E_{n})_{n\geqslant 0}$
, where
![]() $E_{n}(X)$
is the stack of decompositions of
$E_{n}(X)$
is the stack of decompositions of
![]() $1\in A_{X}$
into a sum of
$1\in A_{X}$
into a sum of
![]() $n$
orthogonal labelled idempotents. The eigenvalues of the operators
$n$
orthogonal labelled idempotents. The eigenvalues of the operators
![]() $E_{n}$
are integers, and the whole family of operators
$E_{n}$
are integers, and the whole family of operators
![]() $(E_{n})$
is diagonalizable over
$(E_{n})$
is diagonalizable over
![]() $\mathbb{Q}$
. The proof of this fact proceeds by proving that the
$\mathbb{Q}$
. The proof of this fact proceeds by proving that the
![]() $(E_{n})$
preserve the descending filtration described geometrically above and have distinct integer diagonal entries.
$(E_{n})$
preserve the descending filtration described geometrically above and have distinct integer diagonal entries.
It turns out that the ascending filtration
![]() $K^{{\leqslant}n}(\mathfrak{M})$
associated with the grading in the above theorem can be described as
$K^{{\leqslant}n}(\mathfrak{M})$
associated with the grading in the above theorem can be described as
Let us also point out that
where
![]() $K(\text{DM})$
is the Grothendieck
$K(\text{DM})$
is the Grothendieck
![]() $\mathbb{Q}$
-algebra of Deligne–Mumford stacks (see § 2). For this reason,
$\mathbb{Q}$
-algebra of Deligne–Mumford stacks (see § 2). For this reason,
![]() $K(\text{DM})$
is a more natural ring of scalars than
$K(\text{DM})$
is a more natural ring of scalars than
![]() $K(\text{Var})$
, and we will use
$K(\text{Var})$
, and we will use
![]() $K(\text{DM})$
throughout. (On the other hand, in the context of strict algebroids, we have
$K(\text{DM})$
throughout. (On the other hand, in the context of strict algebroids, we have
![]() $K^{0}(\mathfrak{M})=K(\text{Var})$
.)
$K^{0}(\mathfrak{M})=K(\text{Var})$
.)
If we denote by
![]() $\unicode[STIX]{x1D70B}_{r}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
the projection operator onto the summand
$\unicode[STIX]{x1D70B}_{r}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
the projection operator onto the summand
![]() $K^{r}(\mathfrak{M})$
and form the generating series
$K^{r}(\mathfrak{M})$
and form the generating series
![]() $\unicode[STIX]{x1D70B}_{t}=\sum _{r\geqslant 0}\unicode[STIX]{x1D70B}_{r}t^{r}$
, then we have
$\unicode[STIX]{x1D70B}_{t}=\sum _{r\geqslant 0}\unicode[STIX]{x1D70B}_{r}t^{r}$
, then we have
All the above results could be proved for pairs
![]() $(X,A)$
of algebraic stacks
$(X,A)$
of algebraic stacks
![]() $X$
endowed with finite type algebras
$X$
endowed with finite type algebras
![]() $A$
, instead of algebroids or strict algebroids. One simply replaces
$A$
, instead of algebroids or strict algebroids. One simply replaces
![]() $I^{\circ ,\text{ss}}$
by
$I^{\circ ,\text{ss}}$
by
![]() $A^{\times ,\text{ss}}$
.
$A^{\times ,\text{ss}}$
.
Theorem 3 (Filtered nature of the Hall algebra).
The Hall product is filtered with respect to the filtration
![]() $K^{{\leqslant}r}(\mathfrak{M})$
induced by the grading (2). Moreover, for the associated graded algebra, we have
$K^{{\leqslant}r}(\mathfrak{M})$
induced by the grading (2). Moreover, for the associated graded algebra, we have
In other words, if
![]() $x\in K^{{\leqslant}r}(\mathfrak{M})$
and
$x\in K^{{\leqslant}r}(\mathfrak{M})$
and
![]() $y\in K^{{\leqslant}s}(\mathfrak{M})$
, then
$y\in K^{{\leqslant}s}(\mathfrak{M})$
, then
![]() $x\ast y\in K^{{\leqslant}r+s}(\mathfrak{M})$
, and
$x\ast y\in K^{{\leqslant}r+s}(\mathfrak{M})$
, and
The proof of this theorem uses not much more than some simple combinatorics involving relabelling of direct sum decompositions, and compatibilities between direct sum decompositions of short exact sequences and splittings of short exact sequences.
The theorem implies that the one parameter family of algebras
![]() $(\mathscr{K}(\mathfrak{M}),\ast )$
given by the Rees construction
$(\mathscr{K}(\mathfrak{M}),\ast )$
given by the Rees construction
is a deformation quantization of (i.e., a one-parameter flat family of algebras with special fibre) the commutative algebra
![]() $(K(\mathfrak{M}),\cdot )$
. Hence, the graded algebra
$(K(\mathfrak{M}),\cdot )$
. Hence, the graded algebra
![]() $(K(\mathfrak{M}),\cdot )$
inherits a Poisson bracket
$(K(\mathfrak{M}),\cdot )$
inherits a Poisson bracket
![]() $\{,\}$
of degree
$\{,\}$
of degree
![]() $-1$
. In particular,
$-1$
. In particular,
![]() $K^{1}(\mathfrak{M})$
is a Lie algebra, and it turns out that the Lie bracket on
$K^{1}(\mathfrak{M})$
is a Lie algebra, and it turns out that the Lie bracket on
![]() $K^{1}(\mathfrak{M})$
is equal to the commutator bracket associated to
$K^{1}(\mathfrak{M})$
is equal to the commutator bracket associated to
![]() $\ast$
.
$\ast$
.
The filtered algebra
![]() $(K(\mathfrak{M}),\ast )$
is a filtered quantization of the Poisson algebra
$(K(\mathfrak{M}),\ast )$
is a filtered quantization of the Poisson algebra
![]() $(K(\mathfrak{M}),\cdot ,\{,\})$
, as defined in [Reference SchedlerSch16]. Of course, we have more structure here, as our filtration comes from a natural grading, but it is not clear to us what this additional structure on our filtered quantization is useful for.
$(K(\mathfrak{M}),\cdot ,\{,\})$
, as defined in [Reference SchedlerSch16]. Of course, we have more structure here, as our filtration comes from a natural grading, but it is not clear to us what this additional structure on our filtered quantization is useful for.
Following Joyce [Reference JoyceJoy07a], we call
![]() $K^{1}(\mathfrak{M})$
the Lie algebra of virtually indecomposable elements of
$K^{1}(\mathfrak{M})$
the Lie algebra of virtually indecomposable elements of
![]() $K(\mathfrak{M})$
, with the notation
$K(\mathfrak{M})$
, with the notation
![]() $K^{\text{vir}}(\mathfrak{M})=K^{1}(\mathfrak{M})$
.
$K^{\text{vir}}(\mathfrak{M})=K^{1}(\mathfrak{M})$
.
We denote the projection onto
![]() $K^{\text{vir}}(\mathfrak{M})$
by
$K^{\text{vir}}(\mathfrak{M})$
by
![]() $\unicode[STIX]{x1D70B}^{\text{vir}}$
. With this notation, we have, as a special case of (3),
$\unicode[STIX]{x1D70B}^{\text{vir}}$
. With this notation, we have, as a special case of (3),
In terms of eigenspaces of semi-simple inertia, we have
Theorem 4 (Hall algebra logarithms).
Let
![]() $\mathfrak{N}\subset \mathfrak{M}$
be a ‘small enough’ substack, closed under extensions and direct summands, and not intersecting
$\mathfrak{N}\subset \mathfrak{M}$
be a ‘small enough’ substack, closed under extensions and direct summands, and not intersecting
![]() $\operatorname{Spec}k\stackrel{0}{\longrightarrow }\mathfrak{M}$
. Then
$\operatorname{Spec}k\stackrel{0}{\longrightarrow }\mathfrak{M}$
. Then
In particular, the
![]() $\ast$
-logarithm
$\ast$
-logarithm
is virtually indecomposable.
For the precise definition of ‘small enough’, see § 3.3. For example, if
![]() $\mathfrak{M}=\mathfrak{Coh}_{Y}$
for a curve
$\mathfrak{M}=\mathfrak{Coh}_{Y}$
for a curve
![]() $Y$
, we could take
$Y$
, we could take
![]() $\mathfrak{N}$
to consist of all non-zero semi-stable vector bundles of a fixed slope. Since
$\mathfrak{N}$
to consist of all non-zero semi-stable vector bundles of a fixed slope. Since
![]() $\mathfrak{N}$
is typically not of finite type, to make sense of
$\mathfrak{N}$
is typically not of finite type, to make sense of
![]() $[\mathfrak{N}]$
we have to pass to a certain completion
$[\mathfrak{N}]$
we have to pass to a certain completion
![]() $\hat{K}(\mathfrak{M})_{+}$
of
$\hat{K}(\mathfrak{M})_{+}$
of
![]() $K(\mathfrak{M})$
. See § 3.3 for details.
$K(\mathfrak{M})$
. See § 3.3 for details.
Theorem 5 (No poles).
Let
![]() $K(\text{St})$
be the Grothendieck
$K(\text{St})$
be the Grothendieck
![]() $\mathbb{Q}$
-algebra of algebraic stacks, modulo all bundle relations with special structure group (inert or not). Consider the map
$\mathbb{Q}$
-algebra of algebraic stacks, modulo all bundle relations with special structure group (inert or not). Consider the map
 $$\begin{eqnarray}\displaystyle \int :K(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})\nonumber\\ \displaystyle \hspace{0.0pt}[(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})] & \longmapsto & \displaystyle [X],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int :K(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})\nonumber\\ \displaystyle \hspace{0.0pt}[(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})] & \longmapsto & \displaystyle [X],\nonumber\end{eqnarray}$$
which forgets the structure map to
![]() $(\mathfrak{M},\mathfrak{A})$
, and the algebroid structure over the stack
$(\mathfrak{M},\mathfrak{A})$
, and the algebroid structure over the stack
![]() $X$
. If
$X$
. If
![]() $x\in K^{{\leqslant}r}(\mathfrak{M})$
, then
$x\in K^{{\leqslant}r}(\mathfrak{M})$
, then
![]() $(q-1)^{r}\int x$
is a regular element of
$(q-1)^{r}\int x$
is a regular element of
![]() $K(\text{St})$
; i.e., under the identification
$K(\text{St})$
; i.e., under the identification
it can be written with a denominator that does not vanish at
![]() $q=1$
.
$q=1$
.
Moreover, suppose we have a grading monoid
![]() $\unicode[STIX]{x1D6E4}$
for
$\unicode[STIX]{x1D6E4}$
for
![]() $\mathfrak{M}$
:
$\mathfrak{M}$
:
We say that
![]() $x$
has ‘degree’
$x$
has ‘degree’
![]() $\unicode[STIX]{x1D6FE}$
if
$\unicode[STIX]{x1D6FE}$
if
![]() $x\in \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
. We need
$x\in \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
. We need
![]() $\unicode[STIX]{x1D6E4}$
to be endowed with a
$\unicode[STIX]{x1D6E4}$
to be endowed with a
![]() $\mathbb{Z}$
-valued bilinear form
$\mathbb{Z}$
-valued bilinear form
![]() $\unicode[STIX]{x1D712}$
such that for every object
$\unicode[STIX]{x1D712}$
such that for every object
![]() $x$
in
$x$
in
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
$\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
![]() $y$
in
$y$
in
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
:
$\mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
:
(i) every extension of
 $y$
by
$y$
by
 $x$
is in
$x$
is in
 $\mathfrak{M}_{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}$
;
$\mathfrak{M}_{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}$
;(ii) the stack of extensions of
 $y$
by
$y$
by
 $x$
is the quotient of a vector space
$x$
is the quotient of a vector space
 $E_{1}$
by another vector space
$E_{1}$
by another vector space
 $E_{0}$
, acting trivially, such that
$E_{0}$
, acting trivially, such that
 $\dim E_{0}-\dim E_{1}=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
.
$\dim E_{0}-\dim E_{1}=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
.
For the precise assumptions, see § 4.2. They are satisfied if
![]() $\mathfrak{M}=\mathfrak{Rep}_{Q}$
, or if
$\mathfrak{M}=\mathfrak{Rep}_{Q}$
, or if
![]() $\mathfrak{M}=\mathfrak{Coh}_{Y}$
and
$\mathfrak{M}=\mathfrak{Coh}_{Y}$
and
![]() $Y$
is a smooth curve, or, more generally, if
$Y$
is a smooth curve, or, more generally, if
![]() $\mathfrak{M}$
is hereditary.
$\mathfrak{M}$
is hereditary.
Then we have a commutative diagram as follows.

Here we use the
![]() $\unicode[STIX]{x1D6E4}$
-graded integral, which is essentially a generating function, indexed by
$\unicode[STIX]{x1D6E4}$
-graded integral, which is essentially a generating function, indexed by
![]() $\unicode[STIX]{x1D6E4}$
, of the integrals of the components of degree
$\unicode[STIX]{x1D6E4}$
, of the integrals of the components of degree
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
of a given stack function.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
of a given stack function.
The upper horizontal arrow in this diagram is the specialization map, which exists because of Theorem 3. The left vertical arrow exists by the ‘no poles’ theorem (Theorem 5). It is a standard fact that this map is an algebra morphism, i.e., it respects the
![]() $\ast$
-product, if the target
$\ast$
-product, if the target
![]() $K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
is endowed with its
$K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
is endowed with its
![]() $q$
-deformed product twisted by
$q$
-deformed product twisted by
![]() $\unicode[STIX]{x1D712}$
. It is a formal consequence of the commutativity of this diagram that the right vertical map is a morphism of Poisson algebras if the target
$\unicode[STIX]{x1D712}$
. It is a formal consequence of the commutativity of this diagram that the right vertical map is a morphism of Poisson algebras if the target
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
is endowed with its bracket induced by
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
is endowed with its bracket induced by
![]() $\unicode[STIX]{x1D712}$
. We call the right vertical map the semi-classical motivic integral.
$\unicode[STIX]{x1D712}$
. We call the right vertical map the semi-classical motivic integral.
In particular, we deduce that
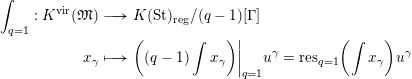 $$\begin{eqnarray}\displaystyle \int _{q=1}:K^{\text{vir}}(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]\nonumber\\ \displaystyle x_{\unicode[STIX]{x1D6FE}} & \longmapsto & \displaystyle \biggl((q-1)\int x_{\unicode[STIX]{x1D6FE}}\biggr)\biggr|_{q=1}u^{\unicode[STIX]{x1D6FE}}=\operatorname{res}_{q=1}\biggl(\int x_{\unicode[STIX]{x1D6FE}}\biggr)u^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{q=1}:K^{\text{vir}}(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]\nonumber\\ \displaystyle x_{\unicode[STIX]{x1D6FE}} & \longmapsto & \displaystyle \biggl((q-1)\int x_{\unicode[STIX]{x1D6FE}}\biggr)\biggr|_{q=1}u^{\unicode[STIX]{x1D6FE}}=\operatorname{res}_{q=1}\biggl(\int x_{\unicode[STIX]{x1D6FE}}\biggr)u^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is a morphism of Lie algebras. The target
![]() $K(\text{St})_{\text{reg}}/(q-1)$
of the semi-classical motivic integral is equal to
$K(\text{St})_{\text{reg}}/(q-1)$
of the semi-classical motivic integral is equal to
![]() $K(\text{Var})/((q-1)+\operatorname{Ann}(q-1))$
.
$K(\text{Var})/((q-1)+\operatorname{Ann}(q-1))$
.
The proof of the no poles theorem combines the above results about the diagonalizability of
![]() $I^{\circ ,\text{ss}}$
, especially in its form avoiding denominators divisible by
$I^{\circ ,\text{ss}}$
, especially in its form avoiding denominators divisible by
![]() $(q-1)$
, with the result that for an algebroid
$(q-1)$
, with the result that for an algebroid
![]() $(X,A)$
, the stack
$(X,A)$
, the stack
![]() $I_{X}^{\circ ,\text{ss}}$
has regular motivic weight, i.e.,
$I_{X}^{\circ ,\text{ss}}$
has regular motivic weight, i.e.,
We think of this as a motivic version of Burnside’s lemma. The more natural-looking conjecture that for an algebraic stack
![]() $X$
, the motivic weight of
$X$
, the motivic weight of
![]() $I_{X}$
is contained in
$I_{X}$
is contained in
![]() $K(\text{Var})\subset K(\text{St})$
is most likely false.
$K(\text{Var})\subset K(\text{St})$
is most likely false.
Discussion
To produce counting invariants for
![]() $\mathfrak{M}$
, we need to look for subcategories
$\mathfrak{M}$
, we need to look for subcategories
![]() $\mathfrak{N}\subset \mathfrak{M}$
, to which we can apply Theorem 4, giving us virtually indecomposable elements
$\mathfrak{N}\subset \mathfrak{M}$
, to which we can apply Theorem 4, giving us virtually indecomposable elements
![]() $\unicode[STIX]{x1D700}[\mathfrak{N}]$
, to which we can apply the integral (4), yielding generating functions with coefficients in
$\unicode[STIX]{x1D700}[\mathfrak{N}]$
, to which we can apply the integral (4), yielding generating functions with coefficients in
![]() $K(\text{St})_{\text{reg}}/(q-1)$
. (See Remark 4.12 for details.) We can apply the Euler characteristic to these elements of
$K(\text{St})_{\text{reg}}/(q-1)$
. (See Remark 4.12 for details.) We can apply the Euler characteristic to these elements of
![]() $K(\text{St})_{\text{reg}}/(q-1)$
to obtain rational numbers. In the hereditary case, the fact that (4) is a morphism of Lie algebras gives the relations among generating functions one is interested in. This leads to wall-crossing formulas, and other results. For details we refer to the works of Joyce, Joyce–Song, and many others.
$K(\text{St})_{\text{reg}}/(q-1)$
to obtain rational numbers. In the hereditary case, the fact that (4) is a morphism of Lie algebras gives the relations among generating functions one is interested in. This leads to wall-crossing formulas, and other results. For details we refer to the works of Joyce, Joyce–Song, and many others.
To deal with the Calabi–Yau 3 case, one needs to insert the correct motivic vanishing cycle weights, to define the integral. This is done by Joyce and Song in [Reference Joyce and SongJS12]. We leave it to future work to supply the details in our context.
The work of Joyce on configurations in abelian categories contains results which correspond to ours, but his definitions are more ad hoc. In fact, one reason for writing the present article was to give a more conceptual treatment of Joyce’s results. We do not prove that our notion of ‘virtual indecomposable object’ coincides with Joyce’s (except for in the case of
![]() $\mathfrak{M}=\mathfrak{Vect}$
, see the appendix), but instead prove that our notion has the same properties as Joyce’s and is just as useful. (Of course, the counting invariants we obtain are the same as the ones obtained by Joyce: the formula
$\mathfrak{M}=\mathfrak{Vect}$
, see the appendix), but instead prove that our notion has the same properties as Joyce’s and is just as useful. (Of course, the counting invariants we obtain are the same as the ones obtained by Joyce: the formula
![]() $\int _{q=1}\log _{\ast }(1+[\mathfrak{N}])$
, see (39), does not involve explicitly the definition of virtually indecomposable object.)
$\int _{q=1}\log _{\ast }(1+[\mathfrak{N}])$
, see (39), does not involve explicitly the definition of virtually indecomposable object.)
We think of the Lie algebra
![]() $K^{\text{vir}}(\mathfrak{M})$
as an analogue of the Lie algebra of primitive elements in a cocommutative Hopf algebra. In fact, one may ask whether
$K^{\text{vir}}(\mathfrak{M})$
as an analogue of the Lie algebra of primitive elements in a cocommutative Hopf algebra. In fact, one may ask whether
![]() $(K(\mathfrak{M}),\ast )$
is equal to the universal enveloping algebra of the Lie algebra
$(K(\mathfrak{M}),\ast )$
is equal to the universal enveloping algebra of the Lie algebra
![]() $K^{\text{vir}}(\mathfrak{M})$
. To deduce such a statement from structure theorems for Hopf algebras, one would need to enhance
$K^{\text{vir}}(\mathfrak{M})$
. To deduce such a statement from structure theorems for Hopf algebras, one would need to enhance
![]() $K(\mathfrak{M})$
to a cocommutative Hopf algebra. We have not been able to construct the necessary coproduct. We view the family of operators
$K(\mathfrak{M})$
to a cocommutative Hopf algebra. We have not been able to construct the necessary coproduct. We view the family of operators
![]() $(E_{n})$
as something of a replacement. It lets us prove at least some of the results expected of a cocommutative Hopf algebra, in particular Theorems 3 and 4.
$(E_{n})$
as something of a replacement. It lets us prove at least some of the results expected of a cocommutative Hopf algebra, in particular Theorems 3 and 4.
1 Linear algebraic stacks and algebroids
1.1 Algebraic stacks
Let us briefly summarize our conventions about algebraic stacks.
We choose a noetherian base ring
![]() $R$
(commutative and with unit), and we fix our base category
$R$
(commutative and with unit), and we fix our base category
![]() $\mathscr{S}$
to be the category of
$\mathscr{S}$
to be the category of
![]() $R$
-schemes, endowed with the étale topology. Over
$R$
-schemes, endowed with the étale topology. Over
![]() $\mathscr{S}$
we have a canonical sheaf of
$\mathscr{S}$
we have a canonical sheaf of
![]() $R$
-algebras
$R$
-algebras
![]() $\mathscr{O}_{\mathscr{S}}$
; it is represented by
$\mathscr{O}_{\mathscr{S}}$
; it is represented by
![]() $\mathbb{A}^{1}=\mathbb{A}_{\operatorname{Spec}R}^{1}$
and called the structure sheaf.
$\mathbb{A}^{1}=\mathbb{A}_{\operatorname{Spec}R}^{1}$
and called the structure sheaf.
We will assume our algebraic stacks to be locally of finite type. Thus, an algebraic stack is a stack over the site
![]() $\mathscr{S}$
that admits a presentation by a groupoid
$\mathscr{S}$
that admits a presentation by a groupoid
![]() $X_{1}\rightrightarrows X_{0}$
, where
$X_{1}\rightrightarrows X_{0}$
, where
![]() $X_{0}$
and
$X_{0}$
and
![]() $X_{1}$
are algebraic spaces, locally of finite type over
$X_{1}$
are algebraic spaces, locally of finite type over
![]() $R$
, the source and target morphisms
$R$
, the source and target morphisms
![]() $s,t:X_{1}\rightarrow X_{0}$
are smooth, and the diagonal
$s,t:X_{1}\rightarrow X_{0}$
are smooth, and the diagonal
![]() $X_{1}\rightarrow X_{0}\times X_{0}$
is of finite type. In fact, all algebraic stacks we encounter will have affine diagonal.
$X_{1}\rightarrow X_{0}\times X_{0}$
is of finite type. In fact, all algebraic stacks we encounter will have affine diagonal.
By a stratification of an algebraic stack
![]() $X$
, we mean a morphism of algebraic stacks
$X$
, we mean a morphism of algebraic stacks
![]() $X^{\prime }\rightarrow X$
that is a surjective monomorphism and that admits a finite decomposition
$X^{\prime }\rightarrow X$
that is a surjective monomorphism and that admits a finite decomposition
![]() $X^{\prime }=\coprod _{i}X_{i}$
such that every
$X^{\prime }=\coprod _{i}X_{i}$
such that every
![]() $X_{i}\rightarrow X$
is a locally closed embedding of algebraic stacks.
$X_{i}\rightarrow X$
is a locally closed embedding of algebraic stacks.
If
![]() $G$
is an algebraic group acting on the algebraic space
$G$
is an algebraic group acting on the algebraic space
![]() $X$
, we will denote the quotient stack by
$X$
, we will denote the quotient stack by
![]() $X/G$
, because we fear the more common notation
$X/G$
, because we fear the more common notation
![]() $[X/G]$
would lead to confusion with the notation for elements of various
$[X/G]$
would lead to confusion with the notation for elements of various
![]() $K$
-groups of schemes and stacks.
$K$
-groups of schemes and stacks.
Suppose
![]() $G\rightarrow X$
is a relative group scheme over the stack
$G\rightarrow X$
is a relative group scheme over the stack
![]() $X$
. The connected component of
$X$
. The connected component of
![]() $G$
, denoted by
$G$
, denoted by
![]() $G^{\circ }$
, is the subsheaf of
$G^{\circ }$
, is the subsheaf of
![]() $G$
defined by requiring a section
$G$
defined by requiring a section
![]() $g\in G(S)$
to factor through
$g\in G(S)$
to factor through
![]() $G^{\circ }(S)$
if and only if for all points (equivalently geometric points)
$G^{\circ }(S)$
if and only if for all points (equivalently geometric points)
![]() $s$
of
$s$
of
![]() $S$
, we have
$S$
, we have
![]() $g(s)\in G_{s}^{\circ }$
. If
$g(s)\in G_{s}^{\circ }$
. If
![]() $G\rightarrow X$
is smooth, the connected component
$G\rightarrow X$
is smooth, the connected component
![]() $G^{\circ }\subset G$
is represented by an open substack of
$G^{\circ }\subset G$
is represented by an open substack of
![]() $G$
, which is a smooth group scheme with geometrically connected fibres over
$G$
, which is a smooth group scheme with geometrically connected fibres over
![]() $X$
. (See [Reference Artin, Bertin, Demazure, Grothendieck, Gabriel, Raynaud and SerreSGA3, Exposé VI
$X$
. (See [Reference Artin, Bertin, Demazure, Grothendieck, Gabriel, Raynaud and SerreSGA3, Exposé VI
![]() $_{\text{B}}$
, Théoreme 3.10].)
$_{\text{B}}$
, Théoreme 3.10].)
If the inertia stack
![]() $I_{X}$
of an algebraic stack
$I_{X}$
of an algebraic stack
![]() $X$
is smooth over
$X$
is smooth over
![]() $X$
, the connected component
$X$
, the connected component
![]() $I_{X}^{\circ }$
is an algebraic stack. We can apply the rigidification construction (see, for example, [Reference Abramovich, Olsson and VistoliAOV08, Appendix]) to
$I_{X}^{\circ }$
is an algebraic stack. We can apply the rigidification construction (see, for example, [Reference Abramovich, Olsson and VistoliAOV08, Appendix]) to
![]() $I_{X}^{\circ }\subset I_{X}$
and obtain a (uniquely determined) Deligne–Mumford stack
$I_{X}^{\circ }\subset I_{X}$
and obtain a (uniquely determined) Deligne–Mumford stack
![]() $\overline{X}$
, together with a morphism
$\overline{X}$
, together with a morphism
![]() $X\rightarrow \overline{X}$
, making
$X\rightarrow \overline{X}$
, making
![]() $X$
a connected gerbe over
$X$
a connected gerbe over
![]() $\overline{X}$
(which means that the relative inertia of
$\overline{X}$
(which means that the relative inertia of
![]() $X$
over
$X$
over
![]() $\overline{X}$
has connected fibres). The structure morphism
$\overline{X}$
has connected fibres). The structure morphism
![]() $X\rightarrow \overline{X}$
is smooth.
$X\rightarrow \overline{X}$
is smooth.
A gerbe
![]() $X\rightarrow \overline{X}$
is an isotrivial gerbe if it admits a section over a finite étale
$X\rightarrow \overline{X}$
is an isotrivial gerbe if it admits a section over a finite étale
![]() $\overline{X}$
-stack. If
$\overline{X}$
-stack. If
![]() $X\rightarrow \overline{X}$
is a smooth gerbe over a Deligne–Mumford stack, there exists a stratification
$X\rightarrow \overline{X}$
is a smooth gerbe over a Deligne–Mumford stack, there exists a stratification
![]() $\overline{X}^{\prime }\rightarrow \overline{X}$
such that the restriction of the gerbe
$\overline{X}^{\prime }\rightarrow \overline{X}$
such that the restriction of the gerbe
![]() $X$
to
$X$
to
![]() $\overline{X}^{\prime }$
is isotrivial. (This follows from the fact that a quasi-finite morphism of Deligne–Mumford stacks is generically finite. This, in turn, follows from Zariski’s main theorem [Reference Laumon and Moret-BaillyLMB00, §16].)
$\overline{X}^{\prime }$
is isotrivial. (This follows from the fact that a quasi-finite morphism of Deligne–Mumford stacks is generically finite. This, in turn, follows from Zariski’s main theorem [Reference Laumon and Moret-BaillyLMB00, §16].)
Let us also remark that every Deligne–Mumford stack admits a stratification by integral normal Deligne–Mumford stacks, although we do not use this fact.
Sheaves on algebraic stacks
We need to clarify the notions of vector bundle, coherent sheaf, and representable sheaf of
![]() $\mathscr{O}_{X}$
-modules, and how they relate to each other.
$\mathscr{O}_{X}$
-modules, and how they relate to each other.
An algebraic stack
![]() $X$
is a fibred category
$X$
is a fibred category
![]() $X\rightarrow \mathscr{S}$
. The category
$X\rightarrow \mathscr{S}$
. The category
![]() $X$
inherits a topology from
$X$
inherits a topology from
![]() $\mathscr{S}$
, called the étale topology, and
$\mathscr{S}$
, called the étale topology, and
![]() $X$
endowed with this topology is the big étale site of
$X$
endowed with this topology is the big étale site of
![]() $X$
. Sheaves over
$X$
. Sheaves over
![]() $X$
are by definition sheaves on this big étale site. For example,
$X$
are by definition sheaves on this big étale site. For example,
![]() $\mathscr{O}_{\mathscr{S}}$
induces a sheaf of
$\mathscr{O}_{\mathscr{S}}$
induces a sheaf of
![]() $R$
-algebras on
$R$
-algebras on
![]() $X$
, which is denoted by
$X$
, which is denoted by
![]() $\mathscr{O}_{X}$
and called the structure sheaf of
$\mathscr{O}_{X}$
and called the structure sheaf of
![]() $X$
. It is represented by
$X$
. It is represented by
![]() $\mathbb{A}_{X}^{1}$
.
$\mathbb{A}_{X}^{1}$
.
A sheaf
![]() $\mathscr{F}$
over
$\mathscr{F}$
over
![]() $X$
induces, for every object
$X$
induces, for every object
![]() $x$
of
$x$
of
![]() $X$
lying over the object
$X$
lying over the object
![]() $U$
of
$U$
of
![]() $\mathscr{S}$
, a sheaf on the usual (small) étale site
$\mathscr{S}$
, a sheaf on the usual (small) étale site
![]() $U_{\acute{\text{e}}\text{t}}$
of the scheme
$U_{\acute{\text{e}}\text{t}}$
of the scheme
![]() $U$
, denoted
$U$
, denoted
![]() $\mathscr{F}_{U}$
. Moreover, for every morphism
$\mathscr{F}_{U}$
. Moreover, for every morphism
![]() $\unicode[STIX]{x1D6FC}:y\rightarrow x$
lying over
$\unicode[STIX]{x1D6FC}:y\rightarrow x$
lying over
![]() $f:V\rightarrow U$
, we obtain a morphism of sheaves
$f:V\rightarrow U$
, we obtain a morphism of sheaves
![]() $\unicode[STIX]{x1D6FC}^{\ast }:f^{-1}(\mathscr{F}_{U})\rightarrow \mathscr{F}_{V}$
. (The
$\unicode[STIX]{x1D6FC}^{\ast }:f^{-1}(\mathscr{F}_{U})\rightarrow \mathscr{F}_{V}$
. (The
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
satisfy an obvious cocycle condition and the condition that they are isomorphisms if
$\unicode[STIX]{x1D6FC}^{\ast }$
satisfy an obvious cocycle condition and the condition that they are isomorphisms if
![]() $f$
is étale.) For example, the structure sheaf
$f$
is étale.) For example, the structure sheaf
![]() $\mathscr{O}_{X}$
induces the structure sheaf on
$\mathscr{O}_{X}$
induces the structure sheaf on
![]() $U_{\acute{\text{e}}\text{t}}$
, for every such
$U_{\acute{\text{e}}\text{t}}$
, for every such
![]() $x/U$
. The data of the small étale sheaves
$x/U$
. The data of the small étale sheaves
![]() $\mathscr{F}_{U}$
, together with the compatibility morphisms
$\mathscr{F}_{U}$
, together with the compatibility morphisms
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
, satisfying the two parenthetical conditions, is equivalent to the data defining
$\unicode[STIX]{x1D6FC}^{\ast }$
, satisfying the two parenthetical conditions, is equivalent to the data defining
![]() $\mathscr{F}$
(see [Reference Artin, Grothendieck and VerdierSGA4, Exp. IV, 4.10]). The functor
$\mathscr{F}$
(see [Reference Artin, Grothendieck and VerdierSGA4, Exp. IV, 4.10]). The functor
![]() $\mathscr{F}\mapsto \mathscr{F}_{U}$
is the sheaf pullback morphism of a morphism of sites
$\mathscr{F}\mapsto \mathscr{F}_{U}$
is the sheaf pullback morphism of a morphism of sites
![]() $U_{\acute{\text{e}}\text{t}}\rightarrow X$
, from the small étale site of
$U_{\acute{\text{e}}\text{t}}\rightarrow X$
, from the small étale site of
![]() $U$
to the big étale site of
$U$
to the big étale site of
![]() $X$
. In particular,
$X$
. In particular,
![]() $\mathscr{F}\mapsto \mathscr{F}_{U}$
is exact. Both
$\mathscr{F}\mapsto \mathscr{F}_{U}$
is exact. Both
![]() $U_{\acute{\text{e}}\text{t}}$
and
$U_{\acute{\text{e}}\text{t}}$
and
![]() $X$
are ringed sites, and
$X$
are ringed sites, and
![]() $\mathscr{F}\mapsto \mathscr{F}_{U}$
is also the sheaf of modules pullback of the morphism of ringed sites
$\mathscr{F}\mapsto \mathscr{F}_{U}$
is also the sheaf of modules pullback of the morphism of ringed sites
![]() $U_{\acute{\text{e}}\text{t}}\rightarrow X$
. Therefore, the functor
$U_{\acute{\text{e}}\text{t}}\rightarrow X$
. Therefore, the functor
![]() $\mathscr{F}\rightarrow \mathscr{F}_{U}$
is also exact when considered as a functor from the category of big sheaves of
$\mathscr{F}\rightarrow \mathscr{F}_{U}$
is also exact when considered as a functor from the category of big sheaves of
![]() $\mathscr{O}_{X}$
-modules to the category of small sheaves of
$\mathscr{O}_{X}$
-modules to the category of small sheaves of
![]() $\mathscr{O}_{U_{\acute{\text{e}}\text{t}}}$
-modules.
$\mathscr{O}_{U_{\acute{\text{e}}\text{t}}}$
-modules.
If
![]() $\mathscr{F}$
and
$\mathscr{F}$
and
![]() $\mathscr{G}$
are sheaves of
$\mathscr{G}$
are sheaves of
![]() $\mathscr{O}_{X}$
-modules, then
$\mathscr{O}_{X}$
-modules, then
![]() $\mathscr{H}om(\mathscr{F},\mathscr{G})$
is again a sheaf of
$\mathscr{H}om(\mathscr{F},\mathscr{G})$
is again a sheaf of
![]() $\mathscr{O}_{X}$
-modules. In particular, for a sheaf of
$\mathscr{O}_{X}$
-modules. In particular, for a sheaf of
![]() $\mathscr{O}_{X}$
-modules, we have the dual
$\mathscr{O}_{X}$
-modules, we have the dual
![]() $\mathscr{F}^{\vee }=\mathscr{H}om(\mathscr{F},\mathscr{O}_{X})$
.
$\mathscr{F}^{\vee }=\mathscr{H}om(\mathscr{F},\mathscr{O}_{X})$
.
Note that, in general, the natural homomorphism
![]() $\mathscr{H}om(\mathscr{F},\mathscr{G})_{U}\rightarrow \mathscr{H}om(\mathscr{F}_{U},\mathscr{G}_{U})$
is not an isomorphism; see Example 1.6.
$\mathscr{H}om(\mathscr{F},\mathscr{G})_{U}\rightarrow \mathscr{H}om(\mathscr{F}_{U},\mathscr{G}_{U})$
is not an isomorphism; see Example 1.6.
Coherent sheaves
A sheaf
![]() $\mathscr{F}$
of
$\mathscr{F}$
of
![]() $\mathscr{O}_{X}$
-modules is locally coherent if for every
$\mathscr{O}_{X}$
-modules is locally coherent if for every
![]() $x/U$
, the sheaf
$x/U$
, the sheaf
![]() $\mathscr{F}_{U}$
is a coherent sheaf of
$\mathscr{F}_{U}$
is a coherent sheaf of
![]() $\mathscr{O}_{U_{\acute{\text{e}}\text{t}}}$
-modules. (This terminology is inspired by [Sta15, Tag 06WJ].) It is cartesian if all compatibility morphisms
$\mathscr{O}_{U_{\acute{\text{e}}\text{t}}}$
-modules. (This terminology is inspired by [Sta15, Tag 06WJ].) It is cartesian if all compatibility morphisms
![]() $\unicode[STIX]{x1D6FC}^{\ast }:f^{\ast }\mathscr{F}_{U}\rightarrow \mathscr{F}_{V}$
are isomorphisms of sheaves of
$\unicode[STIX]{x1D6FC}^{\ast }:f^{\ast }\mathscr{F}_{U}\rightarrow \mathscr{F}_{V}$
are isomorphisms of sheaves of
![]() $\mathscr{O}_{V_{\acute{\text{e}}\text{t}}}$
-modules. A sheaf that is both locally coherent and cartesian is coherent. The coherent sheaf
$\mathscr{O}_{V_{\acute{\text{e}}\text{t}}}$
-modules. A sheaf that is both locally coherent and cartesian is coherent. The coherent sheaf
![]() $\mathscr{F}$
is said to be locally free coherent if every
$\mathscr{F}$
is said to be locally free coherent if every
![]() $\mathscr{F}_{U}$
is locally free. (This is equivalent to
$\mathscr{F}_{U}$
is locally free. (This is equivalent to
![]() $\mathscr{F}$
being locally free.)
$\mathscr{F}$
being locally free.)
For example, a groupoid presentation
![]() $X_{1}\rightrightarrows X_{0}$
of
$X_{1}\rightrightarrows X_{0}$
of
![]() $X$
and a coherent sheaf
$X$
and a coherent sheaf
![]() $\mathscr{F}_{0}$
on
$\mathscr{F}_{0}$
on
![]() $X_{0}$
, together with an isomorphism
$X_{0}$
, together with an isomorphism
![]() $s^{\ast }\mathscr{F}_{0}\rightarrow t^{\ast }\mathscr{F}_{0}$
, satisfying the usual cocycle condition on
$s^{\ast }\mathscr{F}_{0}\rightarrow t^{\ast }\mathscr{F}_{0}$
, satisfying the usual cocycle condition on
![]() $X_{2}=X_{1}\times _{X_{0}}X_{1}$
, give rise to a coherent sheaf
$X_{2}=X_{1}\times _{X_{0}}X_{1}$
, give rise to a coherent sheaf
![]() $\mathscr{F}$
on
$\mathscr{F}$
on
![]() $X$
. If
$X$
. If
![]() $\mathscr{F}_{0}$
is locally free, then
$\mathscr{F}_{0}$
is locally free, then
![]() $\mathscr{F}$
is locally free.
$\mathscr{F}$
is locally free.
A vector bundle over
![]() $X$
is a representable morphism
$X$
is a representable morphism
![]() $E\rightarrow X$
endowed with an addition operation and a compatible
$E\rightarrow X$
endowed with an addition operation and a compatible
![]() $\mathbb{G}_{m}$
-action such that the pullback of
$\mathbb{G}_{m}$
-action such that the pullback of
![]() $E\rightarrow X$
to any scheme
$E\rightarrow X$
to any scheme
![]() $U\rightarrow X$
is a vector bundle on
$U\rightarrow X$
is a vector bundle on
![]() $U$
.
$U$
.
The sheaf of sections of a vector bundle over
![]() $X$
is a coherent sheaf. In fact, the notions of vector bundle and locally free coherent sheaf are equivalent, and we will use them interchangeably. (The inverse functor is given by
$X$
is a coherent sheaf. In fact, the notions of vector bundle and locally free coherent sheaf are equivalent, and we will use them interchangeably. (The inverse functor is given by
![]() $\mathscr{E}\mapsto \operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{E}^{\vee }$
.) The cokernel of a homomorphism of vector bundles is coherent. In fact, every cokernel of a homomorphism of coherent sheaves is coherent.
$\mathscr{E}\mapsto \operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{E}^{\vee }$
.) The cokernel of a homomorphism of vector bundles is coherent. In fact, every cokernel of a homomorphism of coherent sheaves is coherent.
If the cokernel of a homomorphism of vector bundles is locally free, we call the homomorphism a strict homomorphism of vector bundles. For a strict homomorphism of vector bundles, the image and the kernel, as well as the cokernel, are locally free.
A strict monomorphism of vector bundles is a strict homomorphism whose kernel is zero. A homomorphism of vector bundles is a strict monomorphism/an epimorphism if and only if over every geometric point of
![]() $X$
, the induced linear map is injective/surjective. A homomorphism of vector bundles, which is a monomorphism of sheaves, is a strict monomorphism of bundles.
$X$
, the induced linear map is injective/surjective. A homomorphism of vector bundles, which is a monomorphism of sheaves, is a strict monomorphism of bundles.
Let
![]() $\unicode[STIX]{x1D711}:E\rightarrow F$
be a homomorphism of vector bundles over the algebraic stack
$\unicode[STIX]{x1D711}:E\rightarrow F$
be a homomorphism of vector bundles over the algebraic stack
![]() $X$
. The flattening stratification
$X$
. The flattening stratification
![]() $X^{\prime }\rightarrow X$
of
$X^{\prime }\rightarrow X$
of
![]() $\operatorname{cok}\unicode[STIX]{x1D711}$
serves also as a strictening stratification for
$\operatorname{cok}\unicode[STIX]{x1D711}$
serves also as a strictening stratification for
![]() $\unicode[STIX]{x1D711}$
. This means that an object of
$\unicode[STIX]{x1D711}$
. This means that an object of
![]() $X(S)$
lifts to
$X(S)$
lifts to
![]() $X^{\prime }(S)$
if and only if
$X^{\prime }(S)$
if and only if
![]() $\unicode[STIX]{x1D711}_{S}$
is strict.
$\unicode[STIX]{x1D711}_{S}$
is strict.
In general, the kernel (in the category of big sheaves of
![]() $\mathscr{O}_{X}$
-modules) of a homomorphism of vector bundles is locally coherent, but not coherent.
$\mathscr{O}_{X}$
-modules) of a homomorphism of vector bundles is locally coherent, but not coherent.
By [Sta15, Tag 06WK], a sheaf of
![]() $\mathscr{O}_{X}$
-modules
$\mathscr{O}_{X}$
-modules
![]() $\mathscr{F}$
is coherent if and only if there exists a smooth covering
$\mathscr{F}$
is coherent if and only if there exists a smooth covering
![]() $X_{i}\rightarrow X$
of
$X_{i}\rightarrow X$
of
![]() $X$
by finite type affine schemes
$X$
by finite type affine schemes
![]() $X_{i}$
such that for every
$X_{i}$
such that for every
![]() $i$
, the restriction
$i$
, the restriction
![]() $\mathscr{F}_{i}$
of
$\mathscr{F}_{i}$
of
![]() $\mathscr{F}$
to the big étale site of
$\mathscr{F}$
to the big étale site of
![]() $X_{i}$
is isomorphic to the cokernel of a homomorphism of vector bundles.
$X_{i}$
is isomorphic to the cokernel of a homomorphism of vector bundles.
Proposition 1.1. Suppose that
![]() $\mathscr{F}$
is a coherent sheaf on the algebraic stack
$\mathscr{F}$
is a coherent sheaf on the algebraic stack
![]() $X$
. Then:
$X$
. Then:
(i) for every
 $x/U$
, we have
$x/U$
, we have
 $(\mathscr{F}^{\vee })_{U}=(\mathscr{F}_{U})^{\vee }$
;
$(\mathscr{F}^{\vee })_{U}=(\mathscr{F}_{U})^{\vee }$
;(ii)
 $\mathscr{F}^{\vee }$
is locally coherent;
$\mathscr{F}^{\vee }$
is locally coherent;(iii)
 $\mathscr{F}^{\vee }$
is represented by a an algebraic stack, which is of finite type and affine over
$\mathscr{F}^{\vee }$
is represented by a an algebraic stack, which is of finite type and affine over
 $X$
, namely,
$X$
, namely,
 $\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
;
$\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
;(iv) the canonical homomorphism
 $\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism of sheaves of
$\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism of sheaves of
 $\mathscr{O}_{X}$
-modules;
$\mathscr{O}_{X}$
-modules;(v) if
 $\mathscr{F}$
is locally free coherent, then
$\mathscr{F}$
is locally free coherent, then
 $\mathscr{F}^{\vee }$
is a vector bundle.
$\mathscr{F}^{\vee }$
is a vector bundle.
Moreover, the functor
![]() $\mathscr{F}\mapsto \mathscr{F}^{\vee }$
is a fully faithful functor from the category of coherent sheaves to the category of locally coherent sheaves of
$\mathscr{F}\mapsto \mathscr{F}^{\vee }$
is a fully faithful functor from the category of coherent sheaves to the category of locally coherent sheaves of
![]() $\mathscr{O}_{X}$
-modules. It maps right exact sequences of coherent sheaves to left exact sequences of locally coherent sheaves.
$\mathscr{O}_{X}$
-modules. It maps right exact sequences of coherent sheaves to left exact sequences of locally coherent sheaves.
Proof. The canonical homomorphism
![]() $\mathscr{H}om(\mathscr{F},\mathscr{G})_{U}\rightarrow \mathscr{H}om(\mathscr{F}_{U},\mathscr{G}_{U})$
is an isomorphism for all
$\mathscr{H}om(\mathscr{F},\mathscr{G})_{U}\rightarrow \mathscr{H}om(\mathscr{F}_{U},\mathscr{G}_{U})$
is an isomorphism for all
![]() $U$
in
$U$
in
![]() $\mathscr{S}$
, if
$\mathscr{S}$
, if
![]() $\mathscr{F}$
is cartesian. This implies the first claim.
$\mathscr{F}$
is cartesian. This implies the first claim.
The second claim follows from the first (see also [Sta15, Tag 06WM]).
For the third claim, see [Reference Laumon and Moret-BaillyLMB00, (14.2.6)].
For the fourth claim, notice that both
![]() $\mathscr{F}^{\vee }$
and
$\mathscr{F}^{\vee }$
and
![]() $\mathscr{O}_{X}$
are representable and affine over
$\mathscr{O}_{X}$
are representable and affine over
![]() $X$
, namely,
$X$
, namely,
![]() $\mathscr{F}^{\vee }=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
and
$\mathscr{F}^{\vee }=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
and
![]() $\mathscr{O}_{X}=\mathbb{A}_{X}^{1}$
. They are also both endowed with
$\mathscr{O}_{X}=\mathbb{A}_{X}^{1}$
. They are also both endowed with
![]() $\mathbb{G}_{m}$
-actions, via scalar multiplication. We consider the big sheaf of
$\mathbb{G}_{m}$
-actions, via scalar multiplication. We consider the big sheaf of
![]() $\mathbb{G}_{m}$
-equivariant
$\mathbb{G}_{m}$
-equivariant
![]() $X$
-morphisms from
$X$
-morphisms from
![]() $\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
to
$\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
to
![]() $\mathbb{A}_{X}^{1}$
, denoted by
$\mathbb{A}_{X}^{1}$
, denoted by
![]() $\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
. The sections of
$\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
. The sections of
![]() $\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
over
$\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
over
![]() $S\rightarrow X$
are the
$S\rightarrow X$
are the
![]() $\mathbb{G}_{m}$
-equivariant
$\mathbb{G}_{m}$
-equivariant
![]() $S$
-morphisms
$S$
-morphisms
![]() $\operatorname{Spec}_{S}\operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}\rightarrow \mathbb{A}_{S}^{1}$
or, equivalently, the morphisms of sheaves of
$\operatorname{Spec}_{S}\operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}\rightarrow \mathbb{A}_{S}^{1}$
or, equivalently, the morphisms of sheaves of
![]() $\mathscr{O}_{S}$
-algebras
$\mathscr{O}_{S}$
-algebras
![]() $\mathscr{O}_{S}[t]\rightarrow \operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}$
of degree 1. These are the same as the sections of
$\mathscr{O}_{S}[t]\rightarrow \operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}$
of degree 1. These are the same as the sections of
![]() $\mathscr{F}_{S}$
over
$\mathscr{F}_{S}$
over
![]() $S$
. This proves that
$S$
. This proves that
![]() $\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})=\mathscr{F}$
.
$\operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})=\mathscr{F}$
.
On the other hand, the sections of
![]() $\mathscr{H}om(\mathscr{F}^{\vee },\mathscr{O})$
over
$\mathscr{H}om(\mathscr{F}^{\vee },\mathscr{O})$
over
![]() $S\rightarrow X$
are the
$S\rightarrow X$
are the
![]() $\mathscr{O}$
-linear homomorphisms
$\mathscr{O}$
-linear homomorphisms
![]() $\operatorname{Spec}_{S}\operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}\rightarrow \mathbb{A}_{S}^{1}$
, which are, in particular,
$\operatorname{Spec}_{S}\operatorname{Sym}_{\mathscr{O}_{S}}\mathscr{F}_{S}\rightarrow \mathbb{A}_{S}^{1}$
, which are, in particular,
![]() $\mathbb{G}_{m}$
-equivariant. Thus we have a natural map
$\mathbb{G}_{m}$
-equivariant. Thus we have a natural map
![]() $\mathscr{H}om(F^{\vee },\mathscr{O})\rightarrow \operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
. In total, we have a canonical map
$\mathscr{H}om(F^{\vee },\mathscr{O})\rightarrow \operatorname{Hom̲}_{\mathbb{G}_{m}}(\mathscr{F}^{\vee },\mathbb{A}^{1})$
. In total, we have a canonical map
which is inverse to the tautological map
![]() $\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
.
$\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
.
The fifth claim is clear.
The ‘moreover’ follows from the fact that we can reconstruct
![]() $\mathscr{F}$
from
$\mathscr{F}$
from
![]() $\mathscr{F}^{\vee }=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
, as the degree 1 part of the graded sheaf of
$\mathscr{F}^{\vee }=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
, as the degree 1 part of the graded sheaf of
![]() $\mathscr{O}_{X}$
-modules
$\mathscr{O}_{X}$
-modules
![]() $\unicode[STIX]{x1D70B}_{\ast }(\mathscr{O}_{\mathscr{F}^{\vee }})$
, where
$\unicode[STIX]{x1D70B}_{\ast }(\mathscr{O}_{\mathscr{F}^{\vee }})$
, where
![]() $\unicode[STIX]{x1D70B}:\mathscr{F}^{\vee }\rightarrow X$
is the projection morphism.◻
$\unicode[STIX]{x1D70B}:\mathscr{F}^{\vee }\rightarrow X$
is the projection morphism.◻
Representable sheaves of modules
If
![]() $\unicode[STIX]{x1D711}:E\rightarrow F$
is a homomorphism of vector bundles over
$\unicode[STIX]{x1D711}:E\rightarrow F$
is a homomorphism of vector bundles over
![]() $X$
, then
$X$
, then
![]() $\ker \unicode[STIX]{x1D711}$
, constructed in the category of big sheaves, is a representable sheaf of
$\ker \unicode[STIX]{x1D711}$
, constructed in the category of big sheaves, is a representable sheaf of
![]() $\mathscr{O}_{X}$
-modules. In fact,
$\mathscr{O}_{X}$
-modules. In fact,
![]() $\ker \unicode[STIX]{x1D711}$
is equal to the fibred product of stacks as shown in the following diagram.
$\ker \unicode[STIX]{x1D711}$
is equal to the fibred product of stacks as shown in the following diagram.

Sheaves such as
![]() $\ker \unicode[STIX]{x1D711}$
belong to a class of
$\ker \unicode[STIX]{x1D711}$
belong to a class of
![]() $\mathscr{O}_{X}$
-modules dual to coherent sheaves.
$\mathscr{O}_{X}$
-modules dual to coherent sheaves.
Proposition 1.2. Let
![]() $\mathscr{F}$
be a sheaf of
$\mathscr{F}$
be a sheaf of
![]() $\mathscr{O}_{X}$
-modules. The following are equivalent.
$\mathscr{O}_{X}$
-modules. The following are equivalent.
(i) There exists a coherent sheaf
 $\mathscr{N}$
such that
$\mathscr{N}$
such that
 $\mathscr{F}$
is isomorphic to
$\mathscr{F}$
is isomorphic to
 $\mathscr{N}^{\vee }$
.
$\mathscr{N}^{\vee }$
.(ii) There exists a smooth cover
 $X_{i}\rightarrow X$
of
$X_{i}\rightarrow X$
of
 $X$
by finite type affine schemes
$X$
by finite type affine schemes
 $X_{i}$
such that, for every
$X_{i}$
such that, for every
 $i$
, the restriction
$i$
, the restriction
 $\mathscr{F}_{i}$
of
$\mathscr{F}_{i}$
of
 $\mathscr{F}$
to the big étale site of
$\mathscr{F}$
to the big étale site of
 $X_{i}$
is isomorphic to the kernel of a homomorphism of vector bundles over
$X_{i}$
is isomorphic to the kernel of a homomorphism of vector bundles over
 $X_{i}$
.
$X_{i}$
.
Proof. The fact that (i) implies (ii) follows from the results proved above. So let us indicate how to prove that (ii) implies (i).
Let us first assume that
![]() $\mathscr{F}$
is isomorphic to the kernel of a homomorphism of vector bundles
$\mathscr{F}$
is isomorphic to the kernel of a homomorphism of vector bundles
![]() $E_{0}\rightarrow E_{1}$
. One checks that
$E_{0}\rightarrow E_{1}$
. One checks that
![]() $\mathscr{F}$
is then represented by
$\mathscr{F}$
is then represented by
![]() $\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\operatorname{cok}(E_{1}^{\vee }\rightarrow E_{0}^{\vee })$
. Thus,
$\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\operatorname{cok}(E_{1}^{\vee }\rightarrow E_{0}^{\vee })$
. Thus,
![]() $\mathscr{F}$
is isomorphic to the dual of the coherent sheaf
$\mathscr{F}$
is isomorphic to the dual of the coherent sheaf
![]() $\operatorname{cok}(E_{1}^{\vee }\rightarrow E_{0}^{\vee })$
.
$\operatorname{cok}(E_{1}^{\vee }\rightarrow E_{0}^{\vee })$
.
Now suppose that
![]() $\mathscr{F}$
is locally isomorphic to the kernel of a homomorphism of vector bundles. It suffices to prove that
$\mathscr{F}$
is locally isomorphic to the kernel of a homomorphism of vector bundles. It suffices to prove that
![]() $\mathscr{F}^{\vee }$
is coherent and that
$\mathscr{F}^{\vee }$
is coherent and that
![]() $\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism. Both claims can be checked locally and are true for duals of coherent sheaves.◻
$\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism. Both claims can be checked locally and are true for duals of coherent sheaves.◻
Definition 1.3. We say a sheaf of
![]() $\mathscr{O}_{X}$
-modules is locally coherent representable if any of the two equivalent conditions of Proposition 1.2 is satisfied. The terminology is justified by Proposition 1.4 below.
$\mathscr{O}_{X}$
-modules is locally coherent representable if any of the two equivalent conditions of Proposition 1.2 is satisfied. The terminology is justified by Proposition 1.4 below.
In other words, the category of locally coherent representable sheaves over
![]() $X$
is the essential image of the fully faithful functor mentioned in Proposition 1.1. We therefore have an equivalence of categories
$X$
is the essential image of the fully faithful functor mentioned in Proposition 1.1. We therefore have an equivalence of categories
The following proposition summarizes facts about locally coherent representable sheaves, which all follow easily from facts mentioned above.
Proposition 1.4. Let
![]() $\mathscr{F}$
be a locally coherent representable sheaf over the algebraic stack
$\mathscr{F}$
be a locally coherent representable sheaf over the algebraic stack
![]() $X$
. Then:
$X$
. Then:
(i) the sheaf
 $\mathscr{F}$
is locally coherent;
$\mathscr{F}$
is locally coherent;(ii) the sheaf
 $\mathscr{F}^{\vee }$
is coherent;
$\mathscr{F}^{\vee }$
is coherent;(iii) the canonical homomorphism
 $\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism of sheaves of
$\mathscr{F}\rightarrow \mathscr{F}^{\vee \vee }$
is an isomorphism of sheaves of
 $\mathscr{O}_{X}$
-modules;
$\mathscr{O}_{X}$
-modules;(iv) the sheaf
 $\mathscr{F}$
is representable by an algebraic stack
$\mathscr{F}$
is representable by an algebraic stack
 $F\rightarrow X$
, which is of finite type and affine over
$F\rightarrow X$
, which is of finite type and affine over
 $X$
;
$X$
;(v) in fact,
 $\mathscr{F}=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}^{\vee }$
.
$\mathscr{F}=\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}^{\vee }$
.
Moreover, the functor
![]() $\mathscr{F}\mapsto \mathscr{F}^{\vee }$
is an essential inverse to the functor (5). It maps left exact sequences of locally coherent representable sheaves to right exact sequences of coherent sheaves.
$\mathscr{F}\mapsto \mathscr{F}^{\vee }$
is an essential inverse to the functor (5). It maps left exact sequences of locally coherent representable sheaves to right exact sequences of coherent sheaves.
Proposition 1.5. Let
![]() $\mathscr{F}$
be a locally coherent representable sheaf over the finite type algebraic stack
$\mathscr{F}$
be a locally coherent representable sheaf over the finite type algebraic stack
![]() $X$
. There is a unique stratification
$X$
. There is a unique stratification
![]() $X^{\prime }\rightarrow X$
with the property that an
$X^{\prime }\rightarrow X$
with the property that an
![]() $X$
-scheme
$X$
-scheme
![]() $S$
factors through
$S$
factors through
![]() $X^{\prime }$
if and only if
$X^{\prime }$
if and only if
![]() $\mathscr{F}|_{S}$
is a vector bundle. More precisely,
$\mathscr{F}|_{S}$
is a vector bundle. More precisely,
![]() $X^{\prime }=\coprod _{n\geqslant 0}X_{n}$
, and
$X^{\prime }=\coprod _{n\geqslant 0}X_{n}$
, and
![]() $X_{n}\rightarrow X$
is a locally closed immersion of algebraic stacks with the property that
$X_{n}\rightarrow X$
is a locally closed immersion of algebraic stacks with the property that
![]() $S\rightarrow X$
factors through
$S\rightarrow X$
factors through
![]() $X_{n}$
if and only if
$X_{n}$
if and only if
![]() $\mathscr{F}|_{S}$
is a vector bundle of rank
$\mathscr{F}|_{S}$
is a vector bundle of rank
![]() $n$
.
$n$
.
Proof. The sought-after stratification is the flattening stratification of the coherent sheaf
![]() $\mathscr{F}^{\vee }$
.◻
$\mathscr{F}^{\vee }$
.◻
Example 1.6. Consider
![]() $X=\mathbb{A}^{1}$
, with coordinate
$X=\mathbb{A}^{1}$
, with coordinate
![]() $t$
, and let
$t$
, and let
![]() $\mathscr{C}$
be the cokernel of the homomorphism of vector bundles
$\mathscr{C}$
be the cokernel of the homomorphism of vector bundles
![]() $t:\mathbb{A}_{X}^{1}\rightarrow \mathbb{A}_{X}^{1}$
. It is the skyscraper sheaf of the origin, considered as a coherent sheaf on
$t:\mathbb{A}_{X}^{1}\rightarrow \mathbb{A}_{X}^{1}$
. It is the skyscraper sheaf of the origin, considered as a coherent sheaf on
![]() $X$
and extended to a big sheaf over
$X$
and extended to a big sheaf over
![]() $X$
in the usual way. The sheaf
$X$
in the usual way. The sheaf
![]() $\mathscr{C}$
is an example of a coherent sheaf which is not representable.
$\mathscr{C}$
is an example of a coherent sheaf which is not representable.
Let
![]() $\mathscr{K}$
be the kernel of
$\mathscr{K}$
be the kernel of
![]() $t:\mathbb{A}_{X}^{1}\rightarrow \mathbb{A}_{X}^{1}$
. This is locally coherent representable, but not cartesian, and hence not coherent.
$t:\mathbb{A}_{X}^{1}\rightarrow \mathbb{A}_{X}^{1}$
. This is locally coherent representable, but not cartesian, and hence not coherent.
Note that
![]() $\mathscr{C}^{\vee }=\mathscr{K}$
. This shows that
$\mathscr{C}^{\vee }=\mathscr{K}$
. This shows that
![]() $\mathscr{F}^{\vee }$
may not be coherent, even if
$\mathscr{F}^{\vee }$
may not be coherent, even if
![]() $\mathscr{F}$
is.
$\mathscr{F}$
is.
Note also that
![]() $\mathscr{K}^{\vee }=\mathscr{C}$
, which shows that
$\mathscr{K}^{\vee }=\mathscr{C}$
, which shows that
![]() $\mathscr{F}^{\vee }$
may not be representable, even if
$\mathscr{F}^{\vee }$
may not be representable, even if
![]() $\mathscr{F}$
is.
$\mathscr{F}$
is.
Finally, note that
![]() $(\mathscr{K}_{X})^{\vee }=0^{\vee }=0$
, but
$(\mathscr{K}_{X})^{\vee }=0^{\vee }=0$
, but
![]() $(\mathscr{K}^{\vee })_{X}=\mathscr{C}_{X}$
is the structure sheaf of the origin in
$(\mathscr{K}^{\vee })_{X}=\mathscr{C}_{X}$
is the structure sheaf of the origin in
![]() $X$
, considered as a skyscraper sheaf on
$X$
, considered as a skyscraper sheaf on
![]() $X_{\acute{\text{e}}\text{t}}$
, which is not zero. This gives an example where
$X_{\acute{\text{e}}\text{t}}$
, which is not zero. This gives an example where
![]() $(\mathscr{F}^{\vee })_{U}\not =(\mathscr{F}_{U})^{\vee }$
.
$(\mathscr{F}^{\vee })_{U}\not =(\mathscr{F}_{U})^{\vee }$
.
Remark 1.7. Of course, the category of coherent sheaves on an algebraic stack
![]() $X$
has kernels and internal homs, but they do not agree with those in the category of big sheaves, which we considered above. It is therefore important to specify the context when dealing with kernels or duals in the category of coherent sheaves. Unless specified otherwise, we will always consider sheaves of
$X$
has kernels and internal homs, but they do not agree with those in the category of big sheaves, which we considered above. It is therefore important to specify the context when dealing with kernels or duals in the category of coherent sheaves. Unless specified otherwise, we will always consider sheaves of
![]() $\mathscr{O}_{X}$
-modules as big sheaves.
$\mathscr{O}_{X}$
-modules as big sheaves.
1.2 Linear algebraic stacks
We will review the definition of linear algebraic stacks and some basic constructions. For definitions and basic properties of fibred categories we refer the reader to [Reference GrothendieckSGA1, Exposé VI]. The material here is presumably known, but we could not find a suitable reference.
Suppose
![]() $\mathfrak{X}\rightarrow \mathscr{S}$
is a category over
$\mathfrak{X}\rightarrow \mathscr{S}$
is a category over
![]() $\mathscr{S}$
. We write
$\mathscr{S}$
. We write
![]() $\mathfrak{X}(S)$
for the fibre of
$\mathfrak{X}(S)$
for the fibre of
![]() $\mathfrak{X}$
over the object
$\mathfrak{X}$
over the object
![]() $S$
of
$S$
of
![]() $\mathscr{S}$
. If
$\mathscr{S}$
. If
![]() $f:S^{\prime }\rightarrow S$
is a morphism in
$f:S^{\prime }\rightarrow S$
is a morphism in
![]() $\mathscr{S}$
, and
$\mathscr{S}$
, and
![]() $x^{\prime }\in \mathfrak{X}(S^{\prime })$
and
$x^{\prime }\in \mathfrak{X}(S^{\prime })$
and
![]() $x\in \mathfrak{X}(S)$
are
$x\in \mathfrak{X}(S)$
are
![]() $\mathfrak{X}$
-objects lying over
$\mathfrak{X}$
-objects lying over
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $S$
, respectively, we write
$S$
, respectively, we write
![]() $\operatorname{Hom}_{f}(x^{\prime },x)$
for the set of morphisms from
$\operatorname{Hom}_{f}(x^{\prime },x)$
for the set of morphisms from
![]() $x^{\prime }$
to
$x^{\prime }$
to
![]() $x$
in
$x$
in
![]() $\mathfrak{X}$
, lying over
$\mathfrak{X}$
, lying over
![]() $f$
. For
$f$
. For
![]() $S^{\prime }=S$
and
$S^{\prime }=S$
and
![]() $f=\operatorname{id}_{S}$
, we write
$f=\operatorname{id}_{S}$
, we write
![]() $\operatorname{Hom}_{S}(x^{\prime },x)$
.
$\operatorname{Hom}_{S}(x^{\prime },x)$
.
Recall that a morphism
![]() $\unicode[STIX]{x1D6FC}:x^{\prime }\rightarrow x$
lying over
$\unicode[STIX]{x1D6FC}:x^{\prime }\rightarrow x$
lying over
![]() $f:S^{\prime }\rightarrow S$
is cartesian if for every object
$f:S^{\prime }\rightarrow S$
is cartesian if for every object
![]() $x^{\prime \prime }$
of
$x^{\prime \prime }$
of
![]() $\mathfrak{X}(S)$
, composition with
$\mathfrak{X}(S)$
, composition with
![]() $\unicode[STIX]{x1D6FC}$
induces a bijection
$\unicode[STIX]{x1D6FC}$
induces a bijection
![]() $\operatorname{Hom}_{S}(x^{\prime \prime },x^{\prime })\stackrel{\simeq }{\longrightarrow }\operatorname{Hom}_{f}(x^{\prime \prime },x)$
. Recall further that
$\operatorname{Hom}_{S}(x^{\prime \prime },x^{\prime })\stackrel{\simeq }{\longrightarrow }\operatorname{Hom}_{f}(x^{\prime \prime },x)$
. Recall further that
![]() $\mathfrak{X}\rightarrow \mathscr{S}$
is a fibred category if every composition of cartesian morphisms is cartesian and if for every
$\mathfrak{X}\rightarrow \mathscr{S}$
is a fibred category if every composition of cartesian morphisms is cartesian and if for every
![]() $f:S^{\prime }\rightarrow S$
in
$f:S^{\prime }\rightarrow S$
in
![]() $\mathscr{S}$
and every
$\mathscr{S}$
and every
![]() $x$
over
$x$
over
![]() $S$
, there exists a cartesian morphism over
$S$
, there exists a cartesian morphism over
![]() $f$
with target
$f$
with target
![]() $x$
. A cartesian functor between categories over
$x$
. A cartesian functor between categories over
![]() $\mathscr{S}$
is one that preserves cartesian morphisms.
$\mathscr{S}$
is one that preserves cartesian morphisms.
If
![]() $\mathfrak{X}$
is a fibred category over
$\mathfrak{X}$
is a fibred category over
![]() $\mathscr{S}$
, the subcategory of
$\mathscr{S}$
, the subcategory of
![]() $\mathfrak{X}$
consisting of the same objects and all cartesian morphisms is a category fibred in groupoids over
$\mathfrak{X}$
consisting of the same objects and all cartesian morphisms is a category fibred in groupoids over
![]() $\mathscr{S}$
. We denote it by
$\mathscr{S}$
. We denote it by
![]() $\mathfrak{X}_{\text{cfg}}$
and call it the underlying category fibred in groupoids.
$\mathfrak{X}_{\text{cfg}}$
and call it the underlying category fibred in groupoids.
Definition 1.8. A category
![]() $\mathfrak{X}$
over
$\mathfrak{X}$
over
![]() $\mathscr{S}$
is an
$\mathscr{S}$
is an
![]() $\mathscr{O}$
-linear category over
$\mathscr{O}$
-linear category over
![]() $\mathscr{S}$
if for every
$\mathscr{S}$
if for every
![]() $f:S^{\prime }\rightarrow S$
in
$f:S^{\prime }\rightarrow S$
in
![]() $\mathscr{S}$
and all
$\mathscr{S}$
and all
![]() $x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
$x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
![]() $x\in \mathfrak{X}(S)$
, the set
$x\in \mathfrak{X}(S)$
, the set
![]() $\operatorname{Hom}_{f}(x^{\prime },x)$
is endowed with the structure of an
$\operatorname{Hom}_{f}(x^{\prime },x)$
is endowed with the structure of an
![]() $\mathscr{O}(S^{\prime })$
-module in such a way that for every pair of morphisms
$\mathscr{O}(S^{\prime })$
-module in such a way that for every pair of morphisms
![]() $g:S^{\prime \prime }\rightarrow S^{\prime }$
,
$g:S^{\prime \prime }\rightarrow S^{\prime }$
,
![]() $f:S^{\prime }\rightarrow S$
and every triple of objects
$f:S^{\prime }\rightarrow S$
and every triple of objects
![]() $x^{\prime \prime }\in \mathfrak{X}(S^{\prime \prime })$
,
$x^{\prime \prime }\in \mathfrak{X}(S^{\prime \prime })$
,
![]() $x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
$x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
![]() $x\in \mathfrak{X}(S)$
, the composition
$x\in \mathfrak{X}(S)$
, the composition
is
![]() $\mathscr{O}(S^{\prime })$
-bilinear.
$\mathscr{O}(S^{\prime })$
-bilinear.
An
![]() $\mathscr{O}$
-linear functor
$\mathscr{O}$
-linear functor
![]() $F:\mathfrak{X}\rightarrow \mathfrak{Y}$
between
$F:\mathfrak{X}\rightarrow \mathfrak{Y}$
between
![]() $\mathscr{O}$
-linear categories is a functor of categories over
$\mathscr{O}$
-linear categories is a functor of categories over
![]() $\mathscr{S}$
such that for every
$\mathscr{S}$
such that for every
![]() $f:S^{\prime }\rightarrow S$
and all
$f:S^{\prime }\rightarrow S$
and all
![]() $x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
$x^{\prime }\in \mathfrak{X}(S^{\prime })$
,
![]() $x\in \mathfrak{X}(S)$
, the map
$x\in \mathfrak{X}(S)$
, the map
![]() $\operatorname{Hom}_{f}(x^{\prime },x)\rightarrow \operatorname{Hom}_{f}(F(x^{\prime }),F(x))$
is
$\operatorname{Hom}_{f}(x^{\prime },x)\rightarrow \operatorname{Hom}_{f}(F(x^{\prime }),F(x))$
is
![]() $\mathscr{O}(S^{\prime })$
-linear.
$\mathscr{O}(S^{\prime })$
-linear.
Assume given an
![]() $\mathscr{O}$
-linear fibred category
$\mathscr{O}$
-linear fibred category
![]() $\mathfrak{X}$
over
$\mathfrak{X}$
over
![]() $\mathscr{S}$
. Pullback in
$\mathscr{S}$
. Pullback in
![]() $\mathfrak{X}$
is
$\mathfrak{X}$
is
![]() $\mathscr{O}$
-linear, i.e., if
$\mathscr{O}$
-linear, i.e., if
![]() $f:S^{\prime }\rightarrow S$
is a morphism in
$f:S^{\prime }\rightarrow S$
is a morphism in
![]() $\mathscr{S}$
and
$\mathscr{S}$
and
![]() $x,y\in \mathfrak{X}(S)$
are objects with pullbacks
$x,y\in \mathfrak{X}(S)$
are objects with pullbacks
![]() $x^{\prime },y^{\prime }\in \mathfrak{X}(S^{\prime })$
, the pullback map
$x^{\prime },y^{\prime }\in \mathfrak{X}(S^{\prime })$
, the pullback map
![]() $f^{\ast }:\operatorname{Hom}_{S}(x,y)\rightarrow \operatorname{Hom}_{S^{\prime }}(x^{\prime },y^{\prime })$
is
$f^{\ast }:\operatorname{Hom}_{S}(x,y)\rightarrow \operatorname{Hom}_{S^{\prime }}(x^{\prime },y^{\prime })$
is
![]() $\mathscr{O}(S)$
-linear.
$\mathscr{O}(S)$
-linear.
So, if we fix objects
![]() $x,y\in \mathfrak{X}(S)$
, the presheaf
$x,y\in \mathfrak{X}(S)$
, the presheaf
![]() $\operatorname{Hom̲}_{S}(x,y)$
over the usual small étale site of
$\operatorname{Hom̲}_{S}(x,y)$
over the usual small étale site of
![]() $S$
, defined by
$S$
, defined by
![]() $\operatorname{Hom̲}_{S}(x,y)(T)=\operatorname{Hom}_{T}(x|_{T},y|_{T})$
for every étale
$\operatorname{Hom̲}_{S}(x,y)(T)=\operatorname{Hom}_{T}(x|_{T},y|_{T})$
for every étale
![]() $T\rightarrow S$
, is a presheaf of
$T\rightarrow S$
, is a presheaf of
![]() $\mathscr{O}_{S_{\acute{\text{e}}\text{t}}}$
-modules. Moreover, for any morphism
$\mathscr{O}_{S_{\acute{\text{e}}\text{t}}}$
-modules. Moreover, for any morphism
![]() $f:S^{\prime }\rightarrow S$
in
$f:S^{\prime }\rightarrow S$
in
![]() $\mathscr{S}$
, we have a natural homomorphism of presheaves of
$\mathscr{S}$
, we have a natural homomorphism of presheaves of
![]() $\mathscr{O}_{S}$
-modules
$\mathscr{O}_{S}$
-modules
![]() $\operatorname{Hom̲}_{S}(x,y)\rightarrow f_{\ast }\operatorname{Hom̲}_{S^{\prime }}(x^{\prime },y^{\prime })$
. Put together, the small presheaves
$\operatorname{Hom̲}_{S}(x,y)\rightarrow f_{\ast }\operatorname{Hom̲}_{S^{\prime }}(x^{\prime },y^{\prime })$
. Put together, the small presheaves
![]() $\operatorname{Hom̲}_{T}(x,y)$
, as
$\operatorname{Hom̲}_{T}(x,y)$
, as
![]() $T\rightarrow S$
varies over the big étale site of the scheme
$T\rightarrow S$
varies over the big étale site of the scheme
![]() $S$
, form a big presheaf, which we denote by
$S$
, form a big presheaf, which we denote by
![]() $\operatorname{Hom̲}(x,y)$
.
$\operatorname{Hom̲}(x,y)$
.
Definition 1.9. A linear algebraic stack is an
![]() $\mathscr{O}$
-linear fibred category
$\mathscr{O}$
-linear fibred category
![]() $\mathfrak{X}$
over
$\mathfrak{X}$
over
![]() $\mathscr{S}$
, such that:
$\mathscr{S}$
, such that:
(i) for every object
 $S\in \mathscr{S}$
and every pair
$S\in \mathscr{S}$
and every pair
 $x,y\in \mathfrak{X}(S)$
, the presheaf
$x,y\in \mathfrak{X}(S)$
, the presheaf
 $\operatorname{Hom̲}(x,y)$
on the big étale site of the scheme
$\operatorname{Hom̲}(x,y)$
on the big étale site of the scheme
 $S$
is a locally coherent representable sheaf of
$S$
is a locally coherent representable sheaf of
 $\mathscr{O}_{S}$
-modules;
$\mathscr{O}_{S}$
-modules;(ii) the underlying category fibred in groupoids
 $\mathfrak{X}_{\text{cfg}}\rightarrow \mathscr{S}$
is an algebraic stack over
$\mathfrak{X}_{\text{cfg}}\rightarrow \mathscr{S}$
is an algebraic stack over
 $R$
(locally of finite type).
$R$
(locally of finite type).
A morphism of linear algebraic stacks is an
![]() $\mathscr{O}$
-linear cartesian functor over
$\mathscr{O}$
-linear cartesian functor over
![]() $\mathscr{S}$
.
$\mathscr{S}$
.
Remark 1.10. If
![]() $\mathfrak{X}$
is a linear algebraic stack with underling algebraic stack
$\mathfrak{X}$
is a linear algebraic stack with underling algebraic stack
![]() $X=\mathfrak{X}_{\text{cfg}}$
, there exists a locally coherent representable sheaf
$X=\mathfrak{X}_{\text{cfg}}$
, there exists a locally coherent representable sheaf
![]() $\mathscr{H}$
over
$\mathscr{H}$
over
![]() $X\times X$
that represents the sheaf over
$X\times X$
that represents the sheaf over
![]() $X\times X$
whose set of sections over the pair
$X\times X$
whose set of sections over the pair
![]() $x,y\in X(S)$
is the
$x,y\in X(S)$
is the
![]() $\mathscr{O}(S)$
-module
$\mathscr{O}(S)$
-module
![]() $\operatorname{Hom}_{S}(x,y)$
. The sheaf
$\operatorname{Hom}_{S}(x,y)$
. The sheaf
![]() $\mathscr{H}$
is the universal sheaf of homomorphisms. The subsheaf
$\mathscr{H}$
is the universal sheaf of homomorphisms. The subsheaf
![]() $\mathscr{I}\subset \mathscr{H}$
representing isomorphisms is naturally identified with
$\mathscr{I}\subset \mathscr{H}$
representing isomorphisms is naturally identified with
![]() $X$
and the projection to
$X$
and the projection to
![]() $X\times X$
with the diagonal.
$X\times X$
with the diagonal.
Pulling back
![]() $\mathscr{H}$
via the diagonal to
$\mathscr{H}$
via the diagonal to
![]() $X$
, we obtain the universal sheaf of endomorphisms
$X$
, we obtain the universal sheaf of endomorphisms
![]() $\mathscr{E}\rightarrow X$
, which represents the sheaf whose set of sections over
$\mathscr{E}\rightarrow X$
, which represents the sheaf whose set of sections over
![]() $x\in X(S)$
is the
$x\in X(S)$
is the
![]() $\mathscr{O}(S)$
-algebra
$\mathscr{O}(S)$
-algebra
![]() $\operatorname{End}_{S}(x)$
. Let us emphasize that
$\operatorname{End}_{S}(x)$
. Let us emphasize that
![]() $\mathscr{E}\rightarrow X$
is a representable morphism of algebraic stacks, which is at the same time a sheaf of algebras and a locally coherent representable sheaf of
$\mathscr{E}\rightarrow X$
is a representable morphism of algebraic stacks, which is at the same time a sheaf of algebras and a locally coherent representable sheaf of
![]() $\mathscr{O}_{X}$
-modules.
$\mathscr{O}_{X}$
-modules.
The linear algebraic stack
![]() $\mathfrak{X}$
can be reconstructed from its underlying algebraic stack
$\mathfrak{X}$
can be reconstructed from its underlying algebraic stack
![]() $X$
and the representable sheaf of
$X$
and the representable sheaf of
![]() $\mathscr{O}_{X\times X}$
-algebras
$\mathscr{O}_{X\times X}$
-algebras
![]() $\mathscr{H}$
. We leave it to the reader to write down axioms for the pair
$\mathscr{H}$
. We leave it to the reader to write down axioms for the pair
![]() $(X,\mathscr{H})$
that ensure that
$(X,\mathscr{H})$
that ensure that
![]() $(X,\mathscr{H})$
comes from a linear algebraic stack.
$(X,\mathscr{H})$
comes from a linear algebraic stack.
Examples
Example 1.11. Let
![]() $X$
be a projective
$X$
be a projective
![]() $R$
-scheme. The linear stack
$R$
-scheme. The linear stack
![]() $\mathfrak{Coh}_{X}$
has as objects lying over the
$\mathfrak{Coh}_{X}$
has as objects lying over the
![]() $R$
-scheme
$R$
-scheme
![]() $S$
the coherent sheaves on
$S$
the coherent sheaves on
![]() $X\times S$
, which are flat over
$X\times S$
, which are flat over
![]() $S$
. For a morphism of
$S$
. For a morphism of
![]() $R$
-schemes
$R$
-schemes
![]() $f:S^{\prime }\rightarrow S$
, and
$f:S^{\prime }\rightarrow S$
, and
![]() $\mathscr{F}^{\prime }\in \mathfrak{Coh}_{X}(S^{\prime })$
and
$\mathscr{F}^{\prime }\in \mathfrak{Coh}_{X}(S^{\prime })$
and
![]() $\mathscr{F}\in \mathfrak{Coh}_{X}(S)$
, we set
$\mathscr{F}\in \mathfrak{Coh}_{X}(S)$
, we set
![]() $\operatorname{Hom}_{f}(\mathscr{F}^{\prime },\mathscr{F})=\operatorname{Hom}_{\mathscr{O}_{X\times S^{\prime }}}(\mathscr{F}^{\prime },f^{\ast }\mathscr{F})$
. A morphism
$\operatorname{Hom}_{f}(\mathscr{F}^{\prime },\mathscr{F})=\operatorname{Hom}_{\mathscr{O}_{X\times S^{\prime }}}(\mathscr{F}^{\prime },f^{\ast }\mathscr{F})$
. A morphism
![]() $\mathscr{F}^{\prime }\rightarrow \mathscr{F}$
in
$\mathscr{F}^{\prime }\rightarrow \mathscr{F}$
in
![]() $\mathfrak{Coh}_{X}$
over
$\mathfrak{Coh}_{X}$
over
![]() $f$
in
$f$
in
![]() $\mathscr{S}$
is cartesian if it induces an isomorphism
$\mathscr{S}$
is cartesian if it induces an isomorphism
![]() $\mathscr{F}^{\prime }\cong f^{\ast }\mathscr{F}$
.
$\mathscr{F}^{\prime }\cong f^{\ast }\mathscr{F}$
.
The linear stack
![]() $\mathfrak{Coh}_{X}$
is algebraic.
$\mathfrak{Coh}_{X}$
is algebraic.
To see this, suppose
![]() $\mathscr{F}$
and
$\mathscr{F}$
and
![]() $\mathscr{G}$
are coherent sheaves on
$\mathscr{G}$
are coherent sheaves on
![]() $X\times S$
, flat over
$X\times S$
, flat over
![]() $S$
. The fact that
$S$
. The fact that
![]() $\operatorname{Hom̲}(\mathscr{F},\mathscr{G})$
is a locally coherent representable sheaf of
$\operatorname{Hom̲}(\mathscr{F},\mathscr{G})$
is a locally coherent representable sheaf of
![]() $\mathscr{O}_{X}$
-modules follows from the fact that there exists a coherent sheaf
$\mathscr{O}_{X}$
-modules follows from the fact that there exists a coherent sheaf
![]() $\mathscr{N}$
on the big étale site of
$\mathscr{N}$
on the big étale site of
![]() $S$
such that
$S$
such that
![]() $\operatorname{Hom̲}(\mathscr{F},\mathscr{G})=\mathscr{N}^{\vee }$
(see [Reference Grothendieck and DieudonnéGD67, EGA III 7.7.8, 7.7.9]). In fact, for a morphism of schemes
$\operatorname{Hom̲}(\mathscr{F},\mathscr{G})=\mathscr{N}^{\vee }$
(see [Reference Grothendieck and DieudonnéGD67, EGA III 7.7.8, 7.7.9]). In fact, for a morphism of schemes
![]() $T\rightarrow S$
, we have
$T\rightarrow S$
, we have
![]() $\operatorname{Hom̲}_{T}(\mathscr{F},\mathscr{G})={\unicode[STIX]{x1D70B}_{T}}_{\ast }\mathscr{H}om(\mathscr{F}_{X\times T},\mathscr{G}_{X\times T})$
. The fact that pushforward does not commute with arbitrary pullbacks means that
$\operatorname{Hom̲}_{T}(\mathscr{F},\mathscr{G})={\unicode[STIX]{x1D70B}_{T}}_{\ast }\mathscr{H}om(\mathscr{F}_{X\times T},\mathscr{G}_{X\times T})$
. The fact that pushforward does not commute with arbitrary pullbacks means that
![]() $\operatorname{Hom̲}(\mathscr{F},\mathscr{G})$
is not in general cartesian and hence not in general coherent. On the other hand, by [Reference Grothendieck and DieudonnéGD67, EGA III 7.7.8, 7.7.9], we have
$\operatorname{Hom̲}(\mathscr{F},\mathscr{G})$
is not in general cartesian and hence not in general coherent. On the other hand, by [Reference Grothendieck and DieudonnéGD67, EGA III 7.7.8, 7.7.9], we have
![]() ${\unicode[STIX]{x1D70B}_{T}}_{\ast }\mathscr{H}om(\mathscr{F}_{X\times T},\mathscr{G}_{X\times T})=(\mathscr{N}_{T})^{\vee }$
, which proves that, indeed,
${\unicode[STIX]{x1D70B}_{T}}_{\ast }\mathscr{H}om(\mathscr{F}_{X\times T},\mathscr{G}_{X\times T})=(\mathscr{N}_{T})^{\vee }$
, which proves that, indeed,
![]() $\operatorname{Hom̲}(\mathscr{F},\mathscr{G})=\mathscr{N}^{\vee }$
.
$\operatorname{Hom̲}(\mathscr{F},\mathscr{G})=\mathscr{N}^{\vee }$
.
The fact that
![]() $(\mathfrak{Coh}_{X})_{\text{cfg}}$
is algebraic and locally of finite type is proved in [Reference Laumon and Moret-BaillyLMB00, 4.6.2.1].
$(\mathfrak{Coh}_{X})_{\text{cfg}}$
is algebraic and locally of finite type is proved in [Reference Laumon and Moret-BaillyLMB00, 4.6.2.1].
Example 1.12. As a special case of the previous example, consider the case
![]() $X=\operatorname{Spec}R$
. Then the linear algebraic stack
$X=\operatorname{Spec}R$
. Then the linear algebraic stack
![]() $\mathfrak{Coh}_{\operatorname{Spec}R}$
is the linear stack of vector bundles, denoted by
$\mathfrak{Coh}_{\operatorname{Spec}R}$
is the linear stack of vector bundles, denoted by
![]() $\mathfrak{Vect}$
. The underlying algebraic stack
$\mathfrak{Vect}$
. The underlying algebraic stack
![]() $\mathfrak{Vect}_{\text{cfg}}$
is the disjoint union
$\mathfrak{Vect}_{\text{cfg}}$
is the disjoint union
![]() $\coprod _{n\geqslant 0}B\operatorname{GL}_{n}$
. The sheaf
$\coprod _{n\geqslant 0}B\operatorname{GL}_{n}$
. The sheaf
![]() $\mathscr{H}$
over
$\mathscr{H}$
over
is given by the natural representation
![]() $M(m\times n)$
of
$M(m\times n)$
of
![]() $\operatorname{GL}_{n}\times \operatorname{GL}_{m}$
over
$\operatorname{GL}_{n}\times \operatorname{GL}_{m}$
over
![]() $B(\operatorname{GL}_{n}\times \operatorname{GL}_{m})$
.
$B(\operatorname{GL}_{n}\times \operatorname{GL}_{m})$
.
Example 1.13. A generalization of
![]() $\mathfrak{Vect}$
in a different direction is given by quiver representations.
$\mathfrak{Vect}$
in a different direction is given by quiver representations.
Let
![]() $Q$
be a quiver. The stack of representations of
$Q$
be a quiver. The stack of representations of
![]() $Q$
, denoted by
$Q$
, denoted by
![]() $\mathfrak{Rep}_{Q}$
, has as
$\mathfrak{Rep}_{Q}$
, has as
![]() $\mathfrak{Rep}_{Q}(S)$
the set of diagrams
$\mathfrak{Rep}_{Q}(S)$
the set of diagrams
![]() $(\mathscr{F})$
in the shape of
$(\mathscr{F})$
in the shape of
![]() $Q$
of locally free finite rank
$Q$
of locally free finite rank
![]() $\mathscr{O}_{S}$
-modules. For a morphism
$\mathscr{O}_{S}$
-modules. For a morphism
![]() $f:S^{\prime }\rightarrow S$
of
$f:S^{\prime }\rightarrow S$
of
![]() $R$
-schemes, we have that
$R$
-schemes, we have that
![]() $\operatorname{Hom}_{f}(\mathscr{F}^{\prime },\mathscr{F})$
is the
$\operatorname{Hom}_{f}(\mathscr{F}^{\prime },\mathscr{F})$
is the
![]() $\mathscr{O}(S^{\prime })$
-module of homomorphisms
$\mathscr{O}(S^{\prime })$
-module of homomorphisms
![]() $\mathscr{F}^{\prime }\rightarrow f^{\ast }\mathscr{F}$
of diagrams of locally free
$\mathscr{F}^{\prime }\rightarrow f^{\ast }\mathscr{F}$
of diagrams of locally free
![]() $\mathscr{O}_{S^{\prime }}$
-modules.
$\mathscr{O}_{S^{\prime }}$
-modules.
Example 1.14. As a toy example, let
![]() $A$
be a vector bundle over
$A$
be a vector bundle over
![]() $\operatorname{Spec}R$
, endowed with the structure of a sheaf of
$\operatorname{Spec}R$
, endowed with the structure of a sheaf of
![]() $\mathscr{O}_{\operatorname{Spec}R}$
-modules, with smooth group scheme of units
$\mathscr{O}_{\operatorname{Spec}R}$
-modules, with smooth group scheme of units
![]() $A^{\times }$
, also of finite type. Then we define the linear stack of
$A^{\times }$
, also of finite type. Then we define the linear stack of
![]() $A^{\times }$
-torsors to have as objects over the
$A^{\times }$
-torsors to have as objects over the
![]() $R$
-scheme
$R$
-scheme
![]() $S$
the right
$S$
the right
![]() $A^{\times }$
-torsors over
$A^{\times }$
-torsors over
![]() $S$
, and for
$S$
, and for
![]() $f:S^{\prime }\rightarrow S$
and
$f:S^{\prime }\rightarrow S$
and
![]() $A^{\times }$
-torsors
$A^{\times }$
-torsors
![]() $P^{\prime }$
over
$P^{\prime }$
over
![]() $S^{\prime }$
and
$S^{\prime }$
and
![]() $P$
over
$P$
over
![]() $S$
, we set
$S$
, we set
![]() $\operatorname{Hom}_{f}(P^{\prime },P)=\operatorname{Hom}_{S^{\prime }}(P^{\prime },f^{\ast }P)=P^{\prime }\times _{A^{\times }}A\times _{A^{\times }}f^{\ast }P$
. In this example, the underlying algebraic stack is
$\operatorname{Hom}_{f}(P^{\prime },P)=\operatorname{Hom}_{S^{\prime }}(P^{\prime },f^{\ast }P)=P^{\prime }\times _{A^{\times }}A\times _{A^{\times }}f^{\ast }P$
. In this example, the underlying algebraic stack is
![]() $BA^{\times }$
and we have
$BA^{\times }$
and we have
![]() $\mathscr{H}=A^{\times }\backslash A/A^{\times }$
.
$\mathscr{H}=A^{\times }\backslash A/A^{\times }$
.
The case
![]() $A=0$
is not excluded. The associated linear stack is
$A=0$
is not excluded. The associated linear stack is
![]() $\operatorname{id}:\mathscr{S}\rightarrow \mathscr{S}$
. All
$\operatorname{id}:\mathscr{S}\rightarrow \mathscr{S}$
. All
![]() $\operatorname{Hom}_{f}(x,y)$
are singletons, endowed with their unique module structure. This stack is represented by
$\operatorname{Hom}_{f}(x,y)$
are singletons, endowed with their unique module structure. This stack is represented by
![]() $\operatorname{Spec}R$
. It can also be thought of as the stack of zero-dimensional vector bundles.
$\operatorname{Spec}R$
. It can also be thought of as the stack of zero-dimensional vector bundles.
Substacks
Let
![]() $\mathfrak{X}$
be a linear algebraic stack with underlying algebraic stack
$\mathfrak{X}$
be a linear algebraic stack with underlying algebraic stack
![]() $X=\mathfrak{X}_{\text{cfg}}$
. If
$X=\mathfrak{X}_{\text{cfg}}$
. If
![]() $Y\subset X$
is a locally closed algebraic substack, there is a canonical linear algebraic stack
$Y\subset X$
is a locally closed algebraic substack, there is a canonical linear algebraic stack
![]() $\mathfrak{Y}$
with underlying algebraic stack
$\mathfrak{Y}$
with underlying algebraic stack
![]() $\mathfrak{Y}_{\text{cfg}}=Y$
. In fact, we can define
$\mathfrak{Y}_{\text{cfg}}=Y$
. In fact, we can define
![]() $\mathfrak{Y}$
to be the full subcategory of
$\mathfrak{Y}$
to be the full subcategory of
![]() $\mathfrak{X}$
consisting of objects which are in
$\mathfrak{X}$
consisting of objects which are in
![]() $Y$
.
$Y$
.
In this situation, we call
![]() $\mathfrak{Y}\rightarrow \mathfrak{X}$
a locally closed linear substack of
$\mathfrak{Y}\rightarrow \mathfrak{X}$
a locally closed linear substack of
![]() $\mathfrak{X}$
.
$\mathfrak{X}$
.
Fibred products
Let
![]() $F:\mathfrak{X}\rightarrow \mathfrak{Z}$
and
$F:\mathfrak{X}\rightarrow \mathfrak{Z}$
and
![]() $G:\mathfrak{Y}\rightarrow \mathfrak{Z}$
be cartesian morphisms of
$G:\mathfrak{Y}\rightarrow \mathfrak{Z}$
be cartesian morphisms of
![]() $\mathscr{O}$
-linear fibred categories. We define a new
$\mathscr{O}$
-linear fibred categories. We define a new
![]() $\mathscr{O}$
-linear fibred category
$\mathscr{O}$
-linear fibred category
![]() $\mathfrak{W}$
as follows: objects of
$\mathfrak{W}$
as follows: objects of
![]() $\mathfrak{W}$
over the object
$\mathfrak{W}$
over the object
![]() $T$
of
$T$
of
![]() $\mathscr{S}$
are triples
$\mathscr{S}$
are triples
![]() $(x,\unicode[STIX]{x1D6FC},y)$
, where
$(x,\unicode[STIX]{x1D6FC},y)$
, where
![]() $x$
is an
$x$
is an
![]() $\mathfrak{X}$
-object over
$\mathfrak{X}$
-object over
![]() $T$
,
$T$
,
![]() $y$
is a
$y$
is a
![]() $\mathfrak{Y}$
-object over
$\mathfrak{Y}$
-object over
![]() $T$
, and
$T$
, and
![]() $\unicode[STIX]{x1D6FC}$
is an isomorphism
$\unicode[STIX]{x1D6FC}$
is an isomorphism
![]() $\unicode[STIX]{x1D6FC}:F(x)\rightarrow G(y)$
over
$\unicode[STIX]{x1D6FC}:F(x)\rightarrow G(y)$
over
![]() $T$
. A morphism from
$T$
. A morphism from
![]() $(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
to
$(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
to
![]() $(x,\unicode[STIX]{x1D6FC},y)$
over
$(x,\unicode[STIX]{x1D6FC},y)$
over
![]() $T^{\prime }\rightarrow T$
is a pair of morphisms
$T^{\prime }\rightarrow T$
is a pair of morphisms
![]() $f:x^{\prime }\rightarrow x$
over
$f:x^{\prime }\rightarrow x$
over
![]() $T^{\prime }\rightarrow T$
and
$T^{\prime }\rightarrow T$
and
![]() $g:y^{\prime }\rightarrow y$
over
$g:y^{\prime }\rightarrow y$
over
![]() $T^{\prime }\rightarrow T$
such that
$T^{\prime }\rightarrow T$
such that
![]() $\unicode[STIX]{x1D6FC}\circ F(f)=G(g)\circ \unicode[STIX]{x1D6FC}^{\prime }$
.
$\unicode[STIX]{x1D6FC}\circ F(f)=G(g)\circ \unicode[STIX]{x1D6FC}^{\prime }$
.
In other words, we can write the set of morphisms from
![]() $(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
to
$(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
to
![]() $(x,\unicode[STIX]{x1D6FC},y)$
over
$(x,\unicode[STIX]{x1D6FC},y)$
over
![]() $\unicode[STIX]{x1D711}:T^{\prime }\rightarrow T$
as the fibred product
$\unicode[STIX]{x1D711}:T^{\prime }\rightarrow T$
as the fibred product
and as each of the sets in this fibred product is an
![]() $\mathscr{O}(T^{\prime })$
-module, and the maps are linear, this fibred product is also an
$\mathscr{O}(T^{\prime })$
-module, and the maps are linear, this fibred product is also an
![]() $\mathscr{O}(T^{\prime })$
-module. We leave it to the reader to verify that composition is bilinear.
$\mathscr{O}(T^{\prime })$
-module. We leave it to the reader to verify that composition is bilinear.
Let us verify that
![]() $\mathfrak{W}$
is a fibred category. Suppose that
$\mathfrak{W}$
is a fibred category. Suppose that
![]() $(x,\unicode[STIX]{x1D6FC},y)$
is a triple over
$(x,\unicode[STIX]{x1D6FC},y)$
is a triple over
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D711}:T^{\prime }\rightarrow T$
a morphism in
$\unicode[STIX]{x1D711}:T^{\prime }\rightarrow T$
a morphism in
![]() $\mathscr{S}$
. We construct a triple
$\mathscr{S}$
. We construct a triple
![]() $(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
over
$(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
over
![]() $T^{\prime }$
by taking as
$T^{\prime }$
by taking as
![]() $x^{\prime }$
a pullback of
$x^{\prime }$
a pullback of
![]() $x$
via
$x$
via
![]() $\unicode[STIX]{x1D711}$
and as
$\unicode[STIX]{x1D711}$
and as
![]() $y^{\prime }$
a pullback of
$y^{\prime }$
a pullback of
![]() $y$
via
$y$
via
![]() $\unicode[STIX]{x1D711}$
. Then, as
$\unicode[STIX]{x1D711}$
. Then, as
![]() $G$
is cartesian,
$G$
is cartesian,
![]() $G(y^{\prime })$
is a pullback of
$G(y^{\prime })$
is a pullback of
![]() $G(y)$
via
$G(y)$
via
![]() $\unicode[STIX]{x1D711}$
. Hence, there exists a unique morphism
$\unicode[STIX]{x1D711}$
. Hence, there exists a unique morphism
![]() $\unicode[STIX]{x1D6FC}^{\prime }:F(x^{\prime })\rightarrow G(y^{\prime })$
covering
$\unicode[STIX]{x1D6FC}^{\prime }:F(x^{\prime })\rightarrow G(y^{\prime })$
covering
![]() $T^{\prime }$
such that
$T^{\prime }$
such that
![]() $\unicode[STIX]{x1D6FC}\circ F(x^{\prime }\rightarrow x)=G(y^{\prime }\rightarrow y)\circ \unicode[STIX]{x1D6FC}^{\prime }$
. Then
$\unicode[STIX]{x1D6FC}\circ F(x^{\prime }\rightarrow x)=G(y^{\prime }\rightarrow y)\circ \unicode[STIX]{x1D6FC}^{\prime }$
. Then
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is cartesian, because cartesian morphisms satisfy the necessary ‘two out of three’ property. Then
$\unicode[STIX]{x1D6FC}^{\prime }$
is cartesian, because cartesian morphisms satisfy the necessary ‘two out of three’ property. Then
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is invertible, because cartesian morphisms covering an identity are invertible. The triple
$\unicode[STIX]{x1D6FC}^{\prime }$
is invertible, because cartesian morphisms covering an identity are invertible. The triple
![]() $(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
comes with a given morphism to
$(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
comes with a given morphism to
![]() $(x,\unicode[STIX]{x1D6FC},y)$
that covers
$(x,\unicode[STIX]{x1D6FC},y)$
that covers
![]() $\unicode[STIX]{x1D711}$
. It is easily verified that this morphism is cartesian.
$\unicode[STIX]{x1D711}$
. It is easily verified that this morphism is cartesian.
Therefore,
![]() $\mathfrak{W}$
is an
$\mathfrak{W}$
is an
![]() $\mathscr{O}$
-linear fibred category. By construction, the two projections
$\mathscr{O}$
-linear fibred category. By construction, the two projections
![]() $\mathfrak{W}\rightarrow \mathfrak{X}$
and
$\mathfrak{W}\rightarrow \mathfrak{X}$
and
![]() $\mathfrak{W}\rightarrow \mathfrak{Y}$
are cartesian. We call
$\mathfrak{W}\rightarrow \mathfrak{Y}$
are cartesian. We call
![]() $\mathfrak{W}$
the fibred product of
$\mathfrak{W}$
the fibred product of
![]() $\mathfrak{X}$
and
$\mathfrak{X}$
and
![]() $\mathfrak{Y}$
over
$\mathfrak{Y}$
over
![]() $\mathfrak{Z}$
.
$\mathfrak{Z}$
.
Suppose
![]() $\mathfrak{X}$
,
$\mathfrak{X}$
,
![]() $\mathfrak{Y}$
, and
$\mathfrak{Y}$
, and
![]() $\mathfrak{Z}$
are algebraic, with underlying algebraic stacks
$\mathfrak{Z}$
are algebraic, with underlying algebraic stacks
![]() $X$
,
$X$
,
![]() $Y$
, and
$Y$
, and
![]() $Z$
, respectively. For triples
$Z$
, respectively. For triples
![]() $(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
and
$(x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime })$
and
![]() $(x,\unicode[STIX]{x1D6FC},y)$
over
$(x,\unicode[STIX]{x1D6FC},y)$
over
![]() $S$
, the presheaf
$S$
, the presheaf
![]() $\operatorname{Hom̲}((x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime }),(x,\unicode[STIX]{x1D6FC},y))$
is equal to the fibred product
$\operatorname{Hom̲}((x^{\prime },\unicode[STIX]{x1D6FC}^{\prime },y^{\prime }),(x,\unicode[STIX]{x1D6FC},y))$
is equal to the fibred product
and is therefore a locally coherent representable sheaf of
![]() $\mathscr{O}_{S}$
-modules. We see that
$\mathscr{O}_{S}$
-modules. We see that
![]() $\mathfrak{W}$
is again a linear algebraic stack. Moreover, the underlying algebraic stack of
$\mathfrak{W}$
is again a linear algebraic stack. Moreover, the underlying algebraic stack of
![]() $W$
is the fibred product
$W$
is the fibred product
![]() $X\times _{Z}Y$
.
$X\times _{Z}Y$
.
Lack of locality
Remark 1.15. Suppose
![]() $\mathfrak{X}$
and
$\mathfrak{X}$
and
![]() $\mathfrak{Y}$
are linear algebraic stacks with underlying algebraic stacks
$\mathfrak{Y}$
are linear algebraic stacks with underlying algebraic stacks
![]() $X$
and
$X$
and
![]() $Y$
. We can construct a disjoint union linear algebraic stack
$Y$
. We can construct a disjoint union linear algebraic stack
![]() $\mathfrak{X}\amalg \mathfrak{Y}$
whose underlying algebraic stack is
$\mathfrak{X}\amalg \mathfrak{Y}$
whose underlying algebraic stack is
![]() $X\amalg Y$
by declaring all homomorphisms between objects of
$X\amalg Y$
by declaring all homomorphisms between objects of
![]() $\mathfrak{X}$
and objects of
$\mathfrak{X}$
and objects of
![]() $\mathfrak{Y}$
to be zero. This concept of disjoint union is not useful for our purposes. For the linear algebraic stacks we are interested in, the underlying algebraic stack often decomposes into a disjoint union, even though the linear algebraic stack does not. An example is given by the linear stack of vector bundles
$\mathfrak{Y}$
to be zero. This concept of disjoint union is not useful for our purposes. For the linear algebraic stacks we are interested in, the underlying algebraic stack often decomposes into a disjoint union, even though the linear algebraic stack does not. An example is given by the linear stack of vector bundles
![]() $\mathfrak{Vect}$
, Example 1.12.
$\mathfrak{Vect}$
, Example 1.12.
Thus, linear algebraic stacks exhibit less local behaviour than algebraic stacks and are therefore less geometrical. This is one of the reasons we prefer to work with algebroids, rather than linear algebraic stacks.
Special linear stacks
For a linear algebraic stack
![]() $\mathfrak{M}$
, every fibre category
$\mathfrak{M}$
, every fibre category
![]() $\mathfrak{M}(S)$
is an
$\mathfrak{M}(S)$
is an
![]() $R$
-linear category. By putting special requirements on these linear categories, we get stronger notions of linear algebraic stack.
$R$
-linear category. By putting special requirements on these linear categories, we get stronger notions of linear algebraic stack.
For a linear algebraic stack
![]() $\mathfrak{M}$
, we denote the universal sheaf of endomorphisms by
$\mathfrak{M}$
, we denote the universal sheaf of endomorphisms by
![]() $\mathfrak{A}\rightarrow \mathfrak{M}$
.
$\mathfrak{A}\rightarrow \mathfrak{M}$
.
Definition 1.16. A linear algebraic stack
![]() $\mathfrak{M}$
has a zero object if the
$\mathfrak{M}$
has a zero object if the
![]() $R$
-linear category
$R$
-linear category
![]() $\mathfrak{M}(R)$
admits a zero object.
$\mathfrak{M}(R)$
admits a zero object.
If
![]() $\mathfrak{M}$
admits a zero object, then for every
$\mathfrak{M}$
admits a zero object, then for every
![]() $R$
-scheme
$R$
-scheme
![]() $S$
, the
$S$
, the
![]() $R$
-linear category
$R$
-linear category
![]() $\mathfrak{M}(S)$
admits a zero object, namely, the pullback of the zero object in
$\mathfrak{M}(S)$
admits a zero object, namely, the pullback of the zero object in
![]() $\mathfrak{M}(\operatorname{Spec}R)$
via the unique morphism
$\mathfrak{M}(\operatorname{Spec}R)$
via the unique morphism
![]() $S\rightarrow \operatorname{Spec}R$
.
$S\rightarrow \operatorname{Spec}R$
.
A zero object for
![]() $\mathfrak{M}$
defines a section
$\mathfrak{M}$
defines a section
![]() $\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
, which is an isomorphism onto the closed substack of
$\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
, which is an isomorphism onto the closed substack of
![]() $\mathfrak{M}$
defined by the condition
$\mathfrak{M}$
defined by the condition
![]() $1=0$
inside
$1=0$
inside
![]() $\mathfrak{A}$
.
$\mathfrak{A}$
.
If
![]() $\mathfrak{M}$
admits a zero object, we denote the complement of the zero object in
$\mathfrak{M}$
admits a zero object, we denote the complement of the zero object in
![]() $\mathfrak{M}$
by
$\mathfrak{M}$
by
![]() $\mathfrak{M}_{\ast }$
. It is a linear open substack of
$\mathfrak{M}_{\ast }$
. It is a linear open substack of
![]() $\mathfrak{M}$
.
$\mathfrak{M}$
.
Definition 1.17. The linear algebraic stack
![]() $\mathfrak{M}$
admits direct sums if for every
$\mathfrak{M}$
admits direct sums if for every
![]() $R$
-scheme
$R$
-scheme
![]() $S$
, the
$S$
, the
![]() $R$
-linear category
$R$
-linear category
![]() $\mathfrak{M}(S)$
admits all (finite) direct sums.
$\mathfrak{M}(S)$
admits all (finite) direct sums.
The pullback functor
![]() $\mathfrak{M}(S)\rightarrow \mathfrak{M}(S^{\prime })$
for a morphism of
$\mathfrak{M}(S)\rightarrow \mathfrak{M}(S^{\prime })$
for a morphism of
![]() $R$
-schemes
$R$
-schemes
![]() $S^{\prime }\rightarrow S$
commutes with direct sums. Hence, if
$S^{\prime }\rightarrow S$
commutes with direct sums. Hence, if
![]() $\mathfrak{M}$
admits direct sums, there is a canonical morphism of linear stacks
$\mathfrak{M}$
admits direct sums, there is a canonical morphism of linear stacks
See also Remark 1.63.
1.3 Finite type algebras
None of our algebras are assumed to be commutative, but they are all assumed to be unital.
Definition 1.18. Let
![]() $X$
be an algebraic stack. By an algebra over
$X$
be an algebraic stack. By an algebra over
![]() $X$
, we mean a sheaf of
$X$
, we mean a sheaf of
![]() $\mathscr{O}_{X}$
-algebras over
$\mathscr{O}_{X}$
-algebras over
![]() $X$
. If the algebra
$X$
. If the algebra
![]() $A$
over the algebraic stack
$A$
over the algebraic stack
![]() $X$
is an algebraic stack itself, i.e., if the structure morphism
$X$
is an algebraic stack itself, i.e., if the structure morphism
![]() $A\rightarrow X$
is a representable morphism of stacks, then we say that
$A\rightarrow X$
is a representable morphism of stacks, then we say that
![]() $A$
is representable. If
$A$
is representable. If
![]() $A$
is represented by a finite type affine stack of the form
$A$
is represented by a finite type affine stack of the form
![]() $\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
for a coherent sheaf
$\operatorname{Spec}_{X}\operatorname{Sym}_{\mathscr{O}_{X}}\mathscr{F}$
for a coherent sheaf
![]() $\mathscr{F}$
over
$\mathscr{F}$
over
![]() $X$
, we call
$X$
, we call
![]() $A$
a finite type algebra over
$A$
a finite type algebra over
![]() $X$
.
$X$
.
For an automorphism
![]() $\unicode[STIX]{x1D711}$
of an algebra
$\unicode[STIX]{x1D711}$
of an algebra
![]() $A$
, we denote the subalgebra of fixed sections by
$A$
, we denote the subalgebra of fixed sections by
![]() $A^{\unicode[STIX]{x1D711}}$
. For a section
$A^{\unicode[STIX]{x1D711}}$
. For a section
![]() $a$
of
$a$
of
![]() $A$
we denote by
$A$
we denote by
![]() $A^{a}$
the subalgebra of sections commuting with
$A^{a}$
the subalgebra of sections commuting with
![]() $a$
.
$a$
.
The sheaf of
![]() $\mathscr{O}_{X}$
-modules underlying a finite type algebra is locally coherent representable.
$\mathscr{O}_{X}$
-modules underlying a finite type algebra is locally coherent representable.
For an automorphism
![]() $\unicode[STIX]{x1D711}$
of a finite type algebra
$\unicode[STIX]{x1D711}$
of a finite type algebra
![]() $A$
, the fixed algebra
$A$
, the fixed algebra
![]() $A^{\unicode[STIX]{x1D711}}$
is again a finite type algebra, because the underlying sheaf of modules is the kernel of
$A^{\unicode[STIX]{x1D711}}$
is again a finite type algebra, because the underlying sheaf of modules is the kernel of
![]() $A\stackrel{1-\unicode[STIX]{x1D711}}{\longrightarrow }A$
.
$A\stackrel{1-\unicode[STIX]{x1D711}}{\longrightarrow }A$
.
If
![]() $\mathfrak{X}$
is a linear algebraic stack with underlying algebraic stack
$\mathfrak{X}$
is a linear algebraic stack with underlying algebraic stack
![]() $X$
, then the universal sheaf of endomorphisms
$X$
, then the universal sheaf of endomorphisms
![]() $\mathscr{E}\rightarrow X$
is a finite type algebra.
$\mathscr{E}\rightarrow X$
is a finite type algebra.
Note that finite type algebras need not have a coherent underlying sheaf of
![]() $\mathscr{O}_{X}$
-modules. For example, let
$\mathscr{O}_{X}$
-modules. For example, let
![]() $X=\mathbb{A}^{1}$
, with coordinate
$X=\mathbb{A}^{1}$
, with coordinate
![]() $t$
, and let
$t$
, and let
![]() $A\rightarrow X$
be the centralizer in
$A\rightarrow X$
be the centralizer in
![]() $(M_{2\times 2})_{X}$
of the matrix
$(M_{2\times 2})_{X}$
of the matrix
![]() $(\begin{smallmatrix}t & 0\\ 0 & 0\end{smallmatrix})$
. In this case, the big sheaf underlying
$(\begin{smallmatrix}t & 0\\ 0 & 0\end{smallmatrix})$
. In this case, the big sheaf underlying
![]() $A$
is not cartesian.
$A$
is not cartesian.
Remark 1.19. Dually, a finite type algebra
![]() $A$
over
$A$
over
![]() $X$
corresponds to a coherent sheaf
$X$
corresponds to a coherent sheaf
![]() $M$
over
$M$
over
![]() $X$
that is endowed with a coalgebra structure
$X$
that is endowed with a coalgebra structure
![]() $(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D700})$
, where
$(\unicode[STIX]{x1D6E5},\unicode[STIX]{x1D700})$
, where
![]() $\unicode[STIX]{x1D6E5}:M\rightarrow M\otimes _{\mathscr{O}_{X}}M$
is an associative comultiplication with counit
$\unicode[STIX]{x1D6E5}:M\rightarrow M\otimes _{\mathscr{O}_{X}}M$
is an associative comultiplication with counit
![]() $\unicode[STIX]{x1D700}:M\rightarrow \mathscr{O}_{X}$
. For any
$\unicode[STIX]{x1D700}:M\rightarrow \mathscr{O}_{X}$
. For any
![]() $X$
-scheme
$X$
-scheme
![]() $U$
, we have
$U$
, we have
![]() $A_{U}=M_{U}^{\vee }$
.
$A_{U}=M_{U}^{\vee }$
.
Inertia representation
Whenever
![]() $A\rightarrow X$
is an algebra over the algebraic stack
$A\rightarrow X$
is an algebra over the algebraic stack
![]() $X$
, we have a tautological morphism of sheaves of groups over
$X$
, we have a tautological morphism of sheaves of groups over
![]() $X$
,
$X$
,
Here,
![]() $I_{X}$
is the inertia stack of
$I_{X}$
is the inertia stack of
![]() $X$
, i.e., the stack of pairs
$X$
, i.e., the stack of pairs
![]() $(x,\unicode[STIX]{x1D711})$
where
$(x,\unicode[STIX]{x1D711})$
where
![]() $x$
is an object of
$x$
is an object of
![]() $X$
and
$X$
and
![]() $\unicode[STIX]{x1D711}$
an automorphism of
$\unicode[STIX]{x1D711}$
an automorphism of
![]() $x$
, and
$x$
, and
![]() $\operatorname{Aut̲}(A)$
is the sheaf of automorphisms of the sheaf of algebras
$\operatorname{Aut̲}(A)$
is the sheaf of automorphisms of the sheaf of algebras
![]() $A$
over
$A$
over
![]() $X$
. To construct (6), consider the stack of sheaves of algebras
$X$
. To construct (6), consider the stack of sheaves of algebras
![]() $\mathfrak{Alg}$
over
$\mathfrak{Alg}$
over
![]() $\mathscr{S}$
, which has as objects over the scheme
$\mathscr{S}$
, which has as objects over the scheme
![]() $S$
the sheaves of
$S$
the sheaves of
![]() $\mathscr{O}_{S}$
-algebras on the usual (small) étale site of
$\mathscr{O}_{S}$
-algebras on the usual (small) étale site of
![]() $S$
. A morphism from the sheaf of
$S$
. A morphism from the sheaf of
![]() $\mathscr{O}_{S^{\prime }}$
-algebras
$\mathscr{O}_{S^{\prime }}$
-algebras
![]() $A^{\prime }$
over
$A^{\prime }$
over
![]() $S^{\prime }$
, covering the morphism of schemes
$S^{\prime }$
, covering the morphism of schemes
![]() $f:S^{\prime }\rightarrow S$
to the sheaf of
$f:S^{\prime }\rightarrow S$
to the sheaf of
![]() $\mathscr{O}_{S}$
-algebras
$\mathscr{O}_{S}$
-algebras
![]() $A$
over
$A$
over
![]() $S$
, is, by definition, an isomorphism of sheaves of
$S$
, is, by definition, an isomorphism of sheaves of
![]() $\mathscr{O}_{S^{\prime }}$
-algebras
$\mathscr{O}_{S^{\prime }}$
-algebras
![]() $A^{\prime }\rightarrow f^{\ast }A$
. The sheaf of algebras
$A^{\prime }\rightarrow f^{\ast }A$
. The sheaf of algebras
![]() $A\rightarrow X$
gives rise to a morphism of
$A\rightarrow X$
gives rise to a morphism of
![]() $\mathscr{S}$
-stacks
$\mathscr{S}$
-stacks
![]() $a:X\rightarrow \mathfrak{Alg}$
. We get an induced morphism on inertia stacks
$a:X\rightarrow \mathfrak{Alg}$
. We get an induced morphism on inertia stacks
![]() $I_{X}\rightarrow I_{\mathfrak{Alg}}$
and notice that
$I_{X}\rightarrow I_{\mathfrak{Alg}}$
and notice that
![]() $a^{\ast }I_{\mathfrak{Alg}}=\operatorname{Aut̲}(A)$
.
$a^{\ast }I_{\mathfrak{Alg}}=\operatorname{Aut̲}(A)$
.
With this definition, an automorphism
![]() $\unicode[STIX]{x1D711}$
of the object
$\unicode[STIX]{x1D711}$
of the object
![]() $x$
of the stack
$x$
of the stack
![]() $X$
is mapped to the inverse of the restriction morphism
$X$
is mapped to the inverse of the restriction morphism
![]() $\unicode[STIX]{x1D711}^{\ast }:A(x)\rightarrow A(x)$
.
$\unicode[STIX]{x1D711}^{\ast }:A(x)\rightarrow A(x)$
.
Lemma 1.20. Suppose
![]() $X$
is a gerbe over the algebraic space
$X$
is a gerbe over the algebraic space
![]() $Y$
and
$Y$
and
![]() $A\rightarrow X$
is an algebra. Then there exists a sheaf of
$A\rightarrow X$
is an algebra. Then there exists a sheaf of
![]() $\mathscr{O}_{Y}$
-algebras
$\mathscr{O}_{Y}$
-algebras
![]() $B$
and an isomorphism
$B$
and an isomorphism
![]() $A\cong B|_{X}$
if and only if the inertia representation
$A\cong B|_{X}$
if and only if the inertia representation
![]() $I_{X}\rightarrow \operatorname{Aut̲}_{X}(A)$
is trivial.
$I_{X}\rightarrow \operatorname{Aut̲}_{X}(A)$
is trivial.
Similarly, if
![]() $X$
is a connected gerbe over the Deligne–Mumford stack
$X$
is a connected gerbe over the Deligne–Mumford stack
![]() $Y$
, then an algebra
$Y$
, then an algebra
![]() $A$
over
$A$
over
![]() $X$
descends to
$X$
descends to
![]() $B$
over
$B$
over
![]() $Y$
if and only if the inertia representation restricts to a trivial homomorphism
$Y$
if and only if the inertia representation restricts to a trivial homomorphism
![]() $I_{X}^{\circ }\rightarrow \operatorname{Aut̲}_{X}(A)$
.
$I_{X}^{\circ }\rightarrow \operatorname{Aut̲}_{X}(A)$
.
In either case,
![]() $A$
is representable or of finite type if and only if
$A$
is representable or of finite type if and only if
![]() $B$
is.
$B$
is.
We can pull back the sheaf of algebras
![]() $A$
over
$A$
over
![]() $X$
, via the structure morphism
$X$
, via the structure morphism
![]() $I_{X}\rightarrow X$
, to obtain the sheaf of algebras
$I_{X}\rightarrow X$
, to obtain the sheaf of algebras
![]() $A|_{I_{X}}$
. This sheaf of algebras is endowed with a tautological automorphism, induced from (6). We shall denote the algebra of invariants for this automorphism by
$A|_{I_{X}}$
. This sheaf of algebras is endowed with a tautological automorphism, induced from (6). We shall denote the algebra of invariants for this automorphism by
![]() $A_{I_{X}}^{\text{fix}}$
.
$A_{I_{X}}^{\text{fix}}$
.
The following statement is somewhat tautological and holds more generally than for algebras.
Proposition 1.21. Suppose that
![]() $A$
is a representable algebra over the algebraic stack
$A$
is a representable algebra over the algebraic stack
![]() $X$
. Then the inertia stack of
$X$
. Then the inertia stack of
![]() $A$
is naturally identified with
$A$
is naturally identified with
![]() $A_{I_{X}}^{\text{fix}}$
. In particular,
$A_{I_{X}}^{\text{fix}}$
. In particular,
![]() $I_{A}$
is a representable algebra over
$I_{A}$
is a representable algebra over
![]() $I_{X}$
.
$I_{X}$
.
Proof. We have a commutative diagram of algebraic stacks

which identifies
![]() $I_{A}$
with a substack of
$I_{A}$
with a substack of
![]() $A|_{I_{X}}$
. The algebra
$A|_{I_{X}}$
. The algebra
![]() $A|_{I_{X}}$
is the stack of triples
$A|_{I_{X}}$
is the stack of triples
![]() $(x,\unicode[STIX]{x1D711},a)$
, where
$(x,\unicode[STIX]{x1D711},a)$
, where
![]() $x$
is an object of
$x$
is an object of
![]() $X$
,
$X$
,
![]() $\unicode[STIX]{x1D711}$
is an automorphism of
$\unicode[STIX]{x1D711}$
is an automorphism of
![]() $x$
, and
$x$
, and
![]() $a\in A(x)$
is an object of
$a\in A(x)$
is an object of
![]() $A$
lying over
$A$
lying over
![]() $x$
. Such a triple is in
$x$
. Such a triple is in
![]() $I_{A}$
if and only if
$I_{A}$
if and only if
![]() $\unicode[STIX]{x1D711}\in \operatorname{Aut}(x)$
is in the subgroup
$\unicode[STIX]{x1D711}\in \operatorname{Aut}(x)$
is in the subgroup
![]() $\operatorname{Aut}(a)\subset \operatorname{Aut}(x)$
. This is equivalent to
$\operatorname{Aut}(a)\subset \operatorname{Aut}(x)$
. This is equivalent to
![]() $\unicode[STIX]{x1D711}$
fixing
$\unicode[STIX]{x1D711}$
fixing
![]() $a$
under the action of
$a$
under the action of
![]() $\operatorname{Aut}(x)$
on
$\operatorname{Aut}(x)$
on
![]() $A(x)$
. This is the claim.◻
$A(x)$
. This is the claim.◻
In fact, the fibre of
![]() $I_{A}$
over the object
$I_{A}$
over the object
![]() $x$
of
$x$
of
![]() $X$
is equal to
$X$
is equal to
The fibre of
![]() $I_{A}(x)$
over
$I_{A}(x)$
over
![]() $\unicode[STIX]{x1D711}\in \operatorname{Aut}(x)$
is the subalgebra
$\unicode[STIX]{x1D711}\in \operatorname{Aut}(x)$
is the subalgebra
![]() $A(x)^{\unicode[STIX]{x1D711}}\subset A(x)$
, and the fibre of
$A(x)^{\unicode[STIX]{x1D711}}\subset A(x)$
, and the fibre of
![]() $I_{A}(x)$
over
$I_{A}(x)$
over
![]() $a\in A(x)$
is the subgroup
$a\in A(x)$
is the subgroup
![]() $\operatorname{Stab}_{\operatorname{Aut}(x)}(a)\subset \operatorname{Aut}(x)$
.
$\operatorname{Stab}_{\operatorname{Aut}(x)}(a)\subset \operatorname{Aut}(x)$
.
Algebra bundles
Definition 1.22. We call a finite type algebra
![]() $A\rightarrow X$
an algebra bundle if the underlying
$A\rightarrow X$
an algebra bundle if the underlying
![]() $\mathscr{O}_{X}$
-module is locally free (necessarily of finite rank).
$\mathscr{O}_{X}$
-module is locally free (necessarily of finite rank).
When studying finite type algebras over finite type stacks
![]() $X$
, we may, after passing to a locally closed stratification of
$X$
, we may, after passing to a locally closed stratification of
![]() $X$
, assume that the finite type algebra is an algebra bundle.
$X$
, assume that the finite type algebra is an algebra bundle.
Definition 1.23. Let
![]() $A\rightarrow X$
be a finite type algebra over the algebraic stack
$A\rightarrow X$
be a finite type algebra over the algebraic stack
![]() $X$
. The stratification
$X$
. The stratification
![]() $X^{\prime }\subset X$
of Proposition 1.5 is characterized by the property that an
$X^{\prime }\subset X$
of Proposition 1.5 is characterized by the property that an
![]() $X$
-scheme
$X$
-scheme
![]() $S$
factors through
$S$
factors through
![]() $X^{\prime }$
if and only if
$X^{\prime }$
if and only if
![]() $A|_{S}$
is an algebra bundle. The pullback
$A|_{S}$
is an algebra bundle. The pullback
![]() $A^{\prime }=A|_{X^{\prime }}$
is an algebra bundle, and the induced stratification
$A^{\prime }=A|_{X^{\prime }}$
is an algebra bundle, and the induced stratification
![]() $A^{\prime }\rightarrow A$
of
$A^{\prime }\rightarrow A$
of
![]() $A$
is called the rank stratification of
$A$
is called the rank stratification of
![]() $A$
.
$A$
.
Remark 1.24. By considering the representation of
![]() $A$
on itself by left multiplication, we see that every algebra bundle is a sheaf of subalgebras of the algebra
$A$
on itself by left multiplication, we see that every algebra bundle is a sheaf of subalgebras of the algebra
![]() $\operatorname{End}(V)$
of endomorphisms of a vector bundle
$\operatorname{End}(V)$
of endomorphisms of a vector bundle
![]() $V$
over the stack
$V$
over the stack
![]() $X$
.
$X$
.
Central idempotents
Lemma 1.25. The centre of an algebra bundle is a finite type algebra.
Proof. The centre of
![]() $A$
is the kernel of the
$A$
is the kernel of the
![]() $\mathscr{O}_{X}$
-linear homomorphism of vector bundles
$\mathscr{O}_{X}$
-linear homomorphism of vector bundles
![]() $A\rightarrow \operatorname{End̲}_{\mathscr{O}_{X}}(A)$
, given by
$A\rightarrow \operatorname{End̲}_{\mathscr{O}_{X}}(A)$
, given by
![]() $a\mapsto [a,\cdot \,]$
. As such, it is a locally coherent representable sheaf.◻
$a\mapsto [a,\cdot \,]$
. As such, it is a locally coherent representable sheaf.◻
Thus, if
![]() $A\rightarrow X$
is a finite type algebra over a finite type stack, after passing to a locally closed stratification of
$A\rightarrow X$
is a finite type algebra over a finite type stack, after passing to a locally closed stratification of
![]() $X$
, we may assume that
$X$
, we may assume that
![]() $A$
is an algebra bundle whose centre is an algebra bundle.
$A$
is an algebra bundle whose centre is an algebra bundle.
If
![]() $A\rightarrow X$
is a commutative algebra bundle, then
$A\rightarrow X$
is a commutative algebra bundle, then
![]() $\unicode[STIX]{x1D70B}:Y=\operatorname{Spec}_{X}A\rightarrow X$
is a finite flat representable morphism and
$\unicode[STIX]{x1D70B}:Y=\operatorname{Spec}_{X}A\rightarrow X$
is a finite flat representable morphism and
![]() $A=\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{Y}$
. In fact, the category of commutative algebra bundles over
$A=\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{Y}$
. In fact, the category of commutative algebra bundles over
![]() $X$
is equivalent to the category of finite flat representable stacks over
$X$
is equivalent to the category of finite flat representable stacks over
![]() $X$
.
$X$
.
For a commutative finite type algebra
![]() $A\rightarrow X$
, we denote the stack of idempotents in
$A\rightarrow X$
, we denote the stack of idempotents in
![]() $A$
by
$A$
by
![]() $E(A)$
.
$E(A)$
.
Lemma 1.26. Suppose
![]() $A$
is a commutative algebra bundle over the algebraic stack
$A$
is a commutative algebra bundle over the algebraic stack
![]() $X$
. Then the structure morphism
$X$
. Then the structure morphism
![]() $E(A)\rightarrow X$
is affine, of finite type, and étale. In particular, there exists a non-empty open substack
$E(A)\rightarrow X$
is affine, of finite type, and étale. In particular, there exists a non-empty open substack
![]() $U\subset X$
such that
$U\subset X$
such that
![]() $E(A)|_{U}=E(A|_{U})$
is finite étale over
$E(A)|_{U}=E(A|_{U})$
is finite étale over
![]() $U$
.
$U$
.
Proof. We reduce to the case where
![]() $X$
is a scheme and then quote Lemme 18.5.3 from [Reference Grothendieck and DieudonnéGD67, EGA IV].◻
$X$
is a scheme and then quote Lemme 18.5.3 from [Reference Grothendieck and DieudonnéGD67, EGA IV].◻
By this lemma, when studying finite type algebras over the finite type stack
![]() $X$
, we may, after passing to a stratification of
$X$
, we may, after passing to a stratification of
![]() $X$
, assume that the stack of central idempotents is finite étale over
$X$
, assume that the stack of central idempotents is finite étale over
![]() $X$
.
$X$
.
Primitive idempotents
Recall that a non-zero idempotent
![]() $e$
is called primitive if whenever
$e$
is called primitive if whenever
![]() $e=e_{1}+e_{2}$
for orthogonal idempotents
$e=e_{1}+e_{2}$
for orthogonal idempotents
![]() $e_{1}$
,
$e_{1}$
,
![]() $e_{2}$
, then necessarily
$e_{2}$
, then necessarily
![]() $e_{1}=0$
or
$e_{1}=0$
or
![]() $e_{2}=0$
.
$e_{2}=0$
.
In a finite-dimensional commutative algebra over a field, the following are true.
(i) Every idempotent is in a unique way (up to order of the summands) a sum of orthogonal primitive idempotents; this is the primitive decomposition.
(ii) Orthogonal idempotents have disjoint primitive decompositions.
(iii) Distinct primitive idempotents are orthogonal to each other.
(iv) The primitive idempotents add up to 1.
Thus, the idempotents are in bijection with the subsets of the (finite) set of primitive idempotents.
Let
![]() $A\rightarrow X$
be a finite type algebra.
$A\rightarrow X$
be a finite type algebra.
Definition 1.27. An idempotent local section
![]() $e:U\rightarrow A$
of
$e:U\rightarrow A$
of
![]() $A\rightarrow X$
is primitive if it gives rise to a primitive idempotent in the fibre of
$A\rightarrow X$
is primitive if it gives rise to a primitive idempotent in the fibre of
![]() $A$
over every geometric point of
$A$
over every geometric point of
![]() $U$
.
$U$
.
Suppose
![]() $A=\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{Y}$
is a commutative algebra bundle and
$A=\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{Y}$
is a commutative algebra bundle and
![]() $e$
an idempotent global section. Let
$e$
an idempotent global section. Let
![]() $Y_{1}\subset Y$
be the open and closed substack defined by the equation
$Y_{1}\subset Y$
be the open and closed substack defined by the equation
![]() $e=1$
. Then
$e=1$
. Then
![]() $e$
is primitive if and only if the geometric fibres of
$e$
is primitive if and only if the geometric fibres of
![]() $Y_{1}\rightarrow X$
are connected. As the function counting the number of connected components of the fibres is lower semi-continuous, the subset of
$Y_{1}\rightarrow X$
are connected. As the function counting the number of connected components of the fibres is lower semi-continuous, the subset of
![]() $X$
where
$X$
where
![]() $e$
is primitive is closed. In general, this subset is not open. Therefore, when studying primitive idempotents, we assume that
$e$
is primitive is closed. In general, this subset is not open. Therefore, when studying primitive idempotents, we assume that
![]() $E(A)\rightarrow X$
is finite étale.
$E(A)\rightarrow X$
is finite étale.
Lemma 1.28. Let
![]() $A\rightarrow X$
be a commutative algebra bundle with finite étale stack of idempotents
$A\rightarrow X$
be a commutative algebra bundle with finite étale stack of idempotents
![]() $E(A)\rightarrow X$
. There is an open and closed substack
$E(A)\rightarrow X$
. There is an open and closed substack
![]() $PE(A)\subset E(A)$
such that an idempotent local section factors through
$PE(A)\subset E(A)$
such that an idempotent local section factors through
![]() $PE(A)$
if and only if it is primitive.
$PE(A)$
if and only if it is primitive.
Proof. We may assume that
![]() $E(A)\rightarrow X$
is constant. Then the multiplication operation and the partially defined addition operation on
$E(A)\rightarrow X$
is constant. Then the multiplication operation and the partially defined addition operation on
![]() $E(A)$
are also constant. The claim follows.◻
$E(A)$
are also constant. The claim follows.◻
Definition 1.29. Let
![]() $A\rightarrow X$
be an algebra bundle with centre
$A\rightarrow X$
be an algebra bundle with centre
![]() $Z\rightarrow X$
. Let
$Z\rightarrow X$
. Let
![]() $ZE(A)$
be the stack of idempotents in
$ZE(A)$
be the stack of idempotents in
![]() $Z$
, in other words, the stack of central idempotents in
$Z$
, in other words, the stack of central idempotents in
![]() $A$
. Assume that
$A$
. Assume that
![]() $ZE(A)\rightarrow X$
is finite étale. The substack of primitive idempotents in
$ZE(A)\rightarrow X$
is finite étale. The substack of primitive idempotents in
![]() $ZE(A)$
is denoted by
$ZE(A)$
is denoted by
![]() $PZE(A)$
and called the stack of primitive central idempotents of
$PZE(A)$
and called the stack of primitive central idempotents of
![]() $A$
. It is finite étale over
$A$
. It is finite étale over
![]() $X$
. The degree of
$X$
. The degree of
![]() $PZE(A)\rightarrow X$
is called the central rank of
$PZE(A)\rightarrow X$
is called the central rank of
![]() $A$
.
$A$
.
If
![]() $X$
is connected, the number of connected components of
$X$
is connected, the number of connected components of
![]() $PZE(A)$
is the split central rank of
$PZE(A)$
is the split central rank of
![]() $A$
. More precisely, the partition of the central rank given by the degrees of the connected components of
$A$
. More precisely, the partition of the central rank given by the degrees of the connected components of
![]() $PZE(A)$
is called the central type of
$PZE(A)$
is called the central type of
![]() $A$
. (So the split central rank is the length of the type.)
$A$
. (So the split central rank is the length of the type.)
Remark 1.30. Let
![]() $X$
be connected, and let
$X$
be connected, and let
![]() $A\rightarrow X$
be a commutative finite type algebra with finite étale stack of idempotents
$A\rightarrow X$
be a commutative finite type algebra with finite étale stack of idempotents
![]() $E(A)\rightarrow X$
. Then there is a one-to-one correspondence between the connected components of
$E(A)\rightarrow X$
. Then there is a one-to-one correspondence between the connected components of
![]() $PE(A)$
and the primitive idempotents in the algebra of global sections
$PE(A)$
and the primitive idempotents in the algebra of global sections
![]() $\unicode[STIX]{x1D6E4}(X,A)$
.
$\unicode[STIX]{x1D6E4}(X,A)$
.
The degree stratification
Let
![]() $k$
be a field and
$k$
be a field and
![]() $A$
a finite-dimensional
$A$
a finite-dimensional
![]() $k$
-algebra. The rank
$k$
-algebra. The rank
![]() $r$
of
$r$
of
![]() $A$
is the dimension of
$A$
is the dimension of
![]() $A$
as a
$A$
as a
![]() $k$
-vector space. For an element
$k$
-vector space. For an element
![]() $a\in A$
, we define its degree to be the dimension of the commutative subalgebra
$a\in A$
, we define its degree to be the dimension of the commutative subalgebra
![]() $k[a]\subset A$
. It is equal to the degree of the minimal polynomial of
$k[a]\subset A$
. It is equal to the degree of the minimal polynomial of
![]() $a$
, i.e., the monic generator of the kernel of the algebra map
$a$
, i.e., the monic generator of the kernel of the algebra map
![]() $k[x]\rightarrow A$
, defined by
$k[x]\rightarrow A$
, defined by
![]() $x\mapsto a$
.
$x\mapsto a$
.
Now let
![]() $A$
be an algebra bundle of rank
$A$
be an algebra bundle of rank
![]() $r$
over the algebraic stack
$r$
over the algebraic stack
![]() $X$
, and
$X$
, and
![]() $a\in A(S)$
a local section of
$a\in A(S)$
a local section of
![]() $A$
over an
$A$
over an
![]() $X$
-scheme
$X$
-scheme
![]() $S$
.
$S$
.
Definition 1.31. If the cokernel (as a homomorphism of
![]() $\mathscr{O}_{S}$
-modules) of the morphism of
$\mathscr{O}_{S}$
-modules) of the morphism of
![]() $\mathscr{O}_{S}$
-algebras
$\mathscr{O}_{S}$
-algebras
![]() $\mathscr{O}_{S}[x]\rightarrow A_{S}$
defined by
$\mathscr{O}_{S}[x]\rightarrow A_{S}$
defined by
![]() $x\mapsto a$
is flat over
$x\mapsto a$
is flat over
![]() $\mathscr{O}_{S}$
, we say that
$\mathscr{O}_{S}$
, we say that
![]() $a$
is strict, and we call the rank of the image of
$a$
is strict, and we call the rank of the image of
![]() $\mathscr{O}_{S}[x]\rightarrow A$
the degree of
$\mathscr{O}_{S}[x]\rightarrow A$
the degree of
![]() $a$
.
$a$
.
If
![]() $f(x)\in \mathscr{O}_{S}[x]$
is the characteristic polynomial of
$f(x)\in \mathscr{O}_{S}[x]$
is the characteristic polynomial of
![]() $a$
, the morphism
$a$
, the morphism
![]() $\mathscr{O}_{S}[x]\rightarrow A$
factors through
$\mathscr{O}_{S}[x]\rightarrow A$
factors through
![]() $\mathscr{O}_{S}[x]/(f)$
, by the theorem of Caley–Hamilton. Hence, the cokernel of
$\mathscr{O}_{S}[x]/(f)$
, by the theorem of Caley–Hamilton. Hence, the cokernel of
![]() $\mathscr{O}_{S}[x]\rightarrow A$
is actually a cokernel of a homomorphism of vector bundles and hence coherent. The condition that this cokernel be flat is equivalent to it being locally free. It implies that forming the image of
$\mathscr{O}_{S}[x]\rightarrow A$
is actually a cokernel of a homomorphism of vector bundles and hence coherent. The condition that this cokernel be flat is equivalent to it being locally free. It implies that forming the image of
![]() $\mathscr{O}_{S}[x]\rightarrow A$
commutes with base change, and that this image, denoted by
$\mathscr{O}_{S}[x]\rightarrow A$
commutes with base change, and that this image, denoted by
![]() $\mathscr{O}_{S}[a]$
, is also locally free.
$\mathscr{O}_{S}[a]$
, is also locally free.
Proposition 1.32. For every
![]() $n=1,\ldots ,r$
, there exists a locally closed substack
$n=1,\ldots ,r$
, there exists a locally closed substack
![]() $A_{n}\subset A$
with the property that a local section
$A_{n}\subset A$
with the property that a local section
![]() $a\in A(S)$
factors through
$a\in A(S)$
factors through
![]() $A_{n}(S)$
if and only if
$A_{n}(S)$
if and only if
![]() $a$
is strict of degree
$a$
is strict of degree
![]() $n$
. The
$n$
. The
![]() $A_{n}$
are pairwise disjoint and their disjoint union
$A_{n}$
are pairwise disjoint and their disjoint union
maps surjectively to
![]() $A$
. The section
$A$
. The section
![]() $a\in A(S)$
factors through
$a\in A(S)$
factors through
![]() $A^{\text{strat}}\rightarrow A$
if and only if it is strict.
$A^{\text{strat}}\rightarrow A$
if and only if it is strict.
Proof. Consider the tautological section
![]() $\unicode[STIX]{x1D6E5}$
of the pullback of
$\unicode[STIX]{x1D6E5}$
of the pullback of
![]() $A$
via the structure map
$A$
via the structure map
![]() $A\rightarrow X$
. It gives rise to a morphism of
$A\rightarrow X$
. It gives rise to a morphism of
![]() $\mathscr{O}_{A}$
-algebras
$\mathscr{O}_{A}$
-algebras
![]() $\mathscr{O}_{A}[x]\rightarrow A_{A}$
. Then
$\mathscr{O}_{A}[x]\rightarrow A_{A}$
. Then
![]() $A^{\text{strat}}$
is given by the flattening stratification of its cokernel, and
$A^{\text{strat}}$
is given by the flattening stratification of its cokernel, and
![]() $A_{n}\subset A^{\text{strat}}$
is the component where the cokernel has rank
$A_{n}\subset A^{\text{strat}}$
is the component where the cokernel has rank
![]() $r-n$
.◻
$r-n$
.◻
We call the stratification
![]() $A^{\text{strat}}\rightarrow A$
the degree stratification of
$A^{\text{strat}}\rightarrow A$
the degree stratification of
![]() $A$
.
$A$
.
Semi-simple elements
Let
![]() $k$
be an algebraically closed field and
$k$
be an algebraically closed field and
![]() $A$
a finite-dimensional
$A$
a finite-dimensional
![]() $k$
-algebra. Recall that an element
$k$
-algebra. Recall that an element
![]() $a\in A$
is semi-simple if the following equivalent conditions are satisfied.
$a\in A$
is semi-simple if the following equivalent conditions are satisfied.
(i) The map
 $A\rightarrow A$
given by left multiplication by
$A\rightarrow A$
given by left multiplication by
 $a$
is diagonalizable.
$a$
is diagonalizable.(ii) The minimal polynomial
 $f\in k[x]$
of
$f\in k[x]$
of
 $a$
is separable, i.e., satisfies
$a$
is separable, i.e., satisfies
 $(f,f^{\prime })=1$
.
$(f,f^{\prime })=1$
.(iii) The commutative subalgebra
 $k[a]\subset A$
is reduced, or, equivalently, étale over
$k[a]\subset A$
is reduced, or, equivalently, étale over
 $k$
.
$k$
.
Definition 1.33. Let
![]() $A\rightarrow X$
be an algebra bundle. A local section
$A\rightarrow X$
be an algebra bundle. A local section
![]() $a\in A(S)$
, for an
$a\in A(S)$
, for an
![]() $X$
-scheme
$X$
-scheme
![]() $S$
, is called semi-simple if it is strict and for every geometric point
$S$
, is called semi-simple if it is strict and for every geometric point
![]() $s\in S$
, the element induced by
$s\in S$
, the element induced by
![]() $a$
in
$a$
in
![]() $A(s)$
is semi-simple.
$A(s)$
is semi-simple.
For example, an idempotent section
![]() $e\in A(S)$
is semi-simple over the open subset of
$e\in A(S)$
is semi-simple over the open subset of
![]() $S$
, where
$S$
, where
![]() $e$
is neither 0 nor 1 (in a commutative algebra bundle, this subset is also closed).
$e$
is neither 0 nor 1 (in a commutative algebra bundle, this subset is also closed).
Assuming
![]() $a\in A(S)$
is strict,
$a\in A(S)$
is strict,
![]() $a$
is semi-simple if and only if the geometric fibres of the finite flat
$a$
is semi-simple if and only if the geometric fibres of the finite flat
![]() $S$
-scheme
$S$
-scheme
![]() $\operatorname{Spec}_{S}\mathscr{O}_{S}[a]$
are unramified. This condition is equivalent to
$\operatorname{Spec}_{S}\mathscr{O}_{S}[a]$
are unramified. This condition is equivalent to
![]() $\operatorname{Spec}_{S}\mathscr{O}_{S}[a]$
being unramified and hence étale over
$\operatorname{Spec}_{S}\mathscr{O}_{S}[a]$
being unramified and hence étale over
![]() $S$
.
$S$
.
The semi-simple sections of
![]() $A$
form a subsheaf
$A$
form a subsheaf
![]() $A^{\text{ss}}\subset A$
.
$A^{\text{ss}}\subset A$
.
Proposition 1.34. Let
![]() $A\rightarrow X$
be an algebra bundle over the algebraic stack
$A\rightarrow X$
be an algebra bundle over the algebraic stack
![]() $X$
. Then
$X$
. Then
![]() $A^{\text{ss}}$
is an algebraic stack with a representable structure morphism of finite type
$A^{\text{ss}}$
is an algebraic stack with a representable structure morphism of finite type
![]() $A^{\text{ss}}\rightarrow X$
.
$A^{\text{ss}}\rightarrow X$
.
Proof. In fact,
![]() $A^{\text{ss}}\subset A^{\text{strat}}$
is the open substack defined by the condition that the finite flat representable morphism
$A^{\text{ss}}\subset A^{\text{strat}}$
is the open substack defined by the condition that the finite flat representable morphism
![]() $\operatorname{Spec}_{A}\mathscr{O}_{A}[\unicode[STIX]{x1D6E5}]\rightarrow A$
is unramified. (The section
$\operatorname{Spec}_{A}\mathscr{O}_{A}[\unicode[STIX]{x1D6E5}]\rightarrow A$
is unramified. (The section
![]() $\unicode[STIX]{x1D6E5}$
is the tautological one, as in the proof of Proposition 1.32.) Thus, we have a factorization of the monomorphism
$\unicode[STIX]{x1D6E5}$
is the tautological one, as in the proof of Proposition 1.32.) Thus, we have a factorization of the monomorphism
![]() $A^{\text{ss}}\rightarrow A$
as
$A^{\text{ss}}\rightarrow A$
as
Thus,
![]() $A^{\text{ss}}\subset A$
is a constructible substack.◻
$A^{\text{ss}}\subset A$
is a constructible substack.◻
The semi-simple centre
For a commutative finite-dimensional algebra over an algebraically closed field, we have the following facts.
(i) The primitive idempotents are linearly independent.
(ii) An element is semi-simple if and only if it is a linear combination of primitive idempotents.
We need a version of this statement for algebra bundles.
Proposition 1.35. Let
![]() $A\rightarrow X$
be a commutative algebra bundle whose stack of idempotents is finite étale, and let
$A\rightarrow X$
be a commutative algebra bundle whose stack of idempotents is finite étale, and let
![]() $Y\rightarrow X$
be the finite flat cover corresponding to
$Y\rightarrow X$
be the finite flat cover corresponding to
![]() $A$
. There is a canonical finite flat morphism of
$A$
. There is a canonical finite flat morphism of
![]() $X$
-stacks
$X$
-stacks
![]() $Y\rightarrow PE(A)$
. Over every geometric point
$Y\rightarrow PE(A)$
. Over every geometric point
![]() $x$
of
$x$
of
![]() $X$
, this morphism maps each point in the fibre
$X$
, this morphism maps each point in the fibre
![]() $Y_{x}$
to the characteristic function of its connected component in
$Y_{x}$
to the characteristic function of its connected component in
![]() $Y_{x}$
(which is a primitive idempotent in
$Y_{x}$
(which is a primitive idempotent in
![]() $A|_{x}$
). Dually, we obtain a strict monomorphism of algebra bundles
$A|_{x}$
). Dually, we obtain a strict monomorphism of algebra bundles
where
![]() $\unicode[STIX]{x1D70B}:PE(A)\rightarrow X$
is the structure map.
$\unicode[STIX]{x1D70B}:PE(A)\rightarrow X$
is the structure map.
The induced morphism
factors through the open substack
![]() $A^{\text{ss}}\subset A^{\text{strat}}$
and induces a surjective closed immersion of algebraic stacks
$A^{\text{ss}}\subset A^{\text{strat}}$
and induces a surjective closed immersion of algebraic stacks
![]() $(\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{PE(A)})^{\text{strat}}\rightarrow A^{\text{ss}}$
.
$(\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{PE(A)})^{\text{strat}}\rightarrow A^{\text{ss}}$
.
Proof. Consider the finite étale cover of primitive idempotents
![]() $\unicode[STIX]{x1D70B}:PE(A)\rightarrow X$
. We have a tautological global section
$\unicode[STIX]{x1D70B}:PE(A)\rightarrow X$
. We have a tautological global section
![]() $e$
of
$e$
of
![]() $A|_{PE(A)}$
, and
$A|_{PE(A)}$
, and
![]() $a\mapsto ae$
defines a homomorphism of
$a\mapsto ae$
defines a homomorphism of
![]() $\mathscr{O}_{PE(A)}$
-modules
$\mathscr{O}_{PE(A)}$
-modules
![]() $\mathscr{O}_{PE(A)}\rightarrow A|_{PE(A)}$
. Pushing forward with
$\mathscr{O}_{PE(A)}\rightarrow A|_{PE(A)}$
. Pushing forward with
![]() $\unicode[STIX]{x1D70B}$
and composing with the trace map
$\unicode[STIX]{x1D70B}$
and composing with the trace map
![]() $\unicode[STIX]{x1D70B}_{\ast }(A|_{PE(A)})\rightarrow A$
defines the morphism of algebra bundles over
$\unicode[STIX]{x1D70B}_{\ast }(A|_{PE(A)})\rightarrow A$
defines the morphism of algebra bundles over
![]() $X$
,
$X$
,
It is a strict monomorphism of vector bundles, because it is injective over every geometric point, by fact (i), above. Dually, we obtain a morphism of
![]() $X$
-stacks
$X$
-stacks
![]() $Y\rightarrow PE(A)$
, which is the morphism described in the statement of the proposition. It is flat, because
$Y\rightarrow PE(A)$
, which is the morphism described in the statement of the proposition. It is flat, because
![]() $PE(A)$
is étale over
$PE(A)$
is étale over
![]() $X$
, and flatness can be checked étale locally.
$X$
, and flatness can be checked étale locally.
Passing to the degree stratification commutes with strict monomorphisms of algebra bundles, so we have a cartesian diagram of
![]() $X$
-stacks
$X$
-stacks

which shows that
![]() $(\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{PE(A)})^{\text{strat}}\rightarrow A^{\text{strat}}$
is a closed immersion. That this closed immersion factors through
$(\unicode[STIX]{x1D70B}_{\ast }\mathscr{O}_{PE(A)})^{\text{strat}}\rightarrow A^{\text{strat}}$
is a closed immersion. That this closed immersion factors through
![]() $A^{\text{ss}}\subset A^{\text{strat}}$
and is surjective onto
$A^{\text{ss}}\subset A^{\text{strat}}$
and is surjective onto
![]() $A^{\text{ss}}$
can be checked over the geometric points of
$A^{\text{ss}}$
can be checked over the geometric points of
![]() $X$
, where it follows from fact (ii), above.◻
$X$
, where it follows from fact (ii), above.◻
Permanence of rank and split rank
Proposition 1.36. Let
![]() $A{\hookrightarrow}A^{\prime }$
be a monomorphism of commutative finite type algebras with finite étale stacks of idempotents over the connected stack
$A{\hookrightarrow}A^{\prime }$
be a monomorphism of commutative finite type algebras with finite étale stacks of idempotents over the connected stack
![]() $X$
. Denote the ranks of
$X$
. Denote the ranks of
![]() $A$
and
$A$
and
![]() $A^{\prime }$
by
$A^{\prime }$
by
![]() $n$
and
$n$
and
![]() $n^{\prime }$
, and the split ranks by
$n^{\prime }$
, and the split ranks by
![]() $k$
and
$k$
and
![]() $k^{\prime }$
, respectively. Then
$k^{\prime }$
, respectively. Then
![]() $n\leqslant n^{\prime }$
and
$n\leqslant n^{\prime }$
and
![]() $k\leqslant k^{\prime }$
. Moreover:
$k\leqslant k^{\prime }$
. Moreover:
(i) if
 $A^{\prime }$
admits a semi-simple global section that does not factor through the fibre
$A^{\prime }$
admits a semi-simple global section that does not factor through the fibre
 $A|_{x}$
for all points of
$A|_{x}$
for all points of
 $x$
, then
$x$
, then
 $n<n^{\prime }$
;
$n<n^{\prime }$
;(ii) if
 $A^{\prime }$
admits an idempotent global section that is not in
$A^{\prime }$
admits an idempotent global section that is not in
 $A$
, then
$A$
, then
 $k<k^{\prime }$
.
$k<k^{\prime }$
.
Proof. The monomorphism
![]() $A{\hookrightarrow}A^{\prime }$
induces an open and closed embedding of finite étale
$A{\hookrightarrow}A^{\prime }$
induces an open and closed embedding of finite étale
![]() $X$
-stacks
$X$
-stacks
![]() $E(A){\hookrightarrow}E(A^{\prime })$
. Every idempotent
$E(A){\hookrightarrow}E(A^{\prime })$
. Every idempotent
![]() $e$
in
$e$
in
![]() $A$
can be decomposed uniquely into a sum of orthogonal primitive idempotents in
$A$
can be decomposed uniquely into a sum of orthogonal primitive idempotents in
![]() $A^{\prime }$
. Let us call this the primitive decomposition of
$A^{\prime }$
. Let us call this the primitive decomposition of
![]() $e$
in
$e$
in
![]() $A^{\prime }$
. Consider the correspondence
$A^{\prime }$
. Consider the correspondence
![]() $Q\subset PE(A)\times _{X}PE(A^{\prime })$
defined by
$Q\subset PE(A)\times _{X}PE(A^{\prime })$
defined by
One shows that
![]() $Q$
is a finite étale cover of
$Q$
is a finite étale cover of
![]() $X$
locally in the étale topology of
$X$
locally in the étale topology of
![]() $X$
, reducing to the case where both
$X$
, reducing to the case where both
![]() $E(A)$
and
$E(A)$
and
![]() $E(A^{\prime })$
are trivial covers. By properties of the primitive decomposition, the projection
$E(A^{\prime })$
are trivial covers. By properties of the primitive decomposition, the projection
![]() $Q\rightarrow PE(A)$
is surjective and the projection
$Q\rightarrow PE(A)$
is surjective and the projection
![]() $Q\rightarrow PE(A^{\prime })$
is injective. Thus, we have
$Q\rightarrow PE(A^{\prime })$
is injective. Thus, we have
If
![]() $n=n^{\prime }$
, then both
$n=n^{\prime }$
, then both
![]() $Q\rightarrow PE(A)$
and
$Q\rightarrow PE(A)$
and
![]() $Q\rightarrow PE(A^{\prime })$
are isomorphisms, showing that
$Q\rightarrow PE(A^{\prime })$
are isomorphisms, showing that
![]() $PE(A)=PE(A^{\prime })$
. By Proposition 1.35, this implies that the morphism
$PE(A)=PE(A^{\prime })$
. By Proposition 1.35, this implies that the morphism
![]() $A^{\text{ss}}\rightarrow (A^{\prime })^{\text{ss}}$
is surjective. This proves (i).
$A^{\text{ss}}\rightarrow (A^{\prime })^{\text{ss}}$
is surjective. This proves (i).
We can repeat the argument for the algebras of global sections
![]() $\unicode[STIX]{x1D6E4}(X,A){\hookrightarrow}\unicode[STIX]{x1D6E4}(X,A^{\prime })$
. We deduce that
$\unicode[STIX]{x1D6E4}(X,A){\hookrightarrow}\unicode[STIX]{x1D6E4}(X,A^{\prime })$
. We deduce that
![]() $k\leqslant k^{\prime }$
, and if
$k\leqslant k^{\prime }$
, and if
![]() $k=k^{\prime }$
, every primitive idempotent in
$k=k^{\prime }$
, every primitive idempotent in
![]() $\unicode[STIX]{x1D6E4}(X,A)$
remains primitive in
$\unicode[STIX]{x1D6E4}(X,A)$
remains primitive in
![]() $\unicode[STIX]{x1D6E4}(X,A^{\prime })$
and every primitive idempotent of
$\unicode[STIX]{x1D6E4}(X,A^{\prime })$
and every primitive idempotent of
![]() $\unicode[STIX]{x1D6E4}(X,A^{\prime })$
is in
$\unicode[STIX]{x1D6E4}(X,A^{\prime })$
is in
![]() $\unicode[STIX]{x1D6E4}(X,A)$
. We deduce that
$\unicode[STIX]{x1D6E4}(X,A)$
. We deduce that
![]() $\unicode[STIX]{x1D6E4}(X,A)$
and
$\unicode[STIX]{x1D6E4}(X,A)$
and
![]() $\unicode[STIX]{x1D6E4}(X,A^{\prime })$
have the same idempotents, which proves (ii).◻
$\unicode[STIX]{x1D6E4}(X,A^{\prime })$
have the same idempotents, which proves (ii).◻
Families of idempotents
Definition 1.37. For a finite type algebra
![]() $A\rightarrow X$
, we denote by
$A\rightarrow X$
, we denote by
![]() $E_{n}(A)\rightarrow X$
the stack of
$E_{n}(A)\rightarrow X$
the stack of
![]() $n$
-tuples of non-zero idempotents in
$n$
-tuples of non-zero idempotents in
![]() $A$
that are pairwise orthogonal and add up to unity. We call sections of
$A$
that are pairwise orthogonal and add up to unity. We call sections of
![]() $E_{n}(A)$
also complete sets of orthogonal idempotents.
$E_{n}(A)$
also complete sets of orthogonal idempotents.
Note that the family members of the sections of
![]() $E_{n}(A)$
need not be central.
$E_{n}(A)$
need not be central.
The stack
![]() $E_{n}(A)$
is algebraic and of finite type over
$E_{n}(A)$
is algebraic and of finite type over
![]() $X$
.
$X$
.
For
![]() $n=0$
, the stack
$n=0$
, the stack
![]() $E_{0}(A)$
is empty, unless
$E_{0}(A)$
is empty, unless
![]() $A=0$
, in which case it is identified with
$A=0$
, in which case it is identified with
![]() $X$
. For
$X$
. For
![]() $n=1$
, the stack
$n=1$
, the stack
![]() $E_{1}(A)$
contains exactly the unit in
$E_{1}(A)$
contains exactly the unit in
![]() $A$
(so is identified with
$A$
(so is identified with
![]() $X$
), unless
$X$
), unless
![]() $A=0$
, in which case
$A=0$
, in which case
![]() $E_{1}(A)$
is empty.
$E_{1}(A)$
is empty.
Group of units
Let
![]() $A\rightarrow X$
be a finite type algebra over the algebraic stack
$A\rightarrow X$
be a finite type algebra over the algebraic stack
![]() $X$
. The subsheaf of units
$X$
. The subsheaf of units
![]() $A^{\times }\subset A$
is defined by
$A^{\times }\subset A$
is defined by
for every object
![]() $x$
of
$x$
of
![]() $X$
. We can see that
$X$
. We can see that
![]() $A^{\times }$
is a (relative) affine group scheme over
$A^{\times }$
is a (relative) affine group scheme over
![]() $X$
by writing it as the fibred product, as shown in the following diagram.
$X$
by writing it as the fibred product, as shown in the following diagram.

If
![]() $A$
is an algebra bundle, the subsheaf
$A$
is an algebra bundle, the subsheaf
![]() $A^{\times }\subset A$
is represented by an open substack, because in this case, a local section
$A^{\times }\subset A$
is represented by an open substack, because in this case, a local section
![]() $a$
is invertible if and only if the determinants of left and right multiplication by
$a$
is invertible if and only if the determinants of left and right multiplication by
![]() $a$
on
$a$
on
![]() $A$
do not vanish. We conclude that if
$A$
do not vanish. We conclude that if
![]() $A$
is an algebra bundle,
$A$
is an algebra bundle,
![]() $A^{\times }$
is smooth over
$A^{\times }$
is smooth over
![]() $X$
with geometrically connected fibres. For the general case, this still implies that the fibres of
$X$
with geometrically connected fibres. For the general case, this still implies that the fibres of
![]() $A^{\times }\rightarrow X$
are smooth and geometrically connected, as the fibres do not change when passing to a stratification of
$A^{\times }\rightarrow X$
are smooth and geometrically connected, as the fibres do not change when passing to a stratification of
![]() $X$
.
$X$
.
A similar argument using the determinant proves that if
![]() $A\rightarrow B$
is a strict monomorphism of algebra bundles, we have
$A\rightarrow B$
is a strict monomorphism of algebra bundles, we have
![]() $A^{\times }=A\cap B^{\times }$
. Also, if
$A^{\times }=A\cap B^{\times }$
. Also, if
![]() $A$
is an algebra bundle, any morphism
$A$
is an algebra bundle, any morphism
![]() $A\rightarrow B$
to another algebra bundle is determined by its restriction to
$A\rightarrow B$
to another algebra bundle is determined by its restriction to
![]() $A^{\times }$
.
$A^{\times }$
.
1.4 Algebroids
Definition 1.38. An algebroid is a triple
![]() $(X,A,\unicode[STIX]{x1D704})$
, where
$(X,A,\unicode[STIX]{x1D704})$
, where
![]() $X$
is an algebraic stack,
$X$
is an algebraic stack,
![]() $A$
is a finite type algebra over
$A$
is a finite type algebra over
![]() $X$
, and
$X$
, and
![]() $\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is a homomorphism of sheaves of groups over
$\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is a homomorphism of sheaves of groups over
![]() $X$
, which identifies
$X$
, which identifies
![]() $A^{\times }$
with an open substack of
$A^{\times }$
with an open substack of
![]() $I_{X}$
. Moreover, we require that the diagram
$I_{X}$
. Moreover, we require that the diagram

of groups over
![]() $X$
commutes. Here, the map
$X$
commutes. Here, the map
![]() $A^{\times }\rightarrow \operatorname{Aut̲}_{X}(A)$
associates to a unit
$A^{\times }\rightarrow \operatorname{Aut̲}_{X}(A)$
associates to a unit
![]() $u$
of
$u$
of
![]() $A$
the inner automorphism
$A$
the inner automorphism
![]() $x\mapsto uxu^{-1}$
. The vertical map
$x\mapsto uxu^{-1}$
. The vertical map
![]() $I_{X}\rightarrow \operatorname{Aut̲}_{X}(A)$
is the inertia representation (6). If
$I_{X}\rightarrow \operatorname{Aut̲}_{X}(A)$
is the inertia representation (6). If
![]() $\unicode[STIX]{x1D704}$
is an isomorphism, we call
$\unicode[STIX]{x1D704}$
is an isomorphism, we call
![]() $(X,A,\unicode[STIX]{x1D704})$
a strict algebroid.
$(X,A,\unicode[STIX]{x1D704})$
a strict algebroid.
We will usually abbreviate the triple
![]() $(X,A,\unicode[STIX]{x1D704})$
to
$(X,A,\unicode[STIX]{x1D704})$
to
![]() $X$
and write
$X$
and write
![]() $A_{X}$
for
$A_{X}$
for
![]() $A$
if we need to specify the algebra. We call the commutativity of (7) the algebroid property.
$A$
if we need to specify the algebra. We call the commutativity of (7) the algebroid property.
For an explanation of the terminology, see Remark 1.44.
The condition that
![]() $\unicode[STIX]{x1D704}$
is an open immersion implies that
$\unicode[STIX]{x1D704}$
is an open immersion implies that
![]() $A^{\times }$
represents the subsheaf
$A^{\times }$
represents the subsheaf
![]() $I_{X}^{\circ }\subset I_{X}$
of connected components of the identity. (Over a field,
$I_{X}^{\circ }\subset I_{X}$
of connected components of the identity. (Over a field,
![]() $A^{\times }$
is connected, and
$A^{\times }$
is connected, and
![]() $A^{\times }\rightarrow I_{X}$
being an open immersion implies that
$A^{\times }\rightarrow I_{X}$
being an open immersion implies that
![]() $I_{X}/A^{\times }$
is étale. These conditions characterize the connected component over a field.) In particular, if
$I_{X}/A^{\times }$
is étale. These conditions characterize the connected component over a field.) In particular, if
![]() $X$
is a connected gerbe over a Deligne–Mumford stack
$X$
is a connected gerbe over a Deligne–Mumford stack
![]() $S$
, then the relative inertia
$S$
, then the relative inertia
![]() $I_{X/S}$
is necessarily equal to
$I_{X/S}$
is necessarily equal to
![]() $I_{X}^{\circ }$
, and hence
$I_{X}^{\circ }$
, and hence
![]() $A^{\times }$
is identified with
$A^{\times }$
is identified with
![]() $I_{X/S}$
.
$I_{X/S}$
.
If
![]() $A$
is an algebra bundle,
$A$
is an algebra bundle,
![]() $A^{\times }$
, and therefore also
$A^{\times }$
, and therefore also
![]() $I_{X}^{\circ }$
, is an affine smooth (relative) group scheme over
$I_{X}^{\circ }$
, is an affine smooth (relative) group scheme over
![]() $X$
. Hence,
$X$
. Hence,
![]() $X$
admits a coarse Deligne–Mumford stack
$X$
admits a coarse Deligne–Mumford stack
![]() $X\rightarrow \overline{X}$
, which is uniquely determined by being a Deligne–Mumford stack and
$X\rightarrow \overline{X}$
, which is uniquely determined by being a Deligne–Mumford stack and
![]() $X\rightarrow \overline{X}$
being a connected gerbe. Moreover,
$X\rightarrow \overline{X}$
being a connected gerbe. Moreover,
![]() $A^{\times }$
is then identified with the relative inertia group
$A^{\times }$
is then identified with the relative inertia group
![]() $I_{X/\overline{X}}\subset I_{X}$
, and we have a short exact sequence of relative group schemes
$I_{X/\overline{X}}\subset I_{X}$
, and we have a short exact sequence of relative group schemes
over
![]() $X$
. In the case where
$X$
. In the case where
![]() $(X,A)$
is a strict algebroid,
$(X,A)$
is a strict algebroid,
![]() $I_{X}^{\circ }=I_{X}$
and
$I_{X}^{\circ }=I_{X}$
and
![]() $\overline{X}$
is an algebraic space, in fact the coarse moduli space of
$\overline{X}$
is an algebraic space, in fact the coarse moduli space of
![]() $X$
.
$X$
.
In many cases, the algebroid property is automatic.
Proposition 1.39. Consider a triple
![]() $(X,A,\unicode[STIX]{x1D704})$
, where
$(X,A,\unicode[STIX]{x1D704})$
, where
![]() $X$
is an algebraic stack,
$X$
is an algebraic stack,
![]() $A$
is an algebra bundle over
$A$
is an algebra bundle over
![]() $X$
, and
$X$
, and
![]() $\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is a homomorphism of sheaves of groups over
$\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is a homomorphism of sheaves of groups over
![]() $X$
that identifies
$X$
that identifies
![]() $A^{\times }$
with an open substack of
$A^{\times }$
with an open substack of
![]() $I_{X}$
. Then (7) commutes, so
$I_{X}$
. Then (7) commutes, so
![]() $(X,A,\unicode[STIX]{x1D704})$
is an algebroid.
$(X,A,\unicode[STIX]{x1D704})$
is an algebroid.
Proof. As
![]() $\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is defined over
$\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
is defined over
![]() $X$
, the homomorphism
$X$
, the homomorphism
![]() $\unicode[STIX]{x1D704}$
is equivariant with respect to the inertia action. The proof now combines the facts that
$\unicode[STIX]{x1D704}$
is equivariant with respect to the inertia action. The proof now combines the facts that
![]() $\unicode[STIX]{x1D704}$
is a monomorphism, that the inertia action on
$\unicode[STIX]{x1D704}$
is a monomorphism, that the inertia action on
![]() $I_{X}$
is the inner action, and that a morphism of algebra bundles is determined by its restriction to units.
$I_{X}$
is the inner action, and that a morphism of algebra bundles is determined by its restriction to units.
In fact, let
![]() $a\in A^{\times }$
. To show that
$a\in A^{\times }$
. To show that
![]() $^{a}(\cdot )=\unicode[STIX]{x1D704}(a)\cdot$
, as automorphism of
$^{a}(\cdot )=\unicode[STIX]{x1D704}(a)\cdot$
, as automorphism of
![]() $A$
, it suffices to show that for all
$A$
, it suffices to show that for all
![]() $b\in A^{\times }$
we have
$b\in A^{\times }$
we have
![]() $^{a}b=\unicode[STIX]{x1D704}(a)\cdot b$
. We can check this after applying
$^{a}b=\unicode[STIX]{x1D704}(a)\cdot b$
. We can check this after applying
![]() $\unicode[STIX]{x1D704}$
, so it suffices that
$\unicode[STIX]{x1D704}$
, so it suffices that
![]() $\unicode[STIX]{x1D704}(\text{}^{a}b)=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D704}(a)\cdot b)$
, or
$\unicode[STIX]{x1D704}(\text{}^{a}b)=\unicode[STIX]{x1D704}(\unicode[STIX]{x1D704}(a)\cdot b)$
, or
![]() $^{\unicode[STIX]{x1D704}(a)}\unicode[STIX]{x1D704}(b)=\unicode[STIX]{x1D704}(a)\cdot \unicode[STIX]{x1D704}(b)$
, which is true.◻
$^{\unicode[STIX]{x1D704}(a)}\unicode[STIX]{x1D704}(b)=\unicode[STIX]{x1D704}(a)\cdot \unicode[STIX]{x1D704}(b)$
, which is true.◻
Example 1.40 (Algebroid underlying a linear stack).
Let
![]() $\mathfrak{X}$
be a linear algebraic stack with underlying algebraic stack
$\mathfrak{X}$
be a linear algebraic stack with underlying algebraic stack
![]() $X$
, and let
$X$
, and let
![]() $A\rightarrow X$
be the universal sheaf of endomorphisms of Remark 1.10. Then automorphisms are invertible endomorphisms, so we use for
$A\rightarrow X$
be the universal sheaf of endomorphisms of Remark 1.10. Then automorphisms are invertible endomorphisms, so we use for
![]() $\unicode[STIX]{x1D704}$
the tautological identification
$\unicode[STIX]{x1D704}$
the tautological identification
![]() $A^{\times }=I_{X}$
.
$A^{\times }=I_{X}$
.
The inertia representation being the inverse of the pullback action, it is, indeed, given by (left) inner automorphisms.
We call
![]() $(X,A)$
the algebroid underlying the linear algebraic stack
$(X,A)$
the algebroid underlying the linear algebraic stack
![]() $\mathfrak{X}$
. It is a strict algebroid.
$\mathfrak{X}$
. It is a strict algebroid.
Example 1.41. Consider the linear stack of vector bundles
![]() $\mathfrak{Vect}$
, as in Example 1.12. The underlying algebroid consists of the disjoint union of the quotient stacks
$\mathfrak{Vect}$
, as in Example 1.12. The underlying algebroid consists of the disjoint union of the quotient stacks
![]() $\operatorname{GL}_{n}\backslash M_{n\times n}$
, given by the adjoint representations, for
$\operatorname{GL}_{n}\backslash M_{n\times n}$
, given by the adjoint representations, for
![]() $n\geqslant 0$
. Thus, in passing from the linear stack to the underlying algebroid, we discard all
$n\geqslant 0$
. Thus, in passing from the linear stack to the underlying algebroid, we discard all
![]() $M_{m\times n}$
for
$M_{m\times n}$
for
![]() $m\not =n$
, and for
$m\not =n$
, and for
![]() $m=n$
we restrict the left-right bi-action of
$m=n$
we restrict the left-right bi-action of
![]() $\operatorname{GL}_{n}$
on
$\operatorname{GL}_{n}$
on
![]() $M_{n\times n}$
to the (left only) adjoint action. Thus, we remove exactly the information which we consider non-local, see Remark 1.15.
$M_{n\times n}$
to the (left only) adjoint action. Thus, we remove exactly the information which we consider non-local, see Remark 1.15.
Example 1.42 (Classifying algebroid).
Let
![]() $A\rightarrow X$
be an algebra bundle over a Deligne–Mumford stack
$A\rightarrow X$
be an algebra bundle over a Deligne–Mumford stack
![]() $X$
. Let
$X$
. Let
![]() $A^{\times }$
act on
$A^{\times }$
act on
![]() $A$
from the left by inner automorphisms. Then
$A$
from the left by inner automorphisms. Then
![]() $A^{\times }\backslash A$
is an algebra bundle over the relative classifying stack
$A^{\times }\backslash A$
is an algebra bundle over the relative classifying stack
![]() $Y=B_{X}A^{\times }$
. We have an exact sequence of group schemes over
$Y=B_{X}A^{\times }$
. We have an exact sequence of group schemes over
![]() $Y$
,
$Y$
,
where
![]() $I_{Y/X}=A^{\times }\backslash A^{\times }$
. As
$I_{Y/X}=A^{\times }\backslash A^{\times }$
. As
![]() $I_{X}\rightarrow X$
is unramified,
$I_{X}\rightarrow X$
is unramified,
![]() $I_{Y/X}\rightarrow I_{Y}$
is an open embedding, and so
$I_{Y/X}\rightarrow I_{Y}$
is an open embedding, and so
![]() $(Y,A^{\times }\backslash A)$
is an algebroid. If
$(Y,A^{\times }\backslash A)$
is an algebroid. If
![]() $X$
is a space,
$X$
is a space,
![]() $(Y,A^{\times }\backslash A)$
is a strict algebroid.
$(Y,A^{\times }\backslash A)$
is a strict algebroid.
Remark 1.43 (Algebroids which are trivial gerbes are classifying algebroids).
Let
![]() $(X,A)$
be an algebroid such that
$(X,A)$
be an algebroid such that
![]() $A$
is an algebra bundle over
$A$
is an algebra bundle over
![]() $X$
, and therefore
$X$
, and therefore
![]() $X$
is a connected gerbe over the Deligne–Mumford stack
$X$
is a connected gerbe over the Deligne–Mumford stack
![]() $S$
, with
$S$
, with
![]() $A^{\times }=I_{X/S}$
. Suppose the gerbe
$A^{\times }=I_{X/S}$
. Suppose the gerbe
![]() $X\rightarrow S$
admits a section
$X\rightarrow S$
admits a section
![]() $x:S\rightarrow X$
. Via
$x:S\rightarrow X$
. Via
![]() $x$
, we pull back
$x$
, we pull back
![]() $A$
to a bundle of algebras
$A$
to a bundle of algebras
![]() $C$
over
$C$
over
![]() $S$
. We claim that
$S$
. We claim that
![]() $(X,A)$
is canonically isomorphic to
$(X,A)$
is canonically isomorphic to
![]() $(BC^{\times },C^{\times }\backslash C)$
.
$(BC^{\times },C^{\times }\backslash C)$
.
In fact, because
![]() $X$
is a gerbe over
$X$
is a gerbe over
![]() $S$
, the section
$S$
, the section
![]() $x:S\rightarrow X$
is a universal principal
$x:S\rightarrow X$
is a universal principal
![]() $x^{\ast }I_{X/S}$
-bundle. The pullback diagram
$x^{\ast }I_{X/S}$
-bundle. The pullback diagram

shows that
![]() $C$
is an
$C$
is an
![]() $x^{\ast }I_{X/S}$
-bundle over
$x^{\ast }I_{X/S}$
-bundle over
![]() $A$
. Hence,
$A$
. Hence,
![]() $A=C/x^{\ast }I_{X/S}$
. Via the isomorphism
$A=C/x^{\ast }I_{X/S}$
. Via the isomorphism
![]() $\unicode[STIX]{x1D704}:C^{\times }\rightarrow x^{\ast }I_{X/S}$
, the action of
$\unicode[STIX]{x1D704}:C^{\times }\rightarrow x^{\ast }I_{X/S}$
, the action of
![]() $x^{\ast }I_{X/S}$
on
$x^{\ast }I_{X/S}$
on
![]() $C$
is identified with the action by left inner automorphisms. This follows from the algebroid property of
$C$
is identified with the action by left inner automorphisms. This follows from the algebroid property of
![]() $(X,A)$
and proves the claim.
$(X,A)$
and proves the claim.
Remark 1.44. If
![]() $X\rightarrow \operatorname{Spec}R$
is a gerbe, any strict algebroid over
$X\rightarrow \operatorname{Spec}R$
is a gerbe, any strict algebroid over
![]() $X$
can be promoted to a linear algebraic stack whose underlying algebraic stack is
$X$
can be promoted to a linear algebraic stack whose underlying algebraic stack is
![]() $X$
.
$X$
.
More generally, there exists a notion of relative linear algebraic stack, where the base
![]() $R$
is replaced by an arbitrary scheme (or algebraic space). Then every strict algebroid
$R$
is replaced by an arbitrary scheme (or algebraic space). Then every strict algebroid
![]() $(X,A)$
where
$(X,A)$
where
![]() $X$
is a gerbe over a space
$X$
is a gerbe over a space
![]() $S$
becomes naturally a linear algebraic stack over
$S$
becomes naturally a linear algebraic stack over
![]() $S$
. These types of linear algebraic stacks occur naturally in the theory of deformation quantization, where they were introduced by Kontsevich under the name of ‘stack of algebroids’, see [Reference KontsevichKon01]. In [Reference KontsevichKon01], one can also find a description of these stacks of algebroids in terms of cocycles (compare also [Reference D’Agnolo and PoleselloDP05]).
$S$
. These types of linear algebraic stacks occur naturally in the theory of deformation quantization, where they were introduced by Kontsevich under the name of ‘stack of algebroids’, see [Reference KontsevichKon01]. In [Reference KontsevichKon01], one can also find a description of these stacks of algebroids in terms of cocycles (compare also [Reference D’Agnolo and PoleselloDP05]).
Thus, our notion of algebroid is a natural generalization of Kontsevich’s notion of a stack of algebroids. This justifies our terminology.
Loosely speaking, algebroids are stacks which are linear over their coarse Deligne–Mumford stack.
Example 1.45 (Schemes as algebroids).
Every Deligne–Mumford stack
![]() $Z$
is an algebroid via the definition
$Z$
is an algebroid via the definition
![]() $A_{Z}=0_{Z}$
. There is no natural way to enhance the algebroid
$A_{Z}=0_{Z}$
. There is no natural way to enhance the algebroid
![]() $(Z,0_{Z})$
to a linear algebraic stack, unless
$(Z,0_{Z})$
to a linear algebraic stack, unless
![]() $Z=\operatorname{Spec}R$
is the final scheme. This exhibits one way in which algebroids are more flexible than linear algebraic stacks.
$Z=\operatorname{Spec}R$
is the final scheme. This exhibits one way in which algebroids are more flexible than linear algebraic stacks.
Example 1.46 (Algebroids over quotient stacks).
Let
![]() $X=G\backslash Y$
be a quotient stack. A finite type algebra
$X=G\backslash Y$
be a quotient stack. A finite type algebra
![]() $A$
over
$A$
over
![]() $X$
is given by a finite type algebra
$X$
is given by a finite type algebra
![]() $B$
over
$B$
over
![]() $Y$
, together with a lift of the
$Y$
, together with a lift of the
![]() $G$
-action on
$G$
-action on
![]() $X$
to an action on
$X$
to an action on
![]() $B$
by algebra automorphisms. The inertia stack of
$B$
by algebra automorphisms. The inertia stack of
![]() $X$
is naturally identified with
$X$
is naturally identified with
![]() $G\backslash \!\operatorname{Stab}_{G}Y$
. Thus,
$G\backslash \!\operatorname{Stab}_{G}Y$
. Thus,
![]() $(X,A)$
becomes an algebroid if we specify a
$(X,A)$
becomes an algebroid if we specify a
![]() $G$
-equivariant open embedding of
$G$
-equivariant open embedding of
![]() $Y$
-group schemes
$Y$
-group schemes
![]() $\unicode[STIX]{x1D704}:B^{\times }\rightarrow \operatorname{Stab}_{G}Y$
. If
$\unicode[STIX]{x1D704}:B^{\times }\rightarrow \operatorname{Stab}_{G}Y$
. If
![]() $B$
is not an algebra bundle, we also need to require that
$B$
is not an algebra bundle, we also need to require that
![]() $^{u}b=\unicode[STIX]{x1D704}(u)\cdot b$
, for all
$^{u}b=\unicode[STIX]{x1D704}(u)\cdot b$
, for all
![]() $u\in B^{\times }$
,
$u\in B^{\times }$
,
![]() $b\in B$
.
$b\in B$
.
Morphisms of algebroids
Definition 1.47. We call a morphism of algebraic stacks
![]() $f:X\rightarrow Y$
inert, if the diagram of stacks
$f:X\rightarrow Y$
inert, if the diagram of stacks

is cartesian. If
![]() $I_{X}\rightarrow I_{Y}|_{X}$
is an isomorphism, we call
$I_{X}\rightarrow I_{Y}|_{X}$
is an isomorphism, we call
![]() $f$
strictly inert.
$f$
strictly inert.
The connected component
![]() $I_{Y}^{\circ }$
is not necessarily an algebraic stack, but if it is, then so is
$I_{Y}^{\circ }$
is not necessarily an algebraic stack, but if it is, then so is
![]() $I_{X}^{\circ }$
, if
$I_{X}^{\circ }$
, if
![]() $X\rightarrow Y$
is inert. We will only apply this concept when
$X\rightarrow Y$
is inert. We will only apply this concept when
![]() $Y$
is an algebroid, so that
$Y$
is an algebroid, so that
![]() $I_{Y}^{\circ }$
is representable over
$I_{Y}^{\circ }$
is representable over
![]() $Y$
.
$Y$
.
The basic facts about inert morphisms are as follows.
(i) Every inert morphism of algebraic stacks is Deligne–Mumford representable, because its relative inertia group scheme is unramified.
(ii) Every base change of an inert morphism of algebraic stacks is inert.
(iii) Every monomorphism of algebraic stacks (in particular, every locally closed immersion and every stratification) is (strictly) inert.
(iv) Being inert is local in the étale topology of the target.
(v) Every morphism of Deligne–Mumford stacks is inert.
Base changes of morphisms of Deligne–Mumford stacks are, in fact, the only inert morphisms, at least up to stratifications.
Proposition 1.48. Suppose
![]() $X\rightarrow Y$
is an inert morphism of algebraic stacks, and suppose
$X\rightarrow Y$
is an inert morphism of algebraic stacks, and suppose
![]() $I_{Y}^{\circ }$
(and hence also
$I_{Y}^{\circ }$
(and hence also
![]() $I_{X}^{\circ }$
) is smooth and representable over
$I_{X}^{\circ }$
) is smooth and representable over
![]() $X$
, so that we have coarse Deligne–Mumford stacks
$X$
, so that we have coarse Deligne–Mumford stacks
![]() $\overline{X}$
,
$\overline{X}$
,
![]() $\overline{Y}$
and an induced morphism
$\overline{Y}$
and an induced morphism
![]() $\overline{X}\rightarrow \overline{Y}$
. Then the diagram
$\overline{X}\rightarrow \overline{Y}$
. Then the diagram

is cartesian.
Proof. To prove that the morphism of gerbes
![]() $X\rightarrow Y|_{\overline{X}}$
over
$X\rightarrow Y|_{\overline{X}}$
over
![]() $\overline{X}$
is an isomorphism, we may pass to an étale cover
$\overline{X}$
is an isomorphism, we may pass to an étale cover
![]() $\overline{X}^{\prime }$
of
$\overline{X}^{\prime }$
of
![]() $X$
and assume that the gerbe
$X$
and assume that the gerbe
![]() $X$
is trivial. Then
$X$
is trivial. Then
![]() $X=B_{\overline{X}}G$
, where
$X=B_{\overline{X}}G$
, where
![]() $G$
is the pullback of
$G$
is the pullback of
![]() $I_{X}^{\circ }$
to
$I_{X}^{\circ }$
to
![]() $\overline{X}$
via a trivializing section. Moreover,
$\overline{X}$
via a trivializing section. Moreover,
![]() $Y|_{\overline{X}}=B_{\overline{X}}H$
, where
$Y|_{\overline{X}}=B_{\overline{X}}H$
, where
![]() $H$
is the pullback of
$H$
is the pullback of
![]() $I_{Y}^{\circ }|_{X}$
to
$I_{Y}^{\circ }|_{X}$
to
![]() $\overline{X}$
via the same trivializing section. Since
$\overline{X}$
via the same trivializing section. Since
![]() $I_{X}^{\circ }\rightarrow I_{Y}^{\circ }|_{X}$
is an isomorphism, so is
$I_{X}^{\circ }\rightarrow I_{Y}^{\circ }|_{X}$
is an isomorphism, so is
![]() $G\rightarrow H$
, and hence
$G\rightarrow H$
, and hence
![]() $X\rightarrow Y|_{\overline{X}}$
.◻
$X\rightarrow Y|_{\overline{X}}$
.◻
Definition 1.49. A morphism of algebroids
![]() $X\rightarrow Y$
is a pair
$X\rightarrow Y$
is a pair
![]() $(f,\unicode[STIX]{x1D711})$
where
$(f,\unicode[STIX]{x1D711})$
where
![]() $f:X\rightarrow Y$
is a morphism of algebraic stacks and
$f:X\rightarrow Y$
is a morphism of algebraic stacks and
![]() $\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}$
is a morphism of algebras over
$\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}$
is a morphism of algebras over
![]() $f$
such that the diagram
$f$
such that the diagram
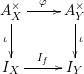
commutes.
The morphism
![]() $(f,\unicode[STIX]{x1D711})$
is a representable morphism of algebroids if
$(f,\unicode[STIX]{x1D711})$
is a representable morphism of algebroids if
![]() $\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}|_{X}$
is a monomorphism of sheaves of algebras over
$\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}|_{X}$
is a monomorphism of sheaves of algebras over
![]() $X$
. (This implies that
$X$
. (This implies that
![]() $f$
is Deligne–Mumford representable.)
$f$
is Deligne–Mumford representable.)
The morphism
![]() $(f,\unicode[STIX]{x1D711})$
is inert if
$(f,\unicode[STIX]{x1D711})$
is inert if
![]() $\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}|_{X}$
is an isomorphism of finite type algebras. (This implies that
$\unicode[STIX]{x1D711}:A_{X}\rightarrow A_{Y}|_{X}$
is an isomorphism of finite type algebras. (This implies that
![]() $f$
is inert.)
$f$
is inert.)
There is a natural notion of 2-morphism of algebroid, which makes algebroids into a 2-category.
Remark 1.50 (Inert morphisms in the case of algebra bundles).
Suppose
![]() $(X,A_{X})\rightarrow (Y,A_{Y})$
is a morphism of algebroids, where
$(X,A_{X})\rightarrow (Y,A_{Y})$
is a morphism of algebroids, where
![]() $A_{X}$
and
$A_{X}$
and
![]() $A_{Y}$
are algebra bundles. If
$A_{Y}$
are algebra bundles. If
![]() $X\rightarrow Y$
is an inert morphism of algebraic stacks, then we automatically have
$X\rightarrow Y$
is an inert morphism of algebraic stacks, then we automatically have
![]() $A_{X}^{\times }=A_{Y}^{\times }|_{X}$
and hence
$A_{X}^{\times }=A_{Y}^{\times }|_{X}$
and hence
![]() $A_{X}=A_{Y}|_{X}$
, and so
$A_{X}=A_{Y}|_{X}$
, and so
![]() $(X,A_{X})\rightarrow (Y,A_{Y})$
is an inert morphism of algebroids.
$(X,A_{X})\rightarrow (Y,A_{Y})$
is an inert morphism of algebroids.
Remark 1.51 (Strict algebroids and representable morphisms).
Suppose
![]() $(X,A)$
is a strict algebroid and
$(X,A)$
is a strict algebroid and
![]() $f:Y\rightarrow X$
a representable morphism of algebraic stacks. If
$f:Y\rightarrow X$
a representable morphism of algebraic stacks. If
![]() $B\subset A|_{Y}$
is a finite type subalgebra such that
$B\subset A|_{Y}$
is a finite type subalgebra such that
![]() $\unicode[STIX]{x1D704}(B^{\times })=I_{Y}\cap \unicode[STIX]{x1D704}(A^{\times }|_{Y})$
inside
$\unicode[STIX]{x1D704}(B^{\times })=I_{Y}\cap \unicode[STIX]{x1D704}(A^{\times }|_{Y})$
inside
![]() $I_{X}|_{Y}$
, then
$I_{X}|_{Y}$
, then
![]() $(Y,B)$
is a strict algebroid with a representable morphism
$(Y,B)$
is a strict algebroid with a representable morphism
![]() $(Y,B)\rightarrow (X,A)$
. (The algebroid condition for
$(Y,B)\rightarrow (X,A)$
. (The algebroid condition for
![]() $(Y,B)$
is automatic.)
$(Y,B)$
is automatic.)
Every strict algebroid over
![]() $f:Y\rightarrow X$
and
$f:Y\rightarrow X$
and
![]() $(X,A)$
comes about in this way.
$(X,A)$
comes about in this way.
Remark 1.52 (Pullbacks).
Suppose
![]() $(X,A_{X})$
is an algebroid and
$(X,A_{X})$
is an algebroid and
![]() $Y\rightarrow X$
an inert morphism of algebraic stacks. In this case,
$Y\rightarrow X$
an inert morphism of algebraic stacks. In this case,
![]() $Y$
admits a unique algebroid
$Y$
admits a unique algebroid
![]() $A_{Y}$
endowed with an inert morphism of algebroids
$A_{Y}$
endowed with an inert morphism of algebroids
![]() $(Y,A_{Y})\rightarrow (X,A_{X})$
. In fact,
$(Y,A_{Y})\rightarrow (X,A_{X})$
. In fact,
![]() $A_{Y}=A_{X}|_{Y}$
.
$A_{Y}=A_{X}|_{Y}$
.
If
![]() $(X,A_{X})$
is a strict algebroid, then the morphism
$(X,A_{X})$
is a strict algebroid, then the morphism
![]() $Y\rightarrow X$
is necessarily strictly inert, and
$Y\rightarrow X$
is necessarily strictly inert, and
![]() $(Y,A_{Y})$
is necessarily a strict algebroid. We call
$(Y,A_{Y})$
is necessarily a strict algebroid. We call
![]() $(Y,A_{Y})\rightarrow (X,A_{X})$
a strictly inert morphism of strict algebroids.
$(Y,A_{Y})\rightarrow (X,A_{X})$
a strictly inert morphism of strict algebroids.
Definition 1.53. We call a morphism of algebroids
![]() $(X,A_{X})\rightarrow (Y,A_{Y})$
$(X,A_{X})\rightarrow (Y,A_{Y})$
(i) a vector bundle,
(ii) a principal homogeneous
 $G$
-bundle, for an algebraic group
$G$
-bundle, for an algebraic group
 $G$
,
$G$
,(iii) a fibre bundle with group
 $G$
and fibre
$G$
and fibre
 $F$
,
$F$
,(iv) a locally closed immersion,
(v) a stratification,
if it is inert and the underlying morphism of algebraic stacks
![]() $X\rightarrow Y$
has the indicated property.
$X\rightarrow Y$
has the indicated property.
Remark 1.54 (Fibred products).
Fibred products of algebroids exist and commute with fibred products of underlying stacks and underlying algebras. Fibred products of strict algebroids are strict algebroids. The algebroid underlying a fibred product of linear algebraic stacks is equal to the fibred product of the underlying algebroids.
Proposition 1.55. Suppose
![]() $(X,A)\rightarrow (Y,B)$
is a morphism of algebroids where
$(X,A)\rightarrow (Y,B)$
is a morphism of algebroids where
![]() $X\rightarrow Y$
is a stratification of algebraic stacks. Then there exists a stratification of algebroids
$X\rightarrow Y$
is a stratification of algebraic stacks. Then there exists a stratification of algebroids
![]() $(X^{\prime },A^{\prime })\rightarrow (X,A)$
such that the composition
$(X^{\prime },A^{\prime })\rightarrow (X,A)$
such that the composition
![]() $(X^{\prime },A^{\prime })\rightarrow (Y,B)$
is also a stratification of algebroids.
$(X^{\prime },A^{\prime })\rightarrow (Y,B)$
is also a stratification of algebroids.
If
![]() $(Y,B)$
is strict, then
$(Y,B)$
is strict, then
![]() $(X^{\prime },A^{\prime })\rightarrow (X,A)$
and
$(X^{\prime },A^{\prime })\rightarrow (X,A)$
and
![]() $(X^{\prime },A^{\prime })\rightarrow (Y,B)$
are stratifications of strict algebroids.
$(X^{\prime },A^{\prime })\rightarrow (Y,B)$
are stratifications of strict algebroids.
Proof. Passing to the rank stratifications of
![]() $A$
and
$A$
and
![]() $B$
, we obtain a commutative diagram of algebroids.
$B$
, we obtain a commutative diagram of algebroids.

The upper horizontal morphism is an inert morphism of algebroids, because
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $B^{\prime }$
are algebra bundles, by Remark 1.50. The claim follows.◻
$B^{\prime }$
are algebra bundles, by Remark 1.50. The claim follows.◻
Algebroid inertia
Remark 1.56 (Inertia).
Let
![]() $(X,A)$
be an algebroid. Then
$(X,A)$
be an algebroid. Then
![]() $(I_{X},I_{A})$
is another algebroid, which we call the algebroid inertia of
$(I_{X},I_{A})$
is another algebroid, which we call the algebroid inertia of
![]() $(X,A)$
. In fact,
$(X,A)$
. In fact,
![]() $I_{A}=(A|_{I_{X}})^{\text{fix}}$
, the subalgebra of
$I_{A}=(A|_{I_{X}})^{\text{fix}}$
, the subalgebra of
![]() $A|_{I_{X}}$
of elements invariant under the tautological automorphism induced by the inertia action of
$A|_{I_{X}}$
of elements invariant under the tautological automorphism induced by the inertia action of
![]() $I_{X}$
on
$I_{X}$
on
![]() $A$
. The subgroup of units is
$A$
. The subgroup of units is
![]() $(A^{\times }|_{I_{X}})^{\text{fix}}$
, and we have the following cartesian diagram.
$(A^{\times }|_{I_{X}})^{\text{fix}}$
, and we have the following cartesian diagram.

If
![]() $(X,A)$
is a strict algebroid, then so is
$(X,A)$
is a strict algebroid, then so is
![]() $(I_{X},I_{A})$
.
$(I_{X},I_{A})$
.
Remark 1.57 (Induced algebroid structure on the algebra).
Let
![]() $(X,A)$
be an algebroid. Let
$(X,A)$
be an algebroid. Let
![]() $(A|_{A})^{\text{fix}}$
be the subalgebra of the pullback
$(A|_{A})^{\text{fix}}$
be the subalgebra of the pullback
![]() $A|_{A}$
of elements commuting with the tautological section of
$A|_{A}$
of elements commuting with the tautological section of
![]() $A|_{A}$
. (This is equal to the space of commuting pairs in
$A|_{A}$
. (This is equal to the space of commuting pairs in
![]() $A\times _{X}A$
). The subgroup of units is
$A\times _{X}A$
). The subgroup of units is
![]() $(A^{\times }|_{A})^{\text{fix}}$
, and we have the following cartesian diagram.
$(A^{\times }|_{A})^{\text{fix}}$
, and we have the following cartesian diagram.

This proves that
![]() $(A,(A|_{A})^{\text{fix}})$
is an algebroid over
$(A,(A|_{A})^{\text{fix}})$
is an algebroid over
![]() $A$
.
$A$
.
In fact, we have a commutative diagram of algebroids.

If
![]() $(X,A)$
is a strict algebroid, this is a diagram of strict algebroids.
$(X,A)$
is a strict algebroid, this is a diagram of strict algebroids.
Remark 1.58 (Semi-simple algebroid inertia).
There is also a semi-simple version of the algebroid inertia. To define it, let
![]() $(X,A)$
be an algebroid, and consider the following diagram of algebroids.
$(X,A)$
be an algebroid, and consider the following diagram of algebroids.

The square on the right was constructed in Remark 1.57. The morphism
![]() $A^{\text{ss}}\rightarrow A$
is the composition of a stratification and an open immersion (see Proposition 1.34); in particular, it is inert. Hence, we get an induced algebroid structure on
$A^{\text{ss}}\rightarrow A$
is the composition of a stratification and an open immersion (see Proposition 1.34); in particular, it is inert. Hence, we get an induced algebroid structure on
![]() $A^{\text{ss}}$
. Requiring the square on the left to be a cartesian diagram of algebroids defines the algebraic stack
$A^{\text{ss}}$
. Requiring the square on the left to be a cartesian diagram of algebroids defines the algebraic stack
![]() $A^{\times ,\text{ss}}$
and the algebroid structure over it.
$A^{\times ,\text{ss}}$
and the algebroid structure over it.
If
![]() $(X,A)$
is a strict algebroid, all objects in Diagram (9) are strict, and
$(X,A)$
is a strict algebroid, all objects in Diagram (9) are strict, and
![]() $\unicode[STIX]{x1D704}$
is an isomorphism. We are then justified in defining
$\unicode[STIX]{x1D704}$
is an isomorphism. We are then justified in defining
![]() $I_{X}^{\text{ss}}=A^{\times ,\text{ss}}$
and calling it the semi-simple algebroid inertia of
$I_{X}^{\text{ss}}=A^{\times ,\text{ss}}$
and calling it the semi-simple algebroid inertia of
![]() $X$
. In the general case we define
$X$
. In the general case we define
![]() $I_{X}^{\circ ,\text{ss}}=A^{\times ,\text{ss}}$
and also call it the semi-simple algebroid inertia, by a slight abuse of language.
$I_{X}^{\circ ,\text{ss}}=A^{\times ,\text{ss}}$
and also call it the semi-simple algebroid inertia, by a slight abuse of language.
Idempotents and algebroids
Lemma 1.59. Let
![]() $a\in A^{\times ,\text{ss}}$
be a semi-simple invertible global section of an algebra bundle
$a\in A^{\times ,\text{ss}}$
be a semi-simple invertible global section of an algebra bundle
![]() $A\rightarrow X$
. Let
$A\rightarrow X$
. Let
![]() $\widetilde{A}^{\times ,\text{ss}}=A^{\times ,\text{ss}}/\mathbb{G}_{m}$
be the quotient of
$\widetilde{A}^{\times ,\text{ss}}=A^{\times ,\text{ss}}/\mathbb{G}_{m}$
be the quotient of
![]() $A^{\times ,\text{ss}}$
by the subgroup of scalars. Consider the action of the group
$A^{\times ,\text{ss}}$
by the subgroup of scalars. Consider the action of the group
![]() $A^{\times }$
on
$A^{\times }$
on
![]() $A^{\times ,\text{ss}}\rightarrow \widetilde{A}^{\times ,\text{ss}}$
by conjugation. The induced group homomorphism
$A^{\times ,\text{ss}}\rightarrow \widetilde{A}^{\times ,\text{ss}}$
by conjugation. The induced group homomorphism
where
![]() $[a]$
is the class of
$[a]$
is the class of
![]() $a$
in
$a$
in
![]() $\widetilde{A}^{\times ,\text{ss}}$
, is an open immersion.
$\widetilde{A}^{\times ,\text{ss}}$
, is an open immersion.
Proof. Let
![]() $Y_{a}$
be the relative spectrum of
$Y_{a}$
be the relative spectrum of
![]() $\mathscr{O}_{X}[a]$
over
$\mathscr{O}_{X}[a]$
over
![]() $X$
. The epimorphism of commutative algebras
$X$
. The epimorphism of commutative algebras
![]() $\mathscr{O}_{X}[x]\rightarrow \mathscr{O}_{X}[a]$
gives rise to a closed immersion
$\mathscr{O}_{X}[x]\rightarrow \mathscr{O}_{X}[a]$
gives rise to a closed immersion
![]() $\unicode[STIX]{x1D711}:Y_{a}\rightarrow (\mathbb{G}_{m})_{X}$
, because
$\unicode[STIX]{x1D711}:Y_{a}\rightarrow (\mathbb{G}_{m})_{X}$
, because
![]() $a$
is invertible. We get an induced proper morphism
$a$
is invertible. We get an induced proper morphism
As
![]() $Y_{a}\rightarrow X$
is unramified, the diagonal
$Y_{a}\rightarrow X$
is unramified, the diagonal
![]() $Y_{a}\rightarrow Y_{a}\times _{X}Y_{a}$
is an open immersion, so the complement, denoted by
$Y_{a}\rightarrow Y_{a}\times _{X}Y_{a}$
is an open immersion, so the complement, denoted by
![]() $(Y_{a}\times Y_{a})^{\not =}$
, is closed in
$(Y_{a}\times Y_{a})^{\not =}$
, is closed in
![]() $Y_{a}\times Y_{a}$
and hence proper over
$Y_{a}\times Y_{a}$
and hence proper over
![]() $X$
. Hence, the image of
$X$
. Hence, the image of
![]() $(Y_{a}\times Y_{a})^{\not =}$
in
$(Y_{a}\times Y_{a})^{\not =}$
in
![]() $(\mathbb{G}_{m})_{X}$
, denoted by
$(\mathbb{G}_{m})_{X}$
, denoted by
![]() $Z$
, is closed. The complement of
$Z$
, is closed. The complement of
![]() $Z$
in
$Z$
in
![]() $(\mathbb{G}_{m})_{X}$
is hence an open neighbourhood
$(\mathbb{G}_{m})_{X}$
is hence an open neighbourhood
![]() $U$
of the identity section.
$U$
of the identity section.
We have the following cartesian diagram.

The lower square is cartesian by the definition of
![]() $\operatorname{Stab}_{A^{\times }}[a]$
. The fact that the upper square is cartesian follows from the fact that the image of
$\operatorname{Stab}_{A^{\times }}[a]$
. The fact that the upper square is cartesian follows from the fact that the image of
![]() $\operatorname{Stab}_{A^{\times }}[a]$
in
$\operatorname{Stab}_{A^{\times }}[a]$
in
![]() $(\mathbb{G}_{m})_{X}$
is contained in the image of (10). The latter claim follows from the fact that if
$(\mathbb{G}_{m})_{X}$
is contained in the image of (10). The latter claim follows from the fact that if
![]() $^{b}a=\unicode[STIX]{x1D706}a$
, for a scalar
$^{b}a=\unicode[STIX]{x1D706}a$
, for a scalar
![]() $\unicode[STIX]{x1D706}\in (\mathbb{G}_{m})_{X}$
, then
$\unicode[STIX]{x1D706}\in (\mathbb{G}_{m})_{X}$
, then
![]() $\unicode[STIX]{x1D706}$
is necessarily a quotient of eigenvalues of
$\unicode[STIX]{x1D706}$
is necessarily a quotient of eigenvalues of
![]() $a$
. (Use Remark 1.24 to assume that
$a$
. (Use Remark 1.24 to assume that
![]() $a$
is a matrix. Then
$a$
is a matrix. Then
![]() $^{b}a=\unicode[STIX]{x1D706}a$
implies that
$^{b}a=\unicode[STIX]{x1D706}a$
implies that
![]() $a$
and
$a$
and
![]() $^{b}a$
are simultaneously diagonalizable. Once we have diagonalized,
$^{b}a$
are simultaneously diagonalizable. Once we have diagonalized,
![]() $a$
and
$a$
and
![]() $^{b}a$
are the same up to permutation of the diagonal entries.)◻
$^{b}a$
are the same up to permutation of the diagonal entries.)◻
Remark 1.60. Let
![]() $(X,A)$
be an algebroid, and let
$(X,A)$
be an algebroid, and let
![]() $Y=E_{k}(A)$
be the stack of complete labelled sets of
$Y=E_{k}(A)$
be the stack of complete labelled sets of
![]() $k$
orthogonal idempotents in
$k$
orthogonal idempotents in
![]() $A$
. Let us write
$A$
. Let us write
![]() $B=(A|_{Y})^{e_{1},\ldots ,e_{k}}$
for the subalgebra of
$B=(A|_{Y})^{e_{1},\ldots ,e_{k}}$
for the subalgebra of
![]() $A|_{Y}$
consisting of elements commuting with each of the
$A|_{Y}$
consisting of elements commuting with each of the
![]() $k$
tautological idempotents in
$k$
tautological idempotents in
![]() $A|_{Y}$
. The homomorphism
$A|_{Y}$
. The homomorphism
![]() $\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
restricts to a homomorphism
$\unicode[STIX]{x1D704}:A^{\times }\rightarrow I_{X}$
restricts to a homomorphism
![]() $B^{\times }\rightarrow I_{Y}$
and defines an algebroid structure over
$B^{\times }\rightarrow I_{Y}$
and defines an algebroid structure over
![]() $Y$
. The algebra
$Y$
. The algebra
![]() $B$
is endowed with a canonical complete set of orthogonal central idempotents and hence decomposes as a product
$B$
is endowed with a canonical complete set of orthogonal central idempotents and hence decomposes as a product
![]() $B=B_{1}\times \cdots \times B_{k}$
.
$B=B_{1}\times \cdots \times B_{k}$
.
Let
![]() $(X,A)$
be an algebroid, where
$(X,A)$
be an algebroid, where
![]() $A$
is an algebra bundle, and let
$A$
is an algebra bundle, and let
![]() $e_{1},\ldots ,e_{k}$
be orthogonal central idempotents in
$e_{1},\ldots ,e_{k}$
be orthogonal central idempotents in
![]() $A$
, decomposing
$A$
, decomposing
![]() $A$
into a product of algebra bundles
$A$
into a product of algebra bundles
![]() $A=A_{1}\times \cdots \times A_{k}$
. We get an induced decomposition
$A=A_{1}\times \cdots \times A_{k}$
. We get an induced decomposition
and the algebroid structure on
![]() $A^{\times ,\text{ss}}$
is the fibred product over
$A^{\times ,\text{ss}}$
is the fibred product over
![]() $X$
of the algebroid structures on the
$X$
of the algebroid structures on the
![]() $A_{i}^{\times ,\text{ss}}$
,
$A_{i}^{\times ,\text{ss}}$
,
![]() $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
.
We obtain an embedding of algebras
![]() $\unicode[STIX]{x1D6FC}:\mathbb{A}_{X}^{k}\rightarrow A$
mapping
$\unicode[STIX]{x1D6FC}:\mathbb{A}_{X}^{k}\rightarrow A$
mapping
![]() $(a_{1},\ldots ,a_{k})$
to
$(a_{1},\ldots ,a_{k})$
to
![]() $\sum a_{i}e_{i}\in A$
. Via
$\sum a_{i}e_{i}\in A$
. Via
![]() $\unicode[STIX]{x1D6FC}$
, the torus
$\unicode[STIX]{x1D6FC}$
, the torus
![]() $\mathbb{G}_{m}^{k}$
acts on
$\mathbb{G}_{m}^{k}$
acts on
![]() $A$
by left multiplication. The action of
$A$
by left multiplication. The action of
![]() $\mathbb{G}_{m}^{k}$
on
$\mathbb{G}_{m}^{k}$
on
![]() $A$
preserves the semi-simple units, and the restricted action of
$A$
preserves the semi-simple units, and the restricted action of
![]() $\mathbb{G}_{m}^{k}$
on
$\mathbb{G}_{m}^{k}$
on
![]() $A^{\times ,\text{ss}}$
is fibrewise free, so the quotient
$A^{\times ,\text{ss}}$
is fibrewise free, so the quotient
is representable over
![]() $X$
.
$X$
.
Proposition 1.61. We claim that
![]() $\widetilde{A}^{\times ,\text{ss}}$
has a canonical algebroid structure, and we get an induced commutative diagram
$\widetilde{A}^{\times ,\text{ss}}$
has a canonical algebroid structure, and we get an induced commutative diagram

of algebroids where the horizontal map is inert, and hence a principal
![]() $\mathbb{G}_{m}^{k}$
-bundle of algebroids.
$\mathbb{G}_{m}^{k}$
-bundle of algebroids.
Proof. Because inert morphisms of algebroids are stable under composition and pullback, this claim reduces to the case
![]() $k=1$
and
$k=1$
and
![]() $e_{1}=1$
, which we will now consider.
$e_{1}=1$
, which we will now consider.
Let us denote the tautological section of
![]() $A^{\times }$
over
$A^{\times }$
over
![]() $A^{\times ,\text{ss}}$
by
$A^{\times ,\text{ss}}$
by
![]() $a$
. Then the algebra over
$a$
. Then the algebra over
![]() $A^{\times ,\text{ss}}$
is given by the centralizer algebra
$A^{\times ,\text{ss}}$
is given by the centralizer algebra
![]() $(A|_{A^{\times ,\text{ss}}})^{a}$
. This algebra descends to the quotient
$(A|_{A^{\times ,\text{ss}}})^{a}$
. This algebra descends to the quotient
![]() $\widetilde{A}^{\times ,\text{ss}}$
, because the centralizer of an algebra element does not depend on its equivalence class. Let us denote this descended algebra by
$\widetilde{A}^{\times ,\text{ss}}$
, because the centralizer of an algebra element does not depend on its equivalence class. Let us denote this descended algebra by
![]() $(A|_{\widetilde{A}^{\times ,\text{ss}}})^{[a]}$
. The units in this algebra are identified with
$(A|_{\widetilde{A}^{\times ,\text{ss}}})^{[a]}$
. The units in this algebra are identified with
which is an open subgroup of
by Lemma 1.59. We also have a cartesian diagram

because the inertia stack
![]() $I_{\widetilde{A}^{\times ,\text{ss}}}$
can be identified as
$I_{\widetilde{A}^{\times ,\text{ss}}}$
can be identified as
This proves that
![]() $\operatorname{Stab}_{(A^{\times }|_{\widetilde{A}^{\times ,\text{ss}}})}[a]$
is an open subgroup of
$\operatorname{Stab}_{(A^{\times }|_{\widetilde{A}^{\times ,\text{ss}}})}[a]$
is an open subgroup of
![]() $I_{\widetilde{A}^{\times ,\text{ss}}}$
. Composing our two open immersions, we obtain an open immersion of groups over
$I_{\widetilde{A}^{\times ,\text{ss}}}$
. Composing our two open immersions, we obtain an open immersion of groups over
![]() $\widetilde{A}^{\times ,\text{ss}}$
from
$\widetilde{A}^{\times ,\text{ss}}$
from
![]() $(A^{\times }|_{\widetilde{A}^{\times ,\text{ss}}})^{[a]}$
to
$(A^{\times }|_{\widetilde{A}^{\times ,\text{ss}}})^{[a]}$
to
![]() $I_{\widetilde{A}^{\times ,\text{ss}}}$
, endowing
$I_{\widetilde{A}^{\times ,\text{ss}}}$
, endowing
![]() $\widetilde{A}^{\times ,\text{ss}}$
with the structure of an algebroid, as required.
$\widetilde{A}^{\times ,\text{ss}}$
with the structure of an algebroid, as required.
We get an induced morphism of algebroids
![]() $A^{\times ,\text{ss}}\rightarrow \widetilde{A}^{\times ,\text{ss}}$
, which is inert, by construction.◻
$A^{\times ,\text{ss}}\rightarrow \widetilde{A}^{\times ,\text{ss}}$
, which is inert, by construction.◻
Remark 1.62. Even if
![]() $(X,A)$
is strict,
$(X,A)$
is strict,
![]() $\widetilde{A}^{\times ,\text{ss}}$
is not necessarily strict. It is this construction, in fact, which makes it impossible for us to restrict attention to strict algebroids.
$\widetilde{A}^{\times ,\text{ss}}$
is not necessarily strict. It is this construction, in fact, which makes it impossible for us to restrict attention to strict algebroids.
Remark 1.63. Let
![]() $(\mathfrak{M},\mathfrak{A})$
be the algebroid underlying a linear algebraic stack. Suppose that
$(\mathfrak{M},\mathfrak{A})$
be the algebroid underlying a linear algebraic stack. Suppose that
![]() $\mathfrak{M}$
admits direct sums. Let
$\mathfrak{M}$
admits direct sums. Let
![]() $\mathfrak{M}_{\ast }$
be the complement of the zero object in
$\mathfrak{M}_{\ast }$
be the complement of the zero object in
![]() $\mathfrak{M}$
. We obtain a canonical morphism of algebroids
$\mathfrak{M}$
. We obtain a canonical morphism of algebroids
 $$\begin{eqnarray}\displaystyle \underbrace{\mathfrak{M}_{\ast }\times \cdots \times \mathfrak{M}_{\ast }}_{n\text{ times}} & \longrightarrow & \displaystyle E_{n}(\mathfrak{A})\nonumber\\ \displaystyle (x_{1},\ldots ,x_{n}) & \longmapsto & \displaystyle (x_{1}\oplus \cdots \oplus x_{n};\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{n}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underbrace{\mathfrak{M}_{\ast }\times \cdots \times \mathfrak{M}_{\ast }}_{n\text{ times}} & \longrightarrow & \displaystyle E_{n}(\mathfrak{A})\nonumber\\ \displaystyle (x_{1},\ldots ,x_{n}) & \longmapsto & \displaystyle (x_{1}\oplus \cdots \oplus x_{n};\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{n}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{n}$
are the projectors corresponding to the factors
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{n}$
are the projectors corresponding to the factors
![]() $x_{1},\ldots ,x_{n}$
of
$x_{1},\ldots ,x_{n}$
of
![]() $x_{1}\oplus \cdots \oplus x_{n}$
. Over every
$x_{1}\oplus \cdots \oplus x_{n}$
. Over every
![]() $R$
-scheme
$R$
-scheme
![]() $S$
, this morphism is fully faithful. The underlying morphism of algebraic stacks (11) is a monomorphism.
$S$
, this morphism is fully faithful. The underlying morphism of algebraic stacks (11) is a monomorphism.
If we require all fibres
![]() $\mathfrak{M}(S)$
to be Karoubian, i.e., we require all idempotents to admit the corresponding direct summands, (11) is an isomorphism of algebroids.
$\mathfrak{M}(S)$
to be Karoubian, i.e., we require all idempotents to admit the corresponding direct summands, (11) is an isomorphism of algebroids.
We say a linear algebraic stack
![]() $\mathfrak{M}$
is Karoubian if it admits direct sums and all fibres are Karoubian.
$\mathfrak{M}$
is Karoubian if it admits direct sums and all fibres are Karoubian.
Algebroid representations
Definition 1.64. Let
![]() $X$
be an algebroid. A representation of
$X$
be an algebroid. A representation of
![]() $X$
is a morphism of algebroids
$X$
is a morphism of algebroids
![]() $\unicode[STIX]{x1D70C}:X\rightarrow \mathfrak{Vect}$
to the algebroid underlying the linear stack
$\unicode[STIX]{x1D70C}:X\rightarrow \mathfrak{Vect}$
to the algebroid underlying the linear stack
![]() $\mathfrak{Vect}$
of vector bundles. If
$\mathfrak{Vect}$
of vector bundles. If
![]() $\unicode[STIX]{x1D70C}$
factors through vector bundles of rank
$\unicode[STIX]{x1D70C}$
factors through vector bundles of rank
![]() $n$
, i.e., defines a morphism
$n$
, i.e., defines a morphism
![]() $X\rightarrow B\operatorname{GL}_{n}$
with its natural algebroid structure (see Example 1.41), we say that
$X\rightarrow B\operatorname{GL}_{n}$
with its natural algebroid structure (see Example 1.41), we say that
![]() $\unicode[STIX]{x1D70C}$
has rank
$\unicode[STIX]{x1D70C}$
has rank
![]() $n$
.
$n$
.
If the algebroid morphism
![]() $X\rightarrow B\operatorname{GL}_{n}$
is representable, we say the representation
$X\rightarrow B\operatorname{GL}_{n}$
is representable, we say the representation
![]() $\unicode[STIX]{x1D70C}$
is faithful.
$\unicode[STIX]{x1D70C}$
is faithful.
To give a representation of the algebroid
![]() $(X,A)$
is equivalent to specifying a vector bundle
$(X,A)$
is equivalent to specifying a vector bundle
![]() $V$
over
$V$
over
![]() $X$
together with a morphism of algebras
$X$
together with a morphism of algebras
![]() $A\rightarrow \operatorname{End}(V)$
such that the induced morphism on unit groups
$A\rightarrow \operatorname{End}(V)$
such that the induced morphism on unit groups
![]() $A^{\times }\rightarrow \operatorname{GL}(V)$
makes the diagram
$A^{\times }\rightarrow \operatorname{GL}(V)$
makes the diagram

commute, where
![]() $I_{X}\rightarrow \operatorname{GL}(V)$
is the inertia representation given by the vector bundle
$I_{X}\rightarrow \operatorname{GL}(V)$
is the inertia representation given by the vector bundle
![]() $V/X$
.
$V/X$
.
The representation
![]() $V$
of rank
$V$
of rank
![]() $n$
is faithful if and only if
$n$
is faithful if and only if
![]() $A\rightarrow \operatorname{End}(V)$
is a monomorphism of algebras over
$A\rightarrow \operatorname{End}(V)$
is a monomorphism of algebras over
![]() $X$
. If this is the case, the underlying morphism of stacks
$X$
. If this is the case, the underlying morphism of stacks
![]() $X\rightarrow B\operatorname{GL}_{n}$
is Deligne–Mumford representable, and the
$X\rightarrow B\operatorname{GL}_{n}$
is Deligne–Mumford representable, and the
![]() $\operatorname{GL}_{n}$
-bundle of frames
$\operatorname{GL}_{n}$
-bundle of frames
![]() $Y=\operatorname{Isom̲}(V,\mathscr{O}^{n})$
is represented by a Deligne–Mumford stack.
$Y=\operatorname{Isom̲}(V,\mathscr{O}^{n})$
is represented by a Deligne–Mumford stack.
So, a faithful representation identifies
![]() $X$
as a quotient stack
$X$
as a quotient stack
![]() $X=\operatorname{GL}_{n}\!\backslash Y$
, where
$X=\operatorname{GL}_{n}\!\backslash Y$
, where
![]() $Y$
is a Deligne–Mumford stack. The algebroid structure on
$Y$
is a Deligne–Mumford stack. The algebroid structure on
![]() $X$
is then given by a
$X$
is then given by a
![]() $\operatorname{GL}_{n}$
-invariant subalgebra
$\operatorname{GL}_{n}$
-invariant subalgebra
![]() $B{\hookrightarrow}M_{n\times n}\times Y$
such that the subgroup
$B{\hookrightarrow}M_{n\times n}\times Y$
such that the subgroup
![]() $B^{\times }{\hookrightarrow}\operatorname{GL}_{n}\times \,Y$
is equal to the subgroup
$B^{\times }{\hookrightarrow}\operatorname{GL}_{n}\times \,Y$
is equal to the subgroup
![]() $\operatorname{Stab}_{\operatorname{GL}_{n}}Y{\hookrightarrow}\operatorname{GL}_{n}\times Y$
.
$\operatorname{Stab}_{\operatorname{GL}_{n}}Y{\hookrightarrow}\operatorname{GL}_{n}\times Y$
.
Remark 1.65. Every algebroid
![]() $(X,A)$
, with
$(X,A)$
, with
![]() $A$
an algebra bundle, admits the tautological adjoint representation given by the adjoint representation of the algebra
$A$
an algebra bundle, admits the tautological adjoint representation given by the adjoint representation of the algebra
![]() $A$
on itself. By contrast, the representation of
$A$
on itself. By contrast, the representation of
![]() $A$
on itself by left multiplication is not an algebroid representation, unless
$A$
on itself by left multiplication is not an algebroid representation, unless
![]() $A=0$
.
$A=0$
.
Proposition 1.66. Every algebroid
![]() $(X,A)$
admits a stratification
$(X,A)$
admits a stratification
![]() $X^{\prime }\subset X$
such that the restricted algebroid
$X^{\prime }\subset X$
such that the restricted algebroid
![]() $(X^{\prime },A|_{X^{\prime }})$
admits a faithful representation.
$(X^{\prime },A|_{X^{\prime }})$
admits a faithful representation.
Proof. Without loss of generality, assume that
![]() $A$
is an algebra bundle with smooth unit group
$A$
is an algebra bundle with smooth unit group
![]() $A^{\times }$
and that
$A^{\times }$
and that
![]() $X$
is a connected isotrivial gerbe over the Deligne–Mumford stack
$X$
is a connected isotrivial gerbe over the Deligne–Mumford stack
![]() $S$
. Thus,
$S$
. Thus,
![]() $X\rightarrow S$
admits a section over a finite étale cover
$X\rightarrow S$
admits a section over a finite étale cover
![]() $S^{\prime }\rightarrow S$
.
$S^{\prime }\rightarrow S$
.
To begin with, we consider the case where
![]() $S^{\prime }=S$
, i.e., the case where
$S^{\prime }=S$
, i.e., the case where
![]() $X$
is a trivial gerbe over
$X$
is a trivial gerbe over
![]() $S$
. By Remark 1.43, we can assume that
$S$
. By Remark 1.43, we can assume that
![]() $A$
descends to
$A$
descends to
![]() $S$
and that we are dealing with the algebroid
$S$
and that we are dealing with the algebroid
![]() $(BA^{\times },A^{\times }\backslash A)$
. Then we can consider the representation of
$(BA^{\times },A^{\times }\backslash A)$
. Then we can consider the representation of
![]() $A$
on itself by left multiplication
$A$
on itself by left multiplication
![]() $\ell :A\rightarrow \operatorname{End}(A)$
. It restricts to a representation of
$\ell :A\rightarrow \operatorname{End}(A)$
. It restricts to a representation of
![]() $S$
-group schemes
$S$
-group schemes
![]() $\ell :A^{\times }\rightarrow \operatorname{GL}(A)$
. We get an induced morphism of algebraic stacks
$\ell :A^{\times }\rightarrow \operatorname{GL}(A)$
. We get an induced morphism of algebraic stacks
![]() $BA^{\times }\rightarrow B\operatorname{GL}(A)$
, which is covered by the morphism of algebras
$BA^{\times }\rightarrow B\operatorname{GL}(A)$
, which is covered by the morphism of algebras
![]() $A^{\times }\backslash A\rightarrow B\operatorname{GL}(A)\backslash \operatorname{End}(A)$
. Since
$A^{\times }\backslash A\rightarrow B\operatorname{GL}(A)\backslash \operatorname{End}(A)$
. Since
![]() $\ell :A\rightarrow \operatorname{End}(A)$
is injective, this gives the required faithful representation of
$\ell :A\rightarrow \operatorname{End}(A)$
is injective, this gives the required faithful representation of
![]() $(BA^{\times },A^{\times }\backslash A)$
.
$(BA^{\times },A^{\times }\backslash A)$
.
(Note that this construction does not contradict Remark 1.65. The vector bundle over
![]() $X$
defined by the left representation of
$X$
defined by the left representation of
![]() $A^{\times }$
on itself is different from the vector bundle underlying the algebroid
$A^{\times }$
on itself is different from the vector bundle underlying the algebroid
![]() $A$
over
$A$
over
![]() $X$
, which is given by the adjoint representation of
$X$
, which is given by the adjoint representation of
![]() $A^{\times }$
on itself.)
$A^{\times }$
on itself.)
Now consider the general case. The pullback
![]() $(X^{\prime },A^{\prime })$
of
$(X^{\prime },A^{\prime })$
of
![]() $(X,A)$
to
$(X,A)$
to
![]() $S^{\prime }$
is again an algebroid, as
$S^{\prime }$
is again an algebroid, as
![]() $X^{\prime }\rightarrow X$
is inert. Since
$X^{\prime }\rightarrow X$
is inert. Since
![]() $X^{\prime }\rightarrow S^{\prime }$
is a trivial gerbe,
$X^{\prime }\rightarrow S^{\prime }$
is a trivial gerbe,
![]() $(X^{\prime },A^{\prime })$
admits a faithful representation
$(X^{\prime },A^{\prime })$
admits a faithful representation
![]() $A^{\prime }\rightarrow \operatorname{End}(V)$
on a vector bundle
$A^{\prime }\rightarrow \operatorname{End}(V)$
on a vector bundle
![]() $V$
over
$V$
over
![]() $X^{\prime }$
. Let
$X^{\prime }$
. Let
![]() $\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the projection. Then,
$\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
be the projection. Then,
![]() $\unicode[STIX]{x1D70B}_{\ast }V$
is a faithful representation of
$\unicode[STIX]{x1D70B}_{\ast }V$
is a faithful representation of
![]() $A$
. In fact, by adjunction, the embedding
$A$
. In fact, by adjunction, the embedding
![]() $\unicode[STIX]{x1D70B}^{\ast }A\rightarrow \operatorname{End}(V)$
gives rise to an embedding
$\unicode[STIX]{x1D70B}^{\ast }A\rightarrow \operatorname{End}(V)$
gives rise to an embedding
![]() $A\rightarrow \unicode[STIX]{x1D70B}_{\ast }\operatorname{End}(V)\rightarrow \operatorname{End}(\unicode[STIX]{x1D70B}_{\ast }V)$
.◻
$A\rightarrow \unicode[STIX]{x1D70B}_{\ast }\operatorname{End}(V)\rightarrow \operatorname{End}(\unicode[STIX]{x1D70B}_{\ast }V)$
.◻
Clear algebroids
Suppose that
![]() $(X,A)$
is an algebroid and that
$(X,A)$
is an algebroid and that
![]() $X$
is a connected gerbe over the Deligne–Mumford stack
$X$
is a connected gerbe over the Deligne–Mumford stack
![]() $\overline{X}$
. Then the centre
$\overline{X}$
. Then the centre
![]() $Z(A)$
descends to a commutative finite type algebra over
$Z(A)$
descends to a commutative finite type algebra over
![]() $\overline{X}$
, by Lemma 1.20.
$\overline{X}$
, by Lemma 1.20.
Definition 1.67. We say an algebroid
![]() $(X,A)$
is clear, if:
$(X,A)$
is clear, if:
(i)
 $A$
and
$A$
and
 $Z(A)$
are algebra bundles over
$Z(A)$
are algebra bundles over
 $X$
;
$X$
;(ii)
 $X$
is a connected isotrivial gerbe over
$X$
is a connected isotrivial gerbe over
 $\overline{X}$
;
$\overline{X}$
;(iii) the Deligne–Mumford stack
 $\overline{X}$
is connected;
$\overline{X}$
is connected;(iv)
 $ZE(A)\rightarrow X$
is finite étale.
$ZE(A)\rightarrow X$
is finite étale.
For a clear algebroid,
![]() $ZE(A)$
and
$ZE(A)$
and
![]() $PZE(A)$
descend to finite étale
$PZE(A)$
descend to finite étale
![]() $\overline{X}$
-schemes. The definitions of central rank, split central rank, and central type apply to clear algebroids.
$\overline{X}$
-schemes. The definitions of central rank, split central rank, and central type apply to clear algebroids.
For every algebroid
![]() $(X,A)$
over a finite type algebraic stack
$(X,A)$
over a finite type algebraic stack
![]() $X$
, there exists a stratification of
$X$
, there exists a stratification of
![]() $X$
such that the restricted algebroids over the pieces of the stratification are all clear. This follows from Proposition 1.5 and Lemma 1.26.
$X$
such that the restricted algebroids over the pieces of the stratification are all clear. This follows from Proposition 1.5 and Lemma 1.26.
2 The spectrum of semi-simple inertia
Let
![]() $K(\text{DM})$
be the
$K(\text{DM})$
be the
![]() $\mathbb{Q}$
-vector space on (isomorphism classes of) finite type Deligne–Mumford stacks, modulo scissor relations and bundle relations, i.e., equations of the form
$\mathbb{Q}$
-vector space on (isomorphism classes of) finite type Deligne–Mumford stacks, modulo scissor relations and bundle relations, i.e., equations of the form
![]() $[Y]=[F\times X]$
, whenever
$[Y]=[F\times X]$
, whenever
![]() $Y\rightarrow X$
is a fibre bundle with special structure group and fibre
$Y\rightarrow X$
is a fibre bundle with special structure group and fibre
![]() $F$
. The product over the base scheme
$F$
. The product over the base scheme
![]() $\operatorname{Spec}R$
makes
$\operatorname{Spec}R$
makes
![]() $K(\text{DM})$
a
$K(\text{DM})$
a
![]() $\mathbb{Q}$
-algebra. We write
$\mathbb{Q}$
-algebra. We write
![]() $q$
for the class of the affine line in
$q$
for the class of the affine line in
![]() $K(\text{DM})$
.
$K(\text{DM})$
.
Let
![]() $\mathfrak{M}$
be a linear algebraic stack and
$\mathfrak{M}$
be a linear algebraic stack and
![]() $\mathfrak{A}\rightarrow \mathfrak{M}$
its universal endomorphism algebra. Recall that
$\mathfrak{A}\rightarrow \mathfrak{M}$
its universal endomorphism algebra. Recall that
![]() $(\mathfrak{M},\mathfrak{A})$
is an algebroid (cf. Example 1.40).
$(\mathfrak{M},\mathfrak{A})$
is an algebroid (cf. Example 1.40).
Stack functions
Definition 2.1. A stack function is a representable morphism of algebroids
![]() $(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
such that
$(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
such that
![]() $X$
is of finite type.
$X$
is of finite type.
The
![]() $K$
-module of
$K$
-module of
![]() $\mathfrak{M}$
, denoted by
$\mathfrak{M}$
, denoted by
![]() $K(\mathfrak{M})$
, is the free
$K(\mathfrak{M})$
, is the free
![]() $\mathbb{Q}$
-vector space on (isomorphism classes of) stack functions, modulo the scissor and bundle relations relative to
$\mathbb{Q}$
-vector space on (isomorphism classes of) stack functions, modulo the scissor and bundle relations relative to
![]() $(\mathfrak{M},\mathfrak{A})$
. The class in
$(\mathfrak{M},\mathfrak{A})$
. The class in
![]() $K(\mathfrak{M})$
defined by a stack function
$K(\mathfrak{M})$
defined by a stack function
![]() $X\rightarrow \mathfrak{M}$
will be denoted by
$X\rightarrow \mathfrak{M}$
will be denoted by
![]() $[X\rightarrow \mathfrak{M}]$
.
$[X\rightarrow \mathfrak{M}]$
.
A scissor relation relative to
![]() $\mathfrak{M}$
is
$\mathfrak{M}$
is
for any closed immersion of algebroids
![]() $Z{\hookrightarrow}X$
and any stack function
$Z{\hookrightarrow}X$
and any stack function
![]() $X\rightarrow \mathfrak{M}$
. The substacks
$X\rightarrow \mathfrak{M}$
. The substacks
![]() $Z$
and
$Z$
and
![]() $X\setminus Z$
are endowed with their respective pullback algebroids.
$X\setminus Z$
are endowed with their respective pullback algebroids.
A bundle relation relative to
![]() $\mathfrak{M}$
is
$\mathfrak{M}$
is
for any fibre bundle
![]() $Y\rightarrow X$
of algebroids with special structure group and fibre
$Y\rightarrow X$
of algebroids with special structure group and fibre
![]() $F$
, see Definition 1.53.
$F$
, see Definition 1.53.
There is an action of
![]() $K(\text{DM})$
on
$K(\text{DM})$
on
![]() $K(\mathfrak{M})$
, given by
$K(\mathfrak{M})$
, given by
This action makes
![]() $K(\mathfrak{M})$
into a
$K(\mathfrak{M})$
into a
![]() $K(\text{DM})$
-module.
$K(\text{DM})$
-module.
The additive zero in
![]() $K(\mathfrak{M})$
is given by the empty algebroid
$K(\mathfrak{M})$
is given by the empty algebroid
If
![]() $\mathfrak{M}$
admits a zero object (Definition 1.16), we denote the corresponding stack function by
$\mathfrak{M}$
admits a zero object (Definition 1.16), we denote the corresponding stack function by
![]() $1=[\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
. We can use it to embed
$1=[\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
. We can use it to embed
![]() $K(\text{DM})$
into
$K(\text{DM})$
into
![]() $K(\mathfrak{M})$
via
$K(\mathfrak{M})$
via
![]() $[X]\mapsto [X]\cdot 1=[X\rightarrow \operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
. We will always assume that
$[X]\mapsto [X]\cdot 1=[X\rightarrow \operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
. We will always assume that
![]() $\mathfrak{M}$
admits a zero object.
$\mathfrak{M}$
admits a zero object.
Remark 2.2. In the definition of
![]() $K(\mathfrak{M})$
, one can restrict to stack functions
$K(\mathfrak{M})$
, one can restrict to stack functions
![]() $X\rightarrow \mathfrak{M}$
, where
$X\rightarrow \mathfrak{M}$
, where
![]() $X$
is an algebroid bundle (by which we mean that
$X$
is an algebroid bundle (by which we mean that
![]() $A_{X}$
is an algebra bundle). For algebroid bundles, the definitions of locally closed immersion and fibre bundle simplify, because ‘inert’ is then a property of the underlying morphism of stacks (Remark 1.50), namely, that it pulls back from a morphism of Deligne–Mumford stacks (Proposition 1.48). Even the definition of algebroid itself simplifies in the case of algebroid bundles (Proposition 1.39).
$A_{X}$
is an algebra bundle). For algebroid bundles, the definitions of locally closed immersion and fibre bundle simplify, because ‘inert’ is then a property of the underlying morphism of stacks (Remark 1.50), namely, that it pulls back from a morphism of Deligne–Mumford stacks (Proposition 1.48). Even the definition of algebroid itself simplifies in the case of algebroid bundles (Proposition 1.39).
The filtration by split central rank
We say a stack function
![]() $X\rightarrow \mathfrak{M}$
is clear if
$X\rightarrow \mathfrak{M}$
is clear if
![]() $X$
is a clear algebroid (Definition 1.67).
$X$
is a clear algebroid (Definition 1.67).
Definition 2.3. We introduce the filtration by split central rank
![]() $K^{{\geqslant}k}(\mathfrak{M})$
on
$K^{{\geqslant}k}(\mathfrak{M})$
on
![]() $K(\mathfrak{M})$
by declaring
$K(\mathfrak{M})$
by declaring
![]() $K^{{\geqslant}k}(\mathfrak{M})$
to be generated as a
$K^{{\geqslant}k}(\mathfrak{M})$
to be generated as a
![]() $\mathbb{Q}$
-vector space by clear stack functions
$\mathbb{Q}$
-vector space by clear stack functions
![]() $[X\rightarrow \mathfrak{M}]$
such that
$[X\rightarrow \mathfrak{M}]$
such that
![]() $A_{X}$
admits
$A_{X}$
admits
![]() $k$
orthogonal central non-zero idempotents (globally).
$k$
orthogonal central non-zero idempotents (globally).
Alternatively,
![]() $K^{{\geqslant}k}(\mathfrak{M})$
is generated by
$K^{{\geqslant}k}(\mathfrak{M})$
is generated by
![]() $[X\rightarrow \mathfrak{M}]$
, where
$[X\rightarrow \mathfrak{M}]$
, where
![]() $X$
is a clear algebroid such that
$X$
is a clear algebroid such that
![]() $PZE(A_{X})$
has at least
$PZE(A_{X})$
has at least
![]() $k$
components.
$k$
components.
Each filtered piece
![]() $K^{{\geqslant}k}(\mathfrak{M})$
is stable under scalar multiplication by
$K^{{\geqslant}k}(\mathfrak{M})$
is stable under scalar multiplication by
![]() $K(\text{DM})$
. Let us introduce the abbreviation
$K(\text{DM})$
. Let us introduce the abbreviation
Remark 2.4. Trying to define a direct sum decomposition of
![]() $K(\mathfrak{M})$
by split central rank would not work, because a clear algebroid
$K(\mathfrak{M})$
by split central rank would not work, because a clear algebroid
![]() $X$
of split central rank
$X$
of split central rank
![]() $k$
may very well admit a closed substack
$k$
may very well admit a closed substack
![]() $Z\subset X$
whose restricted algebroid is again clear, but of split central rank larger than
$Z\subset X$
whose restricted algebroid is again clear, but of split central rank larger than
![]() $k$
. Similarly, the bundle relations do not respect split central rank.
$k$
. Similarly, the bundle relations do not respect split central rank.
The zero ring has no non-zero central idempotents, but any non-zero ring has at least one (namely, 1). For every stack function
![]() $X\rightarrow \mathfrak{M}$
, we have the closed substack
$X\rightarrow \mathfrak{M}$
, we have the closed substack
![]() $Z\subset X$
defined as the locus where
$Z\subset X$
defined as the locus where
![]() $1\in A_{X}$
vanishes. Then,
$1\in A_{X}$
vanishes. Then,
![]() $[X\rightarrow \mathfrak{M}]=[Z\rightarrow \mathfrak{M}]+[X\setminus Z\rightarrow \mathfrak{M}]$
, and
$[X\rightarrow \mathfrak{M}]=[Z\rightarrow \mathfrak{M}]+[X\setminus Z\rightarrow \mathfrak{M}]$
, and
![]() $[Z\rightarrow \mathfrak{M}]\in K(\text{DM})\subset K(\mathfrak{M})$
and
$[Z\rightarrow \mathfrak{M}]\in K(\text{DM})\subset K(\mathfrak{M})$
and
![]() $[X\setminus Z\rightarrow \mathfrak{M}]\in K^{{>}0}(\mathfrak{M})$
. Therefore,
$[X\setminus Z\rightarrow \mathfrak{M}]\in K^{{>}0}(\mathfrak{M})$
. Therefore,
![]() $K(\text{DM})\subset K(\mathfrak{M})$
is a complement for
$K(\text{DM})\subset K(\mathfrak{M})$
is a complement for
![]() $K^{{>}0}(\mathfrak{M})$
in
$K^{{>}0}(\mathfrak{M})$
in
![]() $K(\mathfrak{M})=K^{{\geqslant}0}(\mathfrak{M})$
, i.e.,
$K(\mathfrak{M})=K^{{\geqslant}0}(\mathfrak{M})$
, i.e.,
![]() $K(\mathfrak{M})=K(\text{DM})\oplus K^{{>}0}(\mathfrak{M})$
. In particular, we have
$K(\mathfrak{M})=K(\text{DM})\oplus K^{{>}0}(\mathfrak{M})$
. In particular, we have
2.1 The idempotent operators
 $E_{r}$
$E_{r}$
Let
![]() $E_{r}$
denote the operator on
$E_{r}$
denote the operator on
![]() $K(\mathfrak{M})$
which maps a stack function
$K(\mathfrak{M})$
which maps a stack function
![]() $[X\rightarrow \mathfrak{M}]$
to
$[X\rightarrow \mathfrak{M}]$
to
![]() $[E_{r}(X)\rightarrow X\rightarrow \mathfrak{M}]$
, where
$[E_{r}(X)\rightarrow X\rightarrow \mathfrak{M}]$
, where
![]() $E_{r}(X)=E_{r}(A_{X})$
is the stack of
$E_{r}(X)=E_{r}(A_{X})$
is the stack of
![]() $r$
-tuples of non-zero orthogonal idempotents adding to unity in
$r$
-tuples of non-zero orthogonal idempotents adding to unity in
![]() $A_{X}$
, see Definition 1.37. The algebroid structure on
$A_{X}$
, see Definition 1.37. The algebroid structure on
![]() $E_{r}(X)$
is described in Remark 1.60.
$E_{r}(X)$
is described in Remark 1.60.
The operators
![]() $E_{r}$
are well defined, because applying
$E_{r}$
are well defined, because applying
![]() $E_{r}$
to a stratification or a fibre bundle of algebroids gives rise to another inert morphism of algebroids of the same type. The operators
$E_{r}$
to a stratification or a fibre bundle of algebroids gives rise to another inert morphism of algebroids of the same type. The operators
![]() $E_{r}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
are
$E_{r}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
are
![]() $K(\text{DM})$
-linear.
$K(\text{DM})$
-linear.
This definition applies also to
![]() $r=0$
. The stack
$r=0$
. The stack
![]() $E_{0}(X)$
is empty if
$E_{0}(X)$
is empty if
![]() $A_{X}\not =0$
, and
$A_{X}\not =0$
, and
![]() $E_{0}(X)=X$
if
$E_{0}(X)=X$
if
![]() $X$
is a Deligne–Mumford stack. Hence,
$X$
is a Deligne–Mumford stack. Hence,
![]() $E_{0}$
is diagonalizable and has eigenvalues
$E_{0}$
is diagonalizable and has eigenvalues
![]() $0$
and
$0$
and
![]() $1$
. The kernel (
$1$
. The kernel (
![]() $0$
-eigenspaces) is
$0$
-eigenspaces) is
![]() $K^{{>}0}(\mathfrak{M})\subset K(\mathfrak{M})$
; the image (
$K^{{>}0}(\mathfrak{M})\subset K(\mathfrak{M})$
; the image (
![]() $1$
-eigenspaces) is denoted by
$1$
-eigenspaces) is denoted by
![]() $K^{0}(\mathfrak{M})\subset K(\mathfrak{M})$
and is generated by all stack functions
$K^{0}(\mathfrak{M})\subset K(\mathfrak{M})$
and is generated by all stack functions
![]() $[X\rightarrow \mathfrak{M}]$
, where
$[X\rightarrow \mathfrak{M}]$
, where
![]() $X$
is a Deligne–Mumford stack. In fact,
$X$
is a Deligne–Mumford stack. In fact,
![]() $K^{0}(\mathfrak{M})=K(\text{DM})\subset K(\mathfrak{M})$
.
$K^{0}(\mathfrak{M})=K(\text{DM})\subset K(\mathfrak{M})$
.
For
![]() $r=1$
, the operator
$r=1$
, the operator
![]() $E_{1}$
vanishes on stack functions
$E_{1}$
vanishes on stack functions
![]() $[X\rightarrow \mathfrak{M}]$
, where
$[X\rightarrow \mathfrak{M}]$
, where
![]() $X$
is a Deligne–Mumford stack, and acts as identity on stack functions for which
$X$
is a Deligne–Mumford stack, and acts as identity on stack functions for which
![]() $A_{X}\not =0$
. Hence,
$A_{X}\not =0$
. Hence,
![]() $E_{1}$
is also diagonalizable with eigenvalues
$E_{1}$
is also diagonalizable with eigenvalues
![]() $0$
and
$0$
and
![]() $1$
. The kernel of
$1$
. The kernel of
![]() $E_{1}$
is
$E_{1}$
is
![]() $K^{0}(\mathfrak{M})$
and the image is
$K^{0}(\mathfrak{M})$
and the image is
![]() $K^{{>}0}(\mathfrak{M})$
. Hence,
$K^{{>}0}(\mathfrak{M})$
. Hence,
![]() $E_{0}$
and
$E_{0}$
and
![]() $E_{1}$
are complementary idempotent operators on
$E_{1}$
are complementary idempotent operators on
![]() $K(\mathfrak{M})$
, i.e., they are orthogonal to each other and add up to the identity.
$K(\mathfrak{M})$
, i.e., they are orthogonal to each other and add up to the identity.
Recall the Stirling number of the second kind,
![]() $S(k,r)$
, which is defined in such a way that
$S(k,r)$
, which is defined in such a way that
![]() $r!\,S(k,r)$
is the number of surjections from
$r!\,S(k,r)$
is the number of surjections from
![]() $\text{}\underline{k}$
to
$\text{}\underline{k}$
to
![]() $\text{}\underline{r}$
. Here, and elsewhere, we write
$\text{}\underline{r}$
. Here, and elsewhere, we write
![]() $\text{}\underline{n}=\{1,\ldots ,n\}$
.
$\text{}\underline{n}=\{1,\ldots ,n\}$
.
Theorem 2.5. The operators
![]() $E_{r}$
, for all
$E_{r}$
, for all
![]() $r\geqslant 0$
, preserve the filtration
$r\geqslant 0$
, preserve the filtration
![]() $K^{{\geqslant}k}(\mathfrak{M})$
by split central rank. On the subquotient
$K^{{\geqslant}k}(\mathfrak{M})$
by split central rank. On the subquotient
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, the operator
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, the operator
![]() $E_{r}$
acts as multiplication by
$E_{r}$
acts as multiplication by
![]() $r!\,S(k,r)$
.
$r!\,S(k,r)$
.
Proof. Consider a clear algebroid
![]() $(X,A)$
with a morphism
$(X,A)$
with a morphism
![]() $X\rightarrow \mathfrak{M}$
defining the stack function
$X\rightarrow \mathfrak{M}$
defining the stack function
![]() $[X\rightarrow \mathfrak{M}]$
in
$[X\rightarrow \mathfrak{M}]$
in
![]() $K(\mathfrak{M})$
. Let
$K(\mathfrak{M})$
. Let
![]() $n$
be the central rank of
$n$
be the central rank of
![]() $X$
and
$X$
and
![]() $k$
the split central rank of
$k$
the split central rank of
![]() $X$
. The filtered piece
$X$
. The filtered piece
![]() $K^{{\geqslant}k}(\mathfrak{M})$
is generated by such
$K^{{\geqslant}k}(\mathfrak{M})$
is generated by such
![]() $[X\rightarrow \mathfrak{M}]$
.
$[X\rightarrow \mathfrak{M}]$
.
Denote by
![]() $X\rightarrow \overline{X}$
the coarse Deligne–Mumford stack of
$X\rightarrow \overline{X}$
the coarse Deligne–Mumford stack of
![]() $X$
. By assumption, both
$X$
. By assumption, both
![]() $X$
and
$X$
and
![]() $\overline{X}$
are connected and hence admit Grothendieck-style Galois theories (see [Reference NoohiNoo04, §4]).
$\overline{X}$
are connected and hence admit Grothendieck-style Galois theories (see [Reference NoohiNoo04, §4]).
Let
![]() $\widetilde{X}\rightarrow X$
be a connected Galois cover with Galois group
$\widetilde{X}\rightarrow X$
be a connected Galois cover with Galois group
![]() $\unicode[STIX]{x1D6E4}$
, which trivializes
$\unicode[STIX]{x1D6E4}$
, which trivializes
![]() $PZE(A)\rightarrow X$
. As
$PZE(A)\rightarrow X$
. As
![]() $PZE(A)$
descends to
$PZE(A)$
descends to
![]() $\overline{X}$
, this Galois cover can be constructed as a pullback from
$\overline{X}$
, this Galois cover can be constructed as a pullback from
![]() $\overline{X}$
. Therefore, the morphism
$\overline{X}$
. Therefore, the morphism
![]() $\widetilde{X}\rightarrow X$
is inert, and hence
$\widetilde{X}\rightarrow X$
is inert, and hence
![]() $\widetilde{X}$
inherits, via pullback, the structure of an algebroid, and hence
$\widetilde{X}$
inherits, via pullback, the structure of an algebroid, and hence
![]() $[\widetilde{X}\rightarrow X\rightarrow \mathfrak{M}]$
is a stack function.
$[\widetilde{X}\rightarrow X\rightarrow \mathfrak{M}]$
is a stack function.
Recall that the degree of the cover
![]() $PZE(A)\rightarrow X$
is
$PZE(A)\rightarrow X$
is
![]() $n$
, and the number of components of
$n$
, and the number of components of
![]() $PZE(A)$
is
$PZE(A)$
is
![]() $k$
.
$k$
.
By labelling the components of the pullback of
![]() $PZE(A)$
to
$PZE(A)$
to
![]() $\widetilde{X}$
, we obtain an action of
$\widetilde{X}$
, we obtain an action of
![]() $\unicode[STIX]{x1D6E4}$
on the set
$\unicode[STIX]{x1D6E4}$
on the set
![]() $\text{}\underline{n}=\{1,\ldots ,n\}$
and an isomorphism of finite étale covers of
$\text{}\underline{n}=\{1,\ldots ,n\}$
and an isomorphism of finite étale covers of
![]() $X$
$X$
Both source and target of this isomorphism support natural algebroids and the isomorphism preserves them. The number of orbits of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\text{}\underline{n}$
is
$\text{}\underline{n}$
is
![]() $k$
.
$k$
.
Then we also have an isomorphism
 $$\begin{eqnarray}\displaystyle \widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r}) & \stackrel{\simeq }{\longrightarrow } & \displaystyle ZE_{r}(A)\nonumber\\ \displaystyle \hspace{0.0pt}[x,\unicode[STIX]{x1D711}] & \longmapsto & \displaystyle \biggl(\mathop{\sum }_{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D70C}}e_{[x,\unicode[STIX]{x1D708}]}\biggr)_{\unicode[STIX]{x1D70C}=1,\ldots ,r},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r}) & \stackrel{\simeq }{\longrightarrow } & \displaystyle ZE_{r}(A)\nonumber\\ \displaystyle \hspace{0.0pt}[x,\unicode[STIX]{x1D711}] & \longmapsto & \displaystyle \biggl(\mathop{\sum }_{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D70C}}e_{[x,\unicode[STIX]{x1D708}]}\biggr)_{\unicode[STIX]{x1D70C}=1,\ldots ,r},\nonumber\end{eqnarray}$$
where
![]() $ZE_{r}$
denotes the stack of labelled complete sets of
$ZE_{r}$
denotes the stack of labelled complete sets of
![]() $r$
orthogonal central idempotents. Again, both stacks involved are in fact algebroids, and this isomorphism is an isomorphism of algebroids.
$r$
orthogonal central idempotents. Again, both stacks involved are in fact algebroids, and this isomorphism is an isomorphism of algebroids.
Hence, we may calculate as follows (all stacks involved are endowed with their natural algebroid structures):
 $$\begin{eqnarray}\displaystyle ZE_{r}[X\rightarrow \mathfrak{M}] & = & \displaystyle [\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})\rightarrow \mathfrak{M}]\nonumber\\ \displaystyle & = & \displaystyle \biggl[\widetilde{X}{\times _{\unicode[STIX]{x1D6E4}}\coprod }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6E4}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4}}[\widetilde{X}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})^{\unicode[STIX]{x1D6E4}}}[X\rightarrow \mathfrak{M}]+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4} \\ \operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\not =\unicode[STIX]{x1D6E4}}}[\widetilde{X}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle ZE_{r}[X\rightarrow \mathfrak{M}] & = & \displaystyle [\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})\rightarrow \mathfrak{M}]\nonumber\\ \displaystyle & = & \displaystyle \biggl[\widetilde{X}{\times _{\unicode[STIX]{x1D6E4}}\coprod }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6E4}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}\biggr]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4}}[\widetilde{X}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})^{\unicode[STIX]{x1D6E4}}}[X\rightarrow \mathfrak{M}]+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D711}\in \operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})/\unicode[STIX]{x1D6E4} \\ \operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\not =\unicode[STIX]{x1D6E4}}}[\widetilde{X}/\operatorname{Stab}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D711}\rightarrow \mathfrak{M}].\nonumber\end{eqnarray}$$
Now, we have
![]() $\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})^{\unicode[STIX]{x1D6E4}}=\operatorname{Epi}(\text{}\underline{n}/\unicode[STIX]{x1D6E4},\text{}\underline{r})$
, and hence
$\operatorname{Epi}(\text{}\underline{n},\text{}\underline{r})^{\unicode[STIX]{x1D6E4}}=\operatorname{Epi}(\text{}\underline{n}/\unicode[STIX]{x1D6E4},\text{}\underline{r})$
, and hence
Thus, we conclude,
For any proper subgroup
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
, the quotient
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
, the quotient
![]() $X^{\prime }=\widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is an intermediate cover
$X^{\prime }=\widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is an intermediate cover
![]() $\widetilde{X}\rightarrow X^{\prime }\rightarrow X$
such that
$\widetilde{X}\rightarrow X^{\prime }\rightarrow X$
such that
![]() $X^{\prime }\not =X$
. The pullback of
$X^{\prime }\not =X$
. The pullback of
![]() $PZE(A)$
to
$PZE(A)$
to
![]() $X^{\prime }$
has more than
$X^{\prime }$
has more than
![]() $k$
components, because the number of orbits of
$k$
components, because the number of orbits of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
on
$\unicode[STIX]{x1D6E4}^{\prime }$
on
![]() $\text{}\underline{n}$
is larger than
$\text{}\underline{n}$
is larger than
![]() $k$
. Thus, we have proved the theorem for
$k$
. Thus, we have proved the theorem for
![]() $ZE_{r}$
, instead of
$ZE_{r}$
, instead of
![]() $E_{r}$
.
$E_{r}$
.
Now, observe that
![]() $ZE_{r}(A)\subset E_{r}(A)$
is a closed substack, because
$ZE_{r}(A)\subset E_{r}(A)$
is a closed substack, because
![]() $ZE_{r}(A)\rightarrow X$
is proper and
$ZE_{r}(A)\rightarrow X$
is proper and
![]() $E_{r}(A)\rightarrow X$
is separated. So we can write
$E_{r}(A)\rightarrow X$
is separated. So we can write
where
![]() $NZE_{r}(A)$
is the complement of
$NZE_{r}(A)$
is the complement of
![]() $ZE_{r}(A)$
in
$ZE_{r}(A)$
in
![]() $E_{r}(A)$
. To prove that
$E_{r}(A)$
. To prove that
![]() $[NZE_{r}(A)\rightarrow \mathfrak{M}]\in K^{{>}k}(\mathfrak{M})$
, let
$[NZE_{r}(A)\rightarrow \mathfrak{M}]\in K^{{>}k}(\mathfrak{M})$
, let
![]() $Y{\hookrightarrow}NZE_{r}(A)$
be a locally closed embedding such that
$Y{\hookrightarrow}NZE_{r}(A)$
be a locally closed embedding such that
![]() $(E_{r}(A),A^{\text{fix}})|_{Y}$
is a clear algebroid.
$(E_{r}(A),A^{\text{fix}})|_{Y}$
is a clear algebroid.
Consider the embedding of algebras
![]() $A^{\text{fix}}|_{Y}{\hookrightarrow}A|_{Y}$
. It induces an embedding of commutative algebras
$A^{\text{fix}}|_{Y}{\hookrightarrow}A|_{Y}$
. It induces an embedding of commutative algebras
![]() $Z(A|_{Y}){\hookrightarrow}Z(A^{\text{fix}}|_{Y})$
, because
$Z(A|_{Y}){\hookrightarrow}Z(A^{\text{fix}}|_{Y})$
, because
![]() $Z(A|_{Y})\subset A^{\text{fix}}|_{Y}$
. The algebra
$Z(A|_{Y})\subset A^{\text{fix}}|_{Y}$
. The algebra
![]() $A|_{Y}$
comes with
$A|_{Y}$
comes with
![]() $r$
tautological idempotent sections, all of which are contained in
$r$
tautological idempotent sections, all of which are contained in
![]() $Z(A^{\text{fix}}|_{Y})$
, but at least one of which is not contained in
$Z(A^{\text{fix}}|_{Y})$
, but at least one of which is not contained in
![]() $Z(A|_{Y})$
. So, by Proposition 1.36(ii), the split central rank of
$Z(A|_{Y})$
. So, by Proposition 1.36(ii), the split central rank of
![]() $A^{\text{fix}}|_{Y}$
is strictly larger than the split central rank of
$A^{\text{fix}}|_{Y}$
is strictly larger than the split central rank of
![]() $A|_{Y}$
. The latter is at least as big as
$A|_{Y}$
. The latter is at least as big as
![]() $k$
, the split central rank of
$k$
, the split central rank of
![]() $A$
, because the split central rank cannot decrease under base extension. This shows that
$A$
, because the split central rank cannot decrease under base extension. This shows that
![]() $[Y\rightarrow \mathfrak{M}]\in K^{{>}k}(\mathfrak{M})$
and finishes the proof.◻
$[Y\rightarrow \mathfrak{M}]\in K^{{>}k}(\mathfrak{M})$
and finishes the proof.◻
Corollary 2.6. The operators
![]() $E_{r}$
, for
$E_{r}$
, for
![]() $r\geqslant 0$
are simultaneously diagonalizable. The common eigenspaces form a family
$r\geqslant 0$
are simultaneously diagonalizable. The common eigenspaces form a family
![]() $K^{k}(\mathfrak{M})$
of subspaces of
$K^{k}(\mathfrak{M})$
of subspaces of
![]() $K(\mathfrak{M})$
indexed by non-negative integers
$K(\mathfrak{M})$
indexed by non-negative integers
![]() $k\geqslant 0$
, and
$k\geqslant 0$
, and
Moreover, for every
![]() $r\geqslant 0$
,
$r\geqslant 0$
,
Let
![]() $\unicode[STIX]{x1D70B}_{k}$
denote the projection onto
$\unicode[STIX]{x1D70B}_{k}$
denote the projection onto
![]() $K^{k}(\mathfrak{M})$
. We have
$K^{k}(\mathfrak{M})$
. We have
for all
![]() $r\geqslant 0$
,
$r\geqslant 0$
,
![]() $k\geqslant 0$
.
$k\geqslant 0$
.
Proof. First remark that for given
![]() $r$
, the numbers
$r$
, the numbers
![]() $r!\,S(k,r)$
form a monotone increasing sequence of integers.
$r!\,S(k,r)$
form a monotone increasing sequence of integers.
Then note that the operators
![]() $E_{r}$
pairwise commute: the composition
$E_{r}$
pairwise commute: the composition
![]() $E_{r}\circ E_{r^{\prime }}$
associates to an algebroid
$E_{r}\circ E_{r^{\prime }}$
associates to an algebroid
![]() $(X,A)$
the stack of pairs
$(X,A)$
the stack of pairs
![]() $(e,e^{\prime })$
, where both
$(e,e^{\prime })$
, where both
![]() $e$
and
$e$
and
![]() $e^{\prime }$
are complete families of non-zero orthogonal idempotents in
$e^{\prime }$
are complete families of non-zero orthogonal idempotents in
![]() $A$
, the length of
$A$
, the length of
![]() $e$
being
$e$
being
![]() $r$
, the length of
$r$
, the length of
![]() $e^{\prime }$
being
$e^{\prime }$
being
![]() $r^{\prime }$
, and the members of
$r^{\prime }$
, and the members of
![]() $e$
commuting with the members of
$e$
commuting with the members of
![]() $e^{\prime }$
.
$e^{\prime }$
.
Finally, let us prove that for every
![]() $k$
and every
$k$
and every
![]() $r$
, the
$r$
, the
![]() $\mathbb{Q}$
-vector space
$\mathbb{Q}$
-vector space
![]() $K^{{\geqslant}k}(\mathfrak{M})$
is a union of finite-dimensional subspaces invariant by
$K^{{\geqslant}k}(\mathfrak{M})$
is a union of finite-dimensional subspaces invariant by
![]() $E_{r}$
.
$E_{r}$
.
For this, define
![]() $K(\mathfrak{M})_{{\leqslant}N}$
to be generated as a
$K(\mathfrak{M})_{{\leqslant}N}$
to be generated as a
![]() $\mathbb{Q}$
-vector space by stack functions
$\mathbb{Q}$
-vector space by stack functions
![]() $[X\rightarrow \mathfrak{M}]$
, where
$[X\rightarrow \mathfrak{M}]$
, where
![]() $X$
is a clear algebroid, such that the rank of the vector bundle underlying the algebra
$X$
is a clear algebroid, such that the rank of the vector bundle underlying the algebra
![]() $A_{X}\rightarrow X$
is bounded above by
$A_{X}\rightarrow X$
is bounded above by
![]() $N$
. This is an ascending filtration of
$N$
. This is an ascending filtration of
![]() $K(\mathfrak{M})$
, which is preserved by
$K(\mathfrak{M})$
, which is preserved by
![]() $E_{r}$
. Set
$E_{r}$
. Set
Suppose
![]() $x=[X\rightarrow \mathfrak{M}]$
is a stack function with
$x=[X\rightarrow \mathfrak{M}]$
is a stack function with
![]() $X$
a clear algebroid of split central rank
$X$
a clear algebroid of split central rank
![]() $k$
, and let
$k$
, and let
![]() $N$
be the rank of the vector bundle underlying
$N$
be the rank of the vector bundle underlying
![]() $A_{X}$
. Note that
$A_{X}$
. Note that
![]() $k\leqslant N$
, because for a commutative algebra, the number of primitive idempotents is bounded by the rank of the underlying vector bundle. We deduce that for
$k\leqslant N$
, because for a commutative algebra, the number of primitive idempotents is bounded by the rank of the underlying vector bundle. We deduce that for
![]() $k>N$
, we have
$k>N$
, we have
![]() $K^{{\geqslant}k}(\mathfrak{M})_{{\leqslant}N}=0$
.
$K^{{\geqslant}k}(\mathfrak{M})_{{\leqslant}N}=0$
.
On the other hand, Theorem 2.5 implies by induction that
Applying this for
![]() $i=N-k+1$
, we see that
$i=N-k+1$
, we see that
and hence that
![]() $\mathbb{Q}\,x+\mathbb{Q}\,E_{r}(x)+\cdots +\mathbb{Q}\,E_{r}^{N-k}(x)$
is invariant under
$\mathbb{Q}\,x+\mathbb{Q}\,E_{r}(x)+\cdots +\mathbb{Q}\,E_{r}^{N-k}(x)$
is invariant under
![]() $E_{r}$
.
$E_{r}$
.
This proves that any
![]() $x\in K^{{\geqslant}k}(\mathfrak{M})$
is contained in a finite-dimensional subspace invariant under
$x\in K^{{\geqslant}k}(\mathfrak{M})$
is contained in a finite-dimensional subspace invariant under
![]() $E_{r}$
. Standard techniques from finite-dimensional linear algebra over
$E_{r}$
. Standard techniques from finite-dimensional linear algebra over
![]() $\mathbb{Q}$
now imply the result.◻
$\mathbb{Q}$
now imply the result.◻
Remark 2.7. The proof of Theorem 2.5 and its corollary show that the central versions
![]() $ZE_{r}$
of the
$ZE_{r}$
of the
![]() $E_{r}$
are also diagonalizable. On the other hand, the
$E_{r}$
are also diagonalizable. On the other hand, the
![]() $ZE_{r}$
do not commute with each other, and so are less useful.
$ZE_{r}$
do not commute with each other, and so are less useful.
Corollary 2.8. For
![]() $r\geqslant 1$
, we have
$r\geqslant 1$
, we have
In particular, for any
![]() $x\in K(\mathfrak{M})$
, we have
$x\in K(\mathfrak{M})$
, we have
![]() $E_{r}x=0$
for
$E_{r}x=0$
for
![]() $r\gg 0$
.
$r\gg 0$
.
Corollary 2.9. For every
![]() $k\geqslant 0$
, we have
$k\geqslant 0$
, we have
where the
![]() $s(n,k)$
are the Stirling numbers of the first kind. In particular,
$s(n,k)$
are the Stirling numbers of the first kind. In particular,
![]() $\unicode[STIX]{x1D70B}_{0}=E_{0}$
, and
$\unicode[STIX]{x1D70B}_{0}=E_{0}$
, and
Proof. We have
and hence
and therefore
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{r\geqslant 0}\frac{s(r,k)}{r!}\,E_{r} & = & \displaystyle \mathop{\sum }_{r\geqslant 0}\frac{s(r,k)}{r!}\mathop{\sum }_{\ell \geqslant 0}r!\,S(\ell ,r)\,\unicode[STIX]{x1D70B}_{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell \geqslant 0}\biggl(\mathop{\sum }_{r\geqslant 0}S(\ell ,r)s(r,k)\biggr)\,\unicode[STIX]{x1D70B}_{\ell }=\mathop{\sum }_{\ell \geqslant 0}\unicode[STIX]{x1D6FF}_{\ell ,k}\,\unicode[STIX]{x1D70B}_{\ell }=\unicode[STIX]{x1D70B}_{k},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{r\geqslant 0}\frac{s(r,k)}{r!}\,E_{r} & = & \displaystyle \mathop{\sum }_{r\geqslant 0}\frac{s(r,k)}{r!}\mathop{\sum }_{\ell \geqslant 0}r!\,S(\ell ,r)\,\unicode[STIX]{x1D70B}_{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell \geqslant 0}\biggl(\mathop{\sum }_{r\geqslant 0}S(\ell ,r)s(r,k)\biggr)\,\unicode[STIX]{x1D70B}_{\ell }=\mathop{\sum }_{\ell \geqslant 0}\unicode[STIX]{x1D6FF}_{\ell ,k}\,\unicode[STIX]{x1D70B}_{\ell }=\unicode[STIX]{x1D70B}_{k},\nonumber\end{eqnarray}$$
by the inverse relationship between the Stirling numbers of the first and second kind. ◻
Remark 2.10. The Stirling numbers of the first kind appear in the Taylor expansions of the powers of the logarithm:
Definition 2.11. Let
![]() $t$
be a formal variable. We define the operator
$t$
be a formal variable. We define the operator
by the formula
and extending
![]() $K(\text{DM})[t]$
-linearly. We can write, formally,
$K(\text{DM})[t]$
-linearly. We can write, formally,
Remark 2.12. We have the following convenient formula:
It follows from Corollary 2.9, using the identity
Example 2.13. The universal rank 2 vector bundle
![]() $\operatorname{GL}_{2}\backslash \mathbb{A}^{2}\rightarrow B\operatorname{GL}_{2}$
and its classifying morphism to
$\operatorname{GL}_{2}\backslash \mathbb{A}^{2}\rightarrow B\operatorname{GL}_{2}$
and its classifying morphism to
![]() $\mathfrak{Vect}$
define a Hall algebra element
$\mathfrak{Vect}$
define a Hall algebra element
![]() $[B\operatorname{GL}_{2}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
, which we will abbreviate to
$[B\operatorname{GL}_{2}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
, which we will abbreviate to
![]() $[B\operatorname{GL}_{2}]$
. To decompose
$[B\operatorname{GL}_{2}]$
. To decompose
![]() $[B\operatorname{GL}_{2}]$
into its pieces according to (12), we consider the action of
$[B\operatorname{GL}_{2}]$
into its pieces according to (12), we consider the action of
![]() $E_{2}$
, as we have
$E_{2}$
, as we have
![]() $E_{r}[B\operatorname{GL}_{2}]=0$
for all
$E_{r}[B\operatorname{GL}_{2}]=0$
for all
![]() $r>2$
. In fact,
$r>2$
. In fact,
where
![]() $T$
is a maximal torus in
$T$
is a maximal torus in
![]() $\operatorname{GL}_{2}$
. Thus,
$\operatorname{GL}_{2}$
. Thus,
![]() $\mathbb{Q}[B\operatorname{GL}_{2}]+\,\mathbb{Q}[BT]$
is a subspace of
$\mathbb{Q}[B\operatorname{GL}_{2}]+\,\mathbb{Q}[BT]$
is a subspace of
![]() $K(\mathfrak{Vect})$
invariant under
$K(\mathfrak{Vect})$
invariant under
![]() $E_{2}$
, and the matrix of
$E_{2}$
, and the matrix of
![]() $E_{2}$
acting on this subspace is
$E_{2}$
acting on this subspace is
This matrix is lower triangular, with different numbers on the diagonal, and hence diagonalizable over
![]() $\mathbb{Q}$
. In fact, the diagonal entries are
$\mathbb{Q}$
. In fact, the diagonal entries are
![]() $2\,S(1,2)=0$
and
$2\,S(1,2)=0$
and
![]() $2\,S(2,2)=2$
, as predicted by Theorem 2.5, with
$2\,S(2,2)=2$
, as predicted by Theorem 2.5, with
![]() $r=2$
and
$r=2$
and
![]() $k=1,2$
. Diagonalizing (13) gives the eigenvectors
$k=1,2$
. Diagonalizing (13) gives the eigenvectors
(i)
 $v_{1}=[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
with eigenvalue
$v_{1}=[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
with eigenvalue
 $0$
,
$0$
,(ii)
 $v_{2}=\frac{1}{2}[BT]$
with eigenvalue
$v_{2}=\frac{1}{2}[BT]$
with eigenvalue
 $2$
.
$2$
.
Therefore, we have
![]() $v_{1}\in K^{1}(\mathfrak{Vect})$
and
$v_{1}\in K^{1}(\mathfrak{Vect})$
and
![]() $v_{2}\in K^{2}(\mathfrak{Vect})$
, and since
$v_{2}\in K^{2}(\mathfrak{Vect})$
, and since
![]() $[B\operatorname{GL}_{2}]=v_{1}+v_{2}$
, we have found the required decomposition of
$[B\operatorname{GL}_{2}]=v_{1}+v_{2}$
, we have found the required decomposition of
![]() $[B\operatorname{GL}_{2}]$
, as noted in Corollary 2.9.
$[B\operatorname{GL}_{2}]$
, as noted in Corollary 2.9.
2.2 The spectrum of semi-simple inertia
The connected semi-simple inertia operator on
![]() $K(\mathfrak{M})$
is the
$K(\mathfrak{M})$
is the
![]() $\mathbb{Q}$
-linear endomorphism
$\mathbb{Q}$
-linear endomorphism
Here,
![]() $I_{X}^{\circ ,\text{ss}}=A_{X}^{\times ,\text{ss}}$
denotes the semi-simple algebroid inertia of the algebroid
$I_{X}^{\circ ,\text{ss}}=A_{X}^{\times ,\text{ss}}$
denotes the semi-simple algebroid inertia of the algebroid
![]() $X$
, see Remark 1.58. Note that
$X$
, see Remark 1.58. Note that
![]() $I^{\circ ,\text{ss}}$
respects the scissor and bundle relations defining
$I^{\circ ,\text{ss}}$
respects the scissor and bundle relations defining
![]() $K(\mathfrak{M})$
and is linear over
$K(\mathfrak{M})$
and is linear over
![]() $K(\text{DM})$
, because passing to connected inertia commutes with inert pullbacks.
$K(\text{DM})$
, because passing to connected inertia commutes with inert pullbacks.
Note that
![]() $I^{\circ ,\text{ss}}$
commutes with
$I^{\circ ,\text{ss}}$
commutes with
![]() $E_{r}$
for every
$E_{r}$
for every
![]() $r$
. Both compositions
$r$
. Both compositions
![]() $E_{r}\circ I^{\circ ,ss}$
and
$E_{r}\circ I^{\circ ,ss}$
and
![]() $I^{\circ ,\text{ss}}\circ E_{r}$
associate to an algebroid
$I^{\circ ,\text{ss}}\circ E_{r}$
associate to an algebroid
![]() $(X,A)$
the stack of pairs
$(X,A)$
the stack of pairs
![]() $(e,a)$
, where
$(e,a)$
, where
![]() $a$
is a semi-simple unit in
$a$
is a semi-simple unit in
![]() $A$
and
$A$
and
![]() $e$
is a labelled complete set of
$e$
is a labelled complete set of
![]() $r$
orthogonal idempotents in
$r$
orthogonal idempotents in
![]() $A$
, all commuting with
$A$
, all commuting with
![]() $a$
. In particular,
$a$
. In particular,
![]() $I^{\circ ,\text{ss}}$
preserves the filtration of
$I^{\circ ,\text{ss}}$
preserves the filtration of
![]() $K(\mathfrak{M})$
by split central rank.
$K(\mathfrak{M})$
by split central rank.
In the following, we will need an auxiliary construction. Fix
![]() $k\geqslant 0$
. For an algebroid
$k\geqslant 0$
. For an algebroid
![]() $(X,A)$
, let
$(X,A)$
, let
![]() $Y=E_{k}(A)$
and
$Y=E_{k}(A)$
and
![]() $(Y,B)$
be the algebroid structure on
$(Y,B)$
be the algebroid structure on
![]() $Y$
(see 1.60). The algebra
$Y$
(see 1.60). The algebra
![]() $B$
comes with a complete set of
$B$
comes with a complete set of
![]() $k$
orthogonal idempotents, and we divide
$k$
orthogonal idempotents, and we divide
![]() $B^{\times ,\text{ss}}$
by the induced action of
$B^{\times ,\text{ss}}$
by the induced action of
![]() $\mathbb{G}_{m}^{k}$
, as treated in Proposition 1.61, to get
$\mathbb{G}_{m}^{k}$
, as treated in Proposition 1.61, to get
![]() $\widetilde{B}^{\times ,\text{ss}}$
. Let us write
$\widetilde{B}^{\times ,\text{ss}}$
. Let us write
We may think of
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}X$
as the stack of triples
$\widetilde{I}_{k}^{\circ ,\text{ss}}X$
as the stack of triples
![]() $(x,e,[a])$
, where
$(x,e,[a])$
, where
![]() $x$
is a point of
$x$
is a point of
![]() $X$
,
$X$
,
![]() $e=(e_{1},\ldots ,e_{k})$
is a labelled complete set of orthogonal idempotents in
$e=(e_{1},\ldots ,e_{k})$
is a labelled complete set of orthogonal idempotents in
![]() $A_{x}$
, and
$A_{x}$
, and
![]() $[a]$
is an equivalence class of semi-simple units in
$[a]$
is an equivalence class of semi-simple units in
![]() $A_{x}^{e_{1},\ldots ,e_{k}}$
, where
$A_{x}^{e_{1},\ldots ,e_{k}}$
, where
![]() $a\sim \sum _{i=1}^{k}\unicode[STIX]{x1D706}_{i}e_{i}\,a$
, for
$a\sim \sum _{i=1}^{k}\unicode[STIX]{x1D706}_{i}e_{i}\,a$
, for
![]() $\unicode[STIX]{x1D706}_{i}\in \mathscr{O}_{X}|_{x}$
(although this neglects the sheafification inherent in the quotient construction). We have structure morphisms
$\unicode[STIX]{x1D706}_{i}\in \mathscr{O}_{X}|_{x}$
(although this neglects the sheafification inherent in the quotient construction). We have structure morphisms
This construction gives rise to a
![]() $K(\text{DM})$
-linear operator
$K(\text{DM})$
-linear operator
Recall that
![]() $q=[\mathbb{A}^{1}]$
. The composition
$q=[\mathbb{A}^{1}]$
. The composition
![]() $I^{\circ ,\text{ss}}\circ E_{r}$
is divisible by
$I^{\circ ,\text{ss}}\circ E_{r}$
is divisible by
![]() $(q-1)^{r}$
, as shown by the following proposition.
$(q-1)^{r}$
, as shown by the following proposition.
Proposition 2.14. For every
![]() $k\geqslant 0$
, we have
$k\geqslant 0$
, we have
as
![]() $K(\text{DM})$
-linear operators on
$K(\text{DM})$
-linear operators on
![]() $K(\mathfrak{M})$
.
$K(\mathfrak{M})$
.
Proof. We have
because of the bundle relations in
![]() $K(\mathfrak{M})$
, see Proposition 1.61.◻
$K(\mathfrak{M})$
, see Proposition 1.61.◻
Corollary 2.15. The map which
![]() $I^{\circ ,\text{ss}}$
induces on the subquotient
$I^{\circ ,\text{ss}}$
induces on the subquotient
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
is divisible by
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
is divisible by
![]() $(q-1)^{k}$
:
$(q-1)^{k}$
:
Proof. This is because on
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, the operator
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, the operator
![]() $E_{k}$
acts as multiplication by
$E_{k}$
acts as multiplication by
![]() $k!$
.◻
$k!$
.◻
We will use as scalars the localization of
![]() $\mathbb{Q}[q]$
at the maximal ideal
$\mathbb{Q}[q]$
at the maximal ideal
![]() $(q-1)$
, denoted by
$(q-1)$
, denoted by
![]() $\mathbb{Q}[q]_{(q-1)}$
, thus inverting all rational polynomials in
$\mathbb{Q}[q]_{(q-1)}$
, thus inverting all rational polynomials in
![]() $q$
that do not vanish at
$q$
that do not vanish at
![]() $q=1$
. We extend scalars on
$q=1$
. We extend scalars on
![]() $K(\mathfrak{M})$
as well, and consider
$K(\mathfrak{M})$
as well, and consider
Note that this definition ensures that
![]() $K(\mathfrak{M})_{(q-1)}$
is
$K(\mathfrak{M})_{(q-1)}$
is
![]() $(q-1)$
-torsion free. The direct sum decomposition (12) extends to
$(q-1)$
-torsion free. The direct sum decomposition (12) extends to
![]() $K(\mathfrak{M})_{(q-1)}$
, and the operator
$K(\mathfrak{M})_{(q-1)}$
, and the operator
![]() $I^{\circ ,\text{ss}}$
extends to a
$I^{\circ ,\text{ss}}$
extends to a
![]() $\mathbb{Q}[q]_{(q-1)}$
-linear operator
$\mathbb{Q}[q]_{(q-1)}$
-linear operator
For a partition
![]() $\unicode[STIX]{x1D706}\vdash n$
, we denote its length (i.e., the number of its parts) by
$\unicode[STIX]{x1D706}\vdash n$
, we denote its length (i.e., the number of its parts) by
![]() $\ell (\unicode[STIX]{x1D706})$
. We define
$\ell (\unicode[STIX]{x1D706})$
. We define
This is a polynomial in
![]() $q$
of degree
$q$
of degree
![]() $n$
that vanishes to order
$n$
that vanishes to order
![]() $\ell (\unicode[STIX]{x1D706})$
at
$\ell (\unicode[STIX]{x1D706})$
at
![]() $q=1$
. We also define
$q=1$
. We also define
This is a polynomial in
![]() $q$
that is invertible in
$q$
that is invertible in
![]() $\mathbb{Q}[q]_{(q-1)}$
.
$\mathbb{Q}[q]_{(q-1)}$
.
Theorem 2.16. The operator
is diagonalizable. Its eigenvalue spectrum consists of all
![]() $\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}$
, for partitions
$\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}$
, for partitions
![]() $\unicode[STIX]{x1D706}$
of length
$\unicode[STIX]{x1D706}$
of length
![]() $\ell (\unicode[STIX]{x1D706})=k$
.
$\ell (\unicode[STIX]{x1D706})=k$
.
Proof. We will fix
![]() $k$
and work throughout in the subquotient
$k$
and work throughout in the subquotient
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
, restricting all operators tacitly to this subquotient. Note that, as a
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
, restricting all operators tacitly to this subquotient. Note that, as a
![]() $\mathbb{Q}[q]_{(q-1)}$
-module,
$\mathbb{Q}[q]_{(q-1)}$
-module,
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
is isomorphic to
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
is isomorphic to
![]() $K^{k}(\mathfrak{M})_{(q-1)}$
and is hence
$K^{k}(\mathfrak{M})_{(q-1)}$
and is hence
![]() $(q-1)$
-torsion free.
$(q-1)$
-torsion free.
We order partitions of length
![]() $k$
by divisibility. If
$k$
by divisibility. If
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
are partitions with
$\unicode[STIX]{x1D707}$
are partitions with
![]() $\ell (\unicode[STIX]{x1D706})=k$
and
$\ell (\unicode[STIX]{x1D706})=k$
and
![]() $\ell (\unicode[STIX]{x1D707})=k$
, we write
$\ell (\unicode[STIX]{x1D707})=k$
, we write
![]() $\unicode[STIX]{x1D706}\mid \unicode[STIX]{x1D707}$
if there exists a permutation
$\unicode[STIX]{x1D706}\mid \unicode[STIX]{x1D707}$
if there exists a permutation
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\text{}\underline{k}$
such that
$\text{}\underline{k}$
such that
![]() $\unicode[STIX]{x1D706}_{i}\mid \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}(i)}$
for all
$\unicode[STIX]{x1D706}_{i}\mid \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}(i)}$
for all
![]() $i=1,\ldots ,k$
. This is a partial ordering on the partitions of length
$i=1,\ldots ,k$
. This is a partial ordering on the partitions of length
![]() $k$
. We write
$k$
. We write
for the
![]() $\mathbb{Q}[q]_{(q-1)}$
-subspace of
$\mathbb{Q}[q]_{(q-1)}$
-subspace of
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
generated by clear stack functions of central type divisible by
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})_{(q-1)}$
generated by clear stack functions of central type divisible by
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
We will prove the following.
(i) The operator
 $\widetilde{I}_{k}^{\circ ,\text{ss}}$
preserves the filtration (14) by divisibility of partitions.
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
preserves the filtration (14) by divisibility of partitions.(ii) On the quotient
 $K^{{\geqslant}\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}/K^{{>}\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}$
, the operator
$K^{{\geqslant}\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}/K^{{>}\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}$
, the operator
 $\widetilde{I}_{k}^{\circ ,\text{ss}}$
acts as multiplication by
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
acts as multiplication by
 $\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}$
.
$\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}$
.(iii) The operator
 $\widetilde{I}_{k}^{\circ ,\text{ss}}$
is locally finite.
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
is locally finite.
These facts will imply the claims concerning diagonalizability of
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}$
. This is because for a lower triangular matrix with distinct diagonal entries over a discrete valuation ring to be diagonalizable, it suffices that the differences between the diagonal entries are units. The latter condition is satisfied, because if
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
. This is because for a lower triangular matrix with distinct diagonal entries over a discrete valuation ring to be diagonalizable, it suffices that the differences between the diagonal entries are units. The latter condition is satisfied, because if
![]() $\unicode[STIX]{x1D706}\mid \unicode[STIX]{x1D707}$
, then
$\unicode[STIX]{x1D706}\mid \unicode[STIX]{x1D707}$
, then
![]() $\widetilde{Q}_{\unicode[STIX]{x1D707}}-\widetilde{Q}_{\unicode[STIX]{x1D706}}$
does not vanish at
$\widetilde{Q}_{\unicode[STIX]{x1D707}}-\widetilde{Q}_{\unicode[STIX]{x1D706}}$
does not vanish at
![]() $q=1$
. (This argument does not apply directly, because our eigenvalues are not linearly ordered, but only partially. Nevertheless, the conclusion remains true in this larger generality.)
$q=1$
. (This argument does not apply directly, because our eigenvalues are not linearly ordered, but only partially. Nevertheless, the conclusion remains true in this larger generality.)
Let us fix a partition
![]() $\unicode[STIX]{x1D706}$
of length
$\unicode[STIX]{x1D706}$
of length
![]() $k$
and consider a clear stack function
$k$
and consider a clear stack function
![]() $X\rightarrow \mathfrak{M}$
of central type
$X\rightarrow \mathfrak{M}$
of central type
![]() $\unicode[STIX]{x1D706}$
with algebra
$\unicode[STIX]{x1D706}$
with algebra
![]() $A\rightarrow X$
. Abbreviate the induced element of
$A\rightarrow X$
. Abbreviate the induced element of
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
by
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
by
![]() $[X]$
. Denote the central rank of
$[X]$
. Denote the central rank of
![]() $X$
by
$X$
by
![]() $n$
, so that
$n$
, so that
![]() $\unicode[STIX]{x1D706}\vdash n$
. As
$\unicode[STIX]{x1D706}\vdash n$
. As
![]() $A$
has
$A$
has
![]() $k$
central idempotents,
$k$
central idempotents,
![]() $E_{k}X\rightarrow X$
has
$E_{k}X\rightarrow X$
has
![]() $k!$
canonical sections, each given by a labelling
$k!$
canonical sections, each given by a labelling
![]() $\unicode[STIX]{x1D70E}$
of these
$\unicode[STIX]{x1D70E}$
of these
![]() $k$
idempotents. Denote the images of these sections by
$k$
idempotents. Denote the images of these sections by
![]() $\{X_{\unicode[STIX]{x1D70E}}\}$
. By the proof of Theorem 2.5, the algebroid
$\{X_{\unicode[STIX]{x1D70E}}\}$
. By the proof of Theorem 2.5, the algebroid
![]() $E_{k}X$
can be stratified as
$E_{k}X$
can be stratified as
where the
![]() $Y_{\unicode[STIX]{x1D70F}}$
are clear algebroids of split central rank larger than
$Y_{\unicode[STIX]{x1D70F}}$
are clear algebroids of split central rank larger than
![]() $k$
. The part of
$k$
. The part of
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}X\rightarrow E_{k}X$
lying over
$\widetilde{I}_{k}^{\circ ,\text{ss}}X\rightarrow E_{k}X$
lying over
![]() $Y_{\unicode[STIX]{x1D70F}}$
then also has split central rank larger than
$Y_{\unicode[STIX]{x1D70F}}$
then also has split central rank larger than
![]() $k$
. Hence, when calculating
$k$
. Hence, when calculating
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}[X]$
, we can discard all
$\widetilde{I}_{k}^{\circ ,\text{ss}}[X]$
, we can discard all
![]() $Y_{\unicode[STIX]{x1D70F}}$
. Every
$Y_{\unicode[STIX]{x1D70F}}$
. Every
![]() $X_{\unicode[STIX]{x1D70E}}$
is isomorphic to
$X_{\unicode[STIX]{x1D70E}}$
is isomorphic to
![]() $X$
, and so we will fix a labelling
$X$
, and so we will fix a labelling
![]() $\unicode[STIX]{x1D70E}$
and replace
$\unicode[STIX]{x1D70E}$
and replace
![]() $X_{\unicode[STIX]{x1D70E}}$
by
$X_{\unicode[STIX]{x1D70E}}$
by
![]() $X$
in the following arguments, remembering to multiply the final result by
$X$
in the following arguments, remembering to multiply the final result by
![]() $k!$
.
$k!$
.
We need to consider
![]() $A^{\times ,\text{ss}}$
and its quotient
$A^{\times ,\text{ss}}$
and its quotient
![]() $\widetilde{A}^{\times ,\text{ss}}$
. We write
$\widetilde{A}^{\times ,\text{ss}}$
. We write
where
![]() $Z\subset A$
is the centre of
$Z\subset A$
is the centre of
![]() $A$
(which is a strict subbundle and hence a closed substack) and
$A$
(which is a strict subbundle and hence a closed substack) and
![]() $NZ$
is its complement. We start by examining
$NZ$
is its complement. We start by examining
![]() $Z^{\times ,\text{ss}}$
and its quotient
$Z^{\times ,\text{ss}}$
and its quotient
![]() $\widetilde{Z}^{\times ,\text{ss}}=Z^{\times ,\text{ss}}/\mathbb{G}_{m}^{k}$
. Note that
$\widetilde{Z}^{\times ,\text{ss}}=Z^{\times ,\text{ss}}/\mathbb{G}_{m}^{k}$
. Note that
![]() $Z^{\times ,\text{ss}}$
and
$Z^{\times ,\text{ss}}$
and
![]() $\widetilde{Z}^{\times ,\text{ss}}$
are pullbacks from the coarse Deligne–Mumford stack
$\widetilde{Z}^{\times ,\text{ss}}$
are pullbacks from the coarse Deligne–Mumford stack
![]() $\overline{X}$
of
$\overline{X}$
of
![]() $X$
and hence are inert over
$X$
and hence are inert over
![]() $X$
, and their algebroid structures are hence the canonical algebroid structures as inert
$X$
, and their algebroid structures are hence the canonical algebroid structures as inert
![]() $X$
-stacks.
$X$
-stacks.
Claim. In
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we have
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we have
As in the proof of Theorem 2.5, let
![]() $\widetilde{X}\rightarrow X$
be a connected Galois cover with Galois group
$\widetilde{X}\rightarrow X$
be a connected Galois cover with Galois group
![]() $\unicode[STIX]{x1D6E4}$
acting on the set
$\unicode[STIX]{x1D6E4}$
acting on the set
![]() $\text{}\underline{n}$
such that
$\text{}\underline{n}$
such that
We get induced isomorphisms
and
By Proposition 1.35, we have a surjective closed immersion
It follows that we have a surjective closed immersion
and by passing to the quotient, another surjective closed immersion
So, in
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we can replace
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we can replace
![]() $\widetilde{Z}^{\times ,\text{ss}}$
by
$\widetilde{Z}^{\times ,\text{ss}}$
by
![]() $(\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{G}_{m}^{n})/\mathbb{G}_{m}^{k}$
.
$(\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{G}_{m}^{n})/\mathbb{G}_{m}^{k}$
.
Our labelling
![]() $\unicode[STIX]{x1D70E}$
of the central idempotents in
$\unicode[STIX]{x1D70E}$
of the central idempotents in
![]() $A_{X}$
corresponds to a labelling of the orbits of
$A_{X}$
corresponds to a labelling of the orbits of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\text{}\underline{n}$
and a labelling of the parts of
$\text{}\underline{n}$
and a labelling of the parts of
![]() $\unicode[STIX]{x1D706}\vdash n$
. Let us denote these orbits by
$\unicode[STIX]{x1D706}\vdash n$
. Let us denote these orbits by
![]() $I_{1},\ldots ,I_{k}$
and
$I_{1},\ldots ,I_{k}$
and
![]() $\unicode[STIX]{x1D706}$
by
$\unicode[STIX]{x1D706}$
by
![]() $(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{k})$
such that
$(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{k})$
such that
![]() $\unicode[STIX]{x1D706}_{i}=|I_{i}|$
for
$\unicode[STIX]{x1D706}_{i}=|I_{i}|$
for
![]() $i=1,\ldots ,k$
. We write
$i=1,\ldots ,k$
. We write
![]() $\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
for the product of projective spaces
$\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
for the product of projective spaces
![]() $\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}_{1}})\times \cdots \times \mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}_{k}})$
. Moreover, for a sequence of subsets
$\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}_{1}})\times \cdots \times \mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}_{k}})$
. Moreover, for a sequence of subsets
![]() $J_{i}\subset I_{i}$
, we write
$J_{i}\subset I_{i}$
, we write
![]() $\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})\subset \mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
for the locally closed subspace defined by the entries in
$\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})\subset \mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
for the locally closed subspace defined by the entries in
![]() $J_{1}\cup \cdots \cup J_{k}$
being non-zero and all others being zero. We have
$J_{1}\cup \cdots \cup J_{k}$
being non-zero and all others being zero. We have
where the disjoint union is over all sequences of subsets
![]() $J_{i}\subset I_{i}$
.
$J_{i}\subset I_{i}$
.
The group
![]() $\unicode[STIX]{x1D6E4}$
acts linearly on
$\unicode[STIX]{x1D6E4}$
acts linearly on
![]() $\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
, respecting this stratification (although not the individual strata), and we have
$\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
, respecting this stratification (although not the individual strata), and we have
Moreover,

Every subgroup
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subsetneq \unicode[STIX]{x1D6E4}$
that is the stabilizer of a sequence
$\unicode[STIX]{x1D6E4}^{\prime }\subsetneq \unicode[STIX]{x1D6E4}$
that is the stabilizer of a sequence
![]() $(J_{1},\ldots ,J_{k})$
has more than
$(J_{1},\ldots ,J_{k})$
has more than
![]() $k$
orbits on
$k$
orbits on
![]() $\text{}\underline{n}$
. As in the proof of Theorem 2.5, this implies that
$\text{}\underline{n}$
. As in the proof of Theorem 2.5, this implies that
![]() $\widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is in
$\widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is in
![]() $K^{{>}k}(\mathfrak{M})$
. The same is then true for
$K^{{>}k}(\mathfrak{M})$
. The same is then true for
![]() $\widetilde{X}\times _{\unicode[STIX]{x1D6E4}^{\prime }}\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})$
, as the projection
$\widetilde{X}\times _{\unicode[STIX]{x1D6E4}^{\prime }}\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})$
, as the projection
![]() $\widetilde{X}\times _{\unicode[STIX]{x1D6E4}^{\prime }}\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})\rightarrow \widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is inert (being the pullback of a corresponding morphism of course Deligne–Mumford stacks). We deduce that in
$\widetilde{X}\times _{\unicode[STIX]{x1D6E4}^{\prime }}\mathbb{P}^{\ast }(J_{1},\ldots ,J_{k})\rightarrow \widetilde{X}/\unicode[STIX]{x1D6E4}^{\prime }$
is inert (being the pullback of a corresponding morphism of course Deligne–Mumford stacks). We deduce that in
![]() $K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we have
$K^{{\geqslant}k}/K^{{>}k}(\mathfrak{M})$
, we have
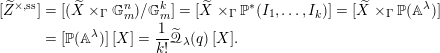 $$\begin{eqnarray}\displaystyle [\widetilde{Z}^{\times ,\text{ss}}] & = & \displaystyle [(\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{G}_{m}^{n})/\mathbb{G}_{m}^{k}]=[\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}^{\ast }(I_{1},\ldots ,I_{k})]=[\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})]\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})]\,[X]=\frac{1}{k!}\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}(q)\,[X].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\widetilde{Z}^{\times ,\text{ss}}] & = & \displaystyle [(\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{G}_{m}^{n})/\mathbb{G}_{m}^{k}]=[\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}^{\ast }(I_{1},\ldots ,I_{k})]=[\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})]\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})]\,[X]=\frac{1}{k!}\widetilde{\mathscr{Q}}_{\unicode[STIX]{x1D706}}(q)\,[X].\end{eqnarray}$$
In the last step, we used the bundle relations in
![]() $K(\mathfrak{M})$
. The bundle
$K(\mathfrak{M})$
. The bundle
![]() $\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
is a product of projective bundles associated to vector bundles, whose structure groups are special (as they are general linear groups). This finishes the proof of this claim.
$\widetilde{X}\times _{\unicode[STIX]{x1D6E4}}\mathbb{P}(\mathbb{A}^{\unicode[STIX]{x1D706}})$
is a product of projective bundles associated to vector bundles, whose structure groups are special (as they are general linear groups). This finishes the proof of this claim.
Now consider a locally closed embedding
![]() $Y{\hookrightarrow}NZ^{\times ,ss}/\mathbb{G}_{m}^{k}$
such that
$Y{\hookrightarrow}NZ^{\times ,ss}/\mathbb{G}_{m}^{k}$
such that
![]() $Y$
is a clear algebroid.
$Y$
is a clear algebroid.
Claim. The central type of
![]() $Y$
strictly divides
$Y$
strictly divides
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
Over
![]() $Y$
, we then consider the inclusion of commutative algebra bundles
$Y$
, we then consider the inclusion of commutative algebra bundles
![]() $ZA_{X}|_{Y}{\hookrightarrow}ZA_{Y}$
. By Proposition 1.36, the split rank of
$ZA_{X}|_{Y}{\hookrightarrow}ZA_{Y}$
. By Proposition 1.36, the split rank of
![]() $ZA_{Y}$
(which is the split central rank of
$ZA_{Y}$
(which is the split central rank of
![]() $Y$
) is at least as large as the split rank of
$Y$
) is at least as large as the split rank of
![]() $ZA_{X}|_{Y}$
, which, in turn, is at least as large as the split rank of
$ZA_{X}|_{Y}$
, which, in turn, is at least as large as the split rank of
![]() $ZA_{X}$
, which is
$ZA_{X}$
, which is
![]() $k$
. Since we are working modulo
$k$
. Since we are working modulo
![]() $K^{{>}k}(\mathfrak{M})$
, we may assume that the split central rank of
$K^{{>}k}(\mathfrak{M})$
, we may assume that the split central rank of
![]() $Y$
is
$Y$
is
![]() $k$
and hence that the split rank of
$k$
and hence that the split rank of
![]() $ZA_{Y}$
and of
$ZA_{Y}$
and of
![]() $ZA_{X}|_{Y}$
are both equal to
$ZA_{X}|_{Y}$
are both equal to
![]() $k$
. Consider the correspondence
$k$
. Consider the correspondence
![]() $Q$
which we used in the proof of Proposition 1.36:
$Q$
which we used in the proof of Proposition 1.36:

All three stacks in this diagram are representable finite étale covers of
![]() $Y$
. By assumption, both
$Y$
. By assumption, both
![]() $PZE(A_{Y})$
and
$PZE(A_{Y})$
and
![]() $PZE(A_{X}|_{Y})$
have
$PZE(A_{X}|_{Y})$
have
![]() $k$
connected components. This implies that the horizontal inclusion in the diagram is an isomorphism and that we have a surjective representable finite étale cover
$k$
connected components. This implies that the horizontal inclusion in the diagram is an isomorphism and that we have a surjective representable finite étale cover
Since
![]() $PZE(A_{X}|_{Y})$
and
$PZE(A_{X}|_{Y})$
and
![]() $PZE(A_{X})$
have the same number of components, the degrees of these components are equal as well, which means that the central type of
$PZE(A_{X})$
have the same number of components, the degrees of these components are equal as well, which means that the central type of
![]() $A_{X}|_{Y}$
is equal to the central type of
$A_{X}|_{Y}$
is equal to the central type of
![]() $A_{X}$
, which is
$A_{X}$
, which is
![]() $\unicode[STIX]{x1D706}$
. The existence of (17) then implies that
$\unicode[STIX]{x1D706}$
. The existence of (17) then implies that
![]() $\unicode[STIX]{x1D706}$
divides the central type of
$\unicode[STIX]{x1D706}$
divides the central type of
![]() $A_{Y}$
.
$A_{Y}$
.
The surjection (17) is not an isomorphism, because otherwise, by Proposition 1.36, we would have a surjection
![]() $ZA_{Y}^{\times ,\text{ss}}\rightarrow ZA_{X}^{\times ,\text{ss}}|_{Y}$
; but this would force the tautological section class of
$ZA_{Y}^{\times ,\text{ss}}\rightarrow ZA_{X}^{\times ,\text{ss}}|_{Y}$
; but this would force the tautological section class of
![]() $ZA_{Y}^{\times ,\text{ss}}$
, given by the structure map
$ZA_{Y}^{\times ,\text{ss}}$
, given by the structure map
![]() $Y\rightarrow A_{X}^{\times ,\text{ss}}/\mathbb{G}_{m}^{k}$
, to be central in
$Y\rightarrow A_{X}^{\times ,\text{ss}}/\mathbb{G}_{m}^{k}$
, to be central in
![]() $A_{X}$
(at least pointwise), which it is not.
$A_{X}$
(at least pointwise), which it is not.
This shows that the central type of
![]() $Y$
strictly divides
$Y$
strictly divides
![]() $\unicode[STIX]{x1D706}$
and proves our second claim.
$\unicode[STIX]{x1D706}$
and proves our second claim.
We have thus completed the proof of (i) and (ii). For the local finiteness of
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}$
, we proceed as in the proof of Corollary 2.6. Every time we apply
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
, we proceed as in the proof of Corollary 2.6. Every time we apply
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}$
, we produce only clear algebroids whose central type is a multiple of
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
, we produce only clear algebroids whose central type is a multiple of
![]() $\unicode[STIX]{x1D706}$
, but as we can bound the central rank by the rank, which does not increase by applying
$\unicode[STIX]{x1D706}$
, but as we can bound the central rank by the rank, which does not increase by applying
![]() $\widetilde{I}_{k}^{\circ ,\text{ss}}$
, after finitely many steps, this process stops.◻
$\widetilde{I}_{k}^{\circ ,\text{ss}}$
, after finitely many steps, this process stops.◻
Corollary 2.17. The operator
![]() $I^{\circ ,\text{ss}}:K(\mathfrak{M})_{(q-1)}\rightarrow K(\mathfrak{M})_{(q-1)}$
is diagonalizable. Its eigenvalue spectrum consists of the
$I^{\circ ,\text{ss}}:K(\mathfrak{M})_{(q-1)}\rightarrow K(\mathfrak{M})_{(q-1)}$
is diagonalizable. Its eigenvalue spectrum consists of the
![]() $\mathscr{Q}_{\unicode[STIX]{x1D706}}\in \mathbb{Q}[q]$
, for all partitions
$\mathscr{Q}_{\unicode[STIX]{x1D706}}\in \mathbb{Q}[q]$
, for all partitions
![]() $\unicode[STIX]{x1D706}$
. Denote the eigenspace corresponding to the eigenvalue
$\unicode[STIX]{x1D706}$
. Denote the eigenspace corresponding to the eigenvalue
![]() $\mathscr{Q}_{\unicode[STIX]{x1D706}}$
by
$\mathscr{Q}_{\unicode[STIX]{x1D706}}$
by
![]() $K^{\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}$
. We have
$K^{\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}$
. We have
Example 2.18. Consider, as in Example 2.13, the stack function of rank 2 vector bundles. It defines an element
![]() $[B\operatorname{GL}_{2}]$
of
$[B\operatorname{GL}_{2}]$
of
![]() $K^{{\geqslant}1}/K^{{>}1}(\mathfrak{Vect})$
, which we are going to decompose into its eigencomponents with respect to the operator
$K^{{\geqslant}1}/K^{{>}1}(\mathfrak{Vect})$
, which we are going to decompose into its eigencomponents with respect to the operator
![]() $\widetilde{I}_{1}^{\circ ,\text{ss}}$
.
$\widetilde{I}_{1}^{\circ ,\text{ss}}$
.
The stack function
![]() $[B\operatorname{GL}_{2}]$
is clear; its central rank is 1. The decomposition (15) is given in this case as
$[B\operatorname{GL}_{2}]$
is clear; its central rank is 1. The decomposition (15) is given in this case as
where
![]() $\unicode[STIX]{x1D6E5}$
is the central torus of
$\unicode[STIX]{x1D6E5}$
is the central torus of
![]() $\operatorname{GL}_{2}$
and
$\operatorname{GL}_{2}$
and
![]() $T^{\ast }=T\setminus \unicode[STIX]{x1D6E5}$
. Also,
$T^{\ast }=T\setminus \unicode[STIX]{x1D6E5}$
. Also,
![]() $N$
is the normalizer of
$N$
is the normalizer of
![]() $T$
in
$T$
in
![]() $\operatorname{GL}_{2}$
. We get the corresponding decomposition
$\operatorname{GL}_{2}$
. We get the corresponding decomposition
where
![]() $\widetilde{T}^{\ast }=T^{\ast }/\mathbb{G}_{m}$
, and we have
$\widetilde{T}^{\ast }=T^{\ast }/\mathbb{G}_{m}$
, and we have
Note that
![]() $\widetilde{T}^{\ast }/N$
is not a strict algebroid. In fact, let
$\widetilde{T}^{\ast }/N$
is not a strict algebroid. In fact, let
![]() $T^{\prime }\subset T^{\ast }$
be the closed subscheme consisting of elements of trace zero and write
$T^{\prime }\subset T^{\ast }$
be the closed subscheme consisting of elements of trace zero and write
![]() $T^{\ast }=T^{\prime }\sqcup \,T^{\ast \ast }$
. Then (at least if
$T^{\ast }=T^{\prime }\sqcup \,T^{\ast \ast }$
. Then (at least if
![]() $2\in R^{\times }$
) we have
$2\in R^{\times }$
) we have
![]() $T^{\prime }/\mathbb{G}_{m}=\operatorname{Spec}R$
, and
$T^{\prime }/\mathbb{G}_{m}=\operatorname{Spec}R$
, and
![]() $[\widetilde{T}^{\ast }/N]=[BN]+[\widetilde{T}^{\ast \ast }/N]$
, and
$[\widetilde{T}^{\ast }/N]=[BN]+[\widetilde{T}^{\ast \ast }/N]$
, and
![]() $BN$
is not a strict algebroid, as
$BN$
is not a strict algebroid, as
![]() $N$
is not connected. But
$N$
is not connected. But
![]() $\widetilde{T}^{\ast }/N$
is a clear algebroid. Its connected inertia stack is
$\widetilde{T}^{\ast }/N$
is a clear algebroid. Its connected inertia stack is
![]() $\widetilde{T}^{\ast }\times T/N$
, and its associated coarse Deligne–Mumford stack is
$\widetilde{T}^{\ast }\times T/N$
, and its associated coarse Deligne–Mumford stack is
![]() $\widetilde{T}^{\ast }/\mathbb{Z}_{2}$
, which is only generically a scheme. The central rank of
$\widetilde{T}^{\ast }/\mathbb{Z}_{2}$
, which is only generically a scheme. The central rank of
![]() $\widetilde{T}^{\ast }/N$
is 2, and the split central rank 1.
$\widetilde{T}^{\ast }/N$
is 2, and the split central rank 1.
Now we consider
![]() $\widetilde{I}_{1}^{\circ ,\text{ss}}[\widetilde{T}^{\ast }/N]$
. We start by noting that all connected inertia of
$\widetilde{I}_{1}^{\circ ,\text{ss}}[\widetilde{T}^{\ast }/N]$
. We start by noting that all connected inertia of
![]() $\widetilde{T}^{\ast }/N$
is central. Hence, modulo
$\widetilde{T}^{\ast }/N$
is central. Hence, modulo
![]() $K^{{>}1}(\mathfrak{Vect})$
, we have
$K^{{>}1}(\mathfrak{Vect})$
, we have
by (16).
We see that
![]() $\mathbb{Q}[q]_{(q-1)}[B\operatorname{GL}_{2}]+\mathbb{Q}[q]_{(q-1)}[\widetilde{T}^{\ast }/N]$
is invariant under
$\mathbb{Q}[q]_{(q-1)}[B\operatorname{GL}_{2}]+\mathbb{Q}[q]_{(q-1)}[\widetilde{T}^{\ast }/N]$
is invariant under
![]() $\widetilde{I}_{1}^{\circ ,\text{ss}}$
, and the matrix of
$\widetilde{I}_{1}^{\circ ,\text{ss}}$
, and the matrix of
![]() $\widetilde{I}_{1}^{\circ ,\text{ss}}$
on this subspace is
$\widetilde{I}_{1}^{\circ ,\text{ss}}$
on this subspace is
This matrix is lower triangular, and the differences between the scalars on the diagonal are all invertible in
![]() $\mathbb{Q}[q]_{(q-1)}$
. Therefore, it is diagonalizable over
$\mathbb{Q}[q]_{(q-1)}$
. Therefore, it is diagonalizable over
![]() $\mathbb{Q}[q]_{(q-1)}$
. Diagonalizing, we get the following eigenvectors modulo
$\mathbb{Q}[q]_{(q-1)}$
. Diagonalizing, we get the following eigenvectors modulo
![]() $K^{{>}1}(\mathfrak{Vect})_{(q-1)}$
:
$K^{{>}1}(\mathfrak{Vect})_{(q-1)}$
:
(i)
 $\overline{v}_{(1)}=[B\operatorname{GL}_{2}]-(1/q)[\widetilde{T}^{\ast }/N]$
;
$\overline{v}_{(1)}=[B\operatorname{GL}_{2}]-(1/q)[\widetilde{T}^{\ast }/N]$
;(ii)
 $\overline{v}_{(2)}=(1/q)[\widetilde{T}^{\ast }/N]$
.
$\overline{v}_{(2)}=(1/q)[\widetilde{T}^{\ast }/N]$
.
To get the actual eigenvectors, we project into
![]() $K^{1}(\mathfrak{Vect})_{(q-1)}$
. We have:
$K^{1}(\mathfrak{Vect})_{(q-1)}$
. We have:
(i)
 $\unicode[STIX]{x1D70B}_{1}[B\operatorname{GL}_{2}]=[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
;
$\unicode[STIX]{x1D70B}_{1}[B\operatorname{GL}_{2}]=[B\operatorname{GL}_{2}]-\frac{1}{2}[BT]$
;(ii)
 $\unicode[STIX]{x1D70B}_{1}[\widetilde{T}^{\ast }/N]=[\widetilde{T}^{\ast }/N]-\frac{1}{2}(q-2)[BT]$
$\unicode[STIX]{x1D70B}_{1}[\widetilde{T}^{\ast }/N]=[\widetilde{T}^{\ast }/N]-\frac{1}{2}(q-2)[BT]$
and hence
(i)
 $v_{(1)}=[B\operatorname{GL}_{2}]-(1/q)[\widetilde{T}^{\ast }/N]-(1/q)[BT]$
;
$v_{(1)}=[B\operatorname{GL}_{2}]-(1/q)[\widetilde{T}^{\ast }/N]-(1/q)[BT]$
;(ii)
 $v_{(2)}=(1/q)[\widetilde{T}^{\ast }/N]-((q-2)/2q)[BT]$
.
$v_{(2)}=(1/q)[\widetilde{T}^{\ast }/N]-((q-2)/2q)[BT]$
.
If we add
(iii)
 $v_{(1,1)}=\frac{1}{2}[B\operatorname{GL}_{2}]$
$v_{(1,1)}=\frac{1}{2}[B\operatorname{GL}_{2}]$
we get the spectral decomposition
![]() $[B\operatorname{GL}_{2}]=v_{(1)}+v_{(2)}+v_{(1,1)}$
of
$[B\operatorname{GL}_{2}]=v_{(1)}+v_{(2)}+v_{(1,1)}$
of
![]() $[B\operatorname{GL}_{2}]$
, with respect to the operator
$[B\operatorname{GL}_{2}]$
, with respect to the operator
![]() $I^{\circ ,\text{ss}}$
. This is, of course, the same as the spectral decomposition with respect to
$I^{\circ ,\text{ss}}$
. This is, of course, the same as the spectral decomposition with respect to
![]() $I^{\text{ss}}$
, which we computed in the introduction (after applying the bundle relations).
$I^{\text{ss}}$
, which we computed in the introduction (after applying the bundle relations).
Remark 2.19. If we are willing to invert
![]() $(q-1)$
, we can prove the diagonalizability of
$(q-1)$
, we can prove the diagonalizability of
![]() $I^{\circ ,\text{ss}}=I^{\text{ss}}$
entirely within the context of strict algebroids. In fact, we can generalize the calculation in the introduction to accomplish this.
$I^{\circ ,\text{ss}}=I^{\text{ss}}$
entirely within the context of strict algebroids. In fact, we can generalize the calculation in the introduction to accomplish this.
2.3 Graded structure of multiplication
We will now assume that
![]() $\mathfrak{M}$
admits all direct sums. Then we can define a commutative product on
$\mathfrak{M}$
admits all direct sums. Then we can define a commutative product on
![]() $K(\mathfrak{M})$
by
$K(\mathfrak{M})$
by
With this product,
![]() $K(\mathfrak{M})$
becomes a commutative
$K(\mathfrak{M})$
becomes a commutative
![]() $K(\text{DM})$
-algebra with unit
$K(\text{DM})$
-algebra with unit
![]() $1=[\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
.
$1=[\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}]$
.
Proposition 2.20. For
![]() $x,y\in K(\mathfrak{M})$
, we have
$x,y\in K(\mathfrak{M})$
, we have
Proof. This follows immediately from the fact that, for any two algebroids
![]() $X$
,
$X$
,
![]() $Y$
, we have
$Y$
, we have
![]() $A_{X\times Y}^{\times ,\text{ss}}=A_{X}^{\times ,\text{ss}}\times A_{Y}^{\times ,\text{ss}}$
as algebroids over
$A_{X\times Y}^{\times ,\text{ss}}=A_{X}^{\times ,\text{ss}}\times A_{Y}^{\times ,\text{ss}}$
as algebroids over
![]() $X\times Y$
.◻
$X\times Y$
.◻
Denote the disjoint union of two partitions
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
by
$\unicode[STIX]{x1D707}$
by
![]() $\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}$
.
Corollary 2.21. We have
![]() $K^{\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}\cdot K^{\unicode[STIX]{x1D707}}(\mathfrak{M})_{(q-1)}\subset K^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}(\mathfrak{M})_{(q-1)}$
and therefore also
$K^{\unicode[STIX]{x1D706}}(\mathfrak{M})_{(q-1)}\cdot K^{\unicode[STIX]{x1D707}}(\mathfrak{M})_{(q-1)}\subset K^{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707}}(\mathfrak{M})_{(q-1)}$
and therefore also
![]() $K^{k}(\mathfrak{M})_{(q-1)}\cdot K^{\ell }(\mathfrak{M})_{(q-1)}\subset K^{k+\ell }(\mathfrak{M})_{(q-1)}$
.
$K^{k}(\mathfrak{M})_{(q-1)}\cdot K^{\ell }(\mathfrak{M})_{(q-1)}\subset K^{k+\ell }(\mathfrak{M})_{(q-1)}$
.
So the
![]() $\mathbb{Q}[q]_{(q-1)}$
-module
$\mathbb{Q}[q]_{(q-1)}$
-module
is a graded
![]() $\mathbb{Q}[q]_{(q-1)}$
-algebra with respect to the commutative product on
$\mathbb{Q}[q]_{(q-1)}$
-algebra with respect to the commutative product on
![]() $K(\mathfrak{M})_{(q-1)}$
. We will prove next that this fact is true for
$K(\mathfrak{M})_{(q-1)}$
. We will prove next that this fact is true for
![]() $K(\mathfrak{M})$
itself.
$K(\mathfrak{M})$
itself.
Proposition 2.22. For any
![]() $x,y\in K(\mathfrak{M})$
and any
$x,y\in K(\mathfrak{M})$
and any
![]() $p\geqslant 0$
, we have
$p\geqslant 0$
, we have
Here ![]() is the number of ways the set
is the number of ways the set
![]() $\text{}\underline{p}$
can bewritten as the union of a subset of order
$\text{}\underline{p}$
can bewritten as the union of a subset of order
![]() $n$
and a subset of order
$n$
and a subset of order
![]() $m$
.
$m$
.
Proof. Consider stack functions
![]() $X\rightarrow \mathfrak{M}$
and
$X\rightarrow \mathfrak{M}$
and
![]() $Y\rightarrow \mathfrak{M}$
. Then
$Y\rightarrow \mathfrak{M}$
. Then
![]() $E_{p}(X\times Y)$
is the stack of pairs
$E_{p}(X\times Y)$
is the stack of pairs
![]() $(e,f)$
, where
$(e,f)$
, where
![]() $e=(e_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of orthogonal idempotents in
$e=(e_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of orthogonal idempotents in
![]() $A_{X}$
and
$A_{X}$
and
![]() $f=(f_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of orthogonal idempotents in
$f=(f_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of orthogonal idempotents in
![]() $A_{Y}$
such that for every
$A_{Y}$
such that for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of the two idempotents
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of the two idempotents
![]() $e_{\unicode[STIX]{x1D70C}}$
,
$e_{\unicode[STIX]{x1D70C}}$
,
![]() $f_{\unicode[STIX]{x1D70C}}$
is non-zero.
$f_{\unicode[STIX]{x1D70C}}$
is non-zero.
For every pair of strictly monotone maps
![]() $\text{}\underline{n}{\hookrightarrow}\text{}\underline{p}$
,
$\text{}\underline{n}{\hookrightarrow}\text{}\underline{p}$
,
![]() $\text{}\underline{m}{\hookrightarrow}\text{}\underline{p}$
whose images cover
$\text{}\underline{m}{\hookrightarrow}\text{}\underline{p}$
whose images cover
![]() $\text{}\underline{p}$
, we get a morphism of stack functions
$\text{}\underline{p}$
, we get a morphism of stack functions
![]() $E_{n}(X)\times E_{m}(Y)\rightarrow E_{p}(X\times Y)$
by mapping a pair of complete sets of orthogonal idempotents
$E_{n}(X)\times E_{m}(Y)\rightarrow E_{p}(X\times Y)$
by mapping a pair of complete sets of orthogonal idempotents
![]() $(e^{\prime },f^{\prime })$
, where
$(e^{\prime },f^{\prime })$
, where
![]() $e^{\prime }=(e_{\unicode[STIX]{x1D708}}^{\prime })_{\unicode[STIX]{x1D708}\in \text{}\underline{n}}$
and
$e^{\prime }=(e_{\unicode[STIX]{x1D708}}^{\prime })_{\unicode[STIX]{x1D708}\in \text{}\underline{n}}$
and
![]() $f^{\prime }=(f_{\unicode[STIX]{x1D707}}^{\prime })_{\unicode[STIX]{x1D707}\in \text{}\underline{m}}$
, to the pair
$f^{\prime }=(f_{\unicode[STIX]{x1D707}}^{\prime })_{\unicode[STIX]{x1D707}\in \text{}\underline{m}}$
, to the pair
![]() $(e,f)$
, defined by
$(e,f)$
, defined by
(As the maps
![]() $\text{}\underline{n}\rightarrow \text{}\underline{p}$
and
$\text{}\underline{n}\rightarrow \text{}\underline{p}$
and
![]() $\text{}\underline{m}\rightarrow \text{}\underline{p}$
are injective, all these sums have either zero or one summand.)
$\text{}\underline{m}\rightarrow \text{}\underline{p}$
are injective, all these sums have either zero or one summand.)
Each of the morphisms
![]() $E_{n}(X)\times E_{m}(X)\rightarrow E_{p}(X\times Y)$
is an isomorphism onto a locally closed substack, because the locus of vanishing for an idempotent is closed. Moreover, the images of these morphisms are disjoint and from a cover. There are
$E_{n}(X)\times E_{m}(X)\rightarrow E_{p}(X\times Y)$
is an isomorphism onto a locally closed substack, because the locus of vanishing for an idempotent is closed. Moreover, the images of these morphisms are disjoint and from a cover. There are ![]() of them.◻
of them.◻
Corollary 2.23. If
![]() $x\in K^{k}(\mathfrak{M})$
and
$x\in K^{k}(\mathfrak{M})$
and
![]() $y\in K^{\ell }(\mathfrak{M})$
, then
$y\in K^{\ell }(\mathfrak{M})$
, then
![]() $x\cdot y\in K^{k+\ell }(\mathfrak{M})$
.
$x\cdot y\in K^{k+\ell }(\mathfrak{M})$
.
Proof. We have
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70B}_{t}(x\cdot y) & = & \displaystyle \displaystyle \mathop{\sum }_{p}\binom{t}{p}E_{p}(x\cdot y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{p}\binom{t}{p}\mathop{\sum }_{n,m}\left[\binom{p}{n,m}\right]E_{n}(x)\cdot E_{m}(y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n,m}\biggl(\mathop{\sum }_{p}\left[\binom{p}{n,m}\right]\binom{t}{p}\biggr)E_{n}(x)\cdot E_{m}(y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n,m}\binom{t}{n}\binom{t}{m}E_{n}(x)\cdot E_{m}(x)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \unicode[STIX]{x1D70B}_{t}(x)\cdot \unicode[STIX]{x1D70B}_{t}(y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D70B}_{t}(x\cdot y) & = & \displaystyle \displaystyle \mathop{\sum }_{p}\binom{t}{p}E_{p}(x\cdot y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{p}\binom{t}{p}\mathop{\sum }_{n,m}\left[\binom{p}{n,m}\right]E_{n}(x)\cdot E_{m}(y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n,m}\biggl(\mathop{\sum }_{p}\left[\binom{p}{n,m}\right]\binom{t}{p}\biggr)E_{n}(x)\cdot E_{m}(y)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n,m}\binom{t}{n}\binom{t}{m}E_{n}(x)\cdot E_{m}(x)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \unicode[STIX]{x1D70B}_{t}(x)\cdot \unicode[STIX]{x1D70B}_{t}(y).\nonumber\end{eqnarray}$$
The step from line 3 to line 4 uses Proposition 2.24, below. ◻
A combinatorial lemma
Let
![]() $p\geqslant 0$
.
$p\geqslant 0$
.
For a non-negative integer
![]() $n$
and a
$n$
and a
![]() $p$
-tuple of non-negative integers
$p$
-tuple of non-negative integers
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p})$
, we define
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p})$
, we define
to be the number of indexed covers of
![]() $\text{}\underline{n}$
by subsets
$\text{}\underline{n}$
by subsets
![]() $S_{1},\ldots ,S_{p}$
of cardinalities
$S_{1},\ldots ,S_{p}$
of cardinalities
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}$
. The non-negative integer
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}$
. The non-negative integer ![]() vanishes, unless
vanishes, unless
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}\leqslant n$
, for all
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}\leqslant n$
, for all
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
and
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
and
![]() $n\leqslant |\unicode[STIX]{x1D706}|$
, where
$n\leqslant |\unicode[STIX]{x1D706}|$
, where
![]() $|\unicode[STIX]{x1D706}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$
.
$|\unicode[STIX]{x1D706}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D70C}}$
.
We could not find the following combinatorial property in the literature.
Proposition 2.24. For every
![]() $p$
-tuple of non-negative integers
$p$
-tuple of non-negative integers
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p})$
, we have
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p})$
, we have
Proof. Let
![]() $x_{1},\ldots ,x_{p}$
be formal variables. We will prove that
$x_{1},\ldots ,x_{p}$
be formal variables. We will prove that
by proving that both sides of this equation are equal to
On the one hand, we have
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{p}(1+x_{i})^{t} & = & \displaystyle \mathop{\prod }_{i=1}^{p}\mathop{\sum }_{n}\binom{t}{n}x_{i}^{n}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\binom{t}{\unicode[STIX]{x1D706}_{1}}\ldots \binom{t}{\unicode[STIX]{x1D706}_{p}}x_{1}^{\unicode[STIX]{x1D706}_{1}}\ldots x_{p}^{\unicode[STIX]{x1D706}_{p}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{i=1}^{p}(1+x_{i})^{t} & = & \displaystyle \mathop{\prod }_{i=1}^{p}\mathop{\sum }_{n}\binom{t}{n}x_{i}^{n}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\binom{t}{\unicode[STIX]{x1D706}_{1}}\ldots \binom{t}{\unicode[STIX]{x1D706}_{p}}x_{1}^{\unicode[STIX]{x1D706}_{1}}\ldots x_{p}^{\unicode[STIX]{x1D706}_{p}}.\nonumber\end{eqnarray}$$
On the other hand, we have
 $$\begin{eqnarray}\displaystyle \displaystyle \mathop{\prod }_{i=1}^{p}(1+x_{i})^{t} & = & \displaystyle \displaystyle \biggl(1+\mathop{\prod }_{i=1}^{p}(1+x_{i})-1\biggr)^{t}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\biggl(\mathop{\prod }_{i=1}^{p}(1+x_{i})-1\biggr)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\prod }_{i=1}^{p}(1+x_{i})^{n-j}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\prod }_{i=1}^{p}\mathop{\sum }_{\ell }\binom{n-j}{\ell }x_{i}^{\ell }\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\sum }_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\binom{n-j}{\unicode[STIX]{x1D706}_{i}}x_{1}^{\unicode[STIX]{x1D706}_{1}}\ldots x_{p}^{\unicode[STIX]{x1D706}_{p}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{\unicode[STIX]{x1D706}}\biggl(\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\binom{n-j}{\unicode[STIX]{x1D706}_{i}}\biggr)x^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{\unicode[STIX]{x1D706}}\left[\binom{n}{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\right]x^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}}\mathop{\sum }_{n}\left[\binom{n}{\unicode[STIX]{x1D706}}\right]\binom{t}{n}x^{\unicode[STIX]{x1D706}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \mathop{\prod }_{i=1}^{p}(1+x_{i})^{t} & = & \displaystyle \displaystyle \biggl(1+\mathop{\prod }_{i=1}^{p}(1+x_{i})-1\biggr)^{t}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\biggl(\mathop{\prod }_{i=1}^{p}(1+x_{i})-1\biggr)^{n}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\prod }_{i=1}^{p}(1+x_{i})^{n-j}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\prod }_{i=1}^{p}\mathop{\sum }_{\ell }\binom{n-j}{\ell }x_{i}^{\ell }\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\mathop{\sum }_{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\binom{n-j}{\unicode[STIX]{x1D706}_{i}}x_{1}^{\unicode[STIX]{x1D706}_{1}}\ldots x_{p}^{\unicode[STIX]{x1D706}_{p}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{\unicode[STIX]{x1D706}}\biggl(\mathop{\sum }_{j}(-1)^{j}\binom{n}{j}\binom{n-j}{\unicode[STIX]{x1D706}_{i}}\biggr)x^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{n}\binom{t}{n}\mathop{\sum }_{\unicode[STIX]{x1D706}}\left[\binom{n}{\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{p}}\right]x^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}}\mathop{\sum }_{n}\left[\binom{n}{\unicode[STIX]{x1D706}}\right]\binom{t}{n}x^{\unicode[STIX]{x1D706}}.\nonumber\end{eqnarray}$$
Here we have used the obvious inclusion–exclusion property satisfied by the covering numbers. ◻
3 The order filtration
The Hall algebra
Let
![]() $\mathfrak{M}$
be a linear algebraic stack admitting direct sums and direct summands, i.e., assume that
$\mathfrak{M}$
be a linear algebraic stack admitting direct sums and direct summands, i.e., assume that
![]() $\mathfrak{M}$
is Karoubian (Remark 1.63). To define the Hall product, we need an additional structure on
$\mathfrak{M}$
is Karoubian (Remark 1.63). To define the Hall product, we need an additional structure on
![]() $\mathfrak{M}$
. This is a linear algebraic substack
$\mathfrak{M}$
. This is a linear algebraic substack
![]() $\mathfrak{M}^{(2)}$
of the stack of all sequences
$\mathfrak{M}^{(2)}$
of the stack of all sequences
![]() $M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
in
$M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
in
![]() $\mathfrak{M}$
such that for every
$\mathfrak{M}$
such that for every
![]() $R$
-scheme
$R$
-scheme
![]() $S$
, the fibre
$S$
, the fibre
![]() $\mathfrak{M}^{(2)}(S)$
defines the structure of an exact category on
$\mathfrak{M}^{(2)}(S)$
defines the structure of an exact category on
![]() $\mathfrak{M}(S)$
. The stack
$\mathfrak{M}(S)$
. The stack
![]() $\mathfrak{M}^{(2)}$
comes with a diagram of morphisms of linear algebraic stacks
$\mathfrak{M}^{(2)}$
comes with a diagram of morphisms of linear algebraic stacks

where
![]() $a_{1},a_{2},b:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}$
are the projections of the sequence
$a_{1},a_{2},b:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}$
are the projections of the sequence
![]() $M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
onto the objects
$M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
onto the objects
![]() $M^{\prime },M^{\prime \prime },M$
, respectively. We require further that the morphism
$M^{\prime },M^{\prime \prime },M$
, respectively. We require further that the morphism
![]() $a_{1}\times a_{2}:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}\times \mathfrak{M}$
is of finite type. Note that the morphism
$a_{1}\times a_{2}:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}\times \mathfrak{M}$
is of finite type. Note that the morphism
![]() $b:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}$
is a representable morphism of algebroids, by the properties of exact categories.
$b:\mathfrak{M}^{(2)}\rightarrow \mathfrak{M}$
is a representable morphism of algebroids, by the properties of exact categories.
We call such an
![]() $\mathfrak{M}$
an exact linear algebraic stack.
$\mathfrak{M}$
an exact linear algebraic stack.
Example 3.1. The linear stacks
![]() $\mathfrak{Coh}_{X}$
,
$\mathfrak{Coh}_{X}$
,
![]() $\mathfrak{Vect}$
, and
$\mathfrak{Vect}$
, and
![]() $\mathfrak{Rep}_{Q}$
of Examples 1.11, 1.12, and 1.13 satisfy these axioms. For
$\mathfrak{Rep}_{Q}$
of Examples 1.11, 1.12, and 1.13 satisfy these axioms. For
![]() $\mathfrak{Coh}_{X}$
, see [Reference BridgelandBri12, §4.1].
$\mathfrak{Coh}_{X}$
, see [Reference BridgelandBri12, §4.1].
In each case, the exact structure is given by all short exact sequences. Note that the categories
![]() $\mathfrak{M}(S)$
are not abelian, as the cokernel of a homomorphisms of flat sheaves is not necessarily flat.
$\mathfrak{M}(S)$
are not abelian, as the cokernel of a homomorphisms of flat sheaves is not necessarily flat.
Throughout the following discussion, we fix an exact linear algebraic stack
![]() $\mathfrak{M}$
and let
$\mathfrak{M}$
and let
![]() $\mathfrak{A}\rightarrow \mathfrak{M}$
be its universal endomorphism algebra, as in § 2.
$\mathfrak{A}\rightarrow \mathfrak{M}$
be its universal endomorphism algebra, as in § 2.
We have the following structures on
![]() $K(\mathfrak{M})$
.
$K(\mathfrak{M})$
.
(i) Module structure. The action of
 $K(\text{DM})$
on
$K(\text{DM})$
on
 $K(\mathfrak{M})$
, given by
$K(\mathfrak{M})$
, given by
 $[Z]\cdot [X\rightarrow \mathfrak{M}]=[Z\times X\rightarrow X\rightarrow \mathfrak{M}]$
, which turns
$[Z]\cdot [X\rightarrow \mathfrak{M}]=[Z\times X\rightarrow X\rightarrow \mathfrak{M}]$
, which turns
 $K(\mathfrak{M})$
into a
$K(\mathfrak{M})$
into a
 $K(\text{DM})$
-module.
$K(\text{DM})$
-module.(ii) Multiplication. The commutative multiplication given by
 $$\begin{eqnarray}[X\rightarrow \mathfrak{M}]\cdot [Y\rightarrow \mathfrak{M}]=[X\times Y\rightarrow \mathfrak{M}\times \mathfrak{M}\stackrel{\oplus }{\longrightarrow }\mathfrak{M}].\end{eqnarray}$$
$$\begin{eqnarray}[X\rightarrow \mathfrak{M}]\cdot [Y\rightarrow \mathfrak{M}]=[X\times Y\rightarrow \mathfrak{M}\times \mathfrak{M}\stackrel{\oplus }{\longrightarrow }\mathfrak{M}].\end{eqnarray}$$
(iii) Hall product. The Hall product of the stack functions
 $[X\rightarrow \mathfrak{M}]$
and
$[X\rightarrow \mathfrak{M}]$
and
 $[Y\rightarrow \mathfrak{M}]$
, which is defined by first constructing the fibred productand then setting
$[Y\rightarrow \mathfrak{M}]$
, which is defined by first constructing the fibred productand then setting
 $$\begin{eqnarray}[X\rightarrow \mathfrak{M}]\ast [Y\rightarrow \mathfrak{M}]=[X\ast Y\longrightarrow \mathfrak{M}^{(2)}\stackrel{b}{\longrightarrow }\mathfrak{M}].\end{eqnarray}$$
$$\begin{eqnarray}[X\rightarrow \mathfrak{M}]\ast [Y\rightarrow \mathfrak{M}]=[X\ast Y\longrightarrow \mathfrak{M}^{(2)}\stackrel{b}{\longrightarrow }\mathfrak{M}].\end{eqnarray}$$
The multiplication is associative and commutative; the Hall product is associative. The unit with respect to both multiplications is given by the
![]() $0$
-object of
$0$
-object of
![]() $\mathfrak{M}$
:
$\mathfrak{M}$
:
We will refer to
![]() $K(\mathfrak{M})$
as the Hall algebra of
$K(\mathfrak{M})$
as the Hall algebra of
![]() $\mathfrak{M}$
.
$\mathfrak{M}$
.
We define, inductively,
![]() $\mathfrak{M}^{(n)}$
, for
$\mathfrak{M}^{(n)}$
, for
![]() $n\geqslant 3$
, by the following cartesian diagram.
$n\geqslant 3$
, by the following cartesian diagram.

The stack
![]() $\mathfrak{M}^{(n)}$
comes with structure maps
$\mathfrak{M}^{(n)}$
comes with structure maps
![]() $a_{1},\ldots ,a_{n},b:\mathfrak{M}^{(n)}\rightarrow \mathfrak{M}$
, defined recursively by
$a_{1},\ldots ,a_{n},b:\mathfrak{M}^{(n)}\rightarrow \mathfrak{M}$
, defined recursively by
![]() $a_{i}=a_{i}\circ p_{1}$
, for
$a_{i}=a_{i}\circ p_{1}$
, for
![]() $i<n$
, and
$i<n$
, and
![]() $a_{n}=a_{2}\circ p_{2}$
, and
$a_{n}=a_{2}\circ p_{2}$
, and
![]() $b=b\circ p_{2}$
. The stack
$b=b\circ p_{2}$
. The stack
![]() $\mathfrak{M}^{(n)}$
is the stack of objects in
$\mathfrak{M}^{(n)}$
is the stack of objects in
![]() $\mathfrak{M}$
endowed with filtrations of length
$\mathfrak{M}$
endowed with filtrations of length
![]() $n$
. The subquotients are given by the maps
$n$
. The subquotients are given by the maps
![]() $a_{1},\ldots ,a_{n}$
, and the ‘total object’ by
$a_{1},\ldots ,a_{n}$
, and the ‘total object’ by
![]() $b$
.
$b$
.
It follows from the axioms for exact categories that there is also the following cartesian diagram.

The case
![]() $n=3$
is known as Noether’s isomorphism (see, for example, [Reference BühlerBüh10, Lemma 3.5]) and is responsible for the associativity of the Hall product.
$n=3$
is known as Noether’s isomorphism (see, for example, [Reference BühlerBüh10, Lemma 3.5]) and is responsible for the associativity of the Hall product.
3.1 Filtered structure of the Hall algebra
Definition 3.2. For
![]() $n\geqslant 0$
, we define
$n\geqslant 0$
, we define
This is an ascending filtration on
![]() $K(\mathfrak{M})$
, called the filtration by the order of vanishing of inertia at
$K(\mathfrak{M})$
, called the filtration by the order of vanishing of inertia at
![]() $q=1$
, or simply the order filtration of
$q=1$
, or simply the order filtration of
![]() $K(\mathfrak{M})$
.
$K(\mathfrak{M})$
.
This is a slight abuse of language, because only the space obtained by extension of scalars
![]() $K^{{\leqslant}n}(\mathfrak{M})_{(q-1)}$
is the direct sum of all eigenspaces of
$K^{{\leqslant}n}(\mathfrak{M})_{(q-1)}$
is the direct sum of all eigenspaces of
![]() $I^{\circ ,\text{ss}}$
whose corresponding eigenvalues
$I^{\circ ,\text{ss}}$
whose corresponding eigenvalues
![]() $\mathscr{Q}\in \mathbb{Q}[q]$
have order of vanishing at
$\mathscr{Q}\in \mathbb{Q}[q]$
have order of vanishing at
![]() $q=1$
less than or equal to
$q=1$
less than or equal to
![]() $n$
.
$n$
.
Theorem 3.3. Suppose that
![]() $\unicode[STIX]{x1D709}\in K^{{\leqslant}n}(\mathfrak{M})$
and
$\unicode[STIX]{x1D709}\in K^{{\leqslant}n}(\mathfrak{M})$
and
![]() $\unicode[STIX]{x1D712}\in K^{{\leqslant}m}(\mathfrak{M})$
. Then,
$\unicode[STIX]{x1D712}\in K^{{\leqslant}m}(\mathfrak{M})$
. Then,
![]() $\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}\in K^{{\leqslant}n+m}(\mathfrak{M})$
. Moreover, we have
$\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}\in K^{{\leqslant}n+m}(\mathfrak{M})$
. Moreover, we have
To prove this theorem we will prove the following lemma.
Lemma 3.4. For any two stack functions
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D712}\in K(\mathfrak{M})$
and for any integer
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D712}\in K(\mathfrak{M})$
and for any integer
![]() $p\geqslant 0$
, we have
$p\geqslant 0$
, we have
as an equation in
![]() $K(\mathfrak{M})[t]$
.
$K(\mathfrak{M})[t]$
.
Before proving the lemma, let us indicate how the lemma implies the theorem. For this, suppose that
![]() $\unicode[STIX]{x1D709}\in K^{{\leqslant}k}(\mathfrak{M})$
and
$\unicode[STIX]{x1D709}\in K^{{\leqslant}k}(\mathfrak{M})$
and
![]() $\unicode[STIX]{x1D712}\in K^{{\leqslant}\ell }(\mathfrak{M})$
. Then the degree of
$\unicode[STIX]{x1D712}\in K^{{\leqslant}\ell }(\mathfrak{M})$
. Then the degree of
![]() $\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})$
in
$\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})$
in
![]() $t$
is at most
$t$
is at most
![]() $k$
and the degree of
$k$
and the degree of
![]() $\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712})$
is at most
$\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712})$
is at most
![]() $\ell$
. So the degree of
$\ell$
. So the degree of
![]() $E_{p}(\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})\ast \unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712}))$
is at most
$E_{p}(\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})\ast \unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712}))$
is at most
![]() $k+\ell$
. So we see that if
$k+\ell$
. So we see that if
![]() $p>k+\ell$
, then
$p>k+\ell$
, then
![]() $E_{p}(\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})\ast \unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712}))=0$
, which implies that
$E_{p}(\unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D709})\ast \unicode[STIX]{x1D70B}_{t}(\unicode[STIX]{x1D712}))=0$
, which implies that
![]() $\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}\in K^{{\leqslant}k+\ell }(\mathfrak{M})$
, by Corollary 2.8.
$\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}\in K^{{\leqslant}k+\ell }(\mathfrak{M})$
, by Corollary 2.8.
Now set
![]() $p=k+\ell$
. The left-hand side of (19) has degree at most
$p=k+\ell$
. The left-hand side of (19) has degree at most
![]() $k+\ell$
, the right-hand side has degree exactly
$k+\ell$
, the right-hand side has degree exactly
![]() $k+\ell$
, which implies that both sides are homogeneous of degree
$k+\ell$
, which implies that both sides are homogeneous of degree
![]() $k+\ell$
, and we have
$k+\ell$
, and we have
Now notice that if
![]() $x\in K^{{\leqslant}n}(\mathfrak{M})$
, we have
$x\in K^{{\leqslant}n}(\mathfrak{M})$
, we have
![]() $\unicode[STIX]{x1D70B}_{n}(x)=(1/n!)E_{n}(x)$
. Hence, we can rewrite our equation as
$\unicode[STIX]{x1D70B}_{n}(x)=(1/n!)E_{n}(x)$
. Hence, we can rewrite our equation as
This proves the theorem.
Analysis of
 $E_{p}(E_{n}\ast E_{m})$
$E_{p}(E_{n}\ast E_{m})$
Suppose
![]() $\unicode[STIX]{x1D709}=(X\rightarrow \mathfrak{M})$
and
$\unicode[STIX]{x1D709}=(X\rightarrow \mathfrak{M})$
and
![]() $\unicode[STIX]{x1D712}=(Y\rightarrow \mathfrak{M})$
are stack functions. The stack function
$\unicode[STIX]{x1D712}=(Y\rightarrow \mathfrak{M})$
are stack functions. The stack function
![]() $\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}$
is defined by the following cartesian diagram.
$\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712}$
is defined by the following cartesian diagram.

Explicitly,
![]() $X\ast Y$
is the stack of triples
$X\ast Y$
is the stack of triples
![]() $(x,M,y)$
$(x,M,y)$

where
![]() $x$
and
$x$
and
![]() $y$
are objects of
$y$
are objects of
![]() $X$
and
$X$
and
![]() $Y$
, respectively,
$Y$
, respectively,
![]() $M$
is an object of
$M$
is an object of
![]() $\mathfrak{M}^{(2)}$
, i.e., a short exact sequence
$\mathfrak{M}^{(2)}$
, i.e., a short exact sequence
![]() $M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
of objects in
$M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
of objects in
![]() $\mathfrak{M}$
, and
$\mathfrak{M}$
, and
![]() $x\rightarrow M^{\prime }$
and
$x\rightarrow M^{\prime }$
and
![]() $y\rightarrow M^{\prime \prime }$
are isomorphisms from the images of
$y\rightarrow M^{\prime \prime }$
are isomorphisms from the images of
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $\mathfrak{M}$
to
$\mathfrak{M}$
to
![]() $M^{\prime }$
and
$M^{\prime }$
and
![]() $M^{\prime \prime }$
, respectively. (We omit these isomorphisms from the triple to simplify the notation.)
$M^{\prime \prime }$
, respectively. (We omit these isomorphisms from the triple to simplify the notation.)
The stack function
![]() $E_{n}(\unicode[STIX]{x1D709})\ast E_{m}(\unicode[STIX]{x1D712})$
is defined by the following enlarged diagram.
$E_{n}(\unicode[STIX]{x1D709})\ast E_{m}(\unicode[STIX]{x1D712})$
is defined by the following enlarged diagram.

Explicitly,
![]() $E_{n}(X)\ast E_{m}(Y)$
is the stack of 5-tuples
$E_{n}(X)\ast E_{m}(Y)$
is the stack of 5-tuples
![]() $(x,(e_{\unicode[STIX]{x1D708}}),M,y,(f_{\unicode[STIX]{x1D707}}))$
, where
$(x,(e_{\unicode[STIX]{x1D708}}),M,y,(f_{\unicode[STIX]{x1D707}}))$
, where
![]() $(x,M,y)$
represents a diagram (20),
$(x,M,y)$
represents a diagram (20),
![]() $(e_{\unicode[STIX]{x1D708}})=(e_{1},\ldots ,e_{n})$
is a complete set of non-zero orthogonal idempotents in
$(e_{\unicode[STIX]{x1D708}})=(e_{1},\ldots ,e_{n})$
is a complete set of non-zero orthogonal idempotents in
![]() $A(x)$
, and
$A(x)$
, and
![]() $(f_{\unicode[STIX]{x1D707}})=(f_{1},\ldots ,f_{m})$
is a complete set of non-zero orthogonal idempotents in
$(f_{\unicode[STIX]{x1D707}})=(f_{1},\ldots ,f_{m})$
is a complete set of non-zero orthogonal idempotents in
![]() $A(y)$
.
$A(y)$
.
Finally, the stack
![]() $E_{p}(E_{n}(X)\ast E_{m}(Y))$
is the stack of objects of
$E_{p}(E_{n}(X)\ast E_{m}(Y))$
is the stack of objects of
![]() $E_{n}(X)\ast E_{m}(Y)$
endowed with a complete set of
$E_{n}(X)\ast E_{m}(Y)$
endowed with a complete set of
![]() $p$
non-zero labelled idempotents. Explicitly, it consists of 6-tuples
$p$
non-zero labelled idempotents. Explicitly, it consists of 6-tuples
where
![]() $(x,M,y)$
is as in (20) and
$(x,M,y)$
is as in (20) and
![]() $(g_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of non-zero orthogonal idempotent endomorphisms of the short exact sequence
$(g_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p}}$
is a complete set of non-zero orthogonal idempotent endomorphisms of the short exact sequence
![]() $M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
. Moreover,
$M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }$
. Moreover,
![]() $(e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p},\unicode[STIX]{x1D708}\in \text{}\underline{n}}$
is a
$(e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p},\unicode[STIX]{x1D708}\in \text{}\underline{n}}$
is a
![]() $pn$
-tuple of orthogonal idempotents in
$pn$
-tuple of orthogonal idempotents in
![]() $A(x)$
and
$A(x)$
and
![]() $(f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p},\unicode[STIX]{x1D707}\in \text{}\underline{m}}$
is a
$(f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}})_{\unicode[STIX]{x1D70C}\in \text{}\underline{p},\unicode[STIX]{x1D707}\in \text{}\underline{m}}$
is a
![]() $pm$
-tuple of orthogonal idempotents in
$pm$
-tuple of orthogonal idempotents in
![]() $A(y)$
such that for every
$A(y)$
such that for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
we have
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
we have
![]() $\sum _{\unicode[STIX]{x1D708}=1}^{n}e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}}=g_{\unicode[STIX]{x1D70C}}|_{M^{\prime }}$
and
$\sum _{\unicode[STIX]{x1D708}=1}^{n}e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}}=g_{\unicode[STIX]{x1D70C}}|_{M^{\prime }}$
and
![]() $\sum _{\unicode[STIX]{x1D707}=1}^{m}f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}}=g_{\unicode[STIX]{x1D70C}}|_{M^{\prime \prime }}$
. Finally, we require for all
$\sum _{\unicode[STIX]{x1D707}=1}^{m}f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}}=g_{\unicode[STIX]{x1D70C}}|_{M^{\prime \prime }}$
. Finally, we require for all
![]() $\unicode[STIX]{x1D708}=1,\ldots ,n$
that
$\unicode[STIX]{x1D708}=1,\ldots ,n$
that
![]() $e_{\unicode[STIX]{x1D708}}=\sum _{\unicode[STIX]{x1D70C}=1}^{p}e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}}\not =0$
and for all
$e_{\unicode[STIX]{x1D708}}=\sum _{\unicode[STIX]{x1D70C}=1}^{p}e_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D708}}\not =0$
and for all
![]() $\unicode[STIX]{x1D707}=1,\ldots ,m$
that
$\unicode[STIX]{x1D707}=1,\ldots ,m$
that
![]() $f_{\unicode[STIX]{x1D707}}=\sum _{\unicode[STIX]{x1D70C}=1}^{p}f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}}\not =0$
.
$f_{\unicode[STIX]{x1D707}}=\sum _{\unicode[STIX]{x1D70C}=1}^{p}f_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D707}}\not =0$
.
Decomposing
 $E_{p}(E_{n}\ast E_{m})$
$E_{p}(E_{n}\ast E_{m})$
Given
![]() $p$
-tuples of non-negative integers
$p$
-tuples of non-negative integers
![]() $\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{p})$
and
$\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{p})$
and
![]() $\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{p})$
, we define a new stack function
$\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{p})$
, we define a new stack function
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}\rightarrow \mathfrak{M}$
, denoted by
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}\rightarrow \mathfrak{M}$
, denoted by
![]() $(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
, as follows.
$(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
, as follows.
Let
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
be the algebraic stack of 6-tuples
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
be the algebraic stack of 6-tuples
where
![]() $(x,M,y)$
is as in (20) and
$(x,M,y)$
is as in (20) and
![]() $(g_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}=1,\ldots ,p}$
is a complete set of non-zero orthogonal idempotent endomorphisms of the short exact
$(g_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D70C}=1,\ldots ,p}$
is a complete set of non-zero orthogonal idempotent endomorphisms of the short exact
![]() $M$
. Moreover, for every
$M$
. Moreover, for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, we require that
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, we require that
![]() $e_{\unicode[STIX]{x1D70C}}=(e_{1},\ldots ,e_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}})$
and
$e_{\unicode[STIX]{x1D70C}}=(e_{1},\ldots ,e_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}})$
and
![]() $f_{\unicode[STIX]{x1D70C}}=(f_{1},\ldots ,f_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}})$
are families of non-zero orthogonal idempotents for
$f_{\unicode[STIX]{x1D70C}}=(f_{1},\ldots ,f_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}})$
are families of non-zero orthogonal idempotents for
![]() $x$
and
$x$
and
![]() $y$
, respectively, such that for all
$y$
, respectively, such that for all
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
,
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
,
It follows that the union of
![]() $e_{1},\ldots ,e_{p}$
is a complete set of orthogonal idempotents for
$e_{1},\ldots ,e_{p}$
is a complete set of orthogonal idempotents for
![]() $x$
and the union of
$x$
and the union of
![]() $f_{1},\ldots ,f_{p}$
is a complete set of orthogonal idempotents for
$f_{1},\ldots ,f_{p}$
is a complete set of orthogonal idempotents for
![]() $y$
.
$y$
.
There is a natural algebroid structure on
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
. The morphism to
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
. The morphism to
![]() $\mathfrak{M}$
given by mapping the
$\mathfrak{M}$
given by mapping the
![]() $6$
-tuple (22) to the middle object
$6$
-tuple (22) to the middle object
![]() $b(M)$
of the short exact sequence
$b(M)$
of the short exact sequence
![]() $M$
makes
$M$
makes
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
into a stack function.
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
into a stack function.
Note that if for some
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, both integers
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, both integers
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
and
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
and
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
vanish, then
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
vanish, then
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}=\varnothing$
, because all
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}=\varnothing$
, because all
![]() $g_{\unicode[STIX]{x1D70C}}$
are required to be non-zero.
$g_{\unicode[STIX]{x1D70C}}$
are required to be non-zero.
Let us write
![]() $|\unicode[STIX]{x1D711}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
and
$|\unicode[STIX]{x1D711}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
and
![]() $|\unicode[STIX]{x1D713}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
. Let us assume that for every
$|\unicode[STIX]{x1D713}|=\sum _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
. Let us assume that for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of the two integers
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of the two integers
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero. Then we have a morphism
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero. Then we have a morphism
which maps a quadruple
![]() $(x,(e_{\unicode[STIX]{x1D714}}),y,(f_{\unicode[STIX]{x1D702}}))$
to the 6-tuple (22) where
$(x,(e_{\unicode[STIX]{x1D714}}),y,(f_{\unicode[STIX]{x1D702}}))$
to the 6-tuple (22) where
![]() $M=M^{\prime }\oplus M^{\prime \prime }$
, with
$M=M^{\prime }\oplus M^{\prime \prime }$
, with
![]() $M^{\prime }$
denoting the image of
$M^{\prime }$
denoting the image of
![]() $x$
in
$x$
in
![]() $\mathfrak{M}$
and
$\mathfrak{M}$
and
![]() $M^{\prime \prime }$
the image of
$M^{\prime \prime }$
the image of
![]() $y$
in
$y$
in
![]() $\mathfrak{M}$
. To define (24), we break up the complete family of orthogonal idempotents
$\mathfrak{M}$
. To define (24), we break up the complete family of orthogonal idempotents
![]() $e_{1},\ldots ,e_{|\unicode[STIX]{x1D711}|}$
for
$e_{1},\ldots ,e_{|\unicode[STIX]{x1D711}|}$
for
![]() $x$
into
$x$
into
![]() $p$
subfamilies, where the
$p$
subfamilies, where the
![]() $\unicode[STIX]{x1D70C}$
th subfamily has
$\unicode[STIX]{x1D70C}$
th subfamily has
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
members. Similarly, we break up
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
members. Similarly, we break up
![]() $f_{1},\ldots ,f_{|\unicode[STIX]{x1D713}|}$
into
$f_{1},\ldots ,f_{|\unicode[STIX]{x1D713}|}$
into
![]() $p$
subfamilies whose sizes are
$p$
subfamilies whose sizes are
![]() $\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{p}$
. Then the family of idempotents
$\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{p}$
. Then the family of idempotents
![]() $(g_{\unicode[STIX]{x1D70C}})$
on
$(g_{\unicode[STIX]{x1D70C}})$
on
![]() $M$
is defined by formulas (23). Note that we need to make our assumption on the
$M$
is defined by formulas (23). Note that we need to make our assumption on the
![]() $p$
-tuples
$p$
-tuples
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $\unicode[STIX]{x1D713}$
, in order for every family member
$\unicode[STIX]{x1D713}$
, in order for every family member
![]() $g_{\unicode[STIX]{x1D70C}}$
to be non-zero.
$g_{\unicode[STIX]{x1D70C}}$
to be non-zero.
Lemma 3.5. If for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, exactly one of the two integers
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, exactly one of the two integers
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero, (24) is an isomorphism. Hence, we have the equality
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero, (24) is an isomorphism. Hence, we have the equality
for stack functions.
Proof. Given an object (22) of
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
, the short exact sequence
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
, the short exact sequence
![]() $M$
is split into a direct sum of
$M$
is split into a direct sum of
![]() $p$
short exact sequences. Each one of these sequences is canonically split, because either the subobject or the quotient object vanishes, by the assumption on
$p$
short exact sequences. Each one of these sequences is canonically split, because either the subobject or the quotient object vanishes, by the assumption on
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D713}$
. Therefore, the sequence
$\unicode[STIX]{x1D713}$
. Therefore, the sequence
![]() $M$
is split, canonically, too.◻
$M$
is split, canonically, too.◻
Now suppose we are given strictly monotone maps
for all
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
such that the images of the
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
such that the images of the
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70C}}$
cover
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70C}}$
cover
![]() $\text{}\underline{n}$
and the images of the
$\text{}\underline{n}$
and the images of the
![]() $\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70C}}$
cover
$\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70C}}$
cover
![]() $\text{}\underline{m}$
. The choice of these injections determines a morphism of algebraic stacks
$\text{}\underline{m}$
. The choice of these injections determines a morphism of algebraic stacks
by mapping the
![]() $6$
-tuple (22) to the 6-tuple (21) by defining
$6$
-tuple (22) to the 6-tuple (21) by defining
By our assumptions, these sums are either empty or consist of a single summand, so the
![]() $e_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D70C}}$
and the
$e_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D70C}}$
and the
![]() $f_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}}$
are obtained from the
$f_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}}$
are obtained from the
![]() $(e_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D714}}$
and the
$(e_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D714}}$
and the
![]() $(f_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D702}}$
essentially by relabelling.
$(f_{\unicode[STIX]{x1D70C}})_{\unicode[STIX]{x1D702}}$
essentially by relabelling.
Note that the requirements
![]() $\bigcup _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70C}}(\text{}\underline{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}})=\text{}\underline{n}$
and
$\bigcup _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D70C}}(\text{}\underline{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}})=\text{}\underline{n}$
and
![]() $\bigcup _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70C}}(\text{}\underline{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}})=\text{}\underline{m}$
are needed to assure that
$\bigcup _{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D6F9}_{\unicode[STIX]{x1D70C}}(\text{}\underline{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}})=\text{}\underline{m}$
are needed to assure that
![]() $\sum _{\unicode[STIX]{x1D70C}}e_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D70C}}$
and
$\sum _{\unicode[STIX]{x1D70C}}e_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D70C}}$
and
![]() $\sum _{\unicode[STIX]{x1D70C}}f_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}}$
are non-zero, for all
$\sum _{\unicode[STIX]{x1D70C}}f_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D70C}}$
are non-zero, for all
![]() $\unicode[STIX]{x1D708}=1,\ldots ,n$
and
$\unicode[STIX]{x1D708}=1,\ldots ,n$
and
![]() $\unicode[STIX]{x1D707}=1,\ldots ,m$
.
$\unicode[STIX]{x1D707}=1,\ldots ,m$
.
Lemma 3.6. The morphism (25) gives rise to a morphism of stack functions
![]() $(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}\rightarrow E_{p}(E_{n}(\unicode[STIX]{x1D709})\ast E_{m}(\unicode[STIX]{x1D712}))$
, which is both an open and a closed immersion.
$(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}\rightarrow E_{p}(E_{n}(\unicode[STIX]{x1D709})\ast E_{m}(\unicode[STIX]{x1D712}))$
, which is both an open and a closed immersion.
If we change any of
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $\unicode[STIX]{x1D713}$
, or
$\unicode[STIX]{x1D713}$
, or
![]() $\unicode[STIX]{x1D6F7}$
,
$\unicode[STIX]{x1D6F7}$
,
![]() $\unicode[STIX]{x1D6F9}$
, we get a morphism with disjoint image. The images of all morphisms (25) cover
$\unicode[STIX]{x1D6F9}$
, we get a morphism with disjoint image. The images of all morphisms (25) cover
![]() $E_{p}(E_{n}(X)\ast E_{m}(Y))$
.
$E_{p}(E_{n}(X)\ast E_{m}(Y))$
.
Proof. This follows from the fact that the source and target of (25) differ only in the way the idempotents in
![]() $A_{x}$
and
$A_{x}$
and
![]() $A_{y}$
are indexed.◻
$A_{y}$
are indexed.◻
Corollary 3.7. Using the notation introduced in (18), we have the following equation in
![]() $K(\mathfrak{M})$
:
$K(\mathfrak{M})$
:
where
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D713}$
run over all
$\unicode[STIX]{x1D713}$
run over all
![]() $p$
-tuples of non-negative integers.
$p$
-tuples of non-negative integers.
For example, consider
![]() $\unicode[STIX]{x1D712}=1$
and
$\unicode[STIX]{x1D712}=1$
and
![]() $m=0$
. If any of the
$m=0$
. If any of the
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero,
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero,
![]() $(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
is empty. Hence,
$(X\ast Y)_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
is empty. Hence,
where the sum is over all
![]() $p$
-tuples of positive integers.
$p$
-tuples of positive integers.
Proof of the main lemma
Using Proposition 2.24, we can now calculate as follows:

For example, if
![]() $\unicode[STIX]{x1D712}=1$
, we get
$\unicode[STIX]{x1D712}=1$
, we get
The lowest order term in (26) has degree
![]() $p$
, since for
$p$
, since for
![]() $(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
not to vanish, we need, for every
$(\unicode[STIX]{x1D709}\ast \unicode[STIX]{x1D712})_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}}$
not to vanish, we need, for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
, at least one of
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
to be non-zero.
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
to be non-zero.
Modulo
![]() $(t^{p+1})$
, only terms corresponding to pairs
$(t^{p+1})$
, only terms corresponding to pairs
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, with the property that for every
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, with the property that for every
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,p$
exactly one of
$\unicode[STIX]{x1D70C}=1,\ldots ,p$
exactly one of
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70C}}$
,
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero, contribute to (26). These are exactly the terms to which Lemma 3.5 applies, and we deduce that, modulo
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70C}}$
is non-zero, contribute to (26). These are exactly the terms to which Lemma 3.5 applies, and we deduce that, modulo
![]() $t^{p+1}$
, we have:
$t^{p+1}$
, we have:
where the sum is over all
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, where the supports of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, where the supports of
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D713}$
form a partition of
$\unicode[STIX]{x1D713}$
form a partition of
![]() $\text{}\underline{p}$
. By grouping terms corresponding to partitions of the same size together, we can rewrite this as
$\text{}\underline{p}$
. By grouping terms corresponding to partitions of the same size together, we can rewrite this as
which is equal to
by (27). Modulo
![]() $t^{p+1}$
, this term is congruent to
$t^{p+1}$
, this term is congruent to
We conclude that
which proves Lemma 3.4.
3.2 The semi-classical Hall algebra
By Theorem 3.3, the submodule
of
![]() $K(\mathfrak{M})[t]$
is a
$K(\mathfrak{M})[t]$
is a
![]() $K(\text{DM})[t]$
-subalgebra with respect to the Hall product. The algebra
$K(\text{DM})[t]$
-subalgebra with respect to the Hall product. The algebra
![]() $\mathscr{K}(\mathfrak{M})$
is a one-parameter flat family of algebras. The special fibre at
$\mathscr{K}(\mathfrak{M})$
is a one-parameter flat family of algebras. The special fibre at
![]() $t=0$
is canonically isomorphic to the graded algebra associated to the filtered algebra
$t=0$
is canonically isomorphic to the graded algebra associated to the filtered algebra
![]() $(K(\mathfrak{M}),\ast )$
. The quotient map
$(K(\mathfrak{M}),\ast )$
. The quotient map
![]() $\mathscr{K}\rightarrow \mathscr{K}/t\mathscr{K}$
is identified with the map
$\mathscr{K}\rightarrow \mathscr{K}/t\mathscr{K}$
is identified with the map
![]() $\sum _{n}x_{n}t^{n}\mapsto \sum _{n}\unicode[STIX]{x1D70B}_{n}(x_{n})$
.
$\sum _{n}x_{n}t^{n}\mapsto \sum _{n}\unicode[STIX]{x1D70B}_{n}(x_{n})$
.
The graded algebra associated to the filtered algebra
![]() $(K(\mathfrak{M}),\ast )$
is canonically isomorphic to the commutative graded algebra
$(K(\mathfrak{M}),\ast )$
is canonically isomorphic to the commutative graded algebra
![]() $(K(\mathfrak{M}),\,\cdot \,)$
, by Theorem 3.3. The special fibre inherits therefore a Poisson bracket, which encodes the Hall product to second order. This Poisson bracket has degree
$(K(\mathfrak{M}),\,\cdot \,)$
, by Theorem 3.3. The special fibre inherits therefore a Poisson bracket, which encodes the Hall product to second order. This Poisson bracket has degree
![]() $-1$
and is given by the formula
$-1$
and is given by the formula
Corollary 3.8. The graded
![]() $K(\text{DM})$
-algebra
$K(\text{DM})$
-algebra
![]() $(K(\mathfrak{M}),\,\cdot \,)$
is endowed with a Poisson bracket of degree
$(K(\mathfrak{M}),\,\cdot \,)$
is endowed with a Poisson bracket of degree
![]() $-1$
, given by (28).
$-1$
, given by (28).
Corollary 3.9. In particular,
![]() $K^{1}(\mathfrak{M})$
is a Lie algebra with respect to the Poisson bracket (28). In fact, for
$K^{1}(\mathfrak{M})$
is a Lie algebra with respect to the Poisson bracket (28). In fact, for
![]() $x,y\in K^{1}(\mathfrak{M})$
, we have that
$x,y\in K^{1}(\mathfrak{M})$
, we have that
![]() $x\ast y-y\ast x\in K^{1}(\mathfrak{M})$
, so in this case, the Poisson bracket is equal to the Lie bracket. Thus,
$x\ast y-y\ast x\in K^{1}(\mathfrak{M})$
, so in this case, the Poisson bracket is equal to the Lie bracket. Thus,
![]() $K^{1}(\mathfrak{M})$
is a Lie algebra over the ring of scalars
$K^{1}(\mathfrak{M})$
is a Lie algebra over the ring of scalars
![]() $K(\text{DM})$
.
$K(\text{DM})$
.
Proof. Equation (26) for
![]() $p=0$
, together with Lemma 3.5, says
$p=0$
, together with Lemma 3.5, says
This proves that
![]() $E_{0}(x)=0$
or
$E_{0}(x)=0$
or
![]() $E_{0}(y)=0$
implies that
$E_{0}(y)=0$
implies that
![]() $E_{0}(x\ast y)=0$
.◻
$E_{0}(x\ast y)=0$
.◻
Definition 3.10. We call
![]() $K^{1}(\mathfrak{M})$
the Lie algebra of virtually indecomposable stack functions. We will usually write
$K^{1}(\mathfrak{M})$
the Lie algebra of virtually indecomposable stack functions. We will usually write
![]() $K^{\text{vir}}(\mathfrak{M})$
for
$K^{\text{vir}}(\mathfrak{M})$
for
![]() $K^{1}(\mathfrak{M})$
.
$K^{1}(\mathfrak{M})$
.
This terminology is used in analogy with that of [Reference JoyceJoy07a]. In Appendix A, we check that our notion of virtually indecomposable agrees with that of [Reference JoyceJoy07a] in a special case.
3.3 Epsilon functions
We will prove that replacing direct sum decompositions by filtrations, in the formula
will give rise to an operator mapping
![]() $K(\mathfrak{M})$
into
$K(\mathfrak{M})$
into
![]() $K^{{\leqslant}k}(\mathfrak{M})$
. In particular, we will be able to construct virtually indecomposable stack functions as ‘Hall algebra logarithms’.
$K^{{\leqslant}k}(\mathfrak{M})$
. In particular, we will be able to construct virtually indecomposable stack functions as ‘Hall algebra logarithms’.
Fix an algebraic substack
![]() $\mathfrak{N}{\hookrightarrow}\mathfrak{M}$
with the following properties:
$\mathfrak{N}{\hookrightarrow}\mathfrak{M}$
with the following properties:
(i)
 $\mathfrak{N}$
avoids the image of
$\mathfrak{N}$
avoids the image of
 $\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
;
$\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
;(ii)
 $\mathfrak{N}$
is closed under direct sums and direct summands, i.e., it is Karoubian (Remark 1.63) if we add
$\mathfrak{N}$
is closed under direct sums and direct summands, i.e., it is Karoubian (Remark 1.63) if we add
 $\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
to it;
$\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
to it;(iii) for every positive integer
 $n$
, the morphism
$n$
, the morphism
 $b|_{\mathfrak{N}^{(n)}}:\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
, illustrated in the diagram(29)where the square is cartesian, is of finite type;
$b|_{\mathfrak{N}^{(n)}}:\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
, illustrated in the diagram(29)where the square is cartesian, is of finite type;
(iv) the disjoint union over all these morphisms
 $\coprod _{n>0}\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
is still of finite type. This means that if
$\coprod _{n>0}\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
is still of finite type. This means that if
 $X\rightarrow \mathfrak{M}$
is a morphism with
$X\rightarrow \mathfrak{M}$
is a morphism with
 $X$
of finite type, there exists an
$X$
of finite type, there exists an
 $N>0$
such that for all
$N>0$
such that for all
 $n\geqslant N$
, the image of
$n\geqslant N$
, the image of
 $b|_{\mathfrak{N}^{(n)}}:\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
does not intersect the image of
$b|_{\mathfrak{N}^{(n)}}:\mathfrak{N}^{(n)}\rightarrow \mathfrak{M}$
does not intersect the image of
 $X$
in
$X$
in
 $\mathfrak{M}$
.
$\mathfrak{M}$
.
Example 3.11. If
![]() $\mathfrak{M}$
is the stack of coherent sheaves on a projective curve, then the substack of non-zero semi-stable vector bundles of fixed slope is an example of a substack
$\mathfrak{M}$
is the stack of coherent sheaves on a projective curve, then the substack of non-zero semi-stable vector bundles of fixed slope is an example of a substack
![]() $\mathfrak{N}$
satisfying our conditions. More generally, we can take for
$\mathfrak{N}$
satisfying our conditions. More generally, we can take for
![]() $\mathfrak{N}$
the stack of all vector bundles whose Harder–Narasimhan slopes are contained in a fixed interval.
$\mathfrak{N}$
the stack of all vector bundles whose Harder–Narasimhan slopes are contained in a fixed interval.
Example 3.12. If
![]() $\mathfrak{M}$
is the stack of representations of a quiver
$\mathfrak{M}$
is the stack of representations of a quiver
![]() $Q$
, then we can take
$Q$
, then we can take
![]() $\mathfrak{N}=\mathfrak{M}_{\ast }$
.
$\mathfrak{N}=\mathfrak{M}_{\ast }$
.
Consider an arbitrary stack function
![]() $X\rightarrow \mathfrak{M}$
, and denote by
$X\rightarrow \mathfrak{M}$
, and denote by
![]() $F_{n}X$
, for
$F_{n}X$
, for
![]() $n\geqslant 1$
, the stack
$n\geqslant 1$
, the stack
It fits into the following cartesian diagram.

Note that
![]() $F_{n}X$
is of finite type, by our assumption on
$F_{n}X$
is of finite type, by our assumption on
![]() $\mathfrak{N}$
, and also representable over
$\mathfrak{N}$
, and also representable over
![]() $\mathfrak{M}$
(as an algebroid), because
$\mathfrak{M}$
(as an algebroid), because
![]() $b$
is. Therefore,
$b$
is. Therefore,
![]() $F_{n}X$
is another stack function.
$F_{n}X$
is another stack function.
The objects of
![]() $F_{n}X$
are pairs
$F_{n}X$
are pairs
![]() $(x,F)$
, where
$(x,F)$
, where
![]() $x$
is an object of
$x$
is an object of
![]() $X$
and
$X$
and
![]() $F=(F_{1}\rightarrow \cdots \rightarrow F_{n})$
is a flag in
$F=(F_{1}\rightarrow \cdots \rightarrow F_{n})$
is a flag in
![]() $F_{n}=M$
, where
$F_{n}=M$
, where
![]() $M$
is the image of
$M$
is the image of
![]() $x$
in
$x$
in
![]() $\mathfrak{M}$
such that all subquotients
$\mathfrak{M}$
such that all subquotients
![]() $F_{\unicode[STIX]{x1D708}}/F_{\unicode[STIX]{x1D708}-1}$
, for
$F_{\unicode[STIX]{x1D708}}/F_{\unicode[STIX]{x1D708}-1}$
, for
![]() $\unicode[STIX]{x1D708}=1,\ldots ,n$
, are in
$\unicode[STIX]{x1D708}=1,\ldots ,n$
, are in
![]() $\mathfrak{N}$
.
$\mathfrak{N}$
.
We now consider
![]() $E_{k}(F_{n}X)$
, for
$E_{k}(F_{n}X)$
, for
![]() $k\geqslant 0$
. This is the stack of triples
$k\geqslant 0$
. This is the stack of triples
where the pair
![]() $(x,F)$
is an object of
$(x,F)$
is an object of
![]() $F_{n}X$
and
$F_{n}X$
and
![]() $(e_{\unicode[STIX]{x1D705}})=(e_{1},\ldots ,e_{k})$
is a complete set of non-zero orthogonal idempotents in
$(e_{\unicode[STIX]{x1D705}})=(e_{1},\ldots ,e_{k})$
is a complete set of non-zero orthogonal idempotents in
![]() $A(X)$
such that for every
$A(X)$
such that for every
![]() $\unicode[STIX]{x1D705}=1,\ldots ,k$
the endomorphism of
$\unicode[STIX]{x1D705}=1,\ldots ,k$
the endomorphism of
![]() $M$
induced by
$M$
induced by
![]() $e_{\unicode[STIX]{x1D705}}$
respects the flag
$e_{\unicode[STIX]{x1D705}}$
respects the flag
![]() $F$
. For every
$F$
. For every
![]() $\unicode[STIX]{x1D708}=1,\ldots ,n$
, we therefore get an induced idempotent operator
$\unicode[STIX]{x1D708}=1,\ldots ,n$
, we therefore get an induced idempotent operator
These idempotents have the properties:
(i)
 $\sum _{\unicode[STIX]{x1D705}}f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}=1$
, for all
$\sum _{\unicode[STIX]{x1D705}}f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}=1$
, for all
 $\unicode[STIX]{x1D708}$
;
$\unicode[STIX]{x1D708}$
;(ii) for every
 $\unicode[STIX]{x1D705}$
, at least one of the
$\unicode[STIX]{x1D705}$
, at least one of the
 $f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}$
does not vanish.
$f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}$
does not vanish.
The stack
![]() $E_{k}(F_{n}X)$
decomposes into a disjoint union of substacks according to which of the idempotents
$E_{k}(F_{n}X)$
decomposes into a disjoint union of substacks according to which of the idempotents
![]() $(f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}})$
vanish.
$(f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}})$
vanish.
To make this decomposition precise, consider a sequence of positive integers
![]() $(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})$
. Define
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k})$
. Define
![]() $F_{\unicode[STIX]{x1D6FC}}X$
to be the stack of triples
$F_{\unicode[STIX]{x1D6FC}}X$
to be the stack of triples
Here,
![]() $x$
is an object of
$x$
is an object of
![]() $X$
, with image
$X$
, with image
![]() $M$
in
$M$
in
![]() $\mathfrak{M}$
, and
$\mathfrak{M}$
, and
![]() $(e_{\unicode[STIX]{x1D705}})$
is a complete set of orthogonal non-zero idempotents for
$(e_{\unicode[STIX]{x1D705}})$
is a complete set of orthogonal non-zero idempotents for
![]() $x$
that decomposes
$x$
that decomposes
![]() $M$
into a direct sum
$M$
into a direct sum
![]() $M=\bigoplus _{\unicode[STIX]{x1D705}}M_{\unicode[STIX]{x1D705}}$
. Moreover,
$M=\bigoplus _{\unicode[STIX]{x1D705}}M_{\unicode[STIX]{x1D705}}$
. Moreover,
![]() $F_{\unicode[STIX]{x1D705}}$
is a flag of length
$F_{\unicode[STIX]{x1D705}}$
is a flag of length
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}$
on
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}$
on
![]() $M_{\unicode[STIX]{x1D705}}$
, with subquotients in
$M_{\unicode[STIX]{x1D705}}$
, with subquotients in
![]() $\mathfrak{N}$
, for every
$\mathfrak{N}$
, for every
![]() $\unicode[STIX]{x1D705}=1,\ldots ,k$
.
$\unicode[STIX]{x1D705}=1,\ldots ,k$
.
For every
![]() $k$
-tuple of strictly monotone maps
$k$
-tuple of strictly monotone maps
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}:\text{}\underline{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}}{\hookrightarrow}\text{}\underline{n}$
, we define a morphism
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}:\text{}\underline{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}}{\hookrightarrow}\text{}\underline{n}$
, we define a morphism
by defining the flag
![]() $F$
on
$F$
on
![]() $M$
in terms of the
$M$
in terms of the
![]() $k$
-tuple of flags
$k$
-tuple of flags
![]() $(F_{\unicode[STIX]{x1D705}})$
by
$(F_{\unicode[STIX]{x1D705}})$
by
Note that the sum for fixed
![]() $\unicode[STIX]{x1D705}$
is not really a sum, it is just the largest of the subobjects
$\unicode[STIX]{x1D705}$
is not really a sum, it is just the largest of the subobjects
![]() $F_{\unicode[STIX]{x1D70C}}$
of
$F_{\unicode[STIX]{x1D70C}}$
of
![]() $M_{\unicode[STIX]{x1D705}}$
making up the flag
$M_{\unicode[STIX]{x1D705}}$
making up the flag
![]() $F_{1}\rightarrow \cdots \rightarrow F_{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}}$
such that
$F_{1}\rightarrow \cdots \rightarrow F_{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}}$
such that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D70C})\leqslant \unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D70C})\leqslant \unicode[STIX]{x1D708}$
.
Lemma 3.13. The morphism (30) given by
![]() $(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}})_{\unicode[STIX]{x1D705}\in \text{}\underline{k}}$
is an isomorphism onto the locus in
$(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}})_{\unicode[STIX]{x1D705}\in \text{}\underline{k}}$
is an isomorphism onto the locus in
![]() $E_{k}(F_{n}X)$
, defined by
$E_{k}(F_{n}X)$
, defined by
![]() $f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}\not =0$
if and only if
$f_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D708}}\not =0$
if and only if
![]() $\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}(\text{}\underline{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}})$
, for all
$\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D705}}(\text{}\underline{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}})$
, for all
![]() $\unicode[STIX]{x1D705}=1,\ldots ,k$
.
$\unicode[STIX]{x1D705}=1,\ldots ,k$
.
Corollary 3.14. If
![]() $\unicode[STIX]{x1D709}$
denotes the element of
$\unicode[STIX]{x1D709}$
denotes the element of
![]() $K(\mathfrak{M})$
defined by
$K(\mathfrak{M})$
defined by
![]() $X\rightarrow \mathfrak{M}$
, we have
$X\rightarrow \mathfrak{M}$
, we have
where the sum is taken over all
![]() $k$
-tuples of positive integers.
$k$
-tuples of positive integers.
If we set
![]() $F_{0}(\unicode[STIX]{x1D709})=1$
and
$F_{0}(\unicode[STIX]{x1D709})=1$
and
![]() $F_{\varnothing }(\unicode[STIX]{x1D709})=1$
, this equality also holds for
$F_{\varnothing }(\unicode[STIX]{x1D709})=1$
, this equality also holds for
![]() $n=0$
.
$n=0$
.
Definition 3.15. Define, for every
![]() $\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
,
$\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
,
where for
![]() $n=0$
, we set
$n=0$
, we set
![]() $F_{0}(\unicode[STIX]{x1D709})=1$
. This definition is justified, because by our assumptions on
$F_{0}(\unicode[STIX]{x1D709})=1$
. This definition is justified, because by our assumptions on
![]() $\mathfrak{N}$
, this sum is actually finite.
$\mathfrak{N}$
, this sum is actually finite.
Expanding in powers of
![]() $t$
defines the
$t$
defines the
![]() $\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})$
for
$\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})$
for
![]() $k\geqslant 0$
:
$k\geqslant 0$
:
For example,
![]() $\unicode[STIX]{x1D700}_{0}=1$
, and
$\unicode[STIX]{x1D700}_{0}=1$
, and
In general,
Corollary 3.16. For every
![]() $k\geqslant 0$
, we have
$k\geqslant 0$
, we have
![]() $\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})\in K^{{\leqslant}k}(\mathfrak{M})$
. Hence,
$\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})\in K^{{\leqslant}k}(\mathfrak{M})$
. Hence,
![]() $\unicode[STIX]{x1D700}_{t}(\unicode[STIX]{x1D709})\in \mathscr{K}(\mathfrak{M})$
. In particular,
$\unicode[STIX]{x1D700}_{t}(\unicode[STIX]{x1D709})\in \mathscr{K}(\mathfrak{M})$
. In particular,
![]() $\unicode[STIX]{x1D700}_{1}(\unicode[STIX]{x1D709})$
is virtually indecomposable for all
$\unicode[STIX]{x1D700}_{1}(\unicode[STIX]{x1D709})$
is virtually indecomposable for all
![]() $\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
.
$\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
.
Proof. It suffices to prove that
![]() $E_{k}(\unicode[STIX]{x1D700}_{t}(\unicode[STIX]{x1D709}))\equiv 0~\text{mod}~(t^{k})$
for all
$E_{k}(\unicode[STIX]{x1D700}_{t}(\unicode[STIX]{x1D709}))\equiv 0~\text{mod}~(t^{k})$
for all
![]() $k$
. In fact,
$k$
. In fact,

is, indeed, divisible by
![]() $t^{k}$
, if all
$t^{k}$
, if all
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}$
are positive.◻
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}$
are positive.◻
Remark 3.17. The operator
![]() $F_{n}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
respects strict algebroids. The same is true for all
$F_{n}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
respects strict algebroids. The same is true for all
![]() $\unicode[STIX]{x1D700}_{k}$
.
$\unicode[STIX]{x1D700}_{k}$
.
Epsilons as logarithms
Suppose there exists an abelian group
![]() $\unicode[STIX]{x1D6E4}$
and a decomposition of
$\unicode[STIX]{x1D6E4}$
and a decomposition of
![]() $\mathfrak{M}$
(as an algebroid, not a linear stack) into a disjoint union
$\mathfrak{M}$
(as an algebroid, not a linear stack) into a disjoint union
We require that if
![]() $\mathfrak{E}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}$
is defined by the cartesian diagram
$\mathfrak{E}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}$
is defined by the cartesian diagram

then the composition
factors through
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}}\subset \mathfrak{M}$
.
$\mathfrak{M}_{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}}\subset \mathfrak{M}$
.
We call such
![]() $\unicode[STIX]{x1D6E4}$
a grading group for
$\unicode[STIX]{x1D6E4}$
a grading group for
![]() $\mathfrak{M}$
.
$\mathfrak{M}$
.
The grading group
![]() $\unicode[STIX]{x1D6E4}$
decomposes
$\unicode[STIX]{x1D6E4}$
decomposes
![]() $K(\mathfrak{M})$
into a direct sum
$K(\mathfrak{M})$
into a direct sum
where
![]() $K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
is the submodule of
$K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
is the submodule of
![]() $K(\mathfrak{M})$
generated by stack functions
$K(\mathfrak{M})$
generated by stack functions
![]() $X\rightarrow \mathfrak{M}$
that factor through
$X\rightarrow \mathfrak{M}$
that factor through
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
. The Hall product, as well as the commutative product, are graded with respect to (31). For
$\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
. The Hall product, as well as the commutative product, are graded with respect to (31). For
![]() $x\in K(\mathfrak{M})$
, we denote the projection of
$x\in K(\mathfrak{M})$
, we denote the projection of
![]() $x$
into the component
$x$
into the component
![]() $K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
by
$K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
by
![]() $x_{\unicode[STIX]{x1D6FE}}$
.
$x_{\unicode[STIX]{x1D6FE}}$
.
Let
![]() $\mathfrak{N}\subset \mathfrak{M}$
be a linear algebraic substack avoiding
$\mathfrak{N}\subset \mathfrak{M}$
be a linear algebraic substack avoiding
![]() $\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
, with the properties:
$\operatorname{Spec}R\stackrel{0}{\longrightarrow }\mathfrak{M}$
, with the properties:
(i) every intersection
 $\mathfrak{N}_{\unicode[STIX]{x1D6FE}}=\mathfrak{N}\cap \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
is of finite type;
$\mathfrak{N}_{\unicode[STIX]{x1D6FE}}=\mathfrak{N}\cap \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
is of finite type;(ii)
 $\mathfrak{N}$
is closed under direct summands and extensions in
$\mathfrak{N}$
is closed under direct summands and extensions in
 $\mathfrak{M}$
, the latter meaning that if
$\mathfrak{M}$
, the latter meaning that if
 $\mathfrak{N}^{(2)}$
is defined as in (29), then the composition
$\mathfrak{N}^{(2)}$
is defined as in (29), then the composition
 $\mathfrak{N}^{(2)}\rightarrow \mathfrak{M}^{(2)}\stackrel{b}{\longrightarrow }\mathfrak{M}$
factors through
$\mathfrak{N}^{(2)}\rightarrow \mathfrak{M}^{(2)}\stackrel{b}{\longrightarrow }\mathfrak{M}$
factors through
 $\mathfrak{N}\subset \mathfrak{M}$
;
$\mathfrak{N}\subset \mathfrak{M}$
;(iii) there is a submonoid
 $\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
such that
 $\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\not =\varnothing$
implies that
$\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\not =\varnothing$
implies that
 $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
. The monoid
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
. The monoid
 $\unicode[STIX]{x1D6E4}_{+}$
is required to have the property that every
$\unicode[STIX]{x1D6E4}_{+}$
is required to have the property that every
 $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
admits only finitely many decompositions
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
admits only finitely many decompositions
 $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
such that both
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
such that both
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
. We will further assume that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
. We will further assume that
 $\unicode[STIX]{x1D6E4}_{+}$
has the property that the intersection of all cofinite ideals is empty.
$\unicode[STIX]{x1D6E4}_{+}$
has the property that the intersection of all cofinite ideals is empty.
If these axioms hold,
![]() $\mathfrak{N}$
satisfies the finiteness conditions above, so that the
$\mathfrak{N}$
satisfies the finiteness conditions above, so that the
![]() $\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})$
are defined for all
$\unicode[STIX]{x1D700}_{k}(\unicode[STIX]{x1D709})$
are defined for all
![]() $\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
.
$\unicode[STIX]{x1D709}\in K(\mathfrak{M})$
.
Remark 3.18. If
![]() $\mathfrak{M}$
is the stack of coherent sheaves on a projective curve, then we can take
$\mathfrak{M}$
is the stack of coherent sheaves on a projective curve, then we can take
![]() $\unicode[STIX]{x1D6E4}=\mathbb{Z}^{2}$
and define
$\unicode[STIX]{x1D6E4}=\mathbb{Z}^{2}$
and define
![]() $\mathfrak{M}_{(d,r)}$
, for
$\mathfrak{M}_{(d,r)}$
, for
![]() $(d,r)\in \mathbb{Z}^{2}$
to be the stack of sheaves of rank
$(d,r)\in \mathbb{Z}^{2}$
to be the stack of sheaves of rank
![]() $r$
and degree
$r$
and degree
![]() $d$
. Suppose
$d$
. Suppose
![]() $\mathfrak{N}$
is the stack of bundles whose Harder–Narasimhan slopes are contained in the interval
$\mathfrak{N}$
is the stack of bundles whose Harder–Narasimhan slopes are contained in the interval
![]() $(a,b)\subset \mathbb{R}$
. Then we can take
$(a,b)\subset \mathbb{R}$
. Then we can take
and the above requirements will be satisfied.
Remark 3.19. If
![]() $\mathfrak{M}$
is the stack of representations of a quiver
$\mathfrak{M}$
is the stack of representations of a quiver
![]() $Q$
, we can take
$Q$
, we can take
![]() $\unicode[STIX]{x1D6E4}=\mathbb{Z}^{Q_{0}}$
, where
$\unicode[STIX]{x1D6E4}=\mathbb{Z}^{Q_{0}}$
, where
![]() $Q_{0}$
is the set of vertices of
$Q_{0}$
is the set of vertices of
![]() $Q$
, and then set
$Q$
, and then set
![]() $\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
, for
$\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
, for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, equal to the stack of representations with dimension vector
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, equal to the stack of representations with dimension vector
![]() $\unicode[STIX]{x1D6FE}$
. If we take
$\unicode[STIX]{x1D6FE}$
. If we take
![]() $\mathfrak{N}=\mathfrak{M}_{\ast }$
, we can take
$\mathfrak{N}=\mathfrak{M}_{\ast }$
, we can take
![]() $\unicode[STIX]{x1D6E4}_{+}=\mathbb{Z}_{{\geqslant}0}^{Q_{0}}$
.
$\unicode[STIX]{x1D6E4}_{+}=\mathbb{Z}_{{\geqslant}0}^{Q_{0}}$
.
Let us also define
for any cofinite ideal
![]() $S\subset \unicode[STIX]{x1D6E4}_{+}$
. For every such
$S\subset \unicode[STIX]{x1D6E4}_{+}$
. For every such
![]() $S$
, the group
$S$
, the group
![]() $K(\mathfrak{M})_{S}$
is an ideal (with respect to both multiplications) in the ring
$K(\mathfrak{M})_{S}$
is an ideal (with respect to both multiplications) in the ring
![]() $K(\mathfrak{M})_{+}=K(\mathfrak{M})_{\unicode[STIX]{x1D6E4}_{+}}$
, and we may complete
$K(\mathfrak{M})_{+}=K(\mathfrak{M})_{\unicode[STIX]{x1D6E4}_{+}}$
, and we may complete
![]() $K(\mathfrak{M})_{+}$
with respect to this collection of ideals to obtain
$K(\mathfrak{M})_{+}$
with respect to this collection of ideals to obtain
![]() $\hat{K}(\mathfrak{M})_{+}$
. The morphism
$\hat{K}(\mathfrak{M})_{+}$
. The morphism
![]() $K(\mathfrak{M})_{+}\rightarrow \hat{K}(\mathfrak{M})_{+}$
is injective and both multiplications extend to
$K(\mathfrak{M})_{+}\rightarrow \hat{K}(\mathfrak{M})_{+}$
is injective and both multiplications extend to
![]() $\hat{K}(\mathfrak{M})_{+}$
.
$\hat{K}(\mathfrak{M})_{+}$
.
In
![]() $\hat{K}(\mathfrak{M})_{+}$
, the sum
$\hat{K}(\mathfrak{M})_{+}$
, the sum
converges.
The idempotent operators commute with the
![]() $\unicode[STIX]{x1D6E4}$
-grading, and so everything defined in terms of them does too. In particular,
$\unicode[STIX]{x1D6E4}$
-grading, and so everything defined in terms of them does too. In particular,
![]() $\hat{K}(\mathfrak{M})_{+}$
is a graded Poisson algebra, and the Lie algebra of degree +1 elements in
$\hat{K}(\mathfrak{M})_{+}$
is a graded Poisson algebra, and the Lie algebra of degree +1 elements in
![]() $\hat{K}(\mathfrak{M})_{+}$
, which we will denote
$\hat{K}(\mathfrak{M})_{+}$
, which we will denote
![]() $\hat{K}^{\text{vir}}(\mathfrak{M})_{+}$
, is equal to the completion of
$\hat{K}^{\text{vir}}(\mathfrak{M})_{+}$
, is equal to the completion of
![]() $K^{\text{vir}}(\mathfrak{M})_{+}=\bigoplus _{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}}K^{\text{vir}}(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
.
$K^{\text{vir}}(\mathfrak{M})_{+}=\bigoplus _{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}}K^{\text{vir}}(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
.
Proposition 3.20. In
![]() $\hat{K}(\mathfrak{M})_{+}[[t]]$
, we have
$\hat{K}(\mathfrak{M})_{+}[[t]]$
, we have
Hence, we can write
where exponential and logarithm are defined by their power series using the Hall product. In particular,
and
Proof. Using the formula
the result follows. ◻
Remark 3.21. Compare the two formulas
Remark 3.22. Let us write
![]() $\hat{\mathscr{K}}(\mathfrak{M})_{+}$
for the subspace of
$\hat{\mathscr{K}}(\mathfrak{M})_{+}$
for the subspace of
![]() $\hat{K}(\mathfrak{M})_{+}[[t]]$
defined by requiring the coefficient of
$\hat{K}(\mathfrak{M})_{+}[[t]]$
defined by requiring the coefficient of
![]() $t^{k}$
to be contained in
$t^{k}$
to be contained in
![]() $\hat{K}^{{\leqslant}k}(\mathfrak{M})_{+}$
, for all
$\hat{K}^{{\leqslant}k}(\mathfrak{M})_{+}$
, for all
![]() $k$
. Then
$k$
. Then
Remark 3.23. Setting
![]() $t=1$
, we also get that
$t=1$
, we also get that
![]() $1+[\mathfrak{N}]=\exp _{\ast }(\unicode[STIX]{x1D700}_{1}[\mathfrak{N}])$
. One should think of
$1+[\mathfrak{N}]=\exp _{\ast }(\unicode[STIX]{x1D700}_{1}[\mathfrak{N}])$
. One should think of
![]() $1+[\mathfrak{N}]$
as group-like.
$1+[\mathfrak{N}]$
as group-like.
Hopf algebra
We make a brief remark, without striving for generality.
Let us fix
![]() $\mathfrak{N}\subset \mathfrak{M}$
and
$\mathfrak{N}\subset \mathfrak{M}$
and
![]() $\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
as before. Assume for simplicity that
$\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
as before. Assume for simplicity that
![]() $\unicode[STIX]{x1D6E4}$
is free. In particular,
$\unicode[STIX]{x1D6E4}$
is free. In particular,
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=0$
, for
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=0$
, for
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
, implies
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
, implies
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=0$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}=0$
.
For
![]() $0\not =\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
, abbreviate the element
$0\not =\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
, abbreviate the element
![]() $[\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\rightarrow \mathfrak{M}]\in K(\mathfrak{M})$
by
$[\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\rightarrow \mathfrak{M}]\in K(\mathfrak{M})$
by
![]() $[\unicode[STIX]{x1D6FE}]$
.
$[\unicode[STIX]{x1D6FE}]$
.
For a finite sequence
![]() $(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}$
of non-zero elements of
$(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}$
of non-zero elements of
![]() $\unicode[STIX]{x1D6E4}_{+}$
, write
$\unicode[STIX]{x1D6E4}_{+}$
, write
In particular, for
![]() $n=0$
, we have
$n=0$
, we have
![]() $[\varnothing ]=1$
.
$[\varnothing ]=1$
.
In many cases of interest, the Hall algebra elements
![]() $[(\unicode[STIX]{x1D6FE})]$
, as
$[(\unicode[STIX]{x1D6FE})]$
, as
![]() $(\unicode[STIX]{x1D6FE})$
runs over all finite sequences of non-zero elements of
$(\unicode[STIX]{x1D6FE})$
runs over all finite sequences of non-zero elements of
![]() $\unicode[STIX]{x1D6E4}_{+}$
, are linearly independent over
$\unicode[STIX]{x1D6E4}_{+}$
, are linearly independent over
![]() $\mathbb{Q}$
. Let us assume that this is the case. Then the
$\mathbb{Q}$
. Let us assume that this is the case. Then the
![]() $\mathbb{Q}$
-span of all
$\mathbb{Q}$
-span of all
![]() $[(\unicode[STIX]{x1D6FE})]$
is a
$[(\unicode[STIX]{x1D6FE})]$
is a
![]() $\mathbb{Q}$
-subalgebra of
$\mathbb{Q}$
-subalgebra of
![]() $K(\mathfrak{M})$
that is free on the generators
$K(\mathfrak{M})$
that is free on the generators
![]() $[\unicode[STIX]{x1D6FE}]$
, for
$[\unicode[STIX]{x1D6FE}]$
, for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
, as a unitary
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
, as a unitary
![]() $\mathbb{Q}$
-algebra. Let us denote this algebra by
$\mathbb{Q}$
-algebra. Let us denote this algebra by
![]() $U$
. Let us further assume that the morphism induced by the commutative product
$U$
. Let us further assume that the morphism induced by the commutative product
![]() $U\otimes U\rightarrow K(\mathfrak{M})$
is injective. (Again, this will hold in many cases of interest.)
$U\otimes U\rightarrow K(\mathfrak{M})$
is injective. (Again, this will hold in many cases of interest.)
We will now define a comultiplication
![]() $\unicode[STIX]{x1D6E5}$
on
$\unicode[STIX]{x1D6E5}$
on
![]() $U$
, making a
$U$
, making a
![]() $U$
a cocommutative Hopf algebra over
$U$
a cocommutative Hopf algebra over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
To define
![]() $\unicode[STIX]{x1D6E5}$
, it is convenient to extend the notation
$\unicode[STIX]{x1D6E5}$
, it is convenient to extend the notation
![]() $[(\unicode[STIX]{x1D6FE})]$
to finite sequences of elements of
$[(\unicode[STIX]{x1D6FE})]$
to finite sequences of elements of
![]() $\unicode[STIX]{x1D6E4}_{+}$
, which may be zero. This is done by setting
$\unicode[STIX]{x1D6E4}_{+}$
, which may be zero. This is done by setting
![]() $[0]=1$
. Thus,
$[0]=1$
. Thus,
![]() $[(\unicode[STIX]{x1D6FE})]$
is unchanged by ‘crossing off its zeros’. We then define
$[(\unicode[STIX]{x1D6FE})]$
is unchanged by ‘crossing off its zeros’. We then define
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}:U & \longrightarrow & \displaystyle U\otimes U\nonumber\\ \displaystyle \hspace{0.0pt}[(\unicode[STIX]{x1D6FE})] & \longmapsto & \displaystyle \mathop{\sum }_{(\unicode[STIX]{x1D6FC})+(\unicode[STIX]{x1D6FD})=(\unicode[STIX]{x1D6FE})}[(\unicode[STIX]{x1D6FC})]\otimes [(\unicode[STIX]{x1D6FD})],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}:U & \longrightarrow & \displaystyle U\otimes U\nonumber\\ \displaystyle \hspace{0.0pt}[(\unicode[STIX]{x1D6FE})] & \longmapsto & \displaystyle \mathop{\sum }_{(\unicode[STIX]{x1D6FC})+(\unicode[STIX]{x1D6FD})=(\unicode[STIX]{x1D6FE})}[(\unicode[STIX]{x1D6FC})]\otimes [(\unicode[STIX]{x1D6FD})],\nonumber\end{eqnarray}$$
where the sum is over all pairs of sequences of the same length as
![]() $\unicode[STIX]{x1D6FE}$
, but allowing zeros.
$\unicode[STIX]{x1D6FE}$
, but allowing zeros.
This defines on
![]() $U$
the structure of a cocommutative Hopf algebra.
$U$
the structure of a cocommutative Hopf algebra.
Lemma 3.24. The diagram
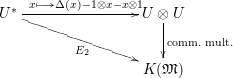
is commutative, where
![]() $U^{\ast }\subset U$
is the augmentation ideal.
$U^{\ast }\subset U$
is the augmentation ideal.
It follows that the virtual indecomposables in
![]() $U$
are equal to the primitives with respect to the Hopf algebra structure:
$U$
are equal to the primitives with respect to the Hopf algebra structure:
As
![]() $U$
is a cocommutative Hopf algebra, it is isomorphic to the universal enveloping algebra of
$U$
is a cocommutative Hopf algebra, it is isomorphic to the universal enveloping algebra of
![]() $U^{\text{prim}}$
, by the Cartier–Gabriel theorem [Reference CartierCar07, Theorem 3.8.2].
$U^{\text{prim}}$
, by the Cartier–Gabriel theorem [Reference CartierCar07, Theorem 3.8.2].
The Lie algebra
![]() $U^{\text{vir}}$
is free, as a Lie algebra over
$U^{\text{vir}}$
is free, as a Lie algebra over
![]() $\mathbb{Q}$
, on the elements
$\mathbb{Q}$
, on the elements
 $$\begin{eqnarray}\unicode[STIX]{x1D700}[\unicode[STIX]{x1D6FE}]=\mathop{\sum }_{n>0}\frac{(-1)^{n+1}}{n}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{n} \\ \unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}>0}}[\unicode[STIX]{x1D6FE}_{1}]\ast \cdots \ast [\unicode[STIX]{x1D6FE}_{n}],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}[\unicode[STIX]{x1D6FE}]=\mathop{\sum }_{n>0}\frac{(-1)^{n+1}}{n}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{1}+\cdots +\unicode[STIX]{x1D6FE}_{n} \\ \unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{n}>0}}[\unicode[STIX]{x1D6FE}_{1}]\ast \cdots \ast [\unicode[STIX]{x1D6FE}_{n}],\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}\setminus \{0\}$
.
Remark 3.25. Suppose
![]() $\mathfrak{N}=\mathfrak{M}=\mathfrak{Vect}$
is the stack of vector bundles. We take
$\mathfrak{N}=\mathfrak{M}=\mathfrak{Vect}$
is the stack of vector bundles. We take
![]() $\unicode[STIX]{x1D6E4}=\mathbb{Z}$
and
$\unicode[STIX]{x1D6E4}=\mathbb{Z}$
and
![]() $\unicode[STIX]{x1D6E4}_{+}=\mathbb{Z}_{{\geqslant}0}$
. Then the
$\unicode[STIX]{x1D6E4}_{+}=\mathbb{Z}_{{\geqslant}0}$
. Then the
![]() $[(\unicode[STIX]{x1D6FE})]$
are, indeed, linearly independent over
$[(\unicode[STIX]{x1D6FE})]$
are, indeed, linearly independent over
![]() $\mathbb{Q}$
, at least if our ground ring
$\mathbb{Q}$
, at least if our ground ring
![]() $R$
is a field. Moreover,
$R$
is a field. Moreover,
![]() $U\otimes \,U\rightarrow K(\mathfrak{M})$
is injective. The Hopf algebra we obtain is the Hopf algebra of non-commutative symmetric functions, see [Reference CartierCar07, Example 4.1 (F)].
$U\otimes \,U\rightarrow K(\mathfrak{M})$
is injective. The Hopf algebra we obtain is the Hopf algebra of non-commutative symmetric functions, see [Reference CartierCar07, Example 4.1 (F)].
Remark 3.26. It is doubtful that it is possible to extend the coproduct to all of
![]() $K(\mathfrak{M})$
in such a way that
$K(\mathfrak{M})$
in such a way that
![]() $K^{\text{vir}}(\mathfrak{M})=K(\mathfrak{M})^{\text{prim}}$
. By the above considerations, we consider the family of operators
$K^{\text{vir}}(\mathfrak{M})=K(\mathfrak{M})^{\text{prim}}$
. By the above considerations, we consider the family of operators
![]() $(E_{n})$
as a substitute, which allows us to prove at least some of the result one would expect in a cocommutative Hopf algebra. In particular, we find it unlikely that, in general,
$(E_{n})$
as a substitute, which allows us to prove at least some of the result one would expect in a cocommutative Hopf algebra. In particular, we find it unlikely that, in general,
![]() $K(\mathfrak{M})$
would be isomorphic to the universal enveloping algebra of
$K(\mathfrak{M})$
would be isomorphic to the universal enveloping algebra of
![]() $K^{\text{vir}}(\mathfrak{M})$
.
$K^{\text{vir}}(\mathfrak{M})$
.
4 Integration
The integral of a stack function
![]() $(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
does three things: it forgets the structure map to
$(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
does three things: it forgets the structure map to
![]() $(\mathfrak{M},\mathfrak{A})$
, it forgets the algebroid structure, mapping
$(\mathfrak{M},\mathfrak{A})$
, it forgets the algebroid structure, mapping
![]() $(X,A)$
to
$(X,A)$
to
![]() $X$
, and it introduces the bundle relations in
$X$
, and it introduces the bundle relations in
![]() $K(\text{St})$
, for non-inert bundles of algebraic stacks.
$K(\text{St})$
, for non-inert bundles of algebraic stacks.
The vector bundle relations
Let
![]() $K(\text{St})$
be the Grothendieck
$K(\text{St})$
be the Grothendieck
![]() $K(\text{DM})$
-algebra of algebraic stacks (finite type, with affine diagonal), modulo the scissor and the bundle relations. A bundle relation is any equation of the form
$K(\text{DM})$
-algebra of algebraic stacks (finite type, with affine diagonal), modulo the scissor and the bundle relations. A bundle relation is any equation of the form
for a fibre bundle
![]() $Y\rightarrow X$
of algebraic stacks with special structure group and fibre
$Y\rightarrow X$
of algebraic stacks with special structure group and fibre
![]() $F$
.
$F$
.
It is well known that
A proof can be found, for example in [Reference BridgelandBri12]. Along the same lines, one proves that
Note that the (connected, semi-simple) inertia operator does not preserve non-inert bundle relations. Therefore, in
![]() $K(\text{St})$
, we cannot talk about
$K(\text{St})$
, we cannot talk about
![]() $I^{\circ ,\text{ss}}[X]$
, only about
$I^{\circ ,\text{ss}}[X]$
, only about
![]() $[I_{X}^{\circ ,\text{ss}}]$
.
$[I_{X}^{\circ ,\text{ss}}]$
.
Regular motivic weights
Definition 4.1. We say an element of
![]() $K(\text{St})$
is regular if it can be written with a denominator which does not vanish at
$K(\text{St})$
is regular if it can be written with a denominator which does not vanish at
![]() $q=1$
. Thus, the subalgebra of regular motivic weights
$q=1$
. Thus, the subalgebra of regular motivic weights
![]() $K(\text{St})_{\text{reg}}\subset K(\text{St})$
is by definition the image of the morphism of
$K(\text{St})_{\text{reg}}\subset K(\text{St})$
is by definition the image of the morphism of
![]() $K(\text{Var})$
-algebras:
$K(\text{Var})$
-algebras:
The image of
![]() $K(\text{DM})$
in
$K(\text{DM})$
in
![]() $K(\text{St})$
is contained in
$K(\text{St})$
is contained in
![]() $K(\text{St})_{\text{reg}}$
. Hence, we can also think of
$K(\text{St})_{\text{reg}}$
. Hence, we can also think of
![]() $K(\text{St})_{\text{reg}}$
as a
$K(\text{St})_{\text{reg}}$
as a
![]() $K(\text{DM})$
-algebra. This follows from the following lemma.
$K(\text{DM})$
-algebra. This follows from the following lemma.
Lemma 4.2. Every finite type stack with quasi-finite stabilizer has regular motivic weight in
![]() $K(\text{St})$
.
$K(\text{St})$
.
Proof. Let
![]() $Z$
be a stack with quasi-finite stabilizer (meaning that its inertia
$Z$
be a stack with quasi-finite stabilizer (meaning that its inertia
![]() $I_{Z}$
is quasi-finite over
$I_{Z}$
is quasi-finite over
![]() $Z$
). By stratifying
$Z$
). By stratifying
![]() $Z$
, if necessary, we may assume that the inertia stack of
$Z$
, if necessary, we may assume that the inertia stack of
![]() $Z$
is in fact finite. By [Reference KreschKre99, Proposition 3.5.7],
$Z$
is in fact finite. By [Reference KreschKre99, Proposition 3.5.7],
![]() $Z$
is stratified by global quotient stacks, so we may assume that
$Z$
is stratified by global quotient stacks, so we may assume that
![]() $Z=Y/\!\operatorname{GL}_{m}$
, for an algebraic space
$Z=Y/\!\operatorname{GL}_{m}$
, for an algebraic space
![]() $Y$
, such that
$Y$
, such that
![]() $\operatorname{GL}_{m}$
acts on
$\operatorname{GL}_{m}$
acts on
![]() $Y$
with finite stabilizer. The maximal torus
$Y$
with finite stabilizer. The maximal torus
![]() $T\subset \operatorname{GL}_{m}$
then also acts with finite stabilizer on
$T\subset \operatorname{GL}_{m}$
then also acts with finite stabilizer on
![]() $Y$
. The flattening stratification
$Y$
. The flattening stratification
![]() $\coprod Y_{i}\rightarrow Y$
of the stabilizer
$\coprod Y_{i}\rightarrow Y$
of the stabilizer
![]() $\operatorname{Stab}_{T}Y$
is then
$\operatorname{Stab}_{T}Y$
is then
![]() $T$
-equivariant, so that
$T$
-equivariant, so that
![]() $T$
acts on each
$T$
acts on each
![]() $Y_{i}$
, and by passing to open and closed subspaces of the
$Y_{i}$
, and by passing to open and closed subspaces of the
![]() $Y_{i}$
, we may assume that the action of
$Y_{i}$
, we may assume that the action of
![]() $T$
on
$T$
on
![]() $Y_{i}$
has constant stabilizer (see [Reference OesterléOes14, I, 5.4]). Then
$Y_{i}$
has constant stabilizer (see [Reference OesterléOes14, I, 5.4]). Then
![]() $T$
acts on
$T$
acts on
![]() $Y_{i}$
freely through a quotient
$Y_{i}$
freely through a quotient
![]() $T_{i}$
by a finite subgroup. We conclude
$T_{i}$
by a finite subgroup. We conclude
because each quotient
![]() $T_{i}$
of
$T_{i}$
of
![]() $T$
is isomorphic to
$T$
is isomorphic to
![]() $T$
. The last term in (32) is regular, because each
$T$
. The last term in (32) is regular, because each
![]() $Y_{i}/T_{i}$
is an algebraic space, and
$Y_{i}/T_{i}$
is an algebraic space, and
does not vanish at
![]() $q=1$
.◻
$q=1$
.◻
The integral
Mapping a stack function
![]() $(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
to the class
$(X,A)\rightarrow (\mathfrak{M},\mathfrak{A})$
to the class
![]() $[X]\in K(\text{St})$
gives rise to a well-defined homomorphism
$[X]\in K(\text{St})$
gives rise to a well-defined homomorphism
![]() $K(\mathfrak{M})\rightarrow K(\text{St})$
of
$K(\mathfrak{M})\rightarrow K(\text{St})$
of
![]() $K(\text{DM})$
-modules. We denote this homomorphism by
$K(\text{DM})$
-modules. We denote this homomorphism by
4.1 The ‘no poles’ theorem
Theorem 4.3. The composition
![]() $\int \circ \,I^{\circ ,\text{ss}}$
factors through the algebra of regular motivic weights.
$\int \circ \,I^{\circ ,\text{ss}}$
factors through the algebra of regular motivic weights.

Proof. It suffices to prove that
![]() $[A^{\times ,\text{ss}}]\in K(\text{St})$
is regular for every clear algebroid
$[A^{\times ,\text{ss}}]\in K(\text{St})$
is regular for every clear algebroid
![]() $(X,A)$
admitting a faithful representation. This will suffice, by Proposition 1.66. If
$(X,A)$
admitting a faithful representation. This will suffice, by Proposition 1.66. If
![]() $(X,A)$
is such an algebroid, there exists a Deligne–Mumford stack
$(X,A)$
is such an algebroid, there exists a Deligne–Mumford stack
![]() $Y$
with a left
$Y$
with a left
![]() $\operatorname{GL}_{n}$
-action together with a strict
$\operatorname{GL}_{n}$
-action together with a strict
![]() $\operatorname{GL}_{n}$
-equivariant algebra subbundle
$\operatorname{GL}_{n}$
-equivariant algebra subbundle
![]() $B{\hookrightarrow}M_{n\times n}|_{Y}$
such that
$B{\hookrightarrow}M_{n\times n}|_{Y}$
such that
![]() $B^{\times }=\operatorname{Stab}_{\operatorname{GL}_{n}}Y$
and
$B^{\times }=\operatorname{Stab}_{\operatorname{GL}_{n}}Y$
and
![]() $(X,A)=(\operatorname{GL}_{n}\backslash Y,\operatorname{GL}_{n}\backslash B)$
.
$(X,A)=(\operatorname{GL}_{n}\backslash Y,\operatorname{GL}_{n}\backslash B)$
.
Let
![]() $D_{n}\subset M_{n\times n}$
be the diagonal subalgebra and
$D_{n}\subset M_{n\times n}$
be the diagonal subalgebra and
![]() $T=D_{n}^{\times }$
the standard maximal torus of
$T=D_{n}^{\times }$
the standard maximal torus of
![]() $\operatorname{GL}_{n}$
. As
$\operatorname{GL}_{n}$
. As
![]() $\operatorname{GL}_{n}$
acts on
$\operatorname{GL}_{n}$
acts on
![]() $B\subset M_{n\times n}|_{Y}$
, so does the torus
$B\subset M_{n\times n}|_{Y}$
, so does the torus
![]() $T$
. We will now stratify
$T$
. We will now stratify
![]() $B$
by the stabilizer with respect to the action of
$B$
by the stabilizer with respect to the action of
![]() $T$
. For this stratification to be canonical, we need
$T$
. For this stratification to be canonical, we need
![]() $\operatorname{Stab}_{T}B$
to be the units in a finite type algebra over
$\operatorname{Stab}_{T}B$
to be the units in a finite type algebra over
![]() $B$
.
$B$
.
In fact, such an algebra
![]() $C\subset D_{n}|_{B}$
is given as the intersection of
$C\subset D_{n}|_{B}$
is given as the intersection of
![]() $D_{n}|_{B}$
with
$D_{n}|_{B}$
with
![]() $(B|_{B})^{\text{fix}}$
inside
$(B|_{B})^{\text{fix}}$
inside
![]() $M_{n\times n}|_{B}$
. Here,
$M_{n\times n}|_{B}$
. Here,
![]() $(B|_{B})^{\text{fix}}$
is the centralizer of the tautological section of
$(B|_{B})^{\text{fix}}$
is the centralizer of the tautological section of
![]() $B|_{B}$
, or, under the identification
$B|_{B}$
, or, under the identification
![]() $B|_{B}=B\times _{Y}B$
, the stack of commuting pairs. Thus, a section
$B|_{B}=B\times _{Y}B$
, the stack of commuting pairs. Thus, a section
![]() $(u,b,y)\in D_{n}|_{B}$
is in
$(u,b,y)\in D_{n}|_{B}$
is in
![]() $C$
if and only if
$C$
if and only if
![]() $u\in Z_{B(y)}(b)$
.
$u\in Z_{B(y)}(b)$
.
We have, indeed, an equality
of relative group schemes over
![]() $B$
, because for
$B$
, because for
![]() $t\in T$
and
$t\in T$
and
![]() $(b,y)\in B\subset M_{n\times n}|_{Y}$
,
$(b,y)\in B\subset M_{n\times n}|_{Y}$
,
 $$\begin{eqnarray}\displaystyle t\in \operatorname{Stab}_{T}(b,y) & \Longleftrightarrow & \displaystyle \text{}^{t}b=b\text{ and }ty=y\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle tb=bt\text{ and }t\in \operatorname{Stab}_{\operatorname{GL}_{n}(y)}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle tb=bt\text{ and }t\in B^{\times }(y)\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle t\in Z_{B^{\times }(y)}(b)\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle t\in C^{\times }(b,y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle t\in \operatorname{Stab}_{T}(b,y) & \Longleftrightarrow & \displaystyle \text{}^{t}b=b\text{ and }ty=y\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle tb=bt\text{ and }t\in \operatorname{Stab}_{\operatorname{GL}_{n}(y)}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle tb=bt\text{ and }t\in B^{\times }(y)\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle t\in Z_{B^{\times }(y)}(b)\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle t\in C^{\times }(b,y).\nonumber\end{eqnarray}$$
The subalgebras of
![]() $D_{n}$
are in one-to-one correspondence with partitions
$D_{n}$
are in one-to-one correspondence with partitions
![]() $I=\{I_{1},\ldots ,I_{r}\}$
of the set
$I=\{I_{1},\ldots ,I_{r}\}$
of the set
![]() $\text{}\underline{n}=\{1,\ldots ,n\}$
. The partition
$\text{}\underline{n}=\{1,\ldots ,n\}$
. The partition
![]() $\text{}\underline{n}=I_{1}\sqcup \cdots \sqcup I_{r}$
corresponds to the subalgebra
$\text{}\underline{n}=I_{1}\sqcup \cdots \sqcup I_{r}$
corresponds to the subalgebra
![]() $D_{I}$
whose primitive idempotents are the
$D_{I}$
whose primitive idempotents are the
![]() $e_{I_{\unicode[STIX]{x1D70C}}}=\sum _{i\in I_{\unicode[STIX]{x1D70C}}}e_{i}$
, for
$e_{I_{\unicode[STIX]{x1D70C}}}=\sum _{i\in I_{\unicode[STIX]{x1D70C}}}e_{i}$
, for
![]() $\unicode[STIX]{x1D70C}=1,\ldots ,r$
. Let us write
$\unicode[STIX]{x1D70C}=1,\ldots ,r$
. Let us write
![]() $T_{I}=D_{I}^{\times }$
for the torus of units in
$T_{I}=D_{I}^{\times }$
for the torus of units in
![]() $D_{I}$
.
$D_{I}$
.
Now there is a unique stratification
such that a section
![]() $(b,y)$
of
$(b,y)$
of
![]() $B$
factors through
$B$
factors through
![]() $B_{I}$
if and only if the pullback of
$B_{I}$
if and only if the pullback of
![]() $C\subset D_{n}|_{B}$
via
$C\subset D_{n}|_{B}$
via
![]() $(b,y)$
is equal to
$(b,y)$
is equal to
![]() $D_{I}$
. The existence of this stratification is proved by passing to the rank stratification (see Definition 1.23) of
$D_{I}$
. The existence of this stratification is proved by passing to the rank stratification (see Definition 1.23) of
![]() $C$
and observing that a subalgebra bundle
$C$
and observing that a subalgebra bundle
![]() $C\subset D_{n}|_{S}$
, for any stack
$C\subset D_{n}|_{S}$
, for any stack
![]() $S$
, decomposes
$S$
, decomposes
![]() $S$
into a disjoint union of open and closed substacks such that
$S$
into a disjoint union of open and closed substacks such that
![]() $C$
is constant over these components. We may reformulate the defining property of
$C$
is constant over these components. We may reformulate the defining property of
![]() $B_{I}$
by saying that
$B_{I}$
by saying that
![]() $(b,y)\in B_{I}$
if and only if
$(b,y)\in B_{I}$
if and only if
![]() $Z_{B(y)}(b)\cap D_{n}=D_{I}$
. We also have, for
$Z_{B(y)}(b)\cap D_{n}=D_{I}$
. We also have, for
![]() $(b,y)\in B_{I}$
, that
$(b,y)\in B_{I}$
, that
![]() $\operatorname{Stab}_{T}(b,y)=C^{\times }(b,y)=D_{I}^{\times }=T_{I}$
.
$\operatorname{Stab}_{T}(b,y)=C^{\times }(b,y)=D_{I}^{\times }=T_{I}$
.
The stratification (34) is
![]() $T$
-equivariant, because for
$T$
-equivariant, because for
![]() $t\in T$
and
$t\in T$
and
![]() $(b,y)\in B$
, we have
$(b,y)\in B$
, we have
 $$\begin{eqnarray}\displaystyle (b,y)\in B_{I} & \Longleftrightarrow & \displaystyle Z_{B(y)}(b)\cap D_{n}=D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle Z_{B(ty)}(\text{}^{t}b)\cap \text{}^{t}D_{n}=\text{}^{t}D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle Z_{B(ty)}(\text{}^{t}b)\cap D_{n}=D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle (\text{}^{t}b,ty)\in B_{I},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (b,y)\in B_{I} & \Longleftrightarrow & \displaystyle Z_{B(y)}(b)\cap D_{n}=D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle Z_{B(ty)}(\text{}^{t}b)\cap \text{}^{t}D_{n}=\text{}^{t}D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle Z_{B(ty)}(\text{}^{t}b)\cap D_{n}=D_{I}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle (\text{}^{t}b,ty)\in B_{I},\nonumber\end{eqnarray}$$
as
![]() $T\subset D_{n}$
and
$T\subset D_{n}$
and
![]() $D_{n}$
is commutative.
$D_{n}$
is commutative.
(Let us remark that we were not able to prove that for a general action of
![]() $T$
on a Deligne–Mumford stack
$T$
on a Deligne–Mumford stack
![]() $Y$
, the stabilizer stratifies
$Y$
, the stabilizer stratifies
![]() $Y$
equivariantly. The fact that the stabilizer is equal to the units in an algebra helps. Note also that we did not prove a defining property for (34) in terms of stabilizers in
$Y$
equivariantly. The fact that the stabilizer is equal to the units in an algebra helps. Note also that we did not prove a defining property for (34) in terms of stabilizers in
![]() $T$
.)
$T$
.)
So, for every partition
![]() $I$
of
$I$
of
![]() $\text{}\underline{n}$
, the torus
$\text{}\underline{n}$
, the torus
![]() $T$
acts on
$T$
acts on
![]() $B_{I}\subset B$
, with stabilizer
$B_{I}\subset B$
, with stabilizer
![]() $T_{I}$
. We therefore get an induced action of
$T_{I}$
. We therefore get an induced action of
![]() $T/T_{I}$
on
$T/T_{I}$
on
![]() $B_{I}$
. Matrix conjugation preserves units, so we get an induced action of
$B_{I}$
. Matrix conjugation preserves units, so we get an induced action of
![]() $T/T_{I}$
on
$T/T_{I}$
on
In fact, this action even respects
![]() $B_{I}^{\times ,\text{ss}}=B_{I}\cap B^{\times ,\text{ss}}$
, but the following modification does not.
$B_{I}^{\times ,\text{ss}}=B_{I}\cap B^{\times ,\text{ss}}$
, but the following modification does not.
Consider the action of
![]() $T_{I}\subset T$
on
$T_{I}\subset T$
on
![]() $B_{I}$
by left multiplication:
$B_{I}$
by left multiplication:
This is a well-defined action, because
![]() $t\in T_{I}$
and
$t\in T_{I}$
and
![]() $(b,y)\in B_{I}$
implies that
$(b,y)\in B_{I}$
implies that
![]() $t\in Z_{B(y)}(b)$
. In particular,
$t\in Z_{B(y)}(b)$
. In particular,
![]() $t\in B(y)$
, so that
$t\in B(y)$
, so that
![]() $(t,y)\in B$
, and the product
$(t,y)\in B$
, and the product
![]() $(t,y)(b,y)=(tb,y)$
in
$(t,y)(b,y)=(tb,y)$
in
![]() $B$
exists. Moreover,
$B$
exists. Moreover,
![]() $(tb,y)\in B_{I}$
, because
$(tb,y)\in B_{I}$
, because
![]() $Z_{B(y)}(tb)\cap D_{n}=Z_{B(y)}(b)\cap D_{n}$
. This action of
$Z_{B(y)}(tb)\cap D_{n}=Z_{B(y)}(b)\cap D_{n}$
. This action of
![]() $T_{I}$
on
$T_{I}$
on
![]() $B_{I}$
preserves
$B_{I}$
preserves
![]() $B_{I}^{\times }$
. Over fields, it also preserves sections which are semi-simple, because the product of two semi-simple commuting matrices is again a semi-simple matrix. (Note that this does not imply that
$B_{I}^{\times }$
. Over fields, it also preserves sections which are semi-simple, because the product of two semi-simple commuting matrices is again a semi-simple matrix. (Note that this does not imply that
![]() $T_{I}$
acts on
$T_{I}$
acts on
![]() $B_{I}^{\text{ss}}$
, because even if
$B_{I}^{\text{ss}}$
, because even if
![]() $(b,y)$
is a strict section of
$(b,y)$
is a strict section of
![]() $B$
, the product
$B$
, the product
![]() $(tb,y)$
may not be strict.)
$(tb,y)$
may not be strict.)
We finally consider the action of
![]() $T(I)=T_{I}\times T/T_{I}$
on
$T(I)=T_{I}\times T/T_{I}$
on
![]() $B_{I}^{\times }$
, defined by
$B_{I}^{\times }$
, defined by
The quotient stack
![]() $Z_{I}=B_{I}^{\times }/T(I)$
is a finite type scheme over
$Z_{I}=B_{I}^{\times }/T(I)$
is a finite type scheme over
![]() $R$
, so its Zariski topological space
$R$
, so its Zariski topological space
![]() $|Z_{I}|$
is a Zariski space (see [Reference Laumon and Moret-BaillyLMB00, ch. 5]). By Chevalley’s theorem (see [Reference Laumon and Moret-BaillyLMB00]), the image of
$|Z_{I}|$
is a Zariski space (see [Reference Laumon and Moret-BaillyLMB00, ch. 5]). By Chevalley’s theorem (see [Reference Laumon and Moret-BaillyLMB00]), the image of
![]() $|B_{I}^{\times ,\text{ss}}|$
in
$|B_{I}^{\times ,\text{ss}}|$
in
![]() $|Z_{I}|$
is constructible, so we can find disjoint, locally closed (reduced) algebraic substacks
$|Z_{I}|$
is constructible, so we can find disjoint, locally closed (reduced) algebraic substacks
![]() $Z_{1},\ldots ,Z_{n}\subset Z_{I}$
such that this image is equal to
$Z_{1},\ldots ,Z_{n}\subset Z_{I}$
such that this image is equal to
![]() $|Z_{1}|\sqcup \cdots \sqcup |Z_{n}|\subset |Z_{I}|$
. Let
$|Z_{1}|\sqcup \cdots \sqcup |Z_{n}|\subset |Z_{I}|$
. Let
This is a finite type algebraic stack endowed with a representable monomorphism
![]() $\widetilde{Z}_{I}\rightarrow Z_{I}$
.
$\widetilde{Z}_{I}\rightarrow Z_{I}$
.
We claim that
![]() $\widetilde{Z}_{I}$
is an algebraic stack with quasi-finite stabilizer. This will follow from the fact that, for field-valued points, the action of
$\widetilde{Z}_{I}$
is an algebraic stack with quasi-finite stabilizer. This will follow from the fact that, for field-valued points, the action of
![]() $T(I)$
on
$T(I)$
on
![]() $B_{I}^{\times ,\text{ss}}$
has finite stabilizers. To see this, assume that
$B_{I}^{\times ,\text{ss}}$
has finite stabilizers. To see this, assume that
for
![]() $(t^{\prime },t)\in T_{I}\times T/T_{I}$
and
$(t^{\prime },t)\in T_{I}\times T/T_{I}$
and
![]() $(b,y)\in B_{I}^{\times ,\text{ss}}$
. This implies that
$(b,y)\in B_{I}^{\times ,\text{ss}}$
. This implies that
![]() $ty=y$
, and hence conjugation by
$ty=y$
, and hence conjugation by
![]() $t$
preserves the fibre
$t$
preserves the fibre
![]() $B(y)$
of
$B(y)$
of
![]() $B$
over
$B$
over
![]() $y$
. We have
$y$
. We have
where
![]() $t^{\prime }$
commutes with
$t^{\prime }$
commutes with
![]() $b$
. Rewriting as
$b$
. Rewriting as
![]() $^{t}b={t^{\prime }}^{-1}b$
, we see that
$^{t}b={t^{\prime }}^{-1}b$
, we see that
![]() $^{t}b$
commutes with
$^{t}b$
commutes with
![]() $b$
. Changing basis, if necessary, we can diagonalize the three matrices
$b$
. Changing basis, if necessary, we can diagonalize the three matrices
![]() $b$
,
$b$
,
![]() $^{t}b$
, and
$^{t}b$
, and
![]() $t^{\prime }$
simultaneously. Since
$t^{\prime }$
simultaneously. Since
![]() $b$
and
$b$
and
![]() $^{t}b$
have the same eigenvalues, we see that the entries of the diagonal matrix
$^{t}b$
have the same eigenvalues, we see that the entries of the diagonal matrix
![]() $^{t}b$
are obtained from those of
$^{t}b$
are obtained from those of
![]() $b$
by a permutation. Hence, there are at most
$b$
by a permutation. Hence, there are at most
![]() $n!$
possible values for
$n!$
possible values for
![]() $^{t}b$
, and hence also for
$^{t}b$
, and hence also for
![]() $t^{\prime }=b\,^{t}b^{-1}$
. For every one of these possible values of
$t^{\prime }=b\,^{t}b^{-1}$
. For every one of these possible values of
![]() $t^{\prime }$
, there is at most one
$t^{\prime }$
, there is at most one
![]() $t\in T/T_{I}$
such that
$t\in T/T_{I}$
such that
![]() $^{t}b={t^{\prime }}^{-1}b$
. Thus, the action (35) has finite stabilizers, at least on field-valued points of
$^{t}b={t^{\prime }}^{-1}b$
. Thus, the action (35) has finite stabilizers, at least on field-valued points of
![]() $B_{I}^{\times ,\text{ss}}$
, as required.
$B_{I}^{\times ,\text{ss}}$
, as required.
Consider the cartesian diagram

obtained by pulling back
![]() $B_{I}^{\times ,\text{ss}}\rightarrow B_{I}^{\times }\rightarrow Z_{I}$
via
$B_{I}^{\times ,\text{ss}}\rightarrow B_{I}^{\times }\rightarrow Z_{I}$
via
![]() $\widetilde{Z}_{I}\rightarrow Z_{I}$
. The morphisms
$\widetilde{Z}_{I}\rightarrow Z_{I}$
. The morphisms
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are disjoint unions of isomorphisms onto locally closed substacks, so the same is true for
$\unicode[STIX]{x1D6FD}$
are disjoint unions of isomorphisms onto locally closed substacks, so the same is true for
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
and
$\unicode[STIX]{x1D6FC}^{\prime }$
and
![]() $\widetilde{\unicode[STIX]{x1D6FD}}$
. But both
$\widetilde{\unicode[STIX]{x1D6FD}}$
. But both
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
and
$\unicode[STIX]{x1D6FC}^{\prime }$
and
![]() $\widetilde{\unicode[STIX]{x1D6FD}}$
are surjective on underlying Zariski topological spaces, so by the scissor relations, we have
$\widetilde{\unicode[STIX]{x1D6FD}}$
are surjective on underlying Zariski topological spaces, so by the scissor relations, we have
in
![]() $K(\text{St})$
. The morphism
$K(\text{St})$
. The morphism
![]() $\unicode[STIX]{x1D70B}$
is a principal
$\unicode[STIX]{x1D70B}$
is a principal
![]() $T(I)$
-bundle, so the same is true for
$T(I)$
-bundle, so the same is true for
![]() $\widetilde{\unicode[STIX]{x1D70B}}$
, and so by the bundle relations, we have
$\widetilde{\unicode[STIX]{x1D70B}}$
, and so by the bundle relations, we have
in
![]() $K(\text{St})$
. It follows that we have
$K(\text{St})$
. It follows that we have
 $$\begin{eqnarray}\displaystyle [A^{\times ,\text{ss}}]\hspace{-0.3pt}=\hspace{-0.3pt}[\operatorname{GL}_{n}\backslash B^{\times ,\text{ss}}]\hspace{-0.3pt}=\hspace{-0.3pt}\frac{[B^{\times ,\text{ss}}]}{[\operatorname{GL}_{n}]} & \hspace{-0.3pt}=\hspace{-0.3pt} & \displaystyle \frac{1}{[\operatorname{GL}_{n}]}\mathop{\sum }_{I}[B_{I}^{\times ,\text{ss}}]\nonumber\\ \displaystyle & \hspace{-0.3pt}=\hspace{-0.3pt} & \displaystyle \frac{1}{[\operatorname{GL}_{n}]}\mathop{\sum }_{I}(q-1)^{n}[\widetilde{Z}_{I}]\hspace{-0.3pt}=\hspace{-0.3pt}q^{-(1/2)n(n-1)}\mathop{\prod }_{i=1}^{n-1}\frac{1}{q^{i}+\cdots +1}\mathop{\sum }_{I}[\widetilde{Z}_{I}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [A^{\times ,\text{ss}}]\hspace{-0.3pt}=\hspace{-0.3pt}[\operatorname{GL}_{n}\backslash B^{\times ,\text{ss}}]\hspace{-0.3pt}=\hspace{-0.3pt}\frac{[B^{\times ,\text{ss}}]}{[\operatorname{GL}_{n}]} & \hspace{-0.3pt}=\hspace{-0.3pt} & \displaystyle \frac{1}{[\operatorname{GL}_{n}]}\mathop{\sum }_{I}[B_{I}^{\times ,\text{ss}}]\nonumber\\ \displaystyle & \hspace{-0.3pt}=\hspace{-0.3pt} & \displaystyle \frac{1}{[\operatorname{GL}_{n}]}\mathop{\sum }_{I}(q-1)^{n}[\widetilde{Z}_{I}]\hspace{-0.3pt}=\hspace{-0.3pt}q^{-(1/2)n(n-1)}\mathop{\prod }_{i=1}^{n-1}\frac{1}{q^{i}+\cdots +1}\mathop{\sum }_{I}[\widetilde{Z}_{I}].\nonumber\end{eqnarray}$$
The claim now follows from Lemma 4.2. ◻
Corollary 4.4. The multiple
![]() $(q-1)^{k}\int$
of the integral takes regular values on
$(q-1)^{k}\int$
of the integral takes regular values on
![]() $K^{{\leqslant}k}(\mathfrak{M})$
, for every
$K^{{\leqslant}k}(\mathfrak{M})$
, for every
![]() $k\geqslant 0$
.
$k\geqslant 0$
.

Proof. Consider the following diagram.

The dotted arrow exists because the square in the lower right of this diagram is cartesian, and the outer part of the diagram commutes. (Here we have identified the localization
![]() $K(\text{Var})_{(q-1)}$
with its image in
$K(\text{Var})_{(q-1)}$
with its image in
![]() $K(\text{St})(q)=K(\text{St})\otimes _{\mathbb{Q}[q]}\mathbb{Q}(q)$
.)◻
$K(\text{St})(q)=K(\text{St})\otimes _{\mathbb{Q}[q]}\mathbb{Q}(q)$
.)◻
Corollary 4.5. Defining
![]() $\int t=q-1$
extends the integral to a
$\int t=q-1$
extends the integral to a
![]() $K(\text{DM})$
-linear homomorphism
$K(\text{DM})$
-linear homomorphism
4.2 The integral versus the Hall product
The
 $\unicode[STIX]{x1D6E4}$
-indexed integral
$\unicode[STIX]{x1D6E4}$
-indexed integral
Let
![]() $\unicode[STIX]{x1D6E4}$
be a grading group for
$\unicode[STIX]{x1D6E4}$
be a grading group for
![]() $\mathfrak{M}$
, as in § 3.3. We assume, in addition, that
$\mathfrak{M}$
, as in § 3.3. We assume, in addition, that
![]() $\unicode[STIX]{x1D6E4}$
is endowed with a
$\unicode[STIX]{x1D6E4}$
is endowed with a
![]() $\mathbb{Z}$
-valued bilinear form
$\mathbb{Z}$
-valued bilinear form
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Definition 4.6. We say
![]() $\mathfrak{M}$
is hereditary if for every
$\mathfrak{M}$
is hereditary if for every
![]() $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}$
, the morphism
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}$
, the morphism
![]() $\mathfrak{E}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FE}}\times \mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
is a vector bundle stack [Reference Behrend and FantechiBF97, Definition 1.9] of rank
$\mathfrak{E}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FE}}\times \mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
is a vector bundle stack [Reference Behrend and FantechiBF97, Definition 1.9] of rank
![]() $-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
.
$-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})$
.
Let us assume henceforth that
![]() $\mathfrak{M}$
is hereditary.
$\mathfrak{M}$
is hereditary.
We define
![]() $K(\text{St})[\unicode[STIX]{x1D6E4}]$
to be the free
$K(\text{St})[\unicode[STIX]{x1D6E4}]$
to be the free
![]() $K(\text{St})$
-module on the symbols
$K(\text{St})$
-module on the symbols
![]() $u^{\unicode[STIX]{x1D6FE}}$
, for
$u^{\unicode[STIX]{x1D6FE}}$
, for
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, and introduce an associative product on
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}$
, and introduce an associative product on
![]() $K(\text{St})[\unicode[STIX]{x1D6E4}]$
by the formula
$K(\text{St})[\unicode[STIX]{x1D6E4}]$
by the formula
and extend it linearly to make
![]() $K(\text{St})[\unicode[STIX]{x1D6E4}]$
a
$K(\text{St})[\unicode[STIX]{x1D6E4}]$
a
![]() $K(\text{St})$
-algebra. Regular coefficients form a subalgebra
$K(\text{St})$
-algebra. Regular coefficients form a subalgebra
![]() $K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
.
$K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
.
We define the
![]() $\unicode[STIX]{x1D6E4}$
-indexed integral
$\unicode[STIX]{x1D6E4}$
-indexed integral
 $$\begin{eqnarray}\displaystyle \int :\mathscr{K}(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]\nonumber\\ \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FE}} & \longmapsto & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}u^{\unicode[STIX]{x1D6FE}}\int x_{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int :\mathscr{K}(\mathfrak{M}) & \longrightarrow & \displaystyle K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]\nonumber\\ \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}x_{\unicode[STIX]{x1D6FE}} & \longmapsto & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}}u^{\unicode[STIX]{x1D6FE}}\int x_{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
Proposition 4.7. If
![]() $\mathfrak{M}$
is hereditary, the
$\mathfrak{M}$
is hereditary, the
![]() $\unicode[STIX]{x1D6E4}$
-indexed integral preserves the star product. In fact, for
$\unicode[STIX]{x1D6E4}$
-indexed integral preserves the star product. In fact, for
![]() $x,y\in \mathscr{K}(\mathfrak{M})$
we have
$x,y\in \mathscr{K}(\mathfrak{M})$
we have
Proof. This is a straightforward calculation. One uses the fact that for
![]() $X\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
$X\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
and
![]() $Y\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
, the morphism
$Y\rightarrow \mathfrak{M}_{\unicode[STIX]{x1D6FD}}$
, the morphism
![]() $X\ast Y\rightarrow X\times Y$
is a vector bundle stack of rank
$X\ast Y\rightarrow X\times Y$
is a vector bundle stack of rank
![]() $-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})$
, and hence, in
$-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})$
, and hence, in
![]() $K(\text{St})$
, we have
$K(\text{St})$
, we have
![]() $[X\ast Y]=q^{-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})}[X][Y]$
.◻
$[X\ast Y]=q^{-\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD})}[X][Y]$
.◻
Semi-classical limit
We will pass to the semi-classical limit of the integral
![]() $\int :\mathscr{K}(\mathfrak{M})\rightarrow K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
by setting
$\int :\mathscr{K}(\mathfrak{M})\rightarrow K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
by setting
![]() $t=0$
(in the source) and hence
$t=0$
(in the source) and hence
![]() $q=1$
(in the target). As
$q=1$
(in the target). As
![]() $\int$
respects the
$\int$
respects the
![]() $\ast$
-product, the semi-classical limit will be a morphism of Poisson algebras.
$\ast$
-product, the semi-classical limit will be a morphism of Poisson algebras.
Modulo
![]() $(q-1)$
, the star product on
$(q-1)$
, the star product on
![]() $K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
is commutative; in fact, modulo
$K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]$
is commutative; in fact, modulo
![]() $(q-1)$
it is given by the commutative product
$(q-1)$
it is given by the commutative product
![]() $u^{\unicode[STIX]{x1D6FE}}\cdot u^{\unicode[STIX]{x1D6FD}}=u^{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}}$
. Hence, the quotient
$u^{\unicode[STIX]{x1D6FE}}\cdot u^{\unicode[STIX]{x1D6FD}}=u^{\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D6FD}}$
. Hence, the quotient
![]() $K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]/(q-1)$
inherits a Poisson bracket, defined by
$K(\text{St})_{\text{reg}}[\unicode[STIX]{x1D6E4}]/(q-1)$
inherits a Poisson bracket, defined by
Explicitly, it is given by
where
![]() $\widetilde{\unicode[STIX]{x1D712}}$
is (twice) the anti-symmetrization of
$\widetilde{\unicode[STIX]{x1D712}}$
is (twice) the anti-symmetrization of
![]() $\unicode[STIX]{x1D712}$
:
$\unicode[STIX]{x1D712}$
:
We conclude the following result.
Theorem 4.8. If
![]() $\mathfrak{M}$
is hereditary, we have a morphism of Poisson algebras
$\mathfrak{M}$
is hereditary, we have a morphism of Poisson algebras
The Poisson structure on
![]() $K(\mathfrak{M})$
is described in § 3.2; the one on
$K(\mathfrak{M})$
is described in § 3.2; the one on
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
, above, see (37). The
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
, above, see (37). The
![]() $u^{\unicode[STIX]{x1D6FE}}$
coefficient of the integral
$u^{\unicode[STIX]{x1D6FE}}$
coefficient of the integral
![]() $\int _{q=1}$
may be expressed as
$\int _{q=1}$
may be expressed as
for
![]() $x\in K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
. Here we have used the operator
$x\in K(\mathfrak{M})_{\unicode[STIX]{x1D6FE}}$
. Here we have used the operator
![]() $\unicode[STIX]{x1D70B}_{t}$
of Definition 2.11 and substituted
$\unicode[STIX]{x1D70B}_{t}$
of Definition 2.11 and substituted
![]() $t=q-1$
.
$t=q-1$
.
Proof. The homomorphism (38) is obtained by setting
![]() $t=0$
in (36). Note that the deformation parameter
$t=0$
in (36). Note that the deformation parameter
![]() $t$
is mapped to the deformation parameter
$t$
is mapped to the deformation parameter
![]() $(q-1)$
, so that the Poisson bracket (which depends on the choice of the deformation parameter) is preserved.
$(q-1)$
, so that the Poisson bracket (which depends on the choice of the deformation parameter) is preserved.
To calculate
![]() $\int _{q=1}$
, note that
$\int _{q=1}$
, note that
![]() $x\mapsto \unicode[STIX]{x1D70B}_{t}(x)$
is a section of the quotient map
$x\mapsto \unicode[STIX]{x1D70B}_{t}(x)$
is a section of the quotient map
![]() $\mathscr{K}(\mathfrak{M})\rightarrow K(\mathfrak{M})$
, obtained by setting
$\mathscr{K}(\mathfrak{M})\rightarrow K(\mathfrak{M})$
, obtained by setting
![]() $t=0$
. This gives rise to the displayed formula.◻
$t=0$
. This gives rise to the displayed formula.◻
Remark 4.9. Note that the diagram

commutes. The central column is a morphism of one-parameter families of non-commutative algebras. The left-hand column is the general fibre and a morphism of non-commutative
![]() $K(\text{DM})\otimes \mathbb{Q}[t,1/t]$
-algebras; the right-hand column is the semi-classical limit and hence a morphism of Poisson algebras.
$K(\text{DM})\otimes \mathbb{Q}[t,1/t]$
-algebras; the right-hand column is the semi-classical limit and hence a morphism of Poisson algebras.
Restricting the theorem to the virtually indecomposable elements, we obtain the following result.
Corollary 4.10. The semi-classical limit of the integral defines a morphism of Lie algebras over
![]() $K(\text{DM})$
:
$K(\text{DM})$
:
The bracket in
![]() $K^{\text{vir}}(\mathfrak{M})$
is the commutator bracket of the Hall product, and the bracket in
$K^{\text{vir}}(\mathfrak{M})$
is the commutator bracket of the Hall product, and the bracket in
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
is given in (37). The integral
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}]$
is given in (37). The integral
![]() $\int _{q=1}$
is given by the formula
$\int _{q=1}$
is given by the formula
for a virtually indecomposable Hall algebra element
![]() $x\in K^{\text{vir}}(\mathfrak{M})$
.
$x\in K^{\text{vir}}(\mathfrak{M})$
.
Remark 4.11. We have a surjective morphism of
![]() $K(\text{Var})$
-algebras
$K(\text{Var})$
-algebras
and an isomorphism
The former morphism is (most likely) not injective, because there is no (obvious) reason why elements in
![]() $\operatorname{Ann}(q-1)\subset K(\text{Var})$
should map to zero in
$\operatorname{Ann}(q-1)\subset K(\text{Var})$
should map to zero in
![]() $K(\text{Var})/(q-1)$
, although they certainly map to zero in
$K(\text{Var})/(q-1)$
, although they certainly map to zero in
![]() $K(\text{St})_{\text{reg}}/(q-1)$
.
$K(\text{St})_{\text{reg}}/(q-1)$
.
Without too much more effort, it is possible to prove that the semi-classical limit of the integral lifts to a
![]() $K(\text{Var})$
-linear homomorphism
$K(\text{Var})$
-linear homomorphism
Unfortunately, we cannot, at the moment, prove that this lift is a morphism of Poisson algebras.
Remark 4.12. Let
![]() $\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
be a submonoid as above, i.e., having the property that every
$\unicode[STIX]{x1D6E4}_{+}\subset \unicode[STIX]{x1D6E4}$
be a submonoid as above, i.e., having the property that every
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
admits only finitely many decompositions
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
admits only finitely many decompositions
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
, with both
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
, with both
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
, and such that the intersection of all cofinite ideals is empty.
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6E4}_{+}$
, and such that the intersection of all cofinite ideals is empty.
For every ideal
![]() $S\subset \unicode[STIX]{x1D6E4}_{+}$
, the group
$S\subset \unicode[STIX]{x1D6E4}_{+}$
, the group
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{S}]$
is an ideal in
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{S}]$
is an ideal in
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]$
, and we let
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]$
, and we let
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]^{\wedge }$
be the completion of
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]^{\wedge }$
be the completion of
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]$
with respect to this collection of ideals.
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]$
with respect to this collection of ideals.
The restriction of the semi-classical integral
is continuous with respect to the filtrations induced by the cofinite ideals in
![]() $\unicode[STIX]{x1D6E4}_{+}$
and hence extends to the completions, giving rise to a morphism of Poisson-algebras
$\unicode[STIX]{x1D6E4}_{+}$
and hence extends to the completions, giving rise to a morphism of Poisson-algebras
and a morphism of Lie algebras
If we now have a substack
![]() $\mathfrak{N}\,\subset \,\mathfrak{M}$
as above, i.e., every
$\mathfrak{N}\,\subset \,\mathfrak{M}$
as above, i.e., every
![]() $\mathfrak{N}_{\unicode[STIX]{x1D6FE}}=\mathfrak{N}\,\cap \,\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
is of finite type,
$\mathfrak{N}_{\unicode[STIX]{x1D6FE}}=\mathfrak{N}\,\cap \,\mathfrak{M}_{\unicode[STIX]{x1D6FE}}$
is of finite type,
![]() $\mathfrak{N}$
is closed under direct sums and extensions in
$\mathfrak{N}$
is closed under direct sums and extensions in
![]() $\mathfrak{M}$
, and
$\mathfrak{M}$
, and
![]() $\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\not =\varnothing$
only if
$\mathfrak{N}_{\unicode[STIX]{x1D6FE}}\not =\varnothing$
only if
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
, we can form
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{+}$
, we can form
![]() $\unicode[STIX]{x1D700}_{1}[\mathfrak{N}]\in \hat{K}^{\text{vir}}(\mathfrak{M})_{+}$
and apply to it the semi-classical integral
$\unicode[STIX]{x1D700}_{1}[\mathfrak{N}]\in \hat{K}^{\text{vir}}(\mathfrak{M})_{+}$
and apply to it the semi-classical integral
![]() $\int _{q=1}$
to obtain the Joyce-type invariant
$\int _{q=1}$
to obtain the Joyce-type invariant
 $$\begin{eqnarray}\displaystyle \int _{q=1}\unicode[STIX]{x1D700}_{1}[\mathfrak{N}] & = & \displaystyle \int _{q=1}\log _{\ast }(1+[\mathfrak{N}])\nonumber\\ \displaystyle & = & \displaystyle \biggl((q-1)\mathop{\sum }_{\substack{ n\geqslant 1 \\ \unicode[STIX]{x1D6FE}_{1}\,\ldots ,\unicode[STIX]{x1D6FE}_{n}\in \unicode[STIX]{x1D6E4}_{+}}}\frac{(-1)^{n+1}}{n}[\mathfrak{N}_{\unicode[STIX]{x1D6FE}_{1}}]\ast \cdots \ast [\mathfrak{N}_{\unicode[STIX]{x1D6FE}_{n}}]\biggr)\bigg|_{q=1}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{q=1}\unicode[STIX]{x1D700}_{1}[\mathfrak{N}] & = & \displaystyle \int _{q=1}\log _{\ast }(1+[\mathfrak{N}])\nonumber\\ \displaystyle & = & \displaystyle \biggl((q-1)\mathop{\sum }_{\substack{ n\geqslant 1 \\ \unicode[STIX]{x1D6FE}_{1}\,\ldots ,\unicode[STIX]{x1D6FE}_{n}\in \unicode[STIX]{x1D6E4}_{+}}}\frac{(-1)^{n+1}}{n}[\mathfrak{N}_{\unicode[STIX]{x1D6FE}_{1}}]\ast \cdots \ast [\mathfrak{N}_{\unicode[STIX]{x1D6FE}_{n}}]\biggr)\bigg|_{q=1}\end{eqnarray}$$
in
![]() $K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]^{\wedge }$
.
$K(\text{St})_{\text{reg}}/(q-1)[\unicode[STIX]{x1D6E4}_{+}]^{\wedge }$
.
Acknowledgements
The idea to consider the inertia stack as an operator on
![]() $K$
-groups of stacks and motivic Hall algebras, and to study its eigenspace decomposition to understand Joyce’s work in a more conceptual fashion, is due to Tom Bridgeland. In particular, the conjecture that the semi-simple inertia operator is diagonalizable is due to him. We would like to thank Tom Bridgeland for sharing his ideas with us. We would also like to thank Dominic Joyce and Arend Bayer for fruitful discussions. Finally, we would like to thank two anonymous referees for helpful comments and suggestions.
$K$
-groups of stacks and motivic Hall algebras, and to study its eigenspace decomposition to understand Joyce’s work in a more conceptual fashion, is due to Tom Bridgeland. In particular, the conjecture that the semi-simple inertia operator is diagonalizable is due to him. We would like to thank Tom Bridgeland for sharing his ideas with us. We would also like to thank Dominic Joyce and Arend Bayer for fruitful discussions. Finally, we would like to thank two anonymous referees for helpful comments and suggestions.
Appendix Comparison with Joyce’s virtual projections in an example
Let us write
![]() $[n]=[B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
. We have (cf. Remark 3.21)
$[n]=[B\operatorname{GL}_{n}\rightarrow \mathfrak{Vect}]\in K(\mathfrak{Vect})$
. We have (cf. Remark 3.21)
This gives us
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{k}[n] & = & \displaystyle \mathop{\sum }_{r}\frac{s(r,k)}{r!}E_{r}[n]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r}\frac{s(r,k)}{r!}\mathop{\sum }_{\substack{ \ell _{1}+\cdots +\ell _{r}=n \\ \ell _{1}\ldots \ell _{r}>0}}[\ell _{1}]\cdots [\ell _{r}]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\vdash n}\frac{s(\ell (\unicode[STIX]{x1D706}),k)}{|\!\operatorname{Aut}\unicode[STIX]{x1D706}|}\mathop{\prod }_{i}[\unicode[STIX]{x1D706}_{i}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{k}[n] & = & \displaystyle \mathop{\sum }_{r}\frac{s(r,k)}{r!}E_{r}[n]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r}\frac{s(r,k)}{r!}\mathop{\sum }_{\substack{ \ell _{1}+\cdots +\ell _{r}=n \\ \ell _{1}\ldots \ell _{r}>0}}[\ell _{1}]\cdots [\ell _{r}]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}\vdash n}\frac{s(\ell (\unicode[STIX]{x1D706}),k)}{|\!\operatorname{Aut}\unicode[STIX]{x1D706}|}\mathop{\prod }_{i}[\unicode[STIX]{x1D706}_{i}].\nonumber\end{eqnarray}$$
We remark also that the formula of Remark 2.12 gives us
which contains the above formulas for
![]() $\unicode[STIX]{x1D70B}_{k}[n]$
.
$\unicode[STIX]{x1D70B}_{k}[n]$
.
In [Reference JoyceJoy07b, §5.2], Joyce defines projection operators
![]() $\unicode[STIX]{x1D6F1}_{n}^{\text{vi}}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
, which pairwise commute and add up to the identity (although he works with bare algebraic stacks, not algebroids). We expect that modulo this difference, we have
$\unicode[STIX]{x1D6F1}_{n}^{\text{vi}}:K(\mathfrak{M})\rightarrow K(\mathfrak{M})$
, which pairwise commute and add up to the identity (although he works with bare algebraic stacks, not algebroids). We expect that modulo this difference, we have
We will prove that these operators take the same values on the elements
![]() $[n]\in K(\mathfrak{Vect})$
.
$[n]\in K(\mathfrak{Vect})$
.
Proposition A.1. We have
for all
![]() $k$
and
$k$
and
![]() $n$
.
$n$
.
Proof. Let
![]() $T_{n}$
be the
$T_{n}$
be the
![]() $n$
-dimensional torus of diagonal matrices inside
$n$
-dimensional torus of diagonal matrices inside
![]() $\operatorname{GL}_{n}$
.
$\operatorname{GL}_{n}$
.
Joyce’s
![]() ${\mathcal{P}}$
set [Reference JoyceJoy07b, Definition 5.3] is trivial in this case because as a quotient stack
${\mathcal{P}}$
set [Reference JoyceJoy07b, Definition 5.3] is trivial in this case because as a quotient stack
![]() $B\operatorname{GL}_{n}=\ast /\!\operatorname{GL}_{n}$
where
$B\operatorname{GL}_{n}=\ast /\!\operatorname{GL}_{n}$
where
![]() $\ast$
is a point, so
$\ast$
is a point, so
![]() ${\mathcal{P}}(\ast ,T_{n})=\{T_{n}\}$
. The
${\mathcal{P}}(\ast ,T_{n})=\{T_{n}\}$
. The
![]() ${\mathcal{Q}}$
set
${\mathcal{Q}}$
set
![]() ${\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
is computed in [Reference JoyceJoy07b, Example 5.7] to be the set of all tori
${\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
is computed in [Reference JoyceJoy07b, Example 5.7] to be the set of all tori
where
![]() $\unicode[STIX]{x1D711}$
ranges over all surjection maps
$\unicode[STIX]{x1D711}$
ranges over all surjection maps
![]() $\unicode[STIX]{x1D711}:\text{}\underline{n}\rightarrow \text{}\underline{r}$
. Finally, the
$\unicode[STIX]{x1D711}:\text{}\underline{n}\rightarrow \text{}\underline{r}$
. Finally, the
![]() ${\mathcal{R}}$
set coincides with
${\mathcal{R}}$
set coincides with
![]() ${\mathcal{Q}}$
. Joyce’s definition then needs computation of
${\mathcal{Q}}$
. Joyce’s definition then needs computation of
![]() $M_{G}^{X}(P,Q,R)$
, where
$M_{G}^{X}(P,Q,R)$
, where
![]() $P$
,
$P$
,
![]() $Q$
, and
$Q$
, and
![]() $R$
are selected respectively from
$R$
are selected respectively from
![]() ${\mathcal{P}}$
,
${\mathcal{P}}$
,
![]() ${\mathcal{Q}}$
, and
${\mathcal{Q}}$
, and
![]() ${\mathcal{R}}$
. In our case, this is
${\mathcal{R}}$
. In our case, this is
for all choices of
![]() $R,Q\in {\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
such that
$R,Q\in {\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
such that
![]() $R\subseteq Q$
. Now we unwind the definition of
$R\subseteq Q$
. Now we unwind the definition of
![]() $n_{T_{n}}^{\operatorname{GL}_{n}}(R,Q)$
.
$n_{T_{n}}^{\operatorname{GL}_{n}}(R,Q)$
.
 $$\begin{eqnarray}\displaystyle n(R,Q)=\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=R}}(-1)^{|B|-1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n(R,Q)=\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=R}}(-1)^{|B|-1}. & & \displaystyle \nonumber\end{eqnarray}$$
We can finally define the virtual projections of
![]() $B\operatorname{GL}_{n}$
as
$B\operatorname{GL}_{n}$
as
We say
![]() $Q\in {\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
is of ‘type
$Q\in {\mathcal{Q}}(\operatorname{GL}_{n},T_{n})$
is of ‘type
![]() $\unicode[STIX]{x1D70E}$
’ if the corresponding surjection
$\unicode[STIX]{x1D70E}$
’ if the corresponding surjection
![]() $\unicode[STIX]{x1D711}:\{1,\ldots ,n\}\rightarrow \{1,\ldots ,r\}$
induces the partition
$\unicode[STIX]{x1D711}:\{1,\ldots ,n\}\rightarrow \{1,\ldots ,r\}$
induces the partition
![]() $\unicode[STIX]{x1D70E}\vdash n$
. Note that there are
$\unicode[STIX]{x1D70E}\vdash n$
. Note that there are
![]() $n!/\unicode[STIX]{x1D70E}_{1}!\cdots \unicode[STIX]{x1D70E}_{n}!(1!)^{\unicode[STIX]{x1D70E}_{1}}\cdots (n!)^{\unicode[STIX]{x1D70E}_{n}}$
of them. Also,
$n!/\unicode[STIX]{x1D70E}_{1}!\cdots \unicode[STIX]{x1D70E}_{n}!(1!)^{\unicode[STIX]{x1D70E}_{1}}\cdots (n!)^{\unicode[STIX]{x1D70E}_{n}}$
of them. Also,
![]() $C_{\operatorname{GL}_{n}}Q$
depends only on the type of
$C_{\operatorname{GL}_{n}}Q$
depends only on the type of
![]() $Q$
and is isomorphic to
$Q$
and is isomorphic to
![]() $\prod _{i=1}^{n}[\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}}$
. The normalizer of
$\prod _{i=1}^{n}[\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}}$
. The normalizer of
![]() $T_{n}$
is
$T_{n}$
is
![]() $S_{n}\ltimes T^{n}$
, and therefore
$S_{n}\ltimes T^{n}$
, and therefore
and
We have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{k}^{vi}(B\operatorname{GL}_{n}) & = & \displaystyle \mathop{\sum }_{R:\dim R=k}\mathop{\sum }_{Q:R\subseteq Q}M_{\operatorname{GL}_{n}}^{\ast }(T_{n},Q,R)[BC_{G}(Q)]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q}\biggl|\frac{N_{\operatorname{GL}_{n}}(T_{n})}{C_{\operatorname{GL}_{n}}(Q)\cap N_{\operatorname{GL}_{n}}(T_{n})}\biggr|^{-1}\!\biggl(\mathop{\sum }_{\substack{ R\subseteq Q \\ \dim R=k}}n_{T_{n}}^{\operatorname{GL}_{n}}(R,Q)\biggr)[BC_{G}(Q)]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}(\#Q\text{ of type }\unicode[STIX]{x1D70E}).\frac{(1!)^{\unicode[STIX]{x1D70E}_{1}}\cdots (n!)^{\unicode[STIX]{x1D70E}_{n}}}{n!}s(\ell (\unicode[STIX]{x1D70E}),k)\mathop{\prod }_{i=1}^{n}[B\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}\frac{1}{\unicode[STIX]{x1D70E}_{1}!\cdots \unicode[STIX]{x1D70E}_{n}!}s(\ell (\unicode[STIX]{x1D70E}),k)\mathop{\prod }_{i=1}^{n}[B\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{k}^{vi}(B\operatorname{GL}_{n}) & = & \displaystyle \mathop{\sum }_{R:\dim R=k}\mathop{\sum }_{Q:R\subseteq Q}M_{\operatorname{GL}_{n}}^{\ast }(T_{n},Q,R)[BC_{G}(Q)]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{Q}\biggl|\frac{N_{\operatorname{GL}_{n}}(T_{n})}{C_{\operatorname{GL}_{n}}(Q)\cap N_{\operatorname{GL}_{n}}(T_{n})}\biggr|^{-1}\!\biggl(\mathop{\sum }_{\substack{ R\subseteq Q \\ \dim R=k}}n_{T_{n}}^{\operatorname{GL}_{n}}(R,Q)\biggr)[BC_{G}(Q)]\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}(\#Q\text{ of type }\unicode[STIX]{x1D70E}).\frac{(1!)^{\unicode[STIX]{x1D70E}_{1}}\cdots (n!)^{\unicode[STIX]{x1D70E}_{n}}}{n!}s(\ell (\unicode[STIX]{x1D70E}),k)\mathop{\prod }_{i=1}^{n}[B\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}\frac{1}{\unicode[STIX]{x1D70E}_{1}!\cdots \unicode[STIX]{x1D70E}_{n}!}s(\ell (\unicode[STIX]{x1D70E}),k)\mathop{\prod }_{i=1}^{n}[B\operatorname{GL}_{i}]^{\unicode[STIX]{x1D70E}_{i}},\nonumber\end{eqnarray}$$
where the third line follows from the lemma below. We conclude that Joyce’s virtual projections of
![]() $B\operatorname{GL}_{n}$
are identical to our eigenprojections.◻
$B\operatorname{GL}_{n}$
are identical to our eigenprojections.◻
Lemma A.2. For a
![]() $Q$
of type
$Q$
of type
![]() $\unicode[STIX]{x1D70E}$
, we have
$\unicode[STIX]{x1D70E}$
, we have
Proof. We let
![]() $m=\dim Q=\ell (\unicode[STIX]{x1D70E})$
in this proof. Obviously, if
$m=\dim Q=\ell (\unicode[STIX]{x1D70E})$
in this proof. Obviously, if
![]() $\ell (\unicode[STIX]{x1D70E})<k$
, there is no possible choice of
$\ell (\unicode[STIX]{x1D70E})<k$
, there is no possible choice of
therefore proving
In the case that
![]() $\ell (\unicode[STIX]{x1D70E})=k$
, the only choice of
$\ell (\unicode[STIX]{x1D70E})=k$
, the only choice of
![]() $R$
is
$R$
is
![]() $Q$
itself and the only choice of
$Q$
itself and the only choice of
![]() $B$
is the set
$B$
is the set
![]() $B=\{Q\}$
. This proves
$B=\{Q\}$
. This proves
All other values of
![]() $s(\ell (\unicode[STIX]{x1D70E}),k)$
are defined recursively by
$s(\ell (\unicode[STIX]{x1D70E}),k)$
are defined recursively by
So it suffices to show that
![]() $\sum _{R:\dim R=k}n(R,Q)$
satisfies the same recursive relation.
$\sum _{R:\dim R=k}n(R,Q)$
satisfies the same recursive relation.
For any choice of
![]() $R$
,
$R$
,
 $$\begin{eqnarray}n(R,Q)=\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=R}}(-1)^{|B|-1}\end{eqnarray}$$
$$\begin{eqnarray}n(R,Q)=\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=R}}(-1)^{|B|-1}\end{eqnarray}$$
can also be computed by choosing only those
![]() $\hat{Q}$
that are codimension 1 inside
$\hat{Q}$
that are codimension 1 inside
![]() $Q$
. This is because for every
$Q$
. This is because for every
![]() $\hat{Q}$
of codimension
$\hat{Q}$
of codimension
![]() ${>}2$
, the number
${>}2$
, the number
![]() $t$
of intermediate subtori
$t$
of intermediate subtori
![]() $Q^{\prime }$
$Q^{\prime }$
is positive, and therefore
![]() $B$
containing
$B$
containing
![]() $\hat{Q}$
is included in
$\hat{Q}$
is included in
![]() $2^{t}$
possible choices of
$2^{t}$
possible choices of
![]() $B$
with cancelling size parities.
$B$
with cancelling size parities.
Let us write the points of
![]() $Q$
as
$Q$
as
![]() $m$
-tuples
$m$
-tuples
![]() $(x_{1},\ldots ,x_{m})$
with
$(x_{1},\ldots ,x_{m})$
with
![]() $x_{i}\in \mathbb{G}_{m}$
. Let
$x_{i}\in \mathbb{G}_{m}$
. Let
![]() $W$
be the
$W$
be the
![]() $(m-1)$
-dimensional torus consisting of points
$(m-1)$
-dimensional torus consisting of points
![]() $(x_{1},\ldots ,x_{m-1})$
. Any
$(x_{1},\ldots ,x_{m-1})$
. Any
![]() $R$
with
$R$
with
![]() $\dim R=k$
is given by a set of defining equations
$\dim R=k$
is given by a set of defining equations
In the defining equation of
![]() $R$
with
$R$
with
![]() $\dim R=k$
, either
$\dim R=k$
, either
![]() $x_{m}$
does not appear, in which case
$x_{m}$
does not appear, in which case
![]() $R|_{W}$
is
$R|_{W}$
is
![]() $(k-1)$
-dimensional, or
$(k-1)$
-dimensional, or
![]() $x_{m}$
does appear, in which case
$x_{m}$
does appear, in which case
![]() $R|_{W}$
is
$R|_{W}$
is
![]() $k$
-dimensional and any choice of
$k$
-dimensional and any choice of
![]() $B$
consisting of only codimension 1 elements satisfying
$B$
consisting of only codimension 1 elements satisfying
![]() $\bigcap _{\hat{Q}\in B}\hat{Q}=R$
loses one of its elements after restriction to
$\bigcap _{\hat{Q}\in B}\hat{Q}=R$
loses one of its elements after restriction to
![]() $R|_{W}$
. This shows that
$R|_{W}$
. This shows that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k}}(-1)^{|B|-1} & = & \displaystyle \mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq W\} \\ W\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k-1}}(-1)^{|B|-1}\nonumber\\ \displaystyle & & \displaystyle -\,(m-1)\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq W\} \\ W\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k}}(-1)^{|B|-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq Q\} \\ Q\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k}}(-1)^{|B|-1} & = & \displaystyle \mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq W\} \\ W\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k-1}}(-1)^{|B|-1}\nonumber\\ \displaystyle & & \displaystyle -\,(m-1)\mathop{\sum }_{\substack{ B\subseteq \{\hat{Q}\in {\mathcal{Q}}:\hat{Q}\subseteq W\} \\ W\in B,\dim \mathop{\bigcap }_{\hat{Q}\in B}\hat{Q}=k}}(-1)^{|B|-1}\nonumber\end{eqnarray}$$
which completes the proof. ◻






