Article contents
Bounding the covolume of lattices in products
Published online by Cambridge University Press: 11 October 2019
Abstract
We study lattices in a product 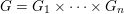 $G=G_{1}\times \cdots \times G_{n}$ of non-discrete, compactly generated, totally disconnected locally compact (tdlc) groups. We assume that each factor is quasi just-non-compact, meaning that
$G=G_{1}\times \cdots \times G_{n}$ of non-discrete, compactly generated, totally disconnected locally compact (tdlc) groups. We assume that each factor is quasi just-non-compact, meaning that 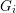 $G_{i}$ is non-compact and every closed normal subgroup of
$G_{i}$ is non-compact and every closed normal subgroup of 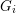 $G_{i}$ is discrete or cocompact (e.g.
$G_{i}$ is discrete or cocompact (e.g. 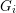 $G_{i}$ is topologically simple). We show that the set of discrete subgroups of
$G_{i}$ is topologically simple). We show that the set of discrete subgroups of 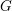 $G$ containing a fixed cocompact lattice
$G$ containing a fixed cocompact lattice 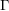 $\unicode[STIX]{x1D6E4}$ with dense projections is finite. The same result holds if
$\unicode[STIX]{x1D6E4}$ with dense projections is finite. The same result holds if 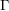 $\unicode[STIX]{x1D6E4}$ is non-uniform, provided
$\unicode[STIX]{x1D6E4}$ is non-uniform, provided 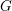 $G$ has Kazhdan’s property (T). We show that for any compact subset
$G$ has Kazhdan’s property (T). We show that for any compact subset 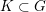 $K\subset G$, the collection of discrete subgroups
$K\subset G$, the collection of discrete subgroups 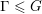 $\unicode[STIX]{x1D6E4}\leqslant G$ with
$\unicode[STIX]{x1D6E4}\leqslant G$ with 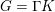 $G=\unicode[STIX]{x1D6E4}K$ and dense projections is uniformly discrete and hence of covolume bounded away from
$G=\unicode[STIX]{x1D6E4}K$ and dense projections is uniformly discrete and hence of covolume bounded away from 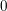 $0$. When the ambient group
$0$. When the ambient group 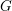 $G$ is compactly presented, we show in addition that the collection of those lattices falls into finitely many
$G$ is compactly presented, we show in addition that the collection of those lattices falls into finitely many 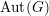 $\operatorname{Aut}(G)$-orbits. As an application, we establish finiteness results for discrete groups acting on products of locally finite graphs with semiprimitive local action on each factor. We also present several intermediate results of independent interest. Notably it is shown that if a non-discrete, compactly generated quasi just-non-compact tdlc group
$\operatorname{Aut}(G)$-orbits. As an application, we establish finiteness results for discrete groups acting on products of locally finite graphs with semiprimitive local action on each factor. We also present several intermediate results of independent interest. Notably it is shown that if a non-discrete, compactly generated quasi just-non-compact tdlc group 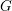 $G$ is a Chabauty limit of discrete subgroups, then some compact open subgroup of
$G$ is a Chabauty limit of discrete subgroups, then some compact open subgroup of 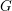 $G$ is an infinitely generated pro-
$G$ is an infinitely generated pro-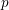 $p$ group for some prime
$p$ group for some prime 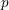 $p$. It is also shown that in any Kazhdan group with discrete amenable radical, the lattices form an open subset of the Chabauty space of closed subgroups.
$p$. It is also shown that in any Kazhdan group with discrete amenable radical, the lattices form an open subset of the Chabauty space of closed subgroups.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
The first author is an F.R.S.-FNRS Senior Research Associate. The second author is a CNRS Researcher. This work was partially carried out when the second author was an F.R.S.-FNRS Post-Doctoral Researcher at UCLouvain. This work was partially supported by ANR-14-CE25-0004 GAMME.
References
- 4
- Cited by




