Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-27T03:38:41.231Z Has data issue: false hasContentIssue false
  • English
  • Français

An inhomogeneous Dirichlet theorem via shrinking targets

Part of: Ergodic theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  25 June 2019

Dmitry Kleinbock  and
Nick Wadleigh
Dmitry Kleinbock
Affiliation:
Brandeis University, Waltham, MA 02454-9110, USA email kleinboc@brandeis.edu
Nick Wadleigh
Affiliation:
Brandeis University, Waltham, MA 02454-9110, USA email wadleigh@brandeis.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an integrability criterion on a real-valued non-increasing function $\unicode[STIX]{x1D713}$ guaranteeing that for almost all (or almost no) pairs 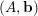$(A,\mathbf{b})$, where 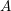$A$ is a real 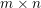$m\times n$ matrix and 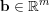$\mathbf{b}\in \mathbb{R}^{m}$, the system

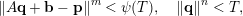$$\begin{eqnarray}\Vert A\mathbf{q}+\mathbf{b}-\mathbf{p}\Vert ^{m}<\unicode[STIX]{x1D713}(T),\quad \Vert \mathbf{q}\Vert ^{n}<T,\end{eqnarray}$$
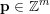is solvable in $\mathbf{p}\in \mathbb{Z}^{m}$, 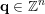$\mathbf{q}\in \mathbb{Z}^{n}$ for all sufficiently large 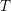$T$. The proof consists of a reduction to a shrinking target problem on the space of grids in 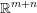$\mathbb{R}^{m+n}$. We also comment on the homogeneous counterpart to this problem, whose 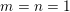$m=n=1$ case was recently solved, but whose general case remains open.

Keywords

Dirichlet’s theoreminhomogeneous Diophantine approximationspace of gridsshrinking targetsexponential mixing

MSC classification

Primary: 11J20: Inhomogeneous linear forms
Secondary: 11J13: Simultaneous homogeneous approximation, linear forms 37A17: Homogeneous flows
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 7 , July 2019 , pp. 1402 - 1423
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first-named author was supported by NSF grants DMS-1101320 and DMS-1600814.

References

Athreya, J., Random affine lattices , Contemp. Math. 639 (2015), 169–174.10.1090/conm/639/12793Google Scholar
Bekka, M. B. and Mayer, M., Ergodic theory and topological dynamics of group actions on homogeneous spaces, London Mathematical Society Lecture Note Series, vol. 269 (Cambridge University Press, Cambridge, 2000).10.1017/CBO9780511758898Google Scholar
Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for lim sup sets , Mem. Amer. Math. Soc. 179 (2006).Google Scholar
Brezin, J. and Moore, C. C., Flows on homogeneous spaces: a new look , Amer. J. Math. 103 (1981), 571–613.10.2307/2374105Google Scholar
Cassels, J. W. S., An introduction to Diophantine approximation, Cambridge Tracts, vol. 45 (Cambridge University Press, Cambridge, 1957).Google Scholar
Cassels, J. W. S., An introduction to the geometry of numbers, Grundlehren der mathematischen Wissenschaften, Band 99 (Springer, Berlin, 1971).Google Scholar
Dani, S. G., Divergent trajectories of flows on homogeneous spaces and Diophantine approximation , J. Reine Angew. Math. 359 (1985), 55–89.Google Scholar
Davenport, H. and Schmidt, W. M., Dirichlet’s theorem on diophantine approximation. II , Acta Arith. 16 (1969/1970), 413–424.10.4064/aa-16-4-413-424Google Scholar
Davenport, H. and Schmidt, W. M., Dirichlet’s theorem on diophantine approximation, Symposia Mathematica, vol. IV (Academic, 1970).Google Scholar
Edwards, S., The rate of mixing for diagonal flows on spaces of affine lattices, Preprint (2013), http://uu.diva-portal.org/smash/get/diva2:618047/FULLTEXT01.pdf.Google Scholar
Einsiedler, M. and Tseng, J., Badly approximable systems of affine forms, fractals, and Schmidt games , J. Reine Angew. Math. 660 (2011), 83–97.Google Scholar
Ghosh, A., Gorodnik, A. and Nevo, A., Best possible rates of distribution of dense lattice orbits in homogeneous spaces , J. Reine Angew. Math. 745 (2018), 155–188.10.1515/crelle-2016-0001Google Scholar
Gorodnik, A. and Vishe, P., Simultaneous Diophantine approximation – logarithmic improvements , Trans. Amer. Math. Soc. 370 (2018), 487–507.10.1090/tran/6953Google Scholar
Groshev, A. V., Une théorème sur les systèmes des formes linéaires , Dokl. Akad. Nauk SSSR 9 (1938), 151–152.Google Scholar
Howe, R. and Tan, E.-C., Nonabelian harmonic analysis. Applications of [[()[]mml:mo lspace="1em" rspace="0em"[]()]]SL[[()[]/mml:mo[]()]](2, ℝ), Universitext (Springer, New York, 1992).Google Scholar
Hussain, M., Kleinbock, D., Wadleigh, N. and Wang, B.-W., Hausdorff measure of sets of Dirichlet non-improvable numbers , Mathematika 64 (2018), 502–518.10.1112/S0025579318000074Google Scholar
Katok, A. and Spatzier, R., First cohomology of Anosov actions of higher rank Abelian groups and applications to rigidity , Publ. Math. Inst. Hautes Études Sci. 79 (1994), 131–156.10.1007/BF02698888Google Scholar
Kelmer, D., Shrinking targets for discrete time flows on hyperbolic manifolds , Geom. Funct. Anal. 27 (2017), 1257–1287.10.1007/s00039-017-0421-zGoogle Scholar
Kim, D. H. and Liao, L., Dirichlet uniformly well-approximated numbers , Int. Math. Res. Not. IMRN, rny015, doi:10.1093/imrn/rny015.Google Scholar
Kleinbock, D., Badly approximable systems of affine forms , J. Number Theory 79 (1999), 83–102.10.1006/jnth.1999.2419Google Scholar
Kleinbock, D. and Margulis, G. A., Logarithm laws for flows on homogeneous spaces , Invent. Math. 138 (1999), 451–494.10.1007/s002220050350Google Scholar
Kleinbock, D. and Margulis, G. A., Erratum to: Logarithm laws for flows on homogeneous spaces , Invent. Math. 211 (2018), 855–862.10.1007/s00222-017-0751-3Google Scholar
Kleinbock, D. and Wadleigh, N., A zero-one law for improvements to Dirichlet’s theorem , Proc. Amer. Math. Soc. 146 (2018), 1833–1844.10.1090/proc/13685Google Scholar
Kleinbock, D. and Weiss, B., Dirichlet’s theorem on diophantine approximation and homogeneous flows , J. Mod. Dyn. 4 (2008), 43–62.Google Scholar
Kelmer, D. and Yu, S., Shrinking target problems for flows on homogeneous spaces, Trans. Amer. Math. Soc., doi:10.1090/tran/7783.Google Scholar
Kleinbock, D. and Zhao, X., An application of lattice points counting to shrinking target problems , Discrete Contin. Dyn. Syst. 38 (2018), 155–168.10.3934/dcds.2018007Google Scholar
Margulis, G. A., Dynamical and ergodic properties of subgroup actions on homogeneous spaces with applications to number theory , in Proceedings of the International Congress of Mathematicians, Vol. I, II (Kyoto, 1990) (Mathematical Society of Japan, Tokyo, 1991), 193–215.Google Scholar
Maucourant, F., Dynamical Borel–Cantelli lemma for hyperbolic spaces , Israel J. Math. 152 (2006), 143–155.10.1007/BF02771980Google Scholar
Moore, C. C., Ergodicity of flows on homogeneous spaces , Amer. J. Math. 88 (1966), 154–178.10.2307/2373052Google Scholar
Morris, D. W., Introduction to arithmetic groups (Deductive Press, 2015).Google Scholar
Shah, N., Expanding translates of curves and Dirichlet–Minkowski theorem on linear forms , J. Amer. Math. Soc. 23 (2010), 563–589.10.1090/S0894-0347-09-00657-2Google Scholar
Shapira, U., A solution to a problem of Cassels and Diophantine properties of cubic numbers , Ann. of Math. (2) 173 (2011), 543–557.10.4007/annals.2011.173.1.11Google Scholar
Sprindžuk, V., Metric theory of Diophantine approximations (V. H. Winston and Sons, Washington DC, 1979), 45–48.Google Scholar
Waldschmidt, M., Recent advances in Diophantine approximation , in Number theory, analysis and geometry (Springer, New York, 2012), 659–704.Google Scholar