Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-28jzs Total loading time: 0.322 Render date: 2021-02-28T20:01:55.251Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Compositio Mathematica Compositio Mathematica

Article contents

Integral points of bounded degree on affine curves

Part of: Arithmetic algebraic geometry Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  26 November 2015

Aaron Levin
Aaron Levin
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA email adlevin@math.msu.edu
Corresponding
E-mail address:
adlevin@math.msu.edu
Get access
Rights & Permissions[Opens in a new window]

Abstract

We generalize Siegel’s theorem on integral points on affine curves to integral points of bounded degree, giving a complete characterization of affine curves with infinitely many integral points of degree 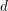$d$ or less over some number field. Generalizing Picard’s theorem, we prove an analogous result characterizing complex affine curves admitting a nonconstant holomorphic map from a degree 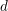$d$ (or less) analytic cover of 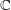$\mathbb{C}$ .

Keywords

integral points bounded degree Siegel’s theorem Picard’s theorem

MSC classification

Primary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields
Secondary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 4 , April 2016 , pp. 754 - 768
Copyright
© The Author 2015 

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

Abramovich, D. and Harris, J., Abelian varieties and curves in W d(C), Compositio Math. 78 (1991), 227–238.Google Scholar
Alvanos, P., Bilu, Y. and Poulakis, D., Characterizing algebraic curves with infinitely many integral points, Int. J. Number Theory 5 (2009), 585–590.CrossRefGoogle Scholar
Bloch, A., Sur les systèmes de fonctions uniformes satisfaisant à l’équation d’une variété algébrique dont l’irrégularité dépasse la dimension, J. Math. Pures Appl. 5 (1926), 9–66.Google Scholar
Bombieri, E., On Weil’s ‘théorème de décomposition’, Amer. J. Math. 105 (1983), 295–308.CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry, New Mathematical Monographs, vol. 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Corvaja, P. and Zannier, U., On integral points on surfaces, Ann. of Math. (2) 160 (2004), 705–726.CrossRefGoogle Scholar
Debarre, O. and Fahlaoui, R., Abelian varieties in W dr(C) and points of bounded degree on algebraic curves, Compositio Math. 88 (1993), 235–249.Google Scholar
Evertse, J.-H., On sums of S-units and linear recurrences, Compositio Math. 53 (1984), 225–244.Google Scholar
Faltings, G., Diophantine approximation on abelian varieties, Ann. of Math. (2) 133 (1991), 549–576.CrossRefGoogle Scholar
Faltings, G., The general case of S. Lang’s conjecture, in Barsotti symposium in algebraic geometry (Abano Terme, 1991), Perspectives in Mathematics, vol. 15 (Academic Press, San Diego, CA, 1994), 175–182.CrossRefGoogle Scholar
Frey, G., Curves with infinitely many points of fixed degree, Israel J. Math. 85 (1994), 79–83.CrossRefGoogle Scholar
Harris, J. and Silverman, J. H., Bielliptic curves and symmetric products, Proc. Amer. Math. Soc. 112 (1991), 347–356.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., Diophantine geometry: an introduction, Graduate Texts in Mathematics, vol. 201 (Springer, New York, 2000).CrossRefGoogle Scholar
Kawamata, Y., On Bloch’s conjecture, Invent. Math. 57 (1980), 97–100.CrossRefGoogle Scholar
Lang, S., Fundamentals of Diophantine geometry (Springer, New York, 1983).CrossRefGoogle Scholar
Levin, A., Vojta’s inequality and rational and integral points of bounded degree on curves, Compositio Math. 143 (2007), 73–81.CrossRefGoogle Scholar
Levin, A., The dimensions of integral points and holomorphic curves on the complements of hyperplanes, Acta Arith. 134 (2008), 259–270.CrossRefGoogle Scholar
Levin, A., On the Zariski-density of integral points on a complement of hyperplanes in ℙn, J. Number Theory 128 (2008), 96–104.CrossRefGoogle Scholar
Levin, A., Generalizations of Siegel’s and Picard’s theorems, Ann. of Math. (2) 170 (2009), 609–655.CrossRefGoogle Scholar
Noguchi, J., Lemma on logarithmic derivatives and holomorphic curves in algebraic varieties, Nagoya Math. J. 83 (1981), 213–233.CrossRefGoogle Scholar
Noguchi, J., On holomorphic curves in semi-abelian varieties, Math. Z. 228 (1998), 713–721.CrossRefGoogle Scholar
Noguchi, J. and Ochiai, T., Geometric function theory in several complex variables, Mathematics Monographs, vol. 80 (American Mathematical Society, Providence, RI, 1990).CrossRefGoogle Scholar
Noguchi, J. and Winkelmann, J., Holomorphic curves and integral points off divisors, Math. Z. 239 (2002), 593–610.CrossRefGoogle Scholar
Noguchi, J. and Winkelmann, J., Nevanlinna theory in several complex variables and Diophantine approximation, Grundlehren der Mathematischen Wissenschaften, vol. 350 (Springer, Tokyo, 2014).CrossRefGoogle Scholar
Ochiai, T., On holomorphic curves in algebraic varieties with ample irregularity, Invent. Math. 43 (1977), 83–96.CrossRefGoogle Scholar
Siegel, C. L., Über einege Anwendungen Diophantischer Approximationen, Abh. Preuss. Akad. Wiss. Phys. Math. Kl. 1 (1929), 41–69.Google Scholar
Silverman, J. H., Arithmetic distance functions and height functions in Diophantine geometry, Math. Ann. 279 (1987), 193–216.CrossRefGoogle Scholar
Siu, Y.-T. and Yeung, S.-K., A generalized Bloch’s theorem and the hyperbolicity of the complement of an ample divisor in an abelian variety, Math. Ann. 306 (1996), 743–758.CrossRefGoogle Scholar
Stoll, W., Algebroid reduction of Nevanlinna theory, in Complex analysis, III (College Park, MD, 1985–1986), Lecture Notes in Mathematics, vol. 1277 (Springer, Berlin, 1987), 131–241.Google Scholar
van der Poorten, A. J. and Schlickewei, H. P., The growth condition for recurrence sequences, Macquarie University Math. Rep. 82-0041 (1982).Google Scholar
Vojta, P., Diophantine approximations and value distribution theory, Lecture Notes in Mathematics, vol. 1239 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Vojta, P., A generalization of theorems of Faltings and Thue–Siegel–Roth–Wirsing, J. Amer. Math. Soc. 5 (1992), 763–804.CrossRefGoogle Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. I, Invent. Math. 126 (1996), 133–181.CrossRefGoogle Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. II, Amer. J. Math. 121 (1999), 283–313.CrossRefGoogle Scholar

Altmetric attention score

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 108 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 28th February 2021. This data will be updated every 24 hours.

1 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Integral points of bounded degree on affine curves
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Integral points of bounded degree on affine curves
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Integral points of bounded degree on affine curves
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *