Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-26T14:11:50.473Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlation Functions, Universal Ratios and Goldstone Mode Singularities in n-Vector Models

Published online by Cambridge University Press:  03 June 2015

J. Kaupužs ,
R. V. N. Melnik  and
J. Rimšāns
J. Kaupužs*
Affiliation:
Institute of Mathematics and Computer Science, University of Latvia, 29 Raiņa Boulevard, LV1459, Riga, Latvia Institute of Mathematical Sciences and Information Technologies, University of Liepaja, 14 Liela Street, Liepaja LV-3401, Latvia
R. V. N. Melnik*
Affiliation:
Wilfrid Laurier University, Waterloo, Ontario, Canada, N2L 3C5
J. Rimšāns*
Affiliation:
Institute of Mathematics and Computer Science, University of Latvia, 29 Raiņa Boulevard, LV1459, Riga, Latvia Institute of Mathematical Sciences and Information Technologies, University of Liepaja, 14 Liela Street, Liepaja LV-3401, Latvia
*
Corresponding author.Email:kaupuzs@latnet.lv
Email:rmelnik@wlu.ca
Email:rimshans@mii.lu.lv
Get access

Abstract

Correlation functions in the 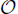(n) models below the critical temperature are considered. Based on Monte Carlo (MC) data, we confirm the fact stated earlier by Engels and Vogt, that the transverse two-plane correlation function of the 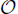(4) model for lattice sizes about L = 120 and small external fields h is very well described by a Gaussian approximation. However, we show that fits of not lower quality are provided by certain non-Gaussian approximation. We have also tested larger lattice sizes, up to L = 512. The Fourier-transformed transverse and longitudinal two-point correlation functions have Goldstone mode singularities in the thermodynamic limit at k → 0 and h = +0, i.e., G⊥ (k) ≃ ak–λ⊥ and G‖(k)≃bk–λ‖, respectively. Here a and b are the amplitudes, k = |k| is the magnitude of the wave vector k. The exponents λᚆ, λ‖ and the ratio bM2/a2, where M is the spontaneous magnetization, are universal according to the GFD (grouping of Feynman diagrams) approach. Here we find that the universality follows also from the standard (Gaussian) theory, yielding bM2/a2=(n−1)/16. Our MC estimates of this ratio are 0.06±0.01 for n=2, 0.17±0.01 for n = 4 and 0.498±0.010 for n = 10. According to these and our earlier MC results, the asymptotic behavior and Goldstone mode singularities are not exactly described by the standard theory. This is expected from the GFD theory. We have found appropriate analytic approximations for G⊥(k) and G‖(k), well fitting the simulation data for small k. We have used them to test the Patashinski-Pokrovski relation and have found that it holds approximately.

Keywords

65C0582B2082B80n-component vector modelscorrelation functionsMonte Carlo simulationGoldstone mode singularities
Type
Research Article
Information
Communications in Computational Physics , Volume 15 , Issue 5 , May 2014 , pp. 1407 - 1430
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Lawrie, I. D., Goldstone modes and coexistence in isotropic N-vector models, J. Phys. A, 14, 14 (1981), 2489–2502.CrossRefGoogle Scholar
[2]Lawrie, I. D., Goldstone mode singularities in specific heats and non-ordering susceptibilities of isotropic systems, J. Phys. A, 18 (1985), 1141–1152.Google Scholar
[3]Hasenfratz, P. and Leutwyler, H., Goldstone boson related finite size effects in field theory and critical phenomena with O(n) symmetry, Nucl. Phys., B343 (1990), 241–284.Google Scholar
[4]Täuber, U. C. and Schwabl, F., Critical dynamics of the O(n)-symmetric relaxational models below the transition temperature, Phys. Rev. B, 46 (1992), 3337–3361.Google Scholar
[5]Schäfer, L. and Horner, H., Goldstone mode singularities and equation of state of an isotropic magnet, Z. Phys. B, 29 (1978), 251.Google Scholar
[6]Anishetty, R., Basu, R., Hari, N. D. Dass and Sharatchandra, H. S., Infrared behaviour of systems with goldstone bosons, Int. J. Mod. Phys., A14 (1999), 3467–3496.Google Scholar
[7]Dupuis, N., Infrared behavior in systems with a broken continuous symmetry: classical O(N) model versus interacting bosons, Phys. Rev. E, 83 (2011), 031120.Google Scholar
[8]Brézin, E. and Wallace, D. J., Critical behavior of a classical heisenberg ferromagnet with many degrees of freedom, Phys. Rev. B, 7 (1973), 1967–1974.Google Scholar
[9]Wallace, D. J. and Zia, R. K., Singularities induced by Goldstone modes, Phys. Rev. B, 12 (1975), 5340–5342.CrossRefGoogle Scholar
[10]Nelson, D. R., Coexistence-curve singularities in isotropic ferromagnets, Phys. Rev. B, 13 (1976), 2222–2230.Google Scholar
[11]Brézin, E. and Zinn-Justin, J., Spontaneous breakdown of continuous symmetries near two dimensions, Phys. Rev. B, 14 (1976), 3110–3120.Google Scholar
[12]Dimitrović, I., Hasenfratz, P., Nager, J. and Niedermayer, F., Finite-size effects, goldstone bosons and critical exponents in the d=3 Heisenberg model, Nucl. Phys., B350 (1991), 893–950.Google Scholar
[13]Engels, J. and Mendes, T., Goldstone-mode effects and scaling function for the three-dimensional O(4) model, Nucl. Phys., B572 (2000), 289–304.CrossRefGoogle Scholar
[14]Engels, J., Holtman, S., Mendes, T. and Schulze, T., Equation of state and goldstone-mode effects of the three-dimensional O(2) model, Phys. Lett. B, 492 (2000), 219–227.Google Scholar
[15]Engels, J. and Vogt, O., Longitudinal and transverse spectral functions in the three-dimensional model, Nucl. Phys., B 832 (2010), 538–566.Google Scholar
[16]Kaupužs, J., Melnik, R. V. N. and Rimšāns, J., Advanced Monte Carlo study of the Goldstone mode singularity in the 3D XY model, Commun. Comput. Phys., 4 (2008), 124–134.Google Scholar
[17]Kaupuz, J.ˇs, Melnik, R. V. N. and Rimša¯ns, J., Monte Carlo estimation of transverse and longitudinal correlation functions in the O(4) model, Phys. Lett. A, 374 (2010), 1943–1950.Google Scholar
[18]Kaupuz, J.ˇs, Canadian Phys, J., 9 (2012), 373.Google Scholar
[19]Kaupužs, J., Melnik, R. V. N. and Rimša¯ns, J., Goldstone mode singularities in O(n) models, Condensed Matter Phys., 15 (2012), 43005.CrossRefGoogle Scholar
[20]Kaupužs, J., Longitudinal and transverse correlation functions in the ϕ 4 model below and near the critical point, Progress of Theoretical Phys., 124 (2010), 613–643.Google Scholar
[21]Kaupužs, J., Int. J. Mod. Phys., A27 (2012), 1250114.Google Scholar
[22]Dohm, V., Crossover from Goldstone to critical fluctuations: casimir forces in confined-symmetric systems, Rev. Lett., 110 (2013), 107207.Google Scholar
[23]Butera, P. and Comi, M., Critical specific heats of the N-vector spin models on the simple cubic and bcc lattices, Phys. Rev. B, 60 (1999), 6749–6760.CrossRefGoogle Scholar
[24]Ite, K. R. and Tamura, H., Commun. Math. Phys., 202 (1999), 127.Google Scholar
[25]Newman, M. E. J. and Barkema, G. T., Monte Carlo Methods in Statistical Physics, Clarendon Press, Oxford, 1999Google Scholar
[26]Erdélyi, A., Asymptotic representations of Fourier integrals and the method of stationary phase, J. Soc. Indust. Appl. Math., 3 (1955), 17–27.Google Scholar
[27]Fedoriuk, , Asymptotics Integrals and Series, Nauka, Moscow, 1987.Google Scholar
[28]Kötzler, J., Görlitz, D., Dombrowski, R. and Pieper, M., Z. Phys., B94 (1994), 9.CrossRefGoogle Scholar