Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mancini, Sara
Bernal, Francisco
and
Acebrón, Juan A.
2016.
An Efficient Algorithm for Accelerating Monte Carlo Approximations of the Solution to Boundary Value Problems.
Journal of Scientific Computing,
Vol. 66,
Issue. 2,
p.
577.
Bernal, Francisco
and
Acebrón, Juan A.
2016.
A multigrid-like algorithm for probabilistic domain decomposition.
Computers & Mathematics with Applications,
Vol. 72,
Issue. 7,
p.
1790.
BERNAL, FRANCISCO
DOS REIS, GONÇALO
and
SMITH, GREIG
2017.
Hybrid PDE solver for data-driven problems and modern branching.
European Journal of Applied Mathematics,
Vol. 28,
Issue. 6,
p.
949.
Bernal, Francisco
2019.
An Implementation of Milstein’s Method for General Bounded Diffusions.
Journal of Scientific Computing,
Vol. 79,
Issue. 2,
p.
867.
Milewski, Sławomir
2020.
A Matlab software for approximate solution of 2D elliptic problems by means of the meshless Monte Carlo random walk method.
Numerical Algorithms,
Vol. 83,
Issue. 2,
p.
565.
Hussain, Shah
Madi, Elissa Nadia
Khan, Hasib
Gulzar, Haseena
Etemad, Sina
Rezapour, Shahram
Kaabar, Mohammed K. A.
and
Avery, Richard I.
2022.
On the Stochastic Modeling of COVID-19 under the Environmental White Noise.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.
Koichubekov, Berik
Takuadina, Aliya
Korshukov, Ilya
Turmukhambetova, Anar
and
Sorokina, Marina
2023.
Is It Possible to Predict COVID-19? Stochastic System Dynamic Model of Infection Spread in Kazakhstan.
Healthcare,
Vol. 11,
Issue. 5,
p.
752.
Merle, Fabian
and
Prohl, Andreas
2023.
A posteriori error analysis and adaptivity for high-dimensional elliptic and parabolic boundary value problems.
Numerische Mathematik,
Vol. 153,
Issue. 4,
p.
827.
Bernal, Francisco
Morón-Vidal, Jorge
and
Acebrón, Juan A.
2023.
A hybrid probabilistic domain decomposition algorithm suited for very large-scale elliptic PDEs.
Computers & Mathematics with Applications,
Vol. 146,
Issue. ,
p.
294.
Koichubekov, Berik
Takuadina, Aliya
Korshukov, Ilya
Sorokina, Marina
and
Turmukhambetova, Anar
2023.
The Epidemiological and Economic Impact of COVID-19 in Kazakhstan: An Agent-Based Modeling.
Healthcare,
Vol. 11,
Issue. 22,
p.
2968.
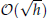 . We address specific implementation issues of the most
general-purpose of such schemes. They have been coded into a single Matlab program
and compared, according to their accuracy and computational cost, on a wide range of
problems in up to ℝ48. The paper is self-contained and the code will be
made freely downloadable.
. We address specific implementation issues of the most
general-purpose of such schemes. They have been coded into a single Matlab program
and compared, according to their accuracy and computational cost, on a wide range of
problems in up to ℝ48. The paper is self-contained and the code will be
made freely downloadable.



