Article contents
An Iterative Discontinuous Galerkin Method for Solving the Nonlinear Poisson Boltzmann Equation
Published online by Cambridge University Press: 03 June 2015
Abstract
An iterative discontinuous Galerkin (DG) method is proposed to solve the nonlinear Poisson Boltzmann (PB) equation. We first identify a function space in which the solution of the nonlinear PB equation is iteratively approximated through a series of linear PB equations, while an appropriate initial guess and a suitable iterative parameter are selected so that the solutions of linear PB equations are monotone within the identified solution space. For the spatial discretization we apply the direct discontinuous Galerkin method to those linear PB equations. More precisely, we use one initial guess when the Debye parameter λ = 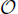 (1), and a special initial guess for λ ≫1 to ensure convergence. The iterative parameter is carefully chosen to guarantee the existence, uniqueness, and convergence of the iteration. In particular, iteration steps can be reduced for a variable iterative parameter. Both one and two-dimensional numerical results are carried out to demonstrate both accuracy and capacity of the iterative DG method for both cases of λ =
(1), and a special initial guess for λ ≫1 to ensure convergence. The iterative parameter is carefully chosen to guarantee the existence, uniqueness, and convergence of the iteration. In particular, iteration steps can be reduced for a variable iterative parameter. Both one and two-dimensional numerical results are carried out to demonstrate both accuracy and capacity of the iterative DG method for both cases of λ = 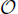 (1) and λ ≪ 1. The (m + 1)th order of accuracy for L2 and mth order of accuracy for H1 for Pm elements are numerically obtained.
(1) and λ ≪ 1. The (m + 1)th order of accuracy for L2 and mth order of accuracy for H1 for Pm elements are numerically obtained.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Global Science Press Limited 2014
References
- 5
- Cited by




