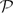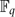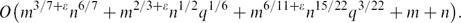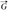Paper
Lazy Cops and Robbers on Hypercubes
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2015, pp. 829-837
-
- Article
- Export citation
Quantitative Equidistribution for Certain Quadruples in Quasi-Random Groups
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 376-381
-
- Article
- Export citation
Problem Papers
Set Systems Containing Many Maximal Chains
-
- Published online by Cambridge University Press:
- 09 October 2014, pp. 480-485
-
- Article
- Export citation
Introduction
Introduction
-
- Published online by Cambridge University Press:
- 26 May 2015, p. 584
-
- Article
- Export citation
Paper
Near Perfect Matchings in k-Uniform Hypergraphs
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 723-732
-
- Article
- Export citation
Formulae and Asymptotics for Coefficients of Algebraic Functions
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 1-53
-
- Article
- Export citation
Gaussian Distribution of Trie Depth for Strongly Tame Sources
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 54-103
-
- Article
- Export citation
Query Complexity of Sampling and Small Geometric Partitions
-
- Published online by Cambridge University Press:
- 21 October 2014, pp. 733-753
-
- Article
- Export citation
Optimal Codes in the Enomoto-Katona Space
-
- Published online by Cambridge University Press:
- 09 October 2014, pp. 382-406
-
- Article
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation
Problem Papers
A Binary Deletion Channel With a Fixed Number of Deletions
-
- Published online by Cambridge University Press:
- 07 October 2014, pp. 486-489
-
- Article
- Export citation
Paper
Sperner's Theorem and a Problem of Erdős, Katona and Kleitman
-
- Published online by Cambridge University Press:
- 01 December 2014, pp. 585-608
-
- Article
- Export citation
Decomposing Random Graphs into Few Cycles and Edges
- Part of:
-
- Published online by Cambridge University Press:
- 29 December 2014, pp. 857-872
-
- Article
- Export citation
The Sharp Threshold for Maximum-Size Sum-Free Subsets in Even-Order Abelian Groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 609-640
-
- Article
- Export citation
An Optimal Algorithm for Finding Frieze–Kannan Regular Partitions
-
- Published online by Cambridge University Press:
- 23 April 2014, pp. 407-437
-
- Article
- Export citation
Improved Bounds for Incidences Between Points and Circles
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 490-520
-
- Article
- Export citation
An Extension of the Hajnal–Szemerédi Theorem to Directed Graphs
-
- Published online by Cambridge University Press:
- 28 October 2014, pp. 754-773
-
- Article
- Export citation
Towards a Realistic Analysis of Some Popular Sorting Algorithms
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 104-144
-
- Article
- Export citation
On Directed Versions of the Hajnal–Szemerédi Theorem
-
- Published online by Cambridge University Press:
- 05 February 2015, pp. 873-928
-
- Article
- Export citation
On the Diameter of Random Planar Graphs
-
- Published online by Cambridge University Press:
- 18 September 2014, pp. 145-178
-
- Article
- Export citation