Article contents
Improved Bounds for Incidences Between Points and Circles
Published online by Cambridge University Press: 02 October 2014
Abstract
We establish an improved upper bound for the number of incidences between m points and n circles in three dimensions. The previous best known bound, originally established for the planar case and later extended to any dimension ≥ 2, is O*(m2/3n2/3 + m6/11n9/11 + m + n), where the O*(⋅) notation hides polylogarithmic factors. Since all the points and circles may lie on a common plane (or sphere), it is impossible to improve the bound in ℝ3 without first improving it in the plane.
Nevertheless, we show that if the set of circles is required to be ‘truly three-dimensional’ in the sense that no sphere or plane contains more than q of the circles, for some q ≪ n, then for any ϵ > 0 the bound can be improved to
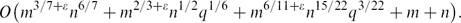 \[
O\bigl(m^{3/7+\eps}n^{6/7} + m^{2/3+\eps}n^{1/2}q^{1/6} + m^{6/11+\eps}n^{15/22}q^{3/22} + m + n\bigr).
\]
\[
O\bigl(m^{3/7+\eps}n^{6/7} + m^{2/3+\eps}n^{1/2}q^{1/6} + m^{6/11+\eps}n^{15/22}q^{3/22} + m + n\bigr).
\]
We present several extensions and applications of the new bound.
(i) For the special case where all the circles have the same radius, we obtain the improved bound O(m5/11+ϵn9/11 + m2/3+ϵn1/2q1/6 + m + n).
(ii) We present an improved analysis that removes the subpolynomial factors from the bound when m = O(n3/2−ϵ) for any fixed ϵ < 0.
(iii) We use our results to obtain the improved bound O(m15/7) for the number of mutually similar triangles determined by any set of m points in ℝ3.
Keywords
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2014
References
- 13
- Cited by


