Hostname: page-component-77c89778f8-rkxrd Total loading time: 0 Render date: 2024-07-16T22:05:21.231Z Has data issue: false hasContentIssue false
  • English
  • Français

Regions Without Complex Zeros for Chromatic Polynomials on Graphs with Bounded Degree

Published online by Cambridge University Press:  01 March 2008

ROBERTO FERNÁNDEZ  and
ALDO PROCACCI
ROBERTO FERNÁNDEZ
Affiliation:
Laboratoire de Mathématiques Raphaël Salem, UMR 6085 CNRS-Université de Rouen, Avenue de l'Université, BP.12, 76801 Saint Etienne du Rouvray, France (e-mail: Roberto.Fernandez@univ-rouen.fr)
ALDO PROCACCI
Affiliation:
Laboratoire de Mathématiques Raphaël Salem, UMR 6085 CNRS-Université de Rouen, Avenue de l'Université, BP.12, 76801 Saint Etienne du Rouvray, France (e-mail: Roberto.Fernandez@univ-rouen.fr) Departamento de Matemática-ICEx, UFMG, CP 702, Belo Horizonte MG 30.161-970, Brazil (e-mail: aldo@mat.ufmg.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

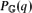We prove that the chromatic polynomial of a finite graph of maximal degree Δ is free of zeros for |q| ≥ C*(Δ) with 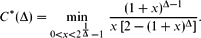This improves results by Sokal and Borgs. Furthermore, we present a strengthening of this condition for graphs with no triangle-free vertices.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 2 , March 2008 , pp. 225 - 238
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Borgs, C. (2006) Absence of zeros for the chromatic polynomial on bounded degree graphs. Combin. Probab. Comput. 15 63–74.CrossRefGoogle Scholar
[2]Brydges, D. C. (1984) A short cluster in cluster expansions. In Critical Phenomena, Random Systems, Gauge Theories (Osterwalder, K. and Stora, R., eds), Elsevier, pp. 129–83.Google Scholar
[3]Cammarota, C. (1982) Decay of correlations for infinite range interactions in unbounded spin systems. Comm. Math. Phys. 85 517–28.CrossRefGoogle Scholar
[4]Dobrushin, R. L. (1996) Estimates of semi-invariants for the Ising model at low temperatures. In Topics in Statistics and Theoretical Physics. Amer. Math. Soc. Transl. Ser. 2 177 59–81.Google Scholar
[5]Gruber, C. and Kunz, H. (1971) General properties of polymer systems. Comm. Math. Phys. 22 133–61.CrossRefGoogle Scholar
[6]Fernández, R. and Procacci, A. (2007) Cluster expansions for abstract polymer models: New bounds from an old approach. Preprint arXiv math-ph/0605041; Comm. Math. Phys. 274 123–40.Google Scholar
[7]Kotecký, R. and Preiss, D. (1986) Cluster expansion for abstract polymer models. Comm. Math. Phys. 103 491–498.CrossRefGoogle Scholar
[8]Penrose, O. (1967) Convergence of fugacity expansions for classical systems. In Statistical Mechanics: Foundations and Applications (Bak, A., ed.), Benjamin, New York.Google Scholar
[9]Procacci, A. and Scoppola, B. (1999) Polymer gas approach to N-body lattice systems. J. Statist. Phys. 96 49–68.CrossRefGoogle Scholar
[10]Procacci, A., Scoppola, B. and Gerasimov, V. (2003) Potts model on infinite graphs and the limit of chromatic polynomials. Comm. Math. Phys. 235 215–31.CrossRefGoogle Scholar
[11]Ruelle, D. (1969) Statistical Mechanics: Rigorous Results, Benjamin, New York/Amsterdam.Google Scholar
[12]Sokal, A. (2001) Bounds on the complex zeros of (di)chromatic polynomials and Potts-model partition functions. Combin. Probab. Comput. 10 41–77.CrossRefGoogle Scholar