Article contents
Near-perfect clique-factors in sparse pseudorandom graphs
Published online by Cambridge University Press: 11 December 2020
Abstract
We prove that, for any 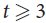 $t \ge 3$, there exists a constant c = c(t) > 0 such that any d-regular n-vertex graph with the second largest eigenvalue in absolute value λ satisfying
$t \ge 3$, there exists a constant c = c(t) > 0 such that any d-regular n-vertex graph with the second largest eigenvalue in absolute value λ satisfying 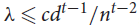 $\lambda \le c{d^{t - 1}}/{n^{t - 2}}$ contains vertex-disjoint copies of kt covering all but at most
$\lambda \le c{d^{t - 1}}/{n^{t - 2}}$ contains vertex-disjoint copies of kt covering all but at most 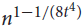 ${n^{1 - 1/(8{t^4})}}$ vertices. This provides further support for the conjecture of Krivelevich, Sudakov and Szábo (Combinatorica24 (2004), pp. 403–426) that (n, d, λ)-graphs with n ∈ 3ℕ and
${n^{1 - 1/(8{t^4})}}$ vertices. This provides further support for the conjecture of Krivelevich, Sudakov and Szábo (Combinatorica24 (2004), pp. 403–426) that (n, d, λ)-graphs with n ∈ 3ℕ and 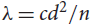 $\lambda \le c{d^2}/n$ for a suitably small absolute constant c > 0 contain triangle-factors. Our arguments combine tools from linear programming with probabilistic techniques, and apply them in a certain weighted setting. We expect this method will be applicable to other problems in the field.
$\lambda \le c{d^2}/n$ for a suitably small absolute constant c > 0 contain triangle-factors. Our arguments combine tools from linear programming with probabilistic techniques, and apply them in a certain weighted setting. We expect this method will be applicable to other problems in the field.
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
JH was supported by FAPESP (2014/18641-5, 2013/03447-6).
YK was partially supported by CNPq (311412/2018-1, 423833/2018-9) and FAPESP (2018/04876-1).
YP was supported by DFG grant PE 2299/1-1.
The cooperation of the authors was supported by a joint CAPES-DAAD PROBRAL project (project 430/15, 57350402, 57391197). This research was partially supported by CAPES (Finance Code 001). FAPESP is the São Paulo Research Foundation. CNPq is the National Council for Scientific and Technological Development of Brazil.
References
- 2
- Cited by





