Article contents
Generalizations of the Ruzsa–Szemerédi and rainbow Turán problems for cliques
Published online by Cambridge University Press: 19 November 2020
Abstract
Considering a natural generalization of the Ruzsa–Szemerédi problem, we prove that for any fixed positive integers r, s with r < s, there are graphs on n vertices containing 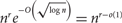 $n^{r}e^{-O\left(\sqrt{\log{n}}\right)}=n^{r-o(1)}$
copies of Ks such that any Kr is contained in at most one Ks. We also give bounds for the generalized rainbow Turán problem ex (n, H, rainbow - F) when F is complete. In particular, we answer a question of Gerbner, Mészáros, Methuku and Palmer, showing that there are properly edge-coloured graphs on n vertices with
$n^{r}e^{-O\left(\sqrt{\log{n}}\right)}=n^{r-o(1)}$
copies of Ks such that any Kr is contained in at most one Ks. We also give bounds for the generalized rainbow Turán problem ex (n, H, rainbow - F) when F is complete. In particular, we answer a question of Gerbner, Mészáros, Methuku and Palmer, showing that there are properly edge-coloured graphs on n vertices with 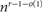 $n^{r-1-o(1)}$
copies of Kr such that no Kr is rainbow.
$n^{r-1-o(1)}$
copies of Kr such that no Kr is rainbow.
MSC classification
- Type
- Paper
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 4
- Cited by





