Article contents
Forward Clusters for Degenerate Random Environments
Published online by Cambridge University Press: 24 May 2016
Abstract
We consider connectivity properties and asymptotic slopes for certain random directed graphs on ℤ2 in which the set of points 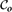 $\mathcal{C}_o$ that the origin connects to is always infinite. We obtain conditions under which the complement of
$\mathcal{C}_o$ that the origin connects to is always infinite. We obtain conditions under which the complement of 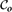 $\mathcal{C}_o$ has no infinite connected component. Applying these results to one of the most interesting such models leads to an improved lower bound for the critical occupation probability for oriented site percolation on the triangular lattice in two dimensions.
$\mathcal{C}_o$ has no infinite connected component. Applying these results to one of the most interesting such models leads to an improved lower bound for the critical occupation probability for oriented site percolation on the triangular lattice in two dimensions.
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2016
References
- 4
- Cited by




