Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-05T09:10:13.190Z Has data issue: false hasContentIssue false
  • English
  • Français

Diameters in Supercritical Random Graphs Via First Passage Percolation

Published online by Cambridge University Press:  05 October 2010

JIAN DING ,
JEONG HAN KIM ,
EYAL LUBETZKY  and
YUVAL PERES
JIAN DING
Affiliation:
Department of Statistics, UC Berkeley, Berkeley, CA 94720, USA (e-mail: jding@stat.berkeley.edu)
JEONG HAN KIM
Affiliation:
Department of Mathematics, Yonsei University, Seoul 120-749, Korea and National Institute for Mathematical Sciences, Daejeon 305-340, Korea (e-mail: jehkim@yonsei.ac.kr)
EYAL LUBETZKY
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052-6399, USA (e-mail: eyal@microsoft.com, peres@microsoft.com)
YUVAL PERES
Affiliation:
Microsoft Research, One Microsoft Way, Redmond, WA 98052-6399, USA (e-mail: eyal@microsoft.com, peres@microsoft.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the diameter of 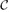1, the largest component of the Erdős–Rényi random graph 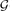(n, p) in the emerging supercritical phase, i.e., for p = 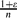where ε3n → ∞ and ε = o(1). This parameter was extensively studied for fixed ε > 0, yet results for ε = o(1) outside the critical window were only obtained very recently. Prior to this work, Riordan and Wormald gave precise estimates on the diameter; however, these did not cover the entire supercritical regime (namely, when ε3n → ∞ arbitrarily slowly). Łuczak and Seierstad estimated its order throughout this regime, yet their upper and lower bounds differed by a factor of .

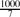We show that throughout the emerging supercritical phase, i.e., for any ε = o(1) with ε3n → ∞, the diameter of 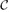1 is with high probability asymptotic to D(ε, n) = (3/ε)log(ε3n). This constitutes the first proof of the asymptotics of the diameter valid throughout this phase. The proof relies on a recent structure result for the supercritical giant component, which reduces the problem of estimating distances between its vertices to the study of passage times in first-passage percolation. The main advantage of our method is its flexibility. It also implies that in the emerging supercritical phase the diameter of the 2-core of 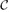1 is w.h.p. asymptotic to 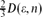, and the maximal distance in 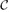1 between any pair of kernel vertices is w.h.p. asymptotic to .

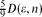Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 729 - 751
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Addario-Berry, L., Broutin, N. and Goldschmidt, C. (2009) The continuum limit of critical random graphs. Available at: http://arxiv.org/abs/0903.4730.Google Scholar
[2]Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, 3rd edn, Wiley-Interscience Series in Discrete Mathematics and Optimization.CrossRefGoogle Scholar
[3]Bandelt, H.-J. and Chepoi, V. (2008) Metric graph theory and geometry: A survey. In Surveys on Discrete and Computational Geometry, Vol. 453 of Contemporary Mathematics, AMS, Providence, RI, pp. 49–86.Google Scholar
[4]Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2010) First passage percolation on random graphs with finite mean degrees. Ann. Appl. Probab. 20 1907–1965.CrossRefGoogle Scholar
[5]Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. Europ. J. Combin. 1 311–316.Google Scholar
[6]Bollobás, B. (2001) Random Graphs, 2nd edn, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
[7]Bollobás, B. (1984) The evolution of random graphs. Trans. Amer. Math. Soc. 286 257–274.Google Scholar
[8]Bollobás, B., Janson, S. and Riordan, O. (2007) The phase transition in inhomogeneous random graphs. Random Struct. Alg. 31 3–122.CrossRefGoogle Scholar
[9]Chung, F. and Lu, L. (2001) The diameter of sparse random graphs. Adv. Appl. Math. 26 257–279.Google Scholar
[10]Ding, J., Kim, J. H., Lubetzky, E. and Peres, Y. Anatomy of a young giant component in the random graph. Random Struct. Alg., in press. Available at: http://arxiv.org/abs/0906.1839.Google Scholar
[11]Erdős, P. and Rényi, A. (1959) On random graphs I. Publ. Math. Debrecen 6 290–297.Google Scholar
[12]Fernholz, D. and Ramachandran, V. (2007) The diameter of sparse random graphs. Random Struct. Alg. 31 482–516.Google Scholar
[13]Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization.CrossRefGoogle Scholar
[14]Kesten, H. (1986) Aspects of first passage percolation. In École d'Été de Probabilités de Saint-Flour, XIV, 1984, Vol. 1180 of Lecture Notes in Mathematics, Springer, pp. 125–264.CrossRefGoogle Scholar
[15]Łuczak, T. (1990) Component behavior near the critical point of the random graph process. Random Struct. Alg. 1 287–310.CrossRefGoogle Scholar
[16]Łuczak, T. (1998) Random trees and random graphs. Random Struct. Alg. (Proc. Eighth International Conference ‘Random Structures and Algorithms’, Poznan 1997) 13 485–500.3.0.CO;2-Y>CrossRefGoogle Scholar
[17]Łuczak, T. and Seierstad, T. G. The diameter behavior in the random graph process. Preprint.Google Scholar
[18]Lyons, Russell (1992) Random walks, capacity and percolation on trees. Ann. Probab. 20 2043–2088.Google Scholar
[19]Nachmias, A. and Peres, Y. (2008) Critical random graphs: Diameter and mixing time. Ann. Probab. 36 1267–1286.Google Scholar
[20]Peres, Y. (1997) Probability on trees: An introductory climb. In Lectures on Probability Theory and Statistics (Saint-Flour), Vol. 1717 of Lecture Notes in Mathematics, Springer, pp. 193–280.Google Scholar
[21]Riordan, O. and Wormald, N. C. (2008) The diameter of sparse random graphs. Preprint, available at: http://arxiv.org/abs/0808.4067v1.Google Scholar
[22]Riordan, O. and Wormald, N. C. (2009) The diameter of sparse random graphs. To appear, available at: http://arxiv.org/abs/0808.4067v2.Google Scholar
[23]Wormald, N. C. (1999) Models of random regular graphs. In Surveys in Combinatorics 1999, Vol. 267 of London Mathematical Society Lecture Notes, Cambridge University Press, pp. 239–298.Google Scholar