Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-27T23:55:45.328Z Has data issue: false hasContentIssue false
  • English
  • Français

A blurred view of Van der Waerden type theorems

Part of: Extremal combinatorics Sequences and sets

Published online by Cambridge University Press:  26 November 2021

Vojtech Rödl  and
Marcelo Sales Open the ORCID record for Marcelo Sales [Opens in a new window]
Vojtech Rödl
Affiliation:
Department of Mathematics, Emory University, Atlanta, GA 30322, USA
Marcelo Sales*
Affiliation:
Department of Mathematics, Emory University, Atlanta, GA 30322, USA
*
*Corresponding author. Email: mtsales@emory.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 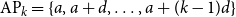$\mathrm{AP}_k=\{a,a+d,\ldots,a+(k-1)d\}$ be an arithmetic progression. For 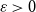$\varepsilon>0$ we call a set 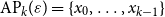$\mathrm{AP}_k(\varepsilon)=\{x_0,\ldots,x_{k-1}\}$ an $\varepsilon$ -approximate arithmetic progression if for some a and d, 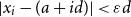$|x_i-(a+id)|<\varepsilon d$ holds for all 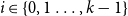$i\in\{0,1\ldots,k-1\}$ . Complementing earlier results of Dumitrescu (2011, J. Comput. Geom.2(1) 16–29), in this paper we study numerical aspects of Van der Waerden, Szemerédi and Furstenberg–Katznelson like results in which arithmetic progressions and their higher dimensional extensions are replaced by their $\varepsilon$ -approximation.

Keywords

CombinatoricsArithmetic progressionsRamsey theory

MSC classification

Primary: 05D10: Ramsey theory
Secondary: 11B25: Arithmetic progressions
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 4 , July 2022 , pp. 684 - 701
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Ronald Graham

The first author was supported by NSF grant DMS 1764385.

The second author was partially supported by NSF grant DMS 1764385.

References

Behrend, F. A. (1946) On sets of integers which contain no three terms in arithmetical progression. Proc. Nat. Acad. Sci. USA 32 331–332.CrossRefGoogle Scholar
Berlekamp, E. R. (1968) A construction for partitions which avoid long arithmetic progressions. Canad. Math. Bull. 11 409–414.CrossRefGoogle Scholar
Brown, T. C., Graham, R. L. and Landman, B. M. (1999) On the set of common differences in van der Waerden’s theorem on arithmetic progressions. Canad. Math. Bull. 42(1) 25–36.CrossRefGoogle Scholar
Dumitrescu, A. (2011) Approximate Euclidean Ramsey theorems. J. Comput. Geom. 2(1) 16–29.Google Scholar
Elkin, M. (2011) An improved construction of progression-free sets. Israel J. Math. 184 93–128.CrossRefGoogle Scholar
Erdös, P. and Graham, R. L. (1980) Old and new problems and results in combinatorial number theory: van der Waerden’s theorem and related topics. Enseign. Math. (2) 25(3–4) 325–344.Google Scholar
Erdös, P. and Turán, P. (1936) On some sequences of integers. J. London Math. Soc. 11(4) 261–264.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y. (1978) An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34 275–291 (1979).CrossRefGoogle Scholar
Furstenberg, H. (1977) Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 204–256.CrossRefGoogle Scholar
Gowers, W. T. (2001) A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11(3) 465–588.CrossRefGoogle Scholar
Gowers, W. T. (2007) Hypergraph regularity and the multidimensional Szemerédi theorem. Ann. Math. (2) 166(3) 897–946.CrossRefGoogle Scholar
Graham, R. L. and Nešetřil, J. (1986) Large minimal sets which force long arithmetic progressions. J. Combin. Theory Ser. A 42(2) 270–276.CrossRefGoogle Scholar
Graham, R. (2006) On the growth of a van der Waerden-like function. Integers 6, A29, 5.Google Scholar
Graham, R. (2008) Old and new problems and results in Ramsey theory. In Horizons of Combinatorics, pp. 105–118.CrossRefGoogle Scholar
Green, B. and Wolf, J. (2008) A note on elkin’s improvement of behrend’s constructions, arXiv:0810.0732, 4 p. 14Google Scholar
Han, J., Kohayakawa, Y., Sales, M. T. and Stagni, H. (2019) On some extremal results for order types. Acta Math. Univ. Comenian. (N.S.) 88(3) 779–785.Google Scholar
Han, J., Kohayakawa, Y., Sales, M. T. and Stagni, H. (2019) Extremal and probabilistic results for order types. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 426–435.CrossRefGoogle Scholar
Laba, I. and Lacey, M. T. (2001) On sets of integers not containing long arithmetic progressions, arXiv:math, 8, p. 14Google Scholar
Moshkovitz, G. and Shapira, A. (2019) A tight bound for hyperaph regularity. Geom. Funct. Anal. 29(5) 1531–1578.CrossRefGoogle Scholar
Nagle, B., Rodl, V. and Schacht, M. (2006) The counting lemma for regular k-uniform hypergraphs. Random Struct. Algorithms 28(2) 113–179.CrossRefGoogle Scholar
O’Bryant, K. (2011) Sets of integers that do not contain long arithmetic progressions. Electron. J. Combin. 18(1), Paper 59, 15.Google Scholar
Rankin, R. A. Sets of integers containing not more than a given number of terms in arithmetical progression. Proc. R. Soc. Edinburgh Sect. A 65(1960/61) 332–344 (1960/61).CrossRefGoogle Scholar
Rodl, V. and Skokan, J. (2004) Regularity lemma for k-uniform hypergraphs. Random Struct. Algorithms 25(1) 1–42.CrossRefGoogle Scholar
Rosser, J. B. and Schoenfeld, L. (1975) Sharper bounds for the Chebyshev functions $\theta(x)$ and $\psi(x)$ . Math. Comp. 29 243–269.Google Scholar
Szabo, Z. (1990) An application of Lovasz’ local lemma|a new lower bound for the van der Waerden number. Random Struct. Algorithms 1(3) 343–360.CrossRefGoogle Scholar