Article contents
Large complete minors in random subgraphs
Published online by Cambridge University Press: 03 December 2020
Abstract
Let G be a graph of minimum degree at least k and let Gp be the random subgraph of G obtained by keeping each edge independently with probability p. We are interested in the size of the largest complete minor that Gp contains when p = (1 + ε)/k with ε > 0. We show that with high probability Gp contains a complete minor of order 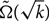 $\tilde{\Omega}(\sqrt{k})$
, where the ~ hides a polylogarithmic factor. Furthermore, in the case where the order of G is also bounded above by a constant multiple of k, we show that this polylogarithmic term can be removed, giving a tight bound.
$\tilde{\Omega}(\sqrt{k})$
, where the ~ hides a polylogarithmic factor. Furthermore, in the case where the order of G is also bounded above by a constant multiple of k, we show that this polylogarithmic term can be removed, giving a tight bound.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Supported by the Austrian Science Fund (FWF): I3747.
Supported in part by USA–Israel BSF grant 2018267, and by ISF grant 1261/17.
References
- 2
- Cited by





