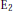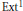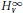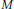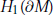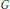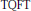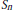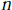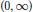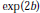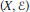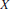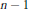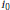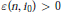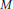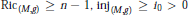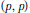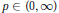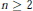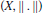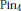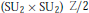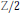Research Article
Hecke Operations and the Adams E2-Term Based on Elliptic Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-138
-
- Article
-
- You have access
- Export citation
Essential Norm and Weak Compactness of Composition Operators on Weighted Banach Spaces of Analytic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-148
-
- Article
-
- You have access
- Export citation
A Note on Finite Dehn Fillings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-154
-
- Article
-
- You have access
- Export citation
Non Cohen-Macaulay Vector Invariants and a Noether Bound for a Gorenstein Ring of Invariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 155-161
-
- Article
-
- You have access
- Export citation
Lorentz-Schatten Classes and Pointwise Domination of Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 162-168
-
- Article
-
- You have access
- Export citation
Heat Kernels of Lorentz Cones
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 169-173
-
- Article
-
- You have access
- Export citation
Rings With Comparability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-183
-
- Article
-
- You have access
- Export citation
On Arithmetic Means of Sequences Generated by a Periodic Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-189
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
Topological Quantum Field Theory and Strong Shift Equivalence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-197
-
- Article
-
- You have access
- Export citation
Research Article
Commutators and Analytic Dependence of Fourier-Bessel Series on (0, ∞)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-208
-
- Article
-
- You have access
- Export citation
Ample Vector Bundles of Curve Genus One
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-213
-
- Article
-
- You have access
- Export citation
Conjugate Radius and Sphere Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 214-220
-
- Article
-
- You have access
- Export citation
Boundedness of the q-Mean-Square Operator on Vector-Valued Analytic Martingales
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 221-230
-
- Article
-
- You have access
- Export citation
Generating Ideals in Rings of Integer-Valued Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-236
-
- Article
-
- You have access
- Export citation
On Benson’s Definition of Area in Minkowski Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 237-247
-
- Article
-
- You have access
- Export citation
The Classification of Pin4-Bundles over a 4-Complex
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 248-256
-
- Article
-
- You have access
- Export citation