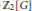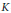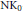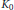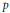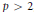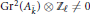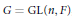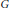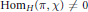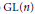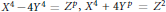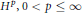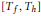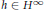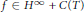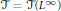Research Article
Sur les singularités de la fonction croissance d’une variété non simplement connexe
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-167
-
- Article
-
- You have access
- Export citation
Biquadratic Extensions with One Break
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 168-179
-
- Article
-
- You have access
- Export citation
On the Exponent of the NK0-Groups of Virtually Infinite Cyclic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 180-195
-
- Article
-
- You have access
- Export citation
Mahler Measures Close to an Integer
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-203
-
- Article
-
- You have access
- Export citation
On the Chow Groups of Supersingular Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 204-212
-
- Article
-
- You have access
- Export citation
Griffiths Groups of Supersingular Abelian Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 213-219
-
- Article
-
- You have access
- Export citation
Globalization of Distinguished Supercuspidal Representations of GL(n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 220-230
-
- Article
-
- You have access
- Export citation
Correction
Erratum: The Lehmer Polynomial and Pretzel Links
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 231
-
- Article
-
- You have access
- Export citation
Research Article
On Strongly Convex Indicatrices in Minkowski Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 232-246
-
- Article
-
- You have access
- Export citation
On a Few Diophantine Equations Related to Fermat’s Last Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 247-256
-
- Article
-
- You have access
- Export citation
Modular Forms Associated to Theta Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-264
-
- Article
-
- You have access
- Export citation
On the Smirnov Class Defined by the Maximal Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-271
-
- Article
-
- You have access
- Export citation
The Transfer in the Invariant Theory of Modular Permutation Representations II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-282
-
- Article
-
- You have access
- Export citation
Residue: A Geometric Construction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-293
-
- Article
-
- You have access
- Export citation
Modular Subgroups, Forms, Curves and Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 294-308
-
- Article
-
- You have access
- Export citation
Joint Mean Oscillation and Local Ideals in the Toeplitz Algebra II: Local Commutivity and Essential Commutant
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 309-318
-
- Article
-
- You have access
- Export citation