Research Article
Solutions with Singular Initial Data for a Model of Electrophoretic Separation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
-
- Article
-
- You have access
- Export citation
Sur les Sous-Groupes Purifiables des Groupes Abéliens Primaires
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-17
-
- Article
-
- You have access
- Export citation
Families of Sequences of 0s and 1s In FK-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 18-23
-
- Article
-
- You have access
- Export citation
Dependent Random Variables with Independent Subsets - II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-28
-
- Article
-
- You have access
- Export citation
A Note on Hardy-Orlicz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-33
-
- Article
-
- You have access
- Export citation
Exponential Estimates for the Conjugate Function on Locally Compact Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 34-44
-
- Article
-
- You have access
- Export citation
A Banach Space in Which a Ball is Contained in the Range of Some Countably Additive Measure is Superreflexive
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-49
-
- Article
-
- You have access
- Export citation
On Coefficients of Artin L Functions as Dirichlet Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-54
-
- Article
-
- You have access
- Export citation
Limit Cycles Close to Infinity of Certain Non-Linear Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-59
-
- Article
-
- You have access
- Export citation
On the Spectrum of the Bergman-Hilbert Matrix II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-64
-
- Article
-
- You have access
- Export citation
Pseudoumbilical 2-Type Surfaces in Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-68
-
- Article
-
- You have access
- Export citation
Ring Derivations on Function Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-72
-
- Article
-
- You have access
- Export citation
Some Special Conjugacy Closed Loops
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 73-78
-
- Article
-
- You have access
- Export citation
Factors of Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-83
-
- Article
-
- You have access
- Export citation
A Simple Proof for the Unicity of the Limit Cycle in the Bogdanov-Takens System
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 84-92
-
- Article
-
- You have access
- Export citation
Extensions that are Submodules of their Quotients
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 93-99
-
- Article
-
- You have access
- Export citation
Sur les Fonctions Analytiques Multiformes dont les Valeurs Sont des Segments
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-105
-
- Article
-
- You have access
- Export citation
Unruly Hilbert Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-109
-
- Article
-
- You have access
- Export citation
Ends of spaces related by a covering map
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 110-118
-
- Article
-
- You have access
- Export citation
Half-Silvered Mirrors and Wythoff's Game
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-125
-
- Article
-
- You have access
- Export citation

 )
)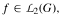 the conjugate function of
the conjugate function of 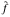 whose Fourier transform satisfies the identity
whose Fourier transform satisfies the identity 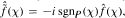 for almost all
for almost all 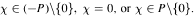 We prove that, when
We prove that, when 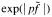 is integrable for all
is integrable for all