Research Article
Projective Orthomodular Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-153
-
- Article
-
- You have access
- Export citation
The Average Edge Order of 3-Manifold Coloured Triangulations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 154-161
-
- Article
-
- You have access
- Export citation
A Note on Quotient Fields of Power Series Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 162-164
-
- Article
-
- You have access
- Export citation
Weak Amenability of Group Algebras of Locally Compact Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 165-167
-
- Article
-
- You have access
- Export citation
Small Sets of k-th Powers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 168-173
-
- Article
-
- You have access
- Export citation
On a Property of Nilpotent Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-177
-
- Article
-
- You have access
- Export citation
Nonoscillation of Second Order Superlinear Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 178-186
-
- Article
-
- You have access
- Export citation
Weighted Occupation Time for Branching Particle Systems and a Representation for the Supercritical Superprocess
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 187-196
-
- Article
-
- You have access
- Export citation
A Singular Integral on L2(Rn)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-201
-
- Article
-
- You have access
- Export citation
Trace Classes and Quadratic Forms in the Modular Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-212
-
- Article
-
- You have access
- Export citation
Imaginary Verma Modules for Affine Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 213-218
-
- Article
-
- You have access
- Export citation
Atomless Lattice-Ordered Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 219-221
-
- Article
-
- You have access
- Export citation
The Macneille Completion of a Uniquely Complemented Lattice
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-227
-
- Article
-
- You have access
- Export citation
Units of Integral Group Rings of Some Metacyclic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 228-237
-
- Article
-
- You have access
- Export citation
On a Characterization of Real Hypersurfaces of Type a in a Complex Space Form
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 238-244
-
- Article
-
- You have access
- Export citation
Isotropic Immersions into a Real Space Form
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 245-253
-
- Article
-
- You have access
- Export citation
Self-Affine Processes and the Ergodic Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 254-262
-
- Article
-
- You have access
- Export citation
Geometric Proofs of some Classical Results on Boundary Values for Analytic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-269
-
- Article
-
- You have access
- Export citation
Measures Below Outer Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-271
-
- Article
-
- You have access
- Export citation
One Sided SF-Rings with Certain Chain Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-277
-
- Article
-
- You have access
- Export citation

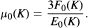
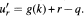 Then for every ε > 0 and
Then for every ε > 0 and 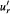
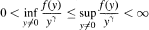
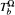 associated to a kernel
associated to a kernel 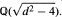 The algorithm mentioned above then provides a new straightforward computational procedure for determining
The algorithm mentioned above then provides a new straightforward computational procedure for determining 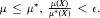 Thus there is a non-zero outer (finitely subadditive) measure
Thus there is a non-zero outer (finitely subadditive) measure