Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-28T10:54:45.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeros of Linear Combinations of Polynomials

Published online by Cambridge University Press:  20 November 2018

Q. I. Rahman
Q. I. Rahman*
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following theorem is due to J. L. Walsh (see [2, Theorem 17, 2a]):

Theorem. If all the zeros of f1(z)=zn+a1zn-1+ … + an lie in or on the circle C1 with centre c1 and radius r1 and if all the zeros of f2(z)=zn+b1zn-1+ … + bn lie in or on the circle C2 with centre c2 and radius r2, then each zero of the polynomial

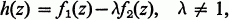
lies in at least one of the circles Γk with centre γk and radius ρk, where

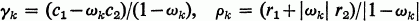
and where the ωk (k= 1, 2,…, n) are the nth roots of λ.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 1 , March 1972 , pp. 139 - 142
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Dieudonné, J., Sur quelques propriétés des polynômes. Actualités Sci. Indust. No. 114, Hermann, Paris, 1934.Google Scholar
2. Marden, M., Geometry of polynomials, Math. Surveys No. 3, Amer. Math. Soc, Providence, R.I., 1966.Google Scholar