Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-20T08:25:10.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Semiprojectivity for Purely Infinite C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Jack Spielberg
Jack Spielberg*
Affiliation:
Department of Mathematics and Statistics, Arizona State University, Tempe, AZ 85287-1804, U.S.A.. e-mail: jack.spielberg@asu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that a separable, nuclear, purely infinite, simple ${{C}^{*}}$-algebra satisfying the universal coefficient theorem is weakly semiprojective if and only if its 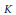$K$-groups are direct sums of cyclic groups.

Keywords

46L0522A2246L80Kirchberg algebraweak semiprojectivitygraphC*-algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 3 , 01 September 2007 , pp. 460 - 468
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Blackadar, B., Shape theory for C*-algebras. Math. Scand. 56(1985), no. 2, 249–275.Google Scholar
[2] Blackadar, B., Semiprojectivity in simple C*-algebras. In: Operator Algebras and Applications. Adv. Stud. Pure Math. 38 Mathematical Society of Japan, Tokyo, 2004, pp. 1–17,Google Scholar
[3] Effros, E. G. and Kaminker, J., Homotopy continuity and shape theory for C*-algebras. In: Geometric Methods in Operator Algebras. Pitman Research Notes in Mathematics Series 123, Longman Scientific and Technical, Harlow, 1986.Google Scholar
[4] Eilers, S. and Loring, T., Computing contingencies for stable relations. Internat. J. Math. 10(1999), no. 3, 301–326.Google Scholar
[5] Kaplansky, I., Infinite Abelian Groups. revised edition. University of Michigan Press, Ann Arbor, MI, 1969.Google Scholar
[6] Kumjian, A. and Pask, D., Higher rank graph C*-algebras. New York J. Math. 6(2000), 1–20 (electronic).Google Scholar
[7] Lin, H.,Weak semiprojectivity in purely infinite simple C*-algebras. Canad. J. Math. 59(2007), no. 2, 343–371.Google Scholar
[8] Loring, T., Lifting Solutions to Perturbing Problems in C*-algebras. Fields Institute Monographs 8, American Mathematical Society, Providence, RI, 1997.Google Scholar
[9] Neubüser, B., Semiprojektivität und realisierunen von rein unendlichen C*-algebren. http://wwwmath1.uni-muenster.de/sfb/about/publ/neubueser01.html Google Scholar
[10] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5(2000), 49–114 (electronic).Google Scholar
[11] Rørdam, M., Classification of nuclear C*-algebras. In: Classification of Nuclear C*-Algebras. Entropy in Operator Algebras. Encyclopaedia Math. Sci. 126, Springer, Berlin, 2002.Google Scholar
[12] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55(1987), no. 2, 431–474.Google Scholar
[13] Spielberg, J., A functorial approach to the C*-algebras of a graph. Internat. J. Math. 13(2002), no. 3, 245–277.Google Scholar
[14] Spielberg, J., Semiprojectivity for certain purely infinite C*-algebras. To appear, Trans. Amer. Math. Soc.Google Scholar
[15] Spielberg, J., Graph-based models for Kirchberg algebras. To appear, J. Operator Theory.Google Scholar
[16] Spielberg, J., Non-cyclotomic presentations of modules and prime-order automorphisms of Kirchberg algebras. To appear, J. Reine Angew. Math.Google Scholar
[17] Szymański, W., On semiprojectivity of C*-algebras of directed graphs. Proc. Amer. Math. Soc. 130(2002), no. 5, 1391–1399.Google Scholar
[18] Zhang, S., Certain C*-algebras with real rank zero and their corona and multiplier algebras. I. Pacific J. Math. 155(1992), no. 1, 169–197.Google Scholar