Hostname: page-component-84b7d79bbc-g5fl4 Total loading time: 0 Render date: 2024-07-28T10:07:18.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Von Neumann Operators in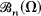

Published online by Cambridge University Press:  20 November 2018

Karim Seddighi
Karim Seddighi*
Affiliation:
Pennsylvania State UniversityUniversity Park, Pennsylvania16802
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a connected open subset Ω of the plane and n a positive integer, let 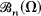be the space introduced by Cowen and Douglas in their paper, “Complex geometry and operator theory”. Our main concern is the case n = 1, in which case we show the existence of a functional calculus for von Neumann operators in 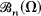for which a spectral mapping theorem holds. In particular we prove that if the spectrum of 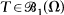, is a spectral set for T, and if 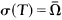, then σ(f(T)) = f(Ω)- for every bounded analytic function f on the interior of L, where L is compact, σ(T) ⊂ L, the interior of L is simply connected and L is minimal with respect to these properties. This functional calculus turns out to be nice in the sense that the general study of von Neumann operators in 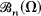is reduced to the special situation where Ω is an open connected subset of the unit disc 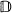with .

Keywords

47B2047A6047B3747A2Von Neumann operatorfunctional calculusspectral setspectral mapping
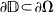Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 2 , 01 June 1984 , pp. 146 - 156
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Agler, J., An invariant subspace theorem, J. Functional analysis, 38 (1980), 315–323.Google Scholar
2. Conway, J., Functions of One Complex Variable, Springer Verlag, Inc., New York (1973).Google Scholar
3. Conway, J., Subnormal Operators, Pitman Publishing Co., London (1981).Google Scholar
4. Conway, J. and Olin, R., A functional calculus for subnormal operators, II Memoirs A.M.S., Vol. 184.Google Scholar
5. Cowen, M. and Douglas, R., Complex geometry and operator theory, Acta Math., 141 (1978), 187–261.Google Scholar
6. Dixmier, J., Les algèbres d’operateurs dans Vespace hilbertien, Gauthier-Villars, Paris, 1957.Google Scholar
7. Gamelin, T., Uniform Algebras, Prentice Hall, Englewood Cliffs, New Jersey, 1969.Google Scholar
8. Gamelin, T. and Garnett, J., Pointwise bounded approximation and hypodirichlet algebras, Bull. Amer. Math. Soc, 77 (1971), 137–141.Google Scholar
9. Halmos, P., A Hilbert Space Problem Book, Van Nostrand Co., Princeton, New Jersey, 1967.Google Scholar
10. Rudin, W., Functional Analysis, McGraw-Hill, New York, 1973.Google Scholar
11. Sarason, D., Weak-star density of polynomials, J. fur Reine Angew. Math, 252 (1972), 1–15.Google Scholar