Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-27T12:55:51.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Very Ample Linear Systems on Blowings-Up at General Points of Projective Spaces

Published online by Cambridge University Press:  20 November 2018

Marc Coppens
Marc Coppens*
Affiliation:
Katholieke Hogeschool Kempen Departement Industrieel Ingenieur en Biotechniek Campus H. I. Kempen Kleinhoefstraat 4 B 2440 Geel Belgium, e-mail: marc.coppens@khk.be
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 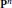${{\mathbf{P}}^{n}}$ be the $n$-dimensional projective space over some algebraically closed field $k$ of characteristic 0. For an integer 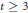$t\,\ge \,3$ consider the invertible sheaf 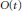$O\left( t \right)$ on 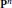${{\mathbf{P}}^{n}}$ (Serre twist of the structure sheaf). Let 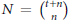$N\,=\,\left( \underset{n}{\mathop{t+n}}\, \right)$, the dimension of the space of global sections of 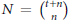$O\left( t \right)$, and let $k$ be an integer satisfying 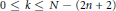$0\,\le \,k\,\le \,N\,-\,\left( 2n\,+\,2 \right)$. Let 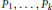${{P}_{1}},\ldots ,{{P}_{k}}$ be general points on 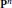${{\mathbf{P}}^{n}}$ and let 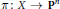$\pi :\,X\,\to \,{{\mathbf{P}}^{n}}$ be the blowing-up of 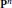${{\mathbf{P}}^{n}}$ at those points. Let 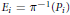${{E}_{i}}\,=\,{{\pi }^{-1}}\left( {{P}_{i}} \right)$ with 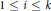$1\,\le \,i\,\le \,k$ be the exceptional divisor. Then 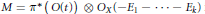$M={{\pi }^{*}}\left( O(t) \right)\,\otimes \,{{O}_{X}}\left( -{{E}_{1}}-\cdots -{{E}_{k}} \right)$ is a very ample invertible sheaf on 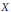$X$.

Keywords

14E2514N0514N15blowing-upprojective spacevery ample linear systemembeddingsVeronese map
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 3 , 01 September 2002 , pp. 349 - 354
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Biancofiore, A., On the hyperplane sections of ruled surfaces. Lecture Notes in Math. 1417 (1988), 1417–1988.Google Scholar
[2] Chauvin, S. and De Volder, C., Some very ample and base point free linear systems on generic rational surfaces. Preprint, 2000.Google Scholar
[3] Coppens, M., Embeddings of general blowing-ups at points. J. Reine Angew.Math. 469 (1995), 469–1995.Google Scholar
[4] Coppens, M., Very ample linear systems on blowings-up at general points of smooth projective varieties. Pacific J. Math., to appear.Google Scholar
[5] d'Almeida, J. and Hirschowitz, A., Quelques plongements non-spéciaux de surfaces rationelles. Math. Z. 211 (1992), 211–1992.Google Scholar
[6] De Volder, C., Very ampliness and Gauss maps of linear systems on blowings-up of projective varieties. Ph.D. thesis, Gent, 2000.Google Scholar
[7] Sernesi, E., Topics on families of projective schemes. Queen's Papers in Pure and Appl. Math. 73(1986), Queen's University, Kingston, Ontario.Google Scholar
[8] Szemberg, T. and Tutaj-Gasinska, H., Embeddings of general blowups of abelian surfaces. Manuscripta Math., to appear.Google Scholar
[9] Szemberg, T. and Tutaj-Gasinska, H., General blowups of ruled surfaces. Preprint, 2000.Google Scholar