Article contents
Value Sets of Sparse Polynomials
Published online by Cambridge University Press: 24 September 2019
Abstract
We obtain a new lower bound on the size of the value set 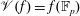 $\mathscr{V}(f)=f(\mathbb{F}_{p})$ of a sparse polynomial
$\mathscr{V}(f)=f(\mathbb{F}_{p})$ of a sparse polynomial 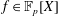 $f\in \mathbb{F}_{p}[X]$ over a finite field of
$f\in \mathbb{F}_{p}[X]$ over a finite field of 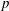 $p$ elements when
$p$ elements when 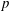 $p$ is prime. This bound is uniform with respect to the degree and depends on some natural arithmetic properties of the degrees of the monomial terms of
$p$ is prime. This bound is uniform with respect to the degree and depends on some natural arithmetic properties of the degrees of the monomial terms of 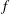 $f$ and the number of these terms. Our result is stronger than those that can be extracted from the bounds on multiplicities of individual values in
$f$ and the number of these terms. Our result is stronger than those that can be extracted from the bounds on multiplicities of individual values in 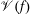 $\mathscr{V}(f)$.
$\mathscr{V}(f)$.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
Author I. E. S. was supported by ARC Grants DP170100786 and DP180100201.
References
- 2
- Cited by




